基于虚拟标量场的WSNs 融合中心选址方法*

顾 德，王继帅

(1.江南大学 自动化研究所，轻工过程先进控制教育部重点实验室，江苏 无锡214122;2.中国科学院 苏州生物医学工程技术研究所，江苏 苏州215163)

0 引 言

无线传感器网络(wireless sensor networks，WSNs)常用于收集某一特定区域内的信息，将信息汇总到数据融合中心之后与互联网相连。因此，数据融合中心是WSNs 的核心［1，2］，在一个特定的应用中数据融合中心的数量和位置对整个网络能否达到预期的性能表现有着极为重要的影响。

WSNs 部署区域的几何形状对网络自组织、路由、信息处理等过程有着深刻影响，瓶颈将导致工作负荷不均衡部分节点能耗过高和信道拥塞延迟加剧等问题［3，4］。如果能将WSNs 部署区域分割成若干凸的子区域，在每个子区域的中心放置一个数据融合中心，就能廻避由几何形状带来的问题。

如果能获取整个网络中所有节点的位置信息对完成上述任务极为有利。然而，WSNs 本身的特点决定了很难创造出这样的有利条件。首先，索求全局信息能量和时间代价很高;其次，绝对定位系统(如GPS)会增加WSNs 节点的成本和能耗，而相对定位目前也仍然是WSNs 的研究话题。

本文的研究就是在每个WSNs 节点都只拥有本身和相邻节点的局部信息并且不需要位置信息的限制下，试图将一个复杂形状的WSNs 部署区域进行近凸分割，并寻找到分割后的每个子区域的中心位置放置数据融合中心。

Zhu X J 等人［5］在相似的假设和限制下提出了一种分割算法，但此算法需要完美的边界识别结果为前提，并且在某些情况下，完全相同的节点部署，只交换节点ID 排序，就导致分割结果完全不同。尽管存在以上不足，该论文对本文算法思想的形成起到了启发作用。

1 算法思想的来源

本文所提出的算法受到一次对热传导现象观察的启发:一个不规则外形的各向同性的均匀高温(TH)固体被放入大量充分搅拌的冷水中(假设冷水的温度始终保持不变)。最初，固体表面迅速降温到冷水的温度(TL)，内部仍然保持高温;由于热传导作用，固体内部逐渐降温;最终，整个固体降温到冷水温度。

在温度逐渐变化的过程，记点P(x，y，z)在时间t 的温度是T(x，y，z，t)。给定时间t，则温度场的梯度为

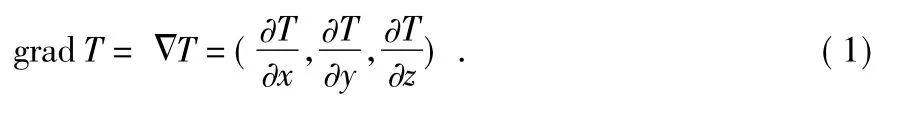
温度梯度与等温面垂直并指向高温处。傅立叶定律指出

其中，q 为热通量，λ 为导热系数。记固体的密度为ρ，比热容为c，导热系数为λ，根据式(1)和式(2)，可求点P(x，y，z)随时间t 变化的规律

热固体降温过程中，以下性质值得注意:

1)由于存在确定的初始条件(固体内部温度均为TH)和固定边界条件(整个过程中固表面始终保持TL)，式(3)对于任何P 和任何t 有定解，即可以获得在任意时间的温度分布，如图1 所示。

图1 某时刻温度场分布(深色表示高温)Fig 1 Distribution of temperature field at one time(darker color indicates hight temperature)

2)热传导需要媒质，只要获取P(x，y，z)邻域内点的温度信息就能计算P 的温度变化。

3)由于固体表面是最低温TL的等温面，温度梯度线都指向内部，并均将终止于极大值点。

4)汇聚到不同极大值点的温度梯度线将整个温度场分割成若干近凸分块。

5)这些极大值点都接近分块的中心位置。

以上性质分别说明:温度分布的变化可以通过数学计算模拟，模拟过程中只需要获得邻域内的温度分布;温度梯度线可以帮助完成区域分割;分块中心可由极大值点找到。

2 网络融合中心选址方法

2.1 确定WSNs 边界

首先，应当选择Wang Y［6］，Saukh O［7］或顾德［8］在其论文中提出的算法确定WSNs 的边界。处在边界上的点的虚拟温度始终固定在TL，其他点的虚拟温度赋予初值TH，其中TH＞TL。

2.2 模拟热传导过程

将传感器节点视为固体块中的一个微小子块，用节点间的单跳通信关系模拟固体中微小子块间的相邻关系。假设某个节点bi与n 个其他节点相邻，记节点bi的虚拟温度值为Ti，其相邻节点b1，b2，…，bn的虚拟温度值分别为T1，T2，…，Tn。将式(3)在空间上离散化可得

进一步在时间上离散化可得

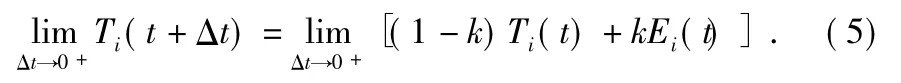
完成若干次迭代之后，在整个WSNs 中就建立了虚拟温度场。

2.3 虚拟梯度线和极大值

在上文中建立的虚拟离散温度场中，设Tj=max(T1，T2，…，Tn，Ti)，若i≠j，则bj是bi的邻节点中虚拟温度值最大的节点是由bi指向bj的梯度线;若i=j，则bi是虚拟温度的局部极大值点。

2.4 完成WSNs 部署区域的分割和融合中心选址

如果将梯度线视为节点间唯一存在的拓扑关系，那么，整个网络就成为若干以虚拟温度极大值节点为根节点树形网络。这些树形网络把原有的复杂形状的WSNs 分割成若干近凸分块，并且树的根节点接近整个分块中心，可以选择作为融合中心放置的位置。与K-means 算法［9］(取k=5，并拥有全局节点位置信息)求得的最优解相比，5 个根节点距离最优解的平均距离是单跳通信距离的0.21 倍，已接近数据融合中心的最优选址。

图2 演示了整个算法过程，在(a)～(g)中用Z 轴表示虚拟温度值，折线表示温度梯度线。(a)为最初阶段;(b)～(g)非边界节点根据式(6)迭代，最终获得如(g)中所示的结果;(g)在水平面上的投影如(h)所示，整个网络被分割成若干拓扑树，完成了近凸分块，并且根节点均处于接近所在分块中心的位置。(g)，(h)图中，两个不同拓扑树的交界位置用圆点标出。

2.5 算法复杂度分析

以下分析从确定WSNs 边界开始，直至算法完成的复杂度。

图2 算法运行过程示意，图中的线段表示虚拟温度梯度线Fig 2 Operation process of algorithm，lines in this demo represent gradients of virtual temperature

对于一个特定的节点，用式(6)模拟热传导的过程中，每个节点需要的完成O(n)次通信，耗时为O(1)，其中，n为平均节点密度(即平均每个节点拥有的邻节点数量)。根据虚拟温度梯度寻找拓扑树的父节点的过程，每个节点需要的完成O(n)次通信，耗时为O(1)。拓扑树的根节点将其身份信息传递到属于该树的所有节点的过程，每个节点需要完成至多O(n)次通信，耗时为O(1)。

以上所有过程中，节点需要获取和存储的信息仅限于邻节点的ID 和当前的虚拟温度值，所以，需要的存储空间为O(n)。

综上，为了本文所提出的算法，每个节点总共需要耗费的通信次数为O(n)，耗时为O(1)，需占用的存储空间为O(n)。由于遍历邻节点不可避免，所以，在复杂度的数量级上已没有继续优化的可能。

3 仿真与分析

3.1 边界识别部分缺失的影响

图2(h)是在边界完整的条件下获得的结果，但是边界识别问题目前还无法满足这一要求。

图3 所示的算例中，节点分布情况与图2(h)完全相同，但随机地将边界节点中的一部分设定为非边界节点。图3(a)是边界漏认60%时的结果，与图2(h)相差不大;图3(b)，(c)，分别是边界漏认65%和70%时的结果，分块数量增多，树的根节点位置明显偏离分块中心。对不同比例的边界漏认分别做20 次实验，把出现形如图3(b)，(c)的分块错误的次数记录下来，得到图4。

图3 不完整边界的影响Fig 3 Impact of imperfect boundary

图4 分块错误与边界漏认的关系Fig 4 Relationship between block error and boundary missing

分析以上仿真结果，当漏认率较低时，被漏认的边界节点零散地出现;漏认逐渐增多，边界节点连续漏认的概率缓慢增高，当超过某个临界值时，漏认节点形成连续的漏认链条的概率急剧增加，在漏认链条的中点附近就会出现一个局部极大值点，导致分块错误。由于临界值高达60%左右，可认为本算法对于边界漏认有足够容忍度，能够应对边界识别不完整。

3.2 节点部署密度的影响

在第2 节有“均匀”和“各向同性”的假设。当节点部署很密集时，这两个假设基本成立;如果密度下降，则将背离这两个假设，后面的分析和设计就有可能不正确。

图2(h)的平均节点密度是10.2，逐渐降低部署的节点数量。图5(a)所示的算例平均密度为8.1;(b)所示的算例平均密度为6.4，该密度下部分算例出现多余分块，拓扑树的根节点也明显偏离分块的中心;(c)所示的算例平均密度为4.4，几乎所有算例都出现分块错误，拓扑树根节点也经常不在节点中心。

图5 部署密度的影响Fig 5 Impact of deployment density

设大量算例中5%的算例出现错误的平均密度为密度临界值，那么仿真实验表明:密度临界值在7.1～8.0 之间。

3.3 各种不同的形状

将本文提出的算法应用到各种不同形状的WSNs 中，则获得了如图6 结果，平均节点密度均在10 左右，融合中心选址与利用全局信息求得的最优选址的距离如表1 所示。

从表1 中可以发现，各算例中的根节点与最优选址之间的平均距离都不到单跳通信距离。这说明本算法中各个根节点可作为网络融合中心的选址。

图6 各种不同形状WSNs 融合中心的选址结果Fig 6 Fusion center positioning result of different shapes WSNs

表1 各算例根节点距离最优选址的平均距离(以单跳通信距离的倍数计)Tab 1 Average distance of the optimal positions of each example rootnodes(counts by multiple of communication distance of single hop)

4 结 论

本文受热传导现象的启发，在WSNs 中模拟热传导的过程，通过观察某时刻的温度场合温度梯度，对复杂形状的WSNs 进行近凸分割，并找到各分块的中心。

通过仿真实验，考察了本算法对于不完整边界识别、低密度网络以及各种几何形状的容忍程度，验证了算法的适应性和实用性。

［1］ Karl H，Willig A.Protocols and architectures for wireless sensor networks［M］.Hoboken:John Wiley＆Sons，2007.

［2］ Akyildiz I F，Kasimoglu I H.Wireless Sensor and actor networks:Research challenges［J］.Ad Hoc Networks，2004，2(4):351－367.

［3］ Shin K，Lee H，Cho D-H.Diba:Distributed bottleneck alleviation scheme in wireless multi-hop sensor networks［J］.IEEE Communications Letters，2014，18(3):431－434.

［4］ Gou H，Yoo Y.Distributed bottleneck node detection in wireless sensor networks［C］∥IEEE 10th International Conference on Computer and Information Technology(CIT)，2010:218－224.

［5］ Zhu X J，Sarkar R，Gao J.Segmenting a sensor field:Algorithms and applications in network design［J］.ACM Transactions on Sensor Networks(TOSN)，2009，5(2):1－32.

［6］ Wang Y，Gao J，Mitchell J S B.Boundary recognition in sensor networks by topological methods［C］∥Proceedings of the 12th Annual International Conference on Mobile Computing and Networking，2006:122－133.

［7］ Saukh O，Sauter R，Gauger M，et al.On boundary recognition without location information in wireless sensor networks［J］.ACM Transactions on Sensor Networks(TOSN)，2010，6(3):1－35.

［8］ 顾 德，王继帅.无线传感器网络拓扑边界辨识算法［J］.传感器与微系统，2015，34(6):123－125.

［9］ MacQueen J B.Some methods for classification and analysis of multivariate observations［C］∥Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability，1967:281－297.