基于粒子群优化算法的无传感器调速系统研究*

杨圣蓉，王剑平，王 思，张 果，杨晓洪

(昆明理工大学 信息工程与自动化学院，云南 昆明650500)

0 引 言

永磁同步电机(PMSM)因具有高功率密度、高效率、高可靠性等优良性能，被广泛应用于各种性能要求高的场合。对PMSM 的直接控制(如矢量控制和直接转矩控制)［1］中需要安装传感器来采集电机的转速和转子位置信号，带来的问题是传感器的安装、测量准确性以及误差都会影响控制系统的可靠性。为解决上述问题而提出的无传感器技术［2］已经成为近年来的研究热点，其中，基于卡尔曼的估计方法以其良好的动态性和鲁棒性而备受关注［3，4］。

卡尔曼滤波器(Kalman filter，KF)自1960 年被提出［5］，已成为控制、信号处理与通信等领域最基本最重要的计算方法和工具之一，并被成功应用到航空、航天、工业过程及社会经济等不同领域［5～6］。扩展卡尔曼滤波(EKF)观测器由于不受电压直流偏移量的影响，可有效抑制噪声，而且具有良好的低速性能，对电机参数的变化较为敏感，在电机控制中得到了广泛应用。

EKF 中噪声协方差矩阵的选取会直接影响系统的性能，研究者们对此问题也进行了很多尝试，如Shi K L 等人［7］使用遗传算法优化协方差矩阵，文献［8］采用自适应KF 来实现噪声协方差矩阵自适应变化，文献［9］中采用模拟退火法优化EKF。本文采用粒子群优化(PSO)算法优化EKF，并利用优化得到的EKF 观测PMSM 的转速。

PSO 是Kenndy J 等人［10］受人工生命研究结果的启发而提出的一种基于群体智能的全局随机搜索算法，它基于“种群”和“进化”的概念，通过群体中每个个体的合作和竞争，实现复杂空间最优解的搜索。

为了解决EKF 中噪声协方差阵对估计准确性影响较大，且选取较困难的问题，设计了基于STM32的PMSM调速系统，利用PSO 算法离线选取和优化EKF 的噪声协方差阵，并利用该系统对电机进行了实时性能测试分析。实验结果表明:使用PSO 算法优化EKF 的PMSM 调速系统能解决EKF 中噪声协方差阵选取困难的问题，且系统的估计准确性较高。

1 基于EKF 的PMSM 观测器模型

EKF 过程实际上是一个循环迭代过程，循环由时间更新方程和状态更新方程构成

1)时间更新方程

2)状态更新方程

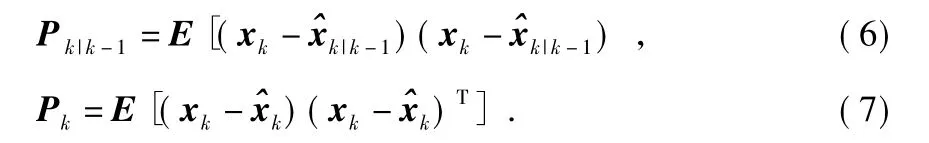
其中，Fk，k－1为状态转移矩阵;Hk为观测矩阵;Kk为滤波增益阵;Q 为系统噪声的协方差矩阵，R 为观测噪声的协方差矩阵。

为了使用EKF 同时观测负载转矩和电机状态，将负载转矩增广为状态变量，可得到PMSM 的状态方程

其中，ud/uq为定子电压d/q 轴分量，id/iq为定子电流d/q 轴分量，Ls为定子电感，Rs为定子电阻，ψf为永磁体磁链，ωe为转子电角速度，θe为转子位置角，Np为电机极对数，J 为转动惯量。

选取状态变量为x=［idiqωeθeTL］，输入变量u=［uduq］T，观测变量y=［idiq］T，得到基于EKF 的PMSM 观测器矩阵如下

2 PSO 算法

如图1，PSO 算法首先在可行解空间中初始化一群粒子，每个粒子都代表着问题的一个潜在最优解，且每个粒子对应一个适应度值。设粒子群规模为N，每个粒子在D 维空间中运动，组成的粒子群X=［X1，X2，…，XN］，其中，第i个粒子在D 维空间中的位置Xi=［Xi1，Xi2，…，XiD］T，当前的速度Vi=［Vi1，Vi2，…，ViD］T。在每次迭代过程中，粒子通过个体极值Pi和群体极值Pg来更新自身的速度和位置，标准的PSO 算法可描述为［11］

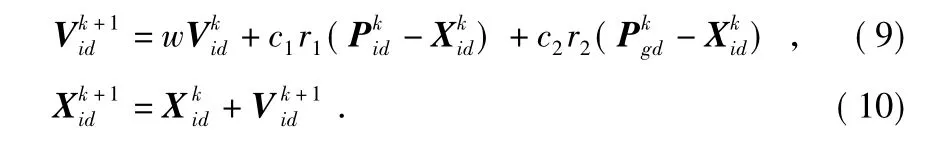
其中，w 为惯性权重，d=1，2，…，N;k 为当前迭代次数;Vid为粒子的速度;c1，c2为加速度因子;r1和r2为分布于［0，1］区间相互独立的随机数。

惯性权重w 的加入可以防止粒子飞出问题空间而发生群体“爆炸”现象，体现的是粒子继承先前速度的能力。Shi Y［12］最先将惯性权重引入PSO 算法中，并分析指出较大的惯性权值有利于全局搜索，较小的惯性权值更利于局部搜索，且w 不变的粒子群易陷入局部最优，求解精度低。为了更好地平衡算法的全局，文中采用线性递减惯性权重(linear decreasing inertia weight，LDIW)，如式(11)所示，这种动态w 值可以增强算法在后期的局部搜索能力，利于算法跳出局部最优解而求得最优解，提高算法的求解精度

式中 wstart为初始惯性权重，wend为迭代至最大次数时的惯性权重，k 为当前迭代次数，Tmax为最大迭代次数。

选取使用给定转速和电机输出转速的均方差误差(root-mean-square error，RMSE)作为评价系统性能的指标，其定义如下

式中 s 为给定转速，e 为电机实际输出转速，n 为采样次数。

图1 PSO 算法流程图Fig 1 Flow chart of PSO algorithm

3 实 验

选取PMSM 的参数为:额定转速nN=3 000 r/min，定子电阻Rs=2.1 Ω;定子电感Ls=1.4 mH;极对数Np=4。系统采用智能IPM 模块实现主电路的功率变换功能，以STM32F407ZET6 作为核心控制器组成控制电路，使用PSO离线优化噪声协方差阵，建立无速度传感器矢量控制系统，并使用Keil 软件编程并进行实时调试。将电机检测到的转速数据通过串口实时传送到所设计的界面。

3.1 硬件设计

本文所设计的无传感器调速系统的硬件主要由主回路和控制回路构成。主回路有整流模块、滤波电路、智能功率模块IPM 和PMSM 组成。控制回路包括主控芯片STM32F407ZET6、定子电流检测电路、直流侧母线电压检测电路等。控制系统硬件结构如图2 所示。

图2 控制系统硬件结构图Fig 2 Hardware structure of control system

系统主控芯片STM32F407ZET6 拥有Cortex M4 内核，负责处理采样得到的母线电压、定子电流等信号，然后通过EKF 算法得到六路PWM 控制信号，经光耦隔离和驱动放大等处理之后控制逆变器的开关状态。STM32F407ZET6还监控系统的运行状态，当系统出现短路、过流、过压、欠压以及过热等故障时，及时封锁PWM 输出信号，使电机停机。

3.2 软件设计

在Keil 平台上进行程序开发，程序主要由主程序和中断服务程序组成。主程序完成系统各个模块的初始化，包括CPU 时钟初始化、I/O 端口初始化、中断向量表初始化、设置定时器、A/D 转换初始化、片内寄存器初始化等。A/D转换、矢量控制、SVPWM、EKF 控制程序用中断服务程序实现。由于PSO 算法计算量大，STM32F407 尚不能进行处理，选择离线选取和优化卡尔曼滤波器中的矩阵参数，主要的中断服务程序流程图如图3 所示。

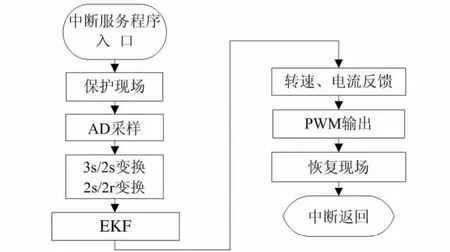
图3 中断服务程序流程图Fig 3 Flow chart of interrupt service program

3.3 实验结果

为了实时直观监控电机的运行，采用Qt 设计上位机界面，通过串口实时采集转速信号并在上位机显示。给定转速为nN=1 000 r/min 得到的转速波形如图4 所示。

图4 转速波形Fig 4 Rotating speed waveform

图4 的曲线分别表示给定转速和实时检测到的电机转子端输出转速，由图可知，转速能较快达到给定，且几乎无超调。可见设计的控制系统性能较优，得到的EKF 观测器能对转速进行精确的估计，PSO 离线得到的参数也较满意。

4 结 论

本文研究了基于PSO的EKF观测器估计PMSM转速的方法，使用PSO 离线选取和优化EKF 所需要的协方差阵，解决了EKF 噪声协方差阵选取较困难的问题。利用STM32 控制器搭建系统进行实验，实验结果表明:所设计的控制系统能满足控制性能、快速实时跟随给定，实现无传感器精确控制。

［1］ Hafeez M，Uddin M Nasir，Rahim Nasrudin Abd，et al.Self-tuned NFC and adaptive torque hysteresis-based DTC scheme for IN drive［J］.IEEE Transactions on Industry Applications，2014，50(2):1410－1419.

［2］ Yin Zhanggang，Zhao Chang，Liu Jing，et al.Research on antierror performance of speed and flux estimator for induction motor using robust reduced-order EKF［J］.IEEE Transactions on Industrial Informatics，2013，9(2):1037－1046.

［3］ 王宏健，王 晶，边信黔，等.基于组合EKF 的自主水下航行器SLAM［J］.机器人，2012，34(1):56－64.

［4］ Alonge Francesco，D’Ippolito Filippo，Sferlazza Antonini.Sensorless control of induction-motor drive based on robust Kalman filter and adaptive speed estimation［J］.IEEE Transactions on Industrial Electronic，2014，61(3):1444－1453.

［5］ Kalman R.A new approach to linear filtering and prediction problems［J］.Trans ASME，J Basic Eng，1960，82D:35－45.

［6］ 沈 悦，张 雷，傅忠谦，等.区间卡尔曼滤波算法在高动态导航的研究［J］.宇航学报，2013，34(37):355－361.

［7］ Shi K L，Chan T F，Wong Y K，et al.Speed estimation of an induction motor drive using an optimized extended Kalman filter［J］.IEEE Trans Ind Electron，2002，49(1):124－133.

［8］ 余洪霞，胡静涛.基于自适应卡尔曼滤波的异步电机转速和负载转矩估计［J］.数据采集与处理，2012，27(5): 522－558.

［9］ Buyamin S，Finch J W.Comparative study on optimising the EKF for speed estimation of an induction motor using simulated annealing and genetic algorithm［C］∥2007 IEEE International Electric Machines and Drives Conference，2007:1689－1694.

［10］Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proceedings of the 4th IEEE International Conference on Neural Networks，Piscataway:IEEE Service Center，1995:1942－1948.

［11］史 峰，王 辉，郁 磊，等.Matlab 智能算法30 个案例分析［M］.北京:北京航空航天大学出版社，2011.

［12］Shi Y，Eberhart R.Empirical study of particle swarm optimization［C］∥Proc IEEE Congr Evol Comput，1999:1945－1950.