HHT 在动态称重传感器处理非线性信号中的应用

刘玉龙，李晓林

(太原理工大学 信息工程学院，山西 太原030000)

0 引 言

动态称重(weight in motion，WIM)是指车辆在运动状态下经过称重设备从而得到车辆的重量。称重传感器是动态称重系统的核心构件，极大地影响着称重系统的精度。相比静态称重而言，动态称重效率更高，更适合现在节奏更快的物流运输检测需求，但是静态称重时是车辆平稳的静止在称重设备上，除了车辆自身没有其他干扰，所以，更容易得到精确的重量值。但是动态称重过程中就会面临多种影响，比如:路面状况;车辆荷载状态;称重设备使用年限过多;车辆行驶状态等［1］。在各种影响因素的作用下，致使传统的信号分析方法对于称重过程中的非线性、非平稳信号解析的不够精确，这就直接影响到了动态称重系统的精度。由于汽车振动干扰是低频信号，而轴重信号也是低频信号，因此，用简单的滤波方法不能有效去除各种低频干扰［2］。

本文引入希尔伯特—黄变换(HHT)信号处理方法来力求更加精确地解析出称重传感器接收到的非线性信号，得到更加真实的称重数据，从而得到更加准确的重量值。

1 悬臂梁称重传感器

目前，车辆动态称重系统均采用轴载计量方式，即通过称量汽车每个轴的重量，最终得到该车辆的总重。称重传感器一般由2 组安装在秤台两边固定架的悬臂梁称重传感器构成(如图1 所示)，安装时一端固定在秤台上，另一端通过压头加载秤台承受的重量，内部采用钢球传力结构，具有良好的密封性能。受力后能自动调心，具有安装简单、使用方便、互换性好等优点，车辆经过时即可根据传感器电压信号的变化来得到车辆的真实轴重。

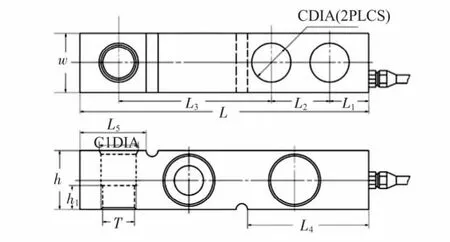
图1 悬臂梁称重传感器Fig 1 Cantilever beam weighing sensor

动态称重系统如图2 所示。

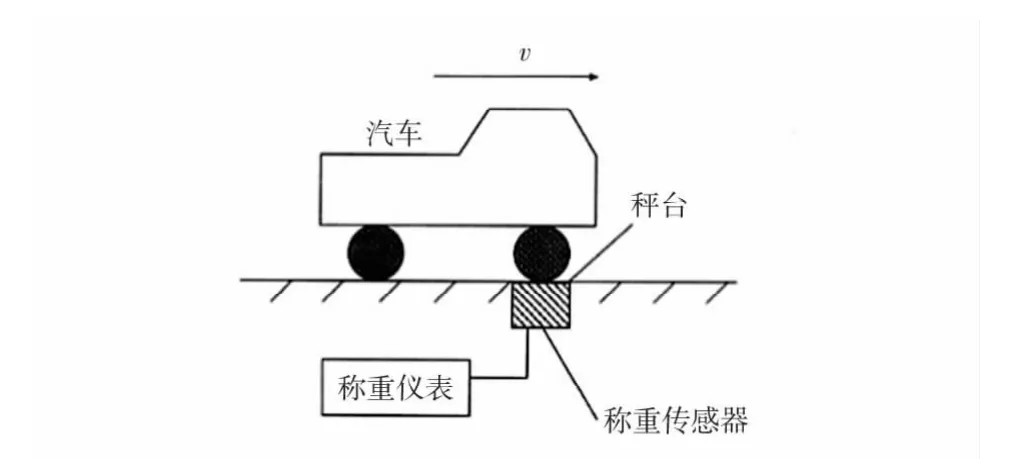
图2 动态称重系统示意图Fig 2 Diagram of WIM system

就目前的动态称重设备而言，一般称重平均误差均在±5%～±30%不等，相应的置信度为90%～95%［3］。目前，动态称重系统对于称重信号的处理一般采用以下几种:积分法、滤波法、参数估计以及神经网络［4，5］。传统的信号处理方法最终都是建立在傅里叶分析的基础上［6］，但是由于傅里叶分析是一种理想化的模型，其具有三个基本假设:线性、高斯性及平稳性，所以，其不适合用于非平稳信号的时频局部性能分析。而在动态称重系统中影响系统计量精度的主要因素是汽车行驶过程中产生的动态荷载对称重系统的干扰。车辆动态荷载的振动频率在3 ～20Hz 的低频范围，振幅变化可达静载的10%［7］，同时，由于轴载激励的动态称重系统承载部分的几何尺寸受到车辆双联轴轴间距和轮胎与地面接触长度的限制［8］，所以，采取常规的滤除周期性抖动信号的处理方法效果不佳。积分法需要较长的数据才能保证其精度，而且，当车辆通过过快时则不能得到预期测量精度。参数估计法可以解决车速的问题，而且通常一个周期就可以得出满意的结果，但是其前期对于动态称重系统的称台建模必须十分精确，这也是十分困难的。利用神经网络技术可以避开复杂的物理建模，但是仅根据系统的输入输出数据进行黑箱建模，这种方法需要各种运动状态下的汽车称重信号作为输入样本，于是，本文提供一个综合来看更好的解决算法——HHT。

2 HHT

1998 年，美国华裔科学家Huang 提出了一种新型的非线性非稳态信号的处理方法:HHT。HHT 方法从信号自身特征出发，用经验模态分解(EMD)方法把信号分解成一系列的本征模态函数(intrinsic mode function，IMF)，然后对这些IMF 分量进行Hilbert 变换，从而得到时频平面上能量分布的Hilbert 谱图，可以准确地表达信号在时频平面上的各类信息。

HHT 技术包含EMD 和Hilbert 变换两个部分。首先，将获得的信号所有局部极大值点采取三次样条插值函数法取得上包络，用信号的所有局部极小值点取得下包络，经过多次分解去除叠加波后使得波形更加的对称，以确定其瞬时平衡位置，这使得获得的IMF 分量经Hilbert 变换后得到的瞬时频率(instantaneous frequency，IF)更加有意义［10］。这样原始信号经过EMD 后就可以表示为

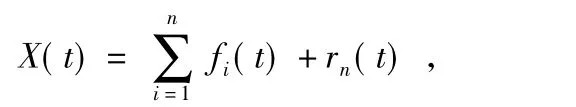
式中 X(t)为原始信号，fi(t)为经过EMD 后得到的各个IMF 分量，rn(t)为残余分量。

经过Hilbert 变换后可以得到

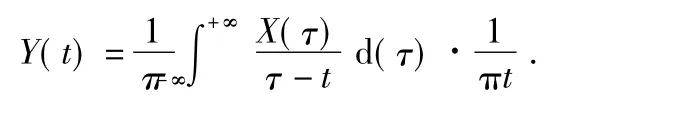
通过这个定义，X(t)和Y(t)行成了一个共轭复数对，于是可以得到一个解析信号Z(t)如下

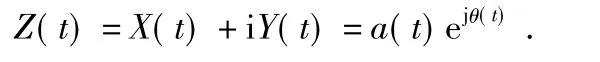
其中

从理论上讲，虚部的定义方法有很多种。但是Hilbert变换为其提供了一个唯一的虚部值，这就使得其结果成为一个解析函数。得到了相位，就可以得到瞬时频率，因为瞬时频率就是相位导数

其中，ω 为时间t 的单值函数，任何时间只有一个值，只能描述一个分量。

进行Hilbert 谱分析时，忽略了剩余分量rn(t)，因为其为一个单值函数或者是常数。每个IMF 分量的幅值和频率都是时间t 的函数，幅值的变化和瞬时频率的变化提高了信号分解的效率，而且使得这种分解更适用于分析非平稳信号。随着IMF 分解的进行，时间、幅值和频率被分成三个不同的信号，这样一个信号就形成了这三者的三维信号图，其中，幅值用时频平面中的等高线表示，这种幅值的时频分布，便称为Hilbert 谱。

3 HHT 动态称重传感器非线性信号的处理

本文选用某公司小货车(2 轴)为实验对象，车重2 500 kgf，负载3 000 kg 砝码，通过秤台的平均速度为10.188 km/h，由称重传感器采集数据，采样频率512 Hz，未采用HHT 信号处理前的原始数据波形如图3 显示。

图3 原始数据Fig 3 Initial datas

取其中一段进行EMD，结果如图4 所示。其中，图4(a)的为原始信号，图4(b) ～(f)依次为各阶IMF 分量，最下面的为剩余分量，它的均值即为真实轴重。

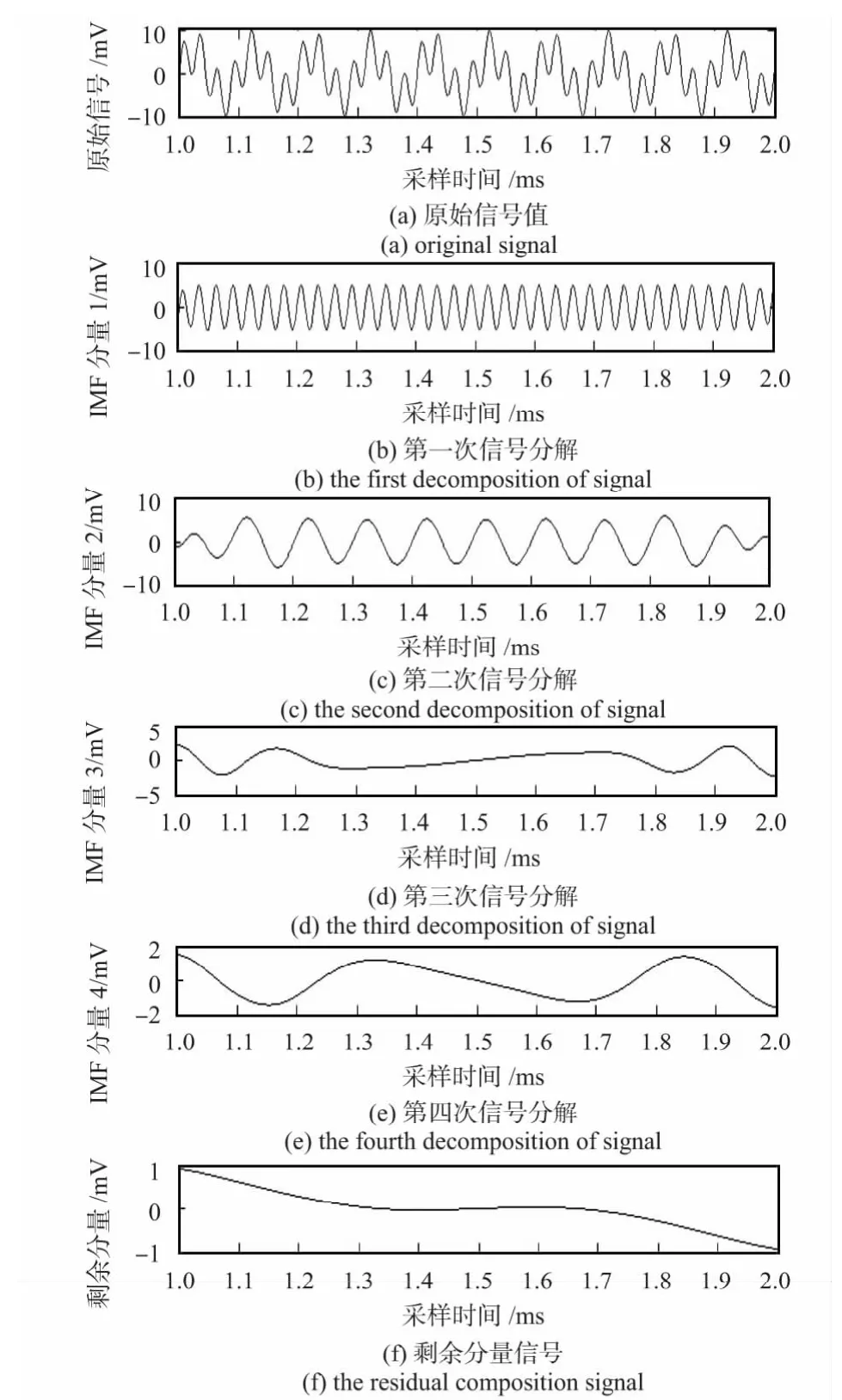
图4 EMD 图Fig 4 Drawing of EMD

经过HHT 后的数据和原始数据的对比图如图5 所示。由图5 可以看出:经过HHT 后信号曲线平滑，有效去除了各种低频干扰。

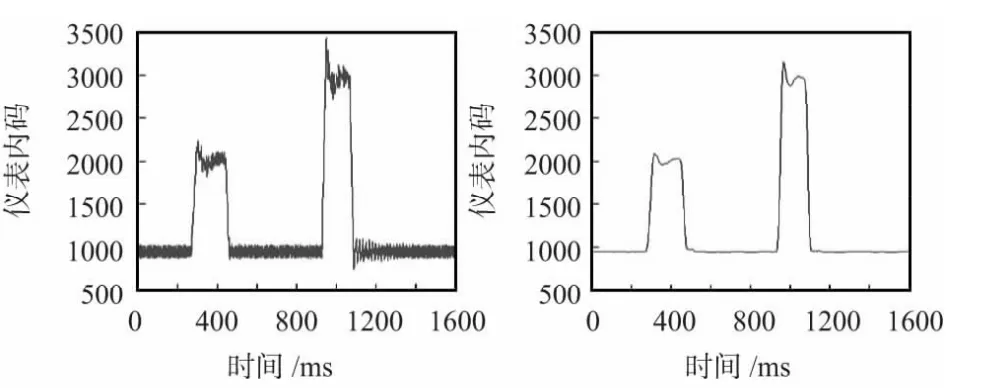
图5 信号处理前后效果对比图Fig 5 Contrast diagram of effect before and after signal processing

4 结 论

实验结果表明:经过HHT 后的信号，具有更高的分辨率与准确性，数据曲线更加平滑，对汽车动态轴重信号作EMD，去除各阶动态分量，用剩余分量的平均值代替真实轴重，这种方法可以有效地控制信号噪声干扰，得到更加准确的数据。

［1］ 许 嘉，蔡 萍，周志峰，等.二分梯形法在汽车动态称重中的应用［J］.微计算机信息，2005，21(4):22－23.

［2］ 吴 杰，费玉华，于劲松，等.汽车动态称重中的一种信号处理方法［J］.北京航空航天大学学报，2007，33(9):1041－1045.

［3］ 凌 杰，龙水根.优化算法在汽车动态称重系统中的应用［J］.西安公路交通大学学报，2001，21(3):77－79.

［4］ 张 雨，贺曙新，文绍波.汽车动态称重信号的两个处理方法［J］.南京工程学院学报:自然科学版，2004(4):105－108.

［5］ 袁明新，张 勇，张 雨.基于RBF 网络的动态称重系统设计［J］.交通与计算机，2003(2):60－63.

［6］ 章步云，周书民.非平稳信号的快速傅里叶变换与小波分析的比较［J］.通信技术，2002(7):1－2.

［7］ 王孝林.动态汽车衡及其检测［J］.衡器，1998(5):9－18.

［8］ 代 伟.高速公路动态称重系统关键问题的研究［D］.西安:长安大学，2008.

［9］ Bhatnagar G，Raman B.Robust watermarking using distributed MR-DCT and SVD［C］∥Advances in Pattern Recognition，2009:21－24.

［10］钟佑明，金 涛，秦树人.希尔伯特—黄变换中的一种新包络线算法［J］.数据采集处理，2005，20(1):13－17.