旋转式FBG 粘度计设计与有限元分析*

周延辉，谢 涛，张长胜，李英娜，赵振刚，李 川

(昆明理工大学 信息工程与自动化学院，云南 昆明650500)

0 引 言

粘性是液体的一个重要特征，衡量粘性大小的量被称为粘度，它是在液体受到外力作用移动时，分子间产生内摩擦的一个量度，而用于量化粘度的技术就称为液体粘度测量技术［1］。常用于测量粘度的应变式传感器是通过测量各类弹性元件的转矩或应变来间接测量液体粘度。目前，旋转法是粘度测量中最普遍的方法［2，3］，各类旋转式粘度计经常采用筒状的弹性元件作为敏感元件。

本文在传统旋转式圆筒粘度计结构的基础上，与光纤Bragg 光栅(FBG)［4，5］传感技术相结合设计了一种旋转式FBG 粘度计。首先对转旋式FBG 粘度计的结构特性和理论基础进行介绍，运用ANSYS 软件建立传感器的主体结构的仿真模型。然后，依据实际工作环境进行边界条件的处理并求解，得出粘度传感器的传感特性。根据有限元分析结果，得出粘度传感器的相关传感特性，由此可以确定FBG的最佳粘贴位置，并为传感器的设计和改进提供了可靠依据。

1 旋转式FBG 粘度计的结构与原理

传统的各类旋转式粘度计的测量原理基本相同，测量依据多是牛顿粘性定律。仪器由同步电机提供一个稳定的旋转速度，连接带刻度的圆盘，通过游丝和转轴带动转子旋转，如果转子未受到液体的粘性阻力，那么，指针会指向0刻度;反之，当转子受到液体的粘滞阻力，会使游丝产生相应的扭矩［6］，此时指针会有一个相对的读数，将读数乘以特定的系数就可得到液体的粘度值。

在传统的旋转式粘度计的基础上，使用FBG 技术，设计出了旋转式FBG 粘度计。其测量原理略有不同，采用弹性空心圆柱体作为弹性元件，下面连接有定子。此定子与转子类似都是接触元件，与被测液体相接触，不同的是定子固定不动，同步电机带动被测液体旋转。FBG粘贴于弹性空心圆柱体内壁，当液体对定子产生的扭矩传递到弹性空心圆柱体上，就会引起FBG 中心波长的移位，再通过特定的系数将波长位移量换算成液体的粘度值。图1 为旋转式FBG 粘度计测试平台。旋转式FBG 粘度计主体传感结构为弹性空心圆柱体与定子相连，如图2 所示。

图1 旋转式FBG 粘度计测试平台Fig 1 Test platform of rotary FBG viscometer

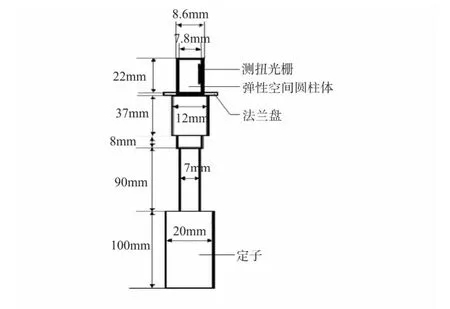
图2 传感结构Fig 2 Sensing structure

在图2 中，旋转式FBG 粘度计的传感结构［7］主要由以下3 个部分组成:

1)FBG:传感元件，通过Bragg 波长移位反映出粘度值。

2)弹性空心柱体:换能结构，采用硬铝合金材料，把定子受到的扭矩转换成FBG 的波长移位，测扭光栅粘接于弹性空心柱体的内壁上。弹性空心圆柱体的上端将与矩形支架相连，起固定作用。

3)定子:接触部分，它的上端通过法兰盘与弹性空心柱体相连。

弹性空心圆柱体的扭矩M 与FBG 波长位移量呈线性关系

其中，K1为常系数，ΔλB为波长位移量。

而液体的动力粘度又与扭矩M 呈一定的比例关系

式中 μ 为液体的动力粘度，K2为常系数。

由此可知，被测液体的动力粘度与FBG 的波长位移量ΔλB呈线性关系

式中 K 为粘度系数，它是由粘度传感器的结构和弹性空心圆柱体的材料所决定的。

在实际测量中，粘度计需要保持水平状态，使得外筒内的液体与定子均匀接触。同时，为了方便比较不同液体的粘度值，需要给液体一个相同的旋转速度。

不同液体在相同转速下与传感结构发生相对转动，由于牛顿流体的粘性或非牛顿流体的流变性对定子产生扭矩，定子将扭矩传递给弹性空心柱体，从而引起测扭光栅的不同程度的拉压变化，即产生相对应的FBG 波长移位。由此，经过计算可以间接地测出液体的粘度。

2 有限元分析

2.1 形变与受力分析

由上述理论分析可知，FBG 旋转式粘度仪的传感器主体结构由定子与弹性空心圆柱体相连接组成。固液接触是FBG 旋转式粘度仪测量液体粘度的一个重要特点，对其进行仿真研究属于耦合场分析。为了更好地观察和分析，本次仿真使用3D 建模。首先，依据传感器的结构，选择合适的材料，按照传感器的尺寸建立物理模型，分别对固体和液体划分网格，如图3(a)。然后，依据实际测量环境设置边界条件，即在弹性空心圆柱体上端施加一个位移约束;给液体施加一个44 r/min 的转速，如图3(b)。

图3 网格划分与施加约束效果图Fig 3 Meshing and impose restriction effect diagram

相关参数设置完毕后，进行求解，得出传感器的形变和应力强度云图，如图4 所示。

如图4 所示，定子受到旋转液体的粘性阻力作用，产生一个扭矩，定子将这个扭矩传到弹性空心圆柱体，从而引起弹性元件产生扭转形变。应力强度图很好地验证了旋转式FBG 粘度仪的这一特点，特别是弹性空心圆柱体部分变化明显，与预期相符，因此，FBG 贴于弹性空心圆柱体内壁最为适宜。现场试验也得出相同的结论:相比于弹性空心圆柱体顶部和外侧，将FBG 粘贴在弹性空心圆柱体内壁中心波长变化最明显，灵敏度最高。

图4 形变与应力云图Fig 4 Deformation and stress nephogram

2.2 路径分析

为了更好地验证仿真与理论的一致性，路径分析可以通过具体的数据，更准确地反映出空心圆柱体因液体粘度值改变而引起的不同的扭应变状况。在弹性空心圆柱体上，由上而下选取沿Y 轴方向的两点，分别显示出这两点间路径上的形变量变化曲线图(图5)与位移变化云图(图6)，改变流体材料的粘度值后，上述两种图形都会产生变化。

在弹性空心圆柱体轴向上选取固定的两个点进行路径分析。结果显示:设置粘度参数分别为0.5，0.75，1.5 Pa·s，得出路径上的最大微应变分别为2.578×10－6，3.836×10－6，7.502×10－6，扭转角度分别为1.32°，2.04°，3.83°。

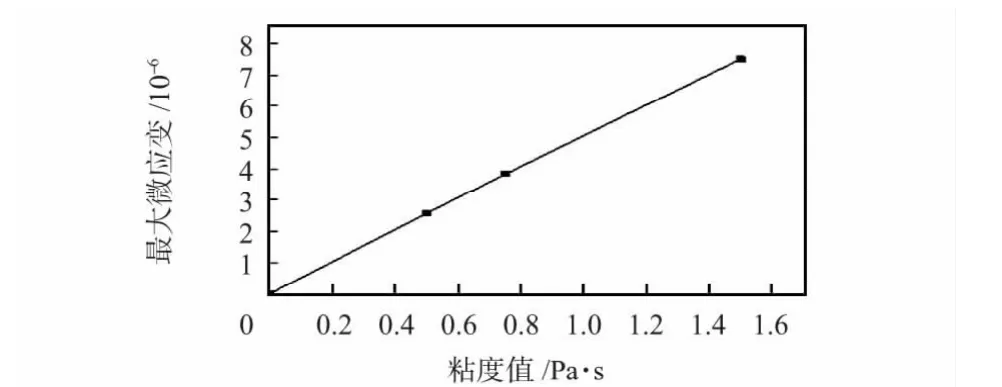
图5 最大微应变与粘度值关系图Fig 5 Relationship between the maximum micro-strain and viscosity values

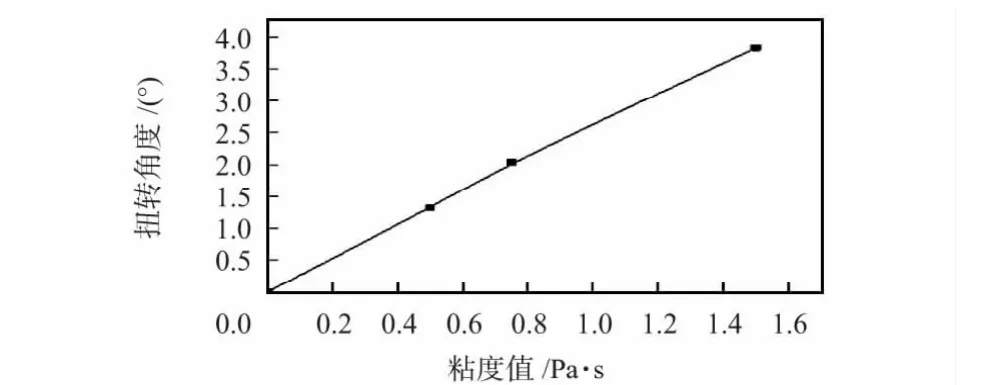
图6 扭转角度与粘度值关系图Fig 6 Relationship between twist angle and viscosity values

图5 和图6 表明:在液体旋转速度相同的条件下，液体粘度值的变化会引起弹性空心圆柱体最大微应变和扭转角度的变化，且几乎都呈一定的线性关系。这说明弹性元件的扭应变量随液体粘度值呈线性变化，符合理论的预期。由此可知，传感器结构设计合理，符合粘度测量的要求。

3 结 论

本文提出了一种基于FBG 传感技术的旋转式粘度计的传感结构。通过有限元分析对粘度传感器的结构和尺寸进行改进，并得出了粘度传感器的传感特性。定子将扭转阻力传递到弹性空心圆柱体，使之产生扭转形变，路径分析可以提供更为具体的形变数值，仿真结果直观地反映了弹性元件的形变情况和受力分布，确定了FBG 的粘贴位置。有限元分析表明:改变液体的粘度值能够对测扭传感器扭转形变产生影响，最大形变量、扭转角度均与施加液体的粘度值呈一定的线性关系，验证了旋转式FBG 粘度计设计的合理性。

［1］ 陈惠钊.粘度测量［M］.修订版.北京:中国计量出版社，2003.

［2］ 祁海洋.高压旋转粘度计的研制及合成油压粘特性研究［D］.哈尔滨:哈尔滨工业大学，2011.

［3］ 吕仲兰.旋转粘度计检定中的不确定度来源及影响因素控制［J］.化学分析计量，2004，13(5):48－49.

［4］ 李 川，李英娜，万 舟，等.光纤传感器技术［M］.北京:科学技术出版社，2012.

［5］ 孙圣和，王延云.光纤测量传感技术［M］.哈尔滨:哈尔滨工业大学出版社，2000.

［6］ 张伟刚，赵启大，开桂云，等.新型光纤光栅扭转传感器研究［J］.光子学报，2001，30(10):1237－1239.

［7］ 肖军民，陈国香.一种新型旋转式数字粘度仪的研究和开发［J］.计量与测试技术，2003，30(5):287－289.