液晶缺陷对对称结构光子晶体透射特性的调制作用

蒙成举，戚朝伟，杨德贵

(河池学院 物理与机电工程学院，广西 宜州 546300)

0 引言

自光子晶体概念［1］提出以来，有关光子晶体理论和应用一直受到人们广泛关注，目前已涉及到光子晶体滤波器、光子晶体开关和光集成放大器等应用方面的研究［2－5］。光子晶体滤波器是重要的光无源器件之一。它在光通信、光学测量、光谱分析和光传感等应用领域中，要求光滤波器件具有窄带和可调谐特性，目前很多光子晶体的研究报道中几乎所有的光子晶体器件都是不可调谐的，这极大的限制了光子晶体在这些应用领域中的发展。所幸的是1999年Kurt Bush等首次将向列相液晶作为缺陷引入反蛋白石结构三维光子晶体中，同年K.Yoshino又报道了填充液晶的合成欧泊型和反欧泊型可调光子晶体波导，开创了液晶在光子晶体中应用的先河［6］，因向列相液晶材料是有序性的流体以及它在外场作用下，能产生热光、电光或磁光效应［7］，当液晶温度变化时，向列相液晶的双折射将发生变化，而引起光子晶体透射谱发生移动，从而达到调制的目的。而一维光子晶体具有引入缺陷工艺简单、易集成、成本低、易多元化和良好的调制性能，将在未来以光子为载体的全光网络中发挥重要作用，因此利用向列相液晶的这种物理特性，可实现光子晶体缺陷模的调制作用，既能避免重复制备光子晶体的工序，还能大大的节省原材料成本，液晶无疑是一维光子晶体滤波器很好的调制材料。

基于此，本文首先分析液晶材料热光效应的温度特性及其在对称结构光子晶体中的缺陷特征，然后分析液晶温度以及它的厚度对该光子晶体缺陷模的调制规律，从而为可调谐光子晶体滤波器的设计提供理论参考。

1 研究模型及理论方法

1.1 液晶缺陷光子晶体模型

引入向列相液晶缺陷的一维对称光子晶体结构模型如图1所示。在两块平板玻璃H上镀有高低折射率交替排列的介质A、B，组成了对称结构光子晶体，在对称结构光子晶体中间灌入液晶形成的液晶盒作为光子晶体的缺陷层，在液晶层两侧的光子晶体中各介质的折射率分别为na=1.38，nb=2.35，相应各介质的厚度分别为da=db=λ0/4，中心波长 λ0=1.55 μm。

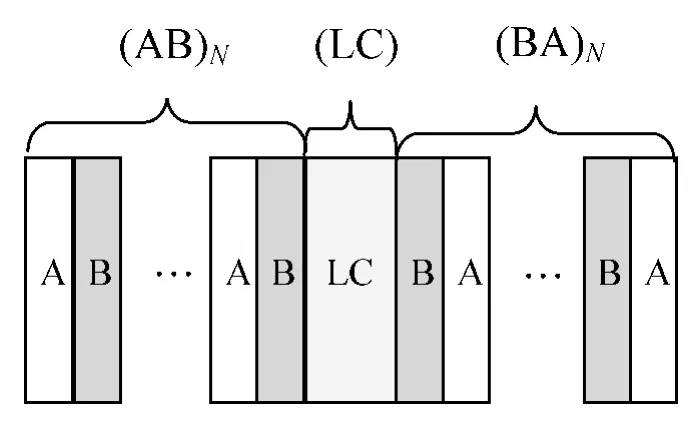
图1 液晶缺陷光子晶体模型

不考虑其它因素的影响，向列相液晶可看成是一种单光轴材料，具有两种折射率，通常称之为双折射，这种液晶材料具有很好的热光效应。当温度处在维持液晶相的范围内时，其值的变化都会使液晶的光学性质发生相应的变化，这些光学性质其中就包括了液晶的双折射。根据钱德拉塞卡尔(S.Chandrasekhar)的研究［8］，液晶双折射率与温度的变化关系可以用下式表示:

式中，no、ne分别是寻常光(Ordinary ray)折射率和非寻常光(Extraordinary ray)折射率，则定义的双折射率为Δn=ne－no，ρ0和ρ为液晶在向列相—各向同性液相相变点及温度T时的密度，由于温度变化对密度的影响很小，因此ρ/ρ0可以近似为常数。

后来Vuks在上式的基础上，考虑液晶分子的微观参数后对双折射率与温度的关系做了修正，经过大量的实验研究后，最终得出液晶双折射率的实验公式［9］:

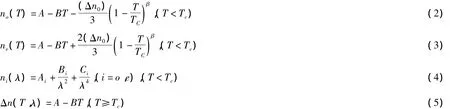
其中，Δn0表示温度T=0时液晶的双折射，Tc是液晶在向列相—各向同性液相的相变点时的温度，A，B可以近似为常量，β和柯西系数Ai，Bi，Ci都是关于温度的函数，这些参量都是由液晶材料决定，这里均采用UCF－35文献［10］的参数。

1.2 研究理论方法

在液晶层两侧的N个周期叠堆而成的薄膜常采用传输矩阵法理论［11］。因此，两侧介质A和B组成的基本周期单元的传输矩阵为:

而对于液晶层，当入射光沿向列相液晶的光轴方向入射时，则有两个主方向，分别为μ、ν，设μ为快轴方向，若入射光与出射光的关系满足［12］

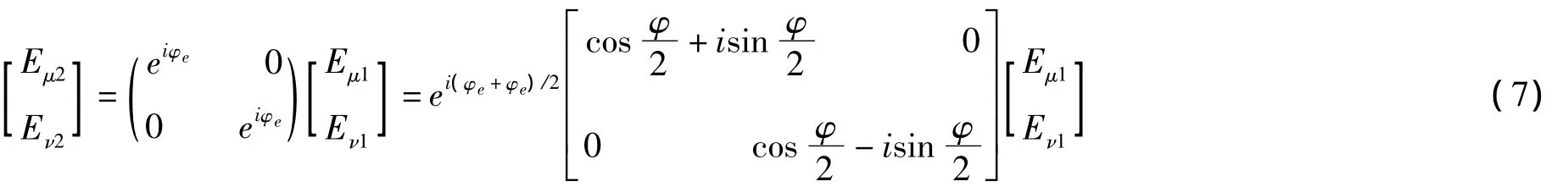
在填充液晶材料时设计的液晶盒作为偏光器件，此时可以将其视为一个相位延迟片，光学中关于偏振光传播的问题一般通过琼斯矩阵来解决，所以对于整个液晶盒的琼斯矩阵，可写为［12］:

偏光器件必须满足(9)式的两个条件才能发生谐振，即光子晶体中才会出现液晶缺陷模。式中λ是入射光波的波长，d为液晶层的厚度，根据传输矩阵理论，可以得到光在光子晶体中传播时的总传输矩阵为:

若光子晶体置于空气中，且光垂直入射到光子晶体时，根据传输矩阵理论，可算出光子晶体的透射系数为:t=2/(M11+M12+M21+M22)，透射率为:T=t·t*.

2 数值计算结果与分析

2.1 加入液晶缺陷前后的光子晶体透射谱

保持其他参数不变，光子晶体重复周期数N=8，液晶温度T=280 K，厚度d=0.2 μm时，分别计算模拟光子晶体(AB)8(BA)8和(AB)8(LC)(BA)8的透射谱，结果如图2所示。

从图2(a)我们知道，对称结构光子晶体(AB)8(BA)8，约在1.75 μm ～2.55 μm的波长范围内出现较宽的光子禁带，且在禁带中位于2.067 μm位置处出现一条缺陷模，从介质的排列规律来看，AB…AB和BA…BA中间缺一个A，形成了空位缺陷，因此禁带中会出现一条缺陷模，这里称之为空位缺陷模。这也是对称结构光子晶体透射谱的特征之一［13］。当在光子晶体膜层的中间位置插入液晶盒(灌入向列相液晶材料)后，光子禁带边缘的通带透射率由99.5%迅速衰减到10%左右，同时禁带中出现高透射率的双缺陷模，如图2(b)所示。这是因为插入液晶后液晶与两边B介质形成了两个边界，由于光进入液晶后产生了相位延迟效应，使得前行波和反向波相遇而发生共振隧穿效应，导致了液晶缺陷模的出现，从而形成了双缺陷模透射谱特征。进一步研究发现，液晶缺陷模的位置强烈依赖于液晶层的厚度d及其温度T，为了寻找液晶对透射谱的调制规律，下面将分析并讨论液晶层的厚度以及环境温度对光子晶体透射谱的具体影响规律。

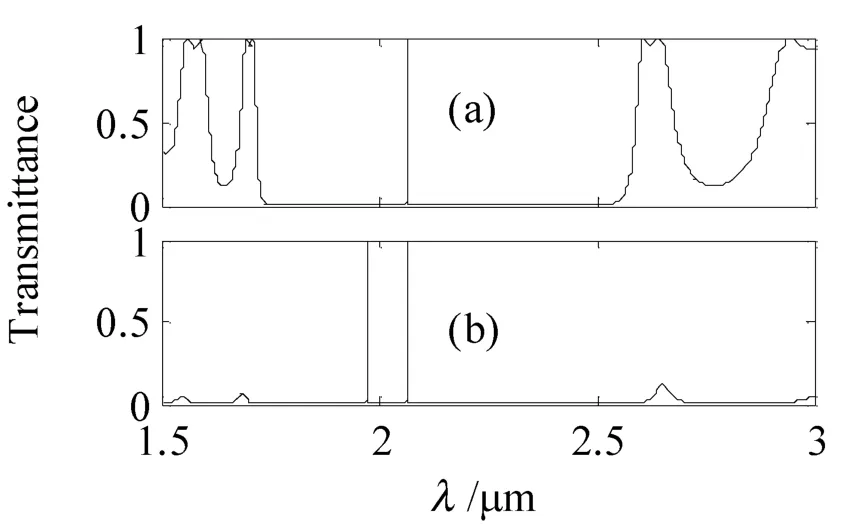
图2 光子晶体透射谱(a)(AB)8(BA)8(b)(AB)8(LC)(BA)8

2.2 液晶层厚度对透射谱的影响

在T=280 K温度条件下，固定其他参数不变，使液晶层的厚度d=0.25，0.5，1.0 μm时，计算模拟出液晶缺陷光子晶体透射谱如图3所示。

从图3我们可以观察到，随着液晶厚度的增大，液晶缺陷模有向空位缺陷模靠拢的趋势，同时禁带边缘透射率迅速下降。当d=0.25 μm时，两条缺陷模的位置，分别位于1.991 μm、2.067 μm处，且禁带边缘的透射率约为9.5%，如图3(a)所示;当厚度增加到d=0.5 μm时，液晶缺陷模的位置向长波方向移动到2.027 μm处，而空位缺陷模保持原来的位置不动，禁带边缘的透射率降到0.5%左右，如图3(b)所示;当厚度增到d=1.0 μm时，液晶缺陷模几乎与空位缺陷重合，但是空位缺陷模的位置依然未变，且禁带边缘透射率几乎为0，如图3(c)所示。

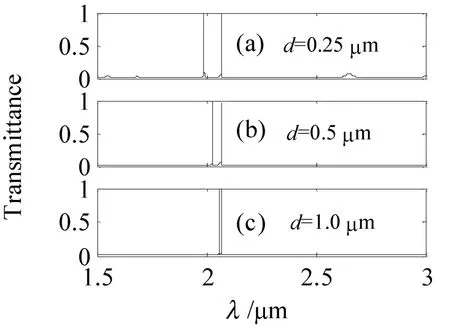
图3 液晶层厚度对透射谱的影响

2.3 温度对光子晶体的透射谱的影响

同理其它参数不变，取温度T=280、290、300 K时，分别计算光子晶体(AB)8(LC)(BA)8的透射谱，如图4所示。

从图4可以看到，随着液晶温度的升高，液晶缺陷模的位置向短波方向移动，但其透射率没变，而空位缺陷模不受液晶温度的影响。当T=280 K时，液晶缺陷模位于1.974 μm处，空位缺陷模位于2.067 μm处，且透射率均为100%，如图4(a)所示;当温度升到T=290 K时，液晶缺陷模的位置向短波方向移动到1.97 μm处，而空位缺陷模没有发生移动，如图4(b)所示;当温度升到T=300 K时，液晶缺陷模移动到1.963 μm处，而空位缺陷模仍然位于2.067 μm处，如图4(c)所示。

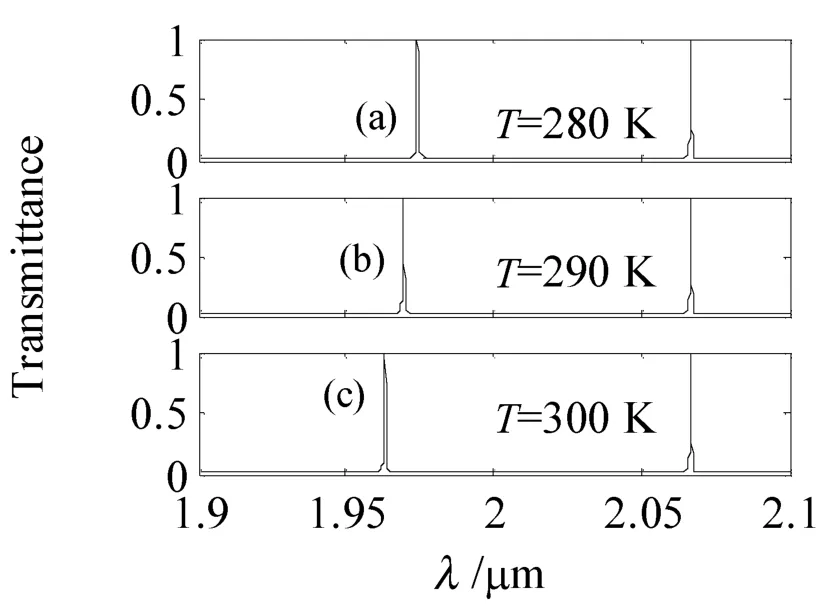
图4 温度对缺陷模的影响

3 结论

利用液晶热光效应的温度特性，并通过传输矩阵法理论研究对称结构液晶缺陷一维光子晶体的光传输特性，得出如下结论:

(1)当无液晶缺陷时，在较宽的禁带范围出现一条缺陷模，这个缺陷模出现是因介质排列的缺省而形成的空位缺陷所引起的。

(2)当在光子晶体引入液晶缺陷时，禁带边缘通带的透射率大幅下降，同时禁带中出现高透射率的液晶缺陷模和空位缺陷模，构成了双模特征，可设计双通道光子晶体滤波器件。

(3)随着液晶温度的升高液晶缺陷模的位置出现蓝移，随着液晶层厚度的增大其缺陷模出现红移，且缺陷模的透射率均保持在100%不变，可利用液晶具有独特的物理特性来调制所设计的光子晶体器件。

因此，液晶缺陷对对称结构光子晶体呈现的这些调制规律，对设计光子晶体宽频段全反射镜和可调谐光子晶体滤波器具有理论指导意义。

［1］S John.Strong localization of photons in certain disordered dielectric superlattices［J］.Phys Rev－ Lett，1987，58(23):2 486 －2 489.

［2］宋俊峰，常玉春，王海嵩，等.光晶体光波导传输特性研究［J］.中国激光，2002，23(10):1 237 －1 240.

［3］苏安，蒙成举，高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制［J］.中国激光，2014，41(3):0306001.

［4］蒙成举，杨德贵，戚朝伟.实现多系双通道滤波功能的异质结构光子晶体［J］.河池学院学报，2014，34(5):87－91.

［5］蒙成举，韦吉爵，韦兰香.实现双系多通道光滤波功能的双周期光子晶体［J］.河池学院学报，2013，33(5):29－32.

［6］Yoshino K，Shimoda Y，Kawagishi Y，et al.Temperature tuning of the stop band in transmission spectra of liquid－ crystal infiltrated synthetic opal as tunable photonic crystal［J］.Appl.Phys.Lett.，1999，75(7):932 －934.

［7］王新久.液晶光学和液晶显示［M］.北京:科学出版社，2006.

［8］S Chandrasekhar.Liquid crystal(2rd ed.)［M］.Cambridge:Cambridge University Press，1992.

［9］陈兵，徐寿颐.大的双折射色散液晶材料［J］.化工新型材料，2001，29(6):13－17.

［10］Jun Li，Shin－ Tson Wu.Self－ consistency of Vuks equations for liquid－ crystal refractive indices［J］.J.Appl.Phys.，2004，96(11):6 253 －6 258.

［11］王辉，李永平.用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50(11):2 172－2 178.

［12］阎吉祥，魏光辉.矩阵光学［M］.北京:兵器工业出版社，1995:188 －197.

［13］蒙成举，苏安.吸收对镜像对称一维光子晶体透射谱的影响［J］.激光与红外，2011，40(11):1 248－1 252.