三种重力加速度实验测定方法的比较研究

梁玉娟，钟友坤，韦兰香，许敏明，邓卫娟

(河池学院 物理与机电工程学院，广西 宜州 546300)

重力加速度是一个重要的地球物理常数，其大小一般由物体所在地区的纬度和海拔高度以及矿藏分布等因素决定，准确测定它的量值，无论在理论上，还是在科研和工程技术等方面都有极其重要的意义，在大学基础物理中，测定重力加速度是一个重要的必做实验。2011年，我校新采购了一批实验设备，测定重力加速度的实验设备也得到了全面更新，FB327型单摆实验仪、FB210C型复摆实验仪、FB210E型自由落体实验仪分别代替了原有的实验设备:单摆、钢板复摆、ZL－A自由落体仪。以下将对这三种新设备测定重力加速度的实验方法及结果进行比较分析，探讨三种测定方法中误差产生的原理以及如何消除或减小误差产生的方法，新设备比旧设备有哪些优势，为实验操作者对比和选择测定方法提供依据，为实验教学者提供教学参考。

1 单摆法原理及测量结果

1.1 实验原理

把一个金属小球挂在一根细长的线上，如图1所示，如果细线的质量比小球的质量小得多，而小球的直径又比细线的长度小得多，那么，这个装置可以看作无质量的细长线系住一个质点，这样的装置就是单摆。在忽略空气阻力、浮力、细线的质量及伸长等因数，同时在摆角很小的情况下，单摆的振动可看作简谐振动，它的振动周期T为［1－3］:

式中L是单摆的摆长，其长度为悬挂点O到小球球心的距离，g是重力加速度，因此，只要测量出摆长L和振动周期T值，就可以计算出重力加速度g。在实验中测量连续摆动n个周期的时间t，T=t/n，代入(1)式得重力加速度的计算公式［2］

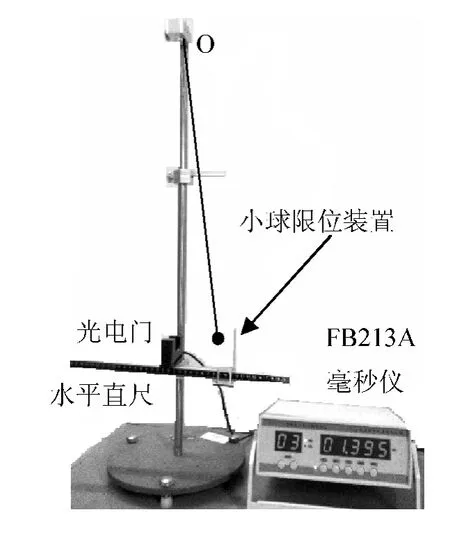
图1 FB327型单摆实验仪

1.2 实验方法及结果

本实验采用FB327型单摆实验仪，如图1所示［3］，调节摆线长度，并根据摆球位置将光电门固定在下方适当位置，使小球正好能启动光电门。采用FB213A光电计时计数毫秒仪自动计时，调节计时器，预置计时周期次数为15个周期。调节好小球限位装置，使摆角θ≤15°。由于小球放手时的不一致性，因此在同一摆角处多次测量取平均值。实验中固定摆长，取L=58.6 cm(摆线+球半径)，用FB213A光电计时计数毫秒仪测量连续摆动15个周期的时间t，见表1。

表1 单摆连续摆动15个周期的时间

将L=58.6 cm、n=15、t=22.936 6 s代入(2)式得g=989.42 cm/s2。

以往单摆实验都限于小角度(θ＜5°)内做近似等周期摆动，用秒表测量小球振动周期［2］。本实验摆角可取θ≤15°的范围，而且有水平直尺及小球限位装置，能保证每次实验小球在铅垂面内摆动且摆角相同，而使用旧设备不能达到这一点;计时器精度为0.001 s，每次测量不确定度小于0.001 s，精确度比以往用秒表测时间精确得多;又由于空气阻尼的存在，摆角随时间的延长而衰减，以往单摆实验法无法精确测得大角下摆动周期的准确值，现采用光电传感器和电子计时器实现自动计时之后，能够在很短几个振动周期内准确测得单摆在大角下的周期，这样可以忽略空气阻尼对摆角的影响。

2 复摆法原理及测量结果

2.1 实验原理

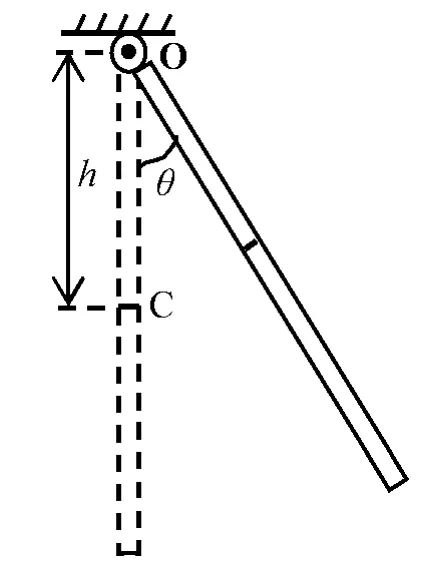
图2 复摆示意图

复摆是一个刚体绕固定的水平轴在重力作用下作微小摆动的动力运动体系。如图2所示，质量为m的刚体绕固定轴O在竖直平面内做左右摆动，刚体的质心C与轴O的距离为h，摆动角度为θ(θ＜10°)。若规定右转角为正，则刚体所受重力矩M与角位移 θ方向相反，即有［1，4－5］:

根据定轴转动定律，该复摆又有:

其中I为该刚体的转动惯量。由(3)式和(4)式可得:

此方程说明该复摆在小角度下作简谐振动，其周期为:

设IC为过质心C且与O轴平行的转轴的转动惯量，由平行轴定理可知:

将(7)式代入(6)式得:

根据(8)式，可以间接测量得当地重力加速度g。

对于固定刚体而言，过质心轴的转动惯量IC是固定的，因而实验时，只要改变质心到转轴的距离如h1、h2，则刚体摆动周期分别为:

为了使计算公式简化，取h2=2h1，合并(9)式和(10)式得［5］:

这样只要测出周期和高度就可以计算出当地的重力加速度了。

2.2 实验方法及结果

如图3所示，采用FB210C型复摆实验仪［5］，摆杆长60 cm，直径0.6 cm，质量0.132 kg，杆上有上、下二条标记刻线，h1=27.5 cm，h2=55 cm;两个质量相同的圆环形砝码块mA=mB=0.256 kg，外径4.4 cm，内孔径0.6 cm，高度2.2 cm，根据实验需要可以分别固定在杆上不同位置。计时器采用FB213B智能型数显计时计数微秒仪，精度为0.000 1 s。利用水平仪，调节复摆实验仪底座底脚螺钉使仪器底座处于水平状态;根据摆杆位置将光电门固定在下方适当位置，使摆杆能启动光电门;调节计时器并预置计时周期次数为10。按图3(a)、(b)所示安装好砝码，然后把复摆沿水平方向拉开一个角度θ＜10°，使摆杆的下端偏离平衡位置约5 cm，待复摆左右摆动平稳后，启动计时器测量复摆连续摆动10个周期的时间t10，并获得相应的周期T1、T2，见表2。

图3 FB210C型复摆实验仪

表2 复摆的振动周期

将h1以及周期T1、T2的平均值代入(11)式得g=1 040.03 cm/s2。

以往实验所用复摆是一均匀钢板，它上面从中心向两端对称地开一些小孔，测量时分别将复摆通过小圆孔悬挂在刀刃上，便可用秒表、直尺测出复摆绕不同回转轴摆动的周期和回转轴到重心的距离，然后通过作图法或最小二乘法求得重力加速度［4］。而使用新设备，距离不用测量，计时器精度又很高，显然测得结果精度更高，而且操作简单。

3 自由落体法原理及测量结果

3.1 实验原理

自由落体运动是初速度为零的匀变速直线运动，其运动方程为［1－2，6］:

其中h表示t时间内物体下落的高度，因此，只要测出h和t，就可求出重力加速度g。

3.2 实验方法及结果

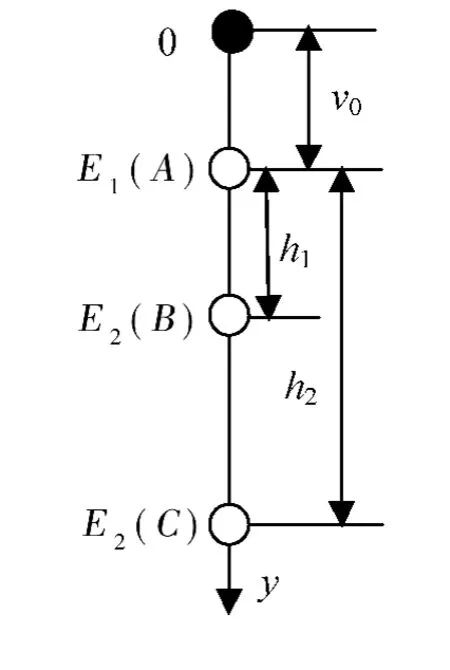
图4 自由落体法示意图

当不考虑空气阻力和小钢球直径影响时，重力加速度的测量误差主要来自初速度ν0、路程h及相应时间t的测量误差。在实验中h和t一般是容易准确测量的，但精确测量瞬时初速度ν0比较困难，要严格满足ν0=0也不容易做到，因此，要设法消除ν0对实验结果的影响，具体的测量方案如图4所示［2，6］。将光电门E1、E2固定在A、B位置处，两点之间的距离为h1。设小钢球沿竖直方向从“0”点开始自由下落，设它到达A点的速度为ν0，从A点起，经过时间t1后到达B点，有

若保持上述条件不变，A点光电门E1位置不变，将光电门E2下移至C处，经过时间t2后小钢球到达C点，令A、C两点之间的距离为h2，则有

由(13)、(14)两式可得:

因此，实验中只要测出h1、t1、h2、t2，就可以算出重力加速度。本实验采用FB210E型自由落体实验仪［6］，计时器采用FB213B型数显计时计数微秒仪，取h1=40 cm，h2=60 cm，测出对应时间t1和t2，如表3所示。

表3 小球经过不同位移的时间

将高度差h1、h2以及时间t1、t2的平均值代入(15)式得g=988.15 cm/s2。与ZL－A自由落体仪相比较，两者都是测量高度差，电脑计时，准确度都比较高，操作都比较简单，没有特别的优势。

4 三种方法测量结果对比与分析

地球表面重力加速度理论值可由下式计算得出［2］:

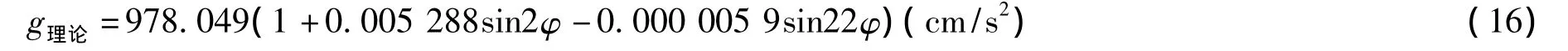
式中φ为纬度角，由经纬度GPS定位测量仪测得力学实验室位置海拔高度约150 m，经度108°39'24.0″，纬度24°30'3.6″。现不考虑地质状况及海拔高度的影响，仅考虑纬度的影响，将纬度角代入(16)式即得力学实验室所处位置重力加速度的理论值g理论=981.95 cm/s2。因此，三种测量方法所得结果的百分误差分别为:

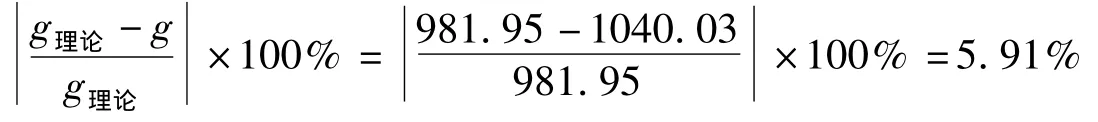
由上可知，三种新设备测得的结果误差都不大，单摆法、自由落体法测得的结果误差相对较小，而复摆法测得的结果误差相对较大，三种方法测得的重力加速度值与当地的重力加速度理论值还是很相近的。这三种方法都是采用光电传感器和计时计数毫秒仪测定时间，精度很高，不会像以前那样，用秒表测定时间，因个体差异而产生较大的误差，因此，时间测量误差可以排除。对FB327型单摆实验仪，公式(1)实际上是一个为简化实验操作以及数据处理的近似公式，实际实验时，空气浮力、空气阻力、悬线的质量、摆球的质量、摆角等因素都会给测量带来系统误差［7］;实验仪水平直尺上装有小球限位装置，可以减小摆角误差的影响，同时能保证小球在一个竖直平面内左右摆动，因此，测量误差主要来源于摆长的准确测定。对于FB210C型复摆实验仪，公式(3)也是一个近似公式，实际实验时，空气阻力、摆杆质量、砝码质量、刻度线位置等因素都会产生系统误差，但研究表明:当悬挂点到质心的距离较小且运动速度不大的情况下，复摆所受空气阻力可以忽略不计［8］;而当砝码在下刻度线时，悬挂点到质心的距离较大，摆动速度相应较大，此时空气阻力影响较大;本实验仪没有水平直尺，也没有摆杆限位装置，因此，不能保证每次实验时摆角一致，也不能保证摆杆在传感器所在铅垂面内摆动，摆角的不一致性以及摆杆发生一定的扭转摆动是误差的主要来源。对于FB210E型自由落体实验仪，小钢珠直径很小约7.8 mm，在有机玻璃管中自由落下，空气浮力和阻力对实验影响很小，在理论方法上排除了初速度ν0的影响，因此，测量误差主要来源于两光电门高度差的测定，文献［9］表明:实验时取较大的h2可以提高实验精度。复摆实验仪摆杆的质量及体积、砝码的质量及体积分别比单摆悬线和小钢球的大(小钢球直径约14 mm)，空气浮力和阻力影响相对较大，所以复摆法测量误差比单摆法的大;相对于摆长的测量，高度差更容易精确测定，因此，自由落体法测得的结果比单摆法测得的结果精度更高一些，是目前我校力学实验室重力加速度测量最简单、最佳方法。

5 结论

(1)三种测量重力加速度的新仪器，实验操作都比较简单，测得的结果都比较准确，在实验精度要求不太高的情况下，使用哪种方法均可以，但当实验精度要求较高时，最好是使用自由落体法测量。

(2)由上述对结果误差的分析可知，若这三种设备做如下一些小改进，将会进一步减小实验误差:对FB327型单摆实验仪、FB210E型自由落体实验仪，在竖直铁杆上附加一根竖直的刻度尺，可以减小测量摆长以及两光电门间距的误差;对于FB210C型复摆实验仪，像图1那样，增加一个水平直尺及摆杆的限位装置，可以减弱摆角误差以及防止摆杆发生扭转摆动。

(3)这三种设备都配备了光电传感器和高精度的计时计数毫秒仪，智能化程度高，掌握这两种新技术在自动测量和自动控制中的应用，有利于扩大学生视野，激发学生学习兴趣，提高教学效果。

［1］漆安慎，杜婵英.普通物理学教程·力学(第三版)［M］.北京:高等教育出版社，2012:225－226，288.

［2］覃以威.大学物理实验(Ⅰ)［M］.桂林:广西师范大学出版社，2010:28－31.

［3］杭州精科仪器有限公司.研究单摆的运动特性实验讲义［Z］.1－5.

［4］覃以威.大学物理实验(Ⅱ)［M］.桂林:广西师范大学出版社，2010:26－27.

［5］杭州精科仪器有限公司.复摆的特性研究实验讲义［Z］.1－3.

［6］杭州精科仪器有限公司.重力加速度的测定实验讲义［Z］.1－2.

［7］游艳琳，熊建文.单摆测重力加速度实验近似处理的误差分析［J］.物理通报，2013(5):92.

［8］张天洋，王艳辉，曲光伟，等.空气阻力对复摆振动周期的影响［J］.物理实验，2008，28(11):42－45.

［9］张兵，程洋，赵经博，等.用自由落体法测量重力加速度的实验误差分析［J］.物理与工程，2014(7):54－56.