Ti6Al4V合金的高温短时蠕变本构关系与应力松弛行为
2015-03-26杜舜尧陈明和谢兰生张成祥
杜舜尧,陈明和,谢兰生,张成祥
(南京航空航天大学 机电学院,南京 210016)
Ti6Al4V(即 TC4合金)属于 α+β型钛合金,具有密度小、比强度高、耐腐蚀性和耐热性好、热稳定性高等特点,因此广泛应用于航天、航空、化工、船舶和医疗等领域[1-4]。但是Ti6Al4V合金在冷成形工艺下的回弹量较大,零件的成形精度不高,因此,需要采用热成形并辅助热校形来解决这个问题,而应力松弛和蠕变行为则在热成形和热校形过程中起到了举足轻重的作用[5-7]。为此,国内外学者对Ti6Al4V合金的应力松弛和蠕变行为进行了大量的研究。HO等[8-9]将应力松弛、蠕变和时效理论相融合,建立了一种适用于铝合金材料的蠕变时效本构模型。陈缇萦等[10]研究了TC18钛合金的蠕变行为,分析了不同条件下TC18钛合金的蠕变激活能、蠕变机制以及蠕变温度与变形应力指数的关系。虽然当前国内外对Ti6Al4V合金的应力松弛和蠕变行为研究较多,但是实验的温度条件大多是在 700 ℃以下[11],对于 700 ℃以上高温条件下Ti6Al4V合金应力松弛行为的研究尚少。同时,大部分的研究是围绕长时间的蠕变行为分析,而对于短时蠕变行为的研究不多[12]。此外,SCHUH 等[13]大多是从能量、应力指数和显微组织等方面定性分析蠕变性能与机制,缺乏对应力松弛与蠕变之间定量关系表达式的研究。因此,研究Ti6Al4V合金高温短时蠕变本构关系与应力松弛行为可以为以后的工程应用提供指导性的依据。
本文作者对Ti6Al4V合金板材在不同的温度、初始应力和预应变条件下进行了多组应力松弛试验,基于试验数据,研究了高温下Ti6Al4V合金板材的应力松弛行为以及工艺因素对其的影响,并且构建了不同条件下的应力松弛方程和高温短时蠕变本构方程。最后,通过有限元分析验证了高温短时蠕变本构模型的可靠性。

表1 Ti6Al4V合金的化学成分Table 1 Chemical composition of Ti6Al4V alloy (mass fraction, %)
1 实验
本试验中所用的材料是退火态的Ti6Al4V合金板材,厚度为1.5 mm,具体化学成分见表1。试验仪器为RG2000-20型电子万能拉伸试验机和PID温控仪。应力松弛试验开始前,通电加热到预定温度后保温 5 min,之后开始加载,应力松弛时间设定为2400 s。试验所用试样的规格如图1所示。
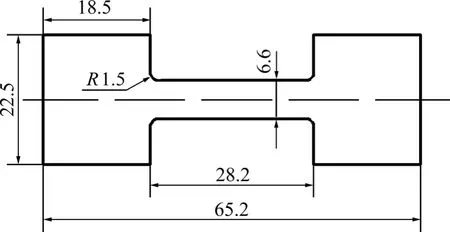
图1 试样尺寸(单位:mm)Fig. 1 Size of specimen (unit: mm)
2 结果与分析
2.1 应力松弛特征
图2所示为初始应力相同时Ti6Al4V合金板材不同温度下的真实应力松弛曲线。
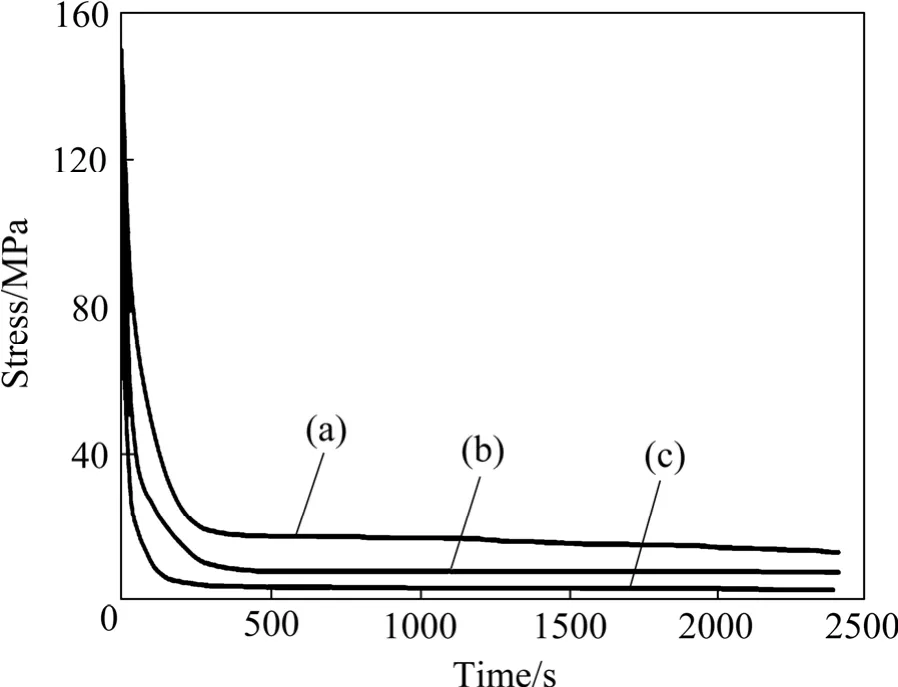
图2 不同温度下Ti6Al4V合金的真实应力松弛曲线Fig. 2 True stress relaxation curves of Ti6Al4V alloy at different temperatures: (a) 650 ℃; (b) 700 ℃; (c) 750 ℃
由图2可以看出,在650~750 ℃的温度范围内,Ti6Al4V合金板材的应力松弛可以分为两个阶段。第一个阶段应力松弛速率很快,剩余应力急剧降低,该过程为应力松弛的前250 s。第二个阶段应力松弛较为缓慢,经过2000 s后剩余应力趋向于应力松弛极限。采用式(1)对应力松弛行为进行描述[14]:式中:0ε为初始应变;eε为弹性应变;pε为塑性应变。其中0ε为一定值,eε和pε均为变化值。在应力松弛过程中,pε随着时间的增加而不断增大,eε则不断地减小,从而使得回弹应力随时间的增加而减小,这就是应力松弛现象。

2.2 工艺因素对Ti6Al4V合金板材应力松弛的影响
由图2可以发现,温度对应力松弛的影响十分显著。在第一个阶段,应力松弛速率随着温度的升高而增加,应力松弛极限随着温度的升高而减小。温度对应力松弛的影响可以用下式描述[15]:
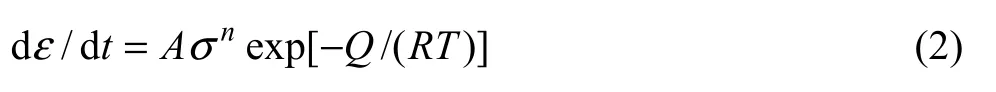
式中:ε为塑性应变;t为时间;A为常数;σ为应力;Q为热变形激活能;R为摩尔气体常数;T为热力学温度。在确定的变形机制下,Q是定值,此时,塑性应变速率随着温度的升高而增加。因此,单位时间内弹性形变转化为塑性形变的总量在增加,维持总变形量所需要的外力在减小,应力松弛速率加快,应力松弛极限降低。
图3所示为应力松弛极限与温度的关系。通过拟合该曲线,即可获得应力松弛极限与温度的经验公式,即:

式中:∞σ为应力松弛极限。
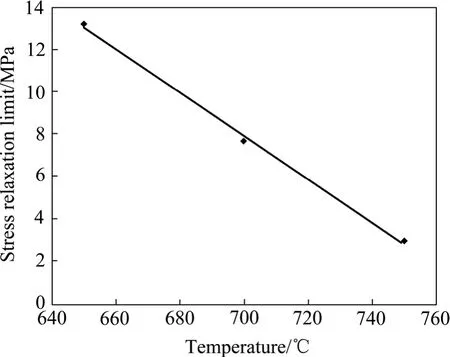
图3 应力松弛极限与温度的关系Fig. 3 Relationship between stress relaxation limit and temperature
图4所示为不同温度和初始应力0σ下Ti6Al4V合金的应力松弛曲线。由图4可知,温度相同时,初始应力分别为100和150 MPa时,其对应的应力松弛曲线均会趋向于各自的应力松弛极限,且初始应力较大时,最终的应力松弛极限较大,但是两者之间的差异并不是很大。温度为650 ℃时,两者的应力松弛极限相差6 MPa;700 ℃时相差5 MPa;750 ℃时仅相差1 MPa。
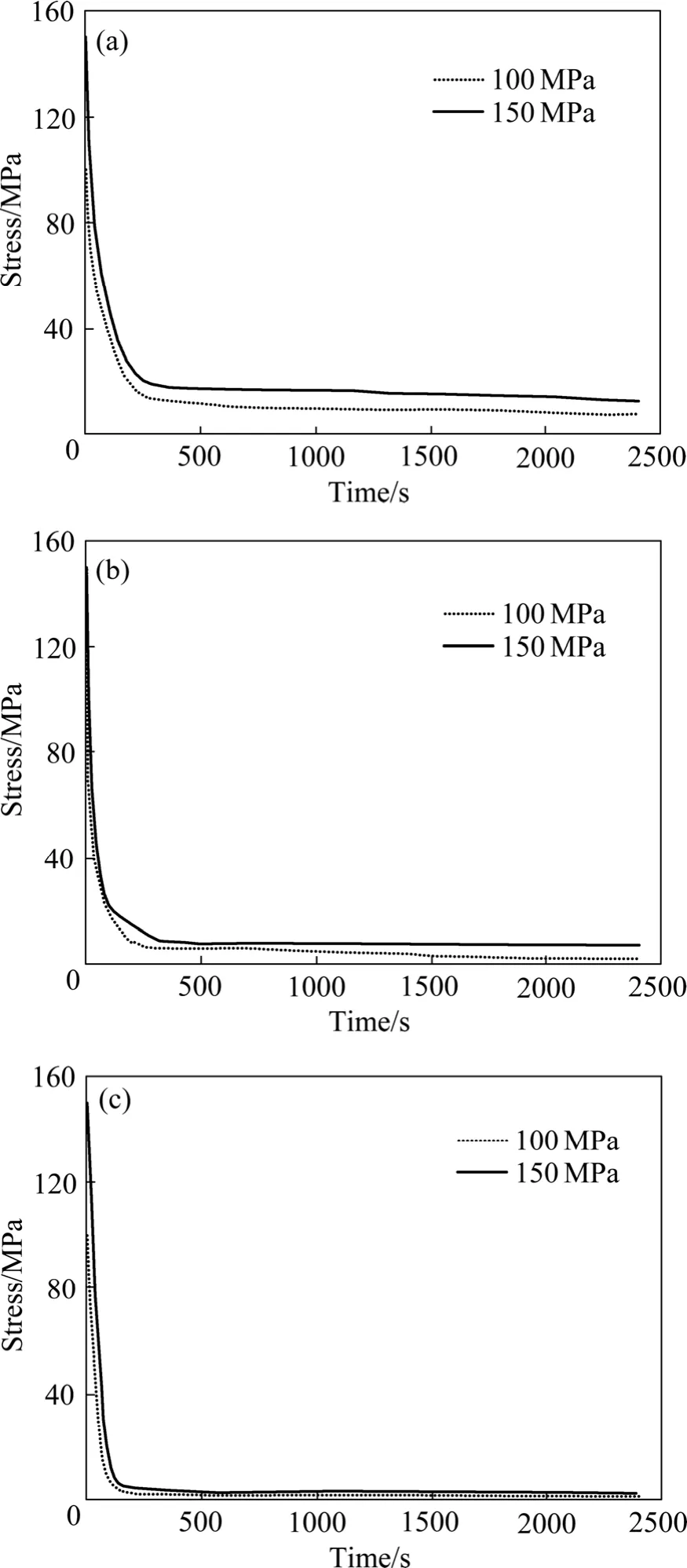
图4 不同温度和初始应力下Ti6Al4V合金的应力松弛曲线Fig. 4 Stress relaxation curves of Ti6Al4V alloy at different temperatures and initial stresses: (a) 650 ℃; (b) 700 ℃;(c) 750 ℃
图5所示为不同温度和预应变下Ti6Al4V合金的应力松弛曲线。由图5可知,温度相同条件下,预应变较大时,应力松弛极限较大,但是两者的差别不大,这说明预应变对应力松弛极限的影响较小。
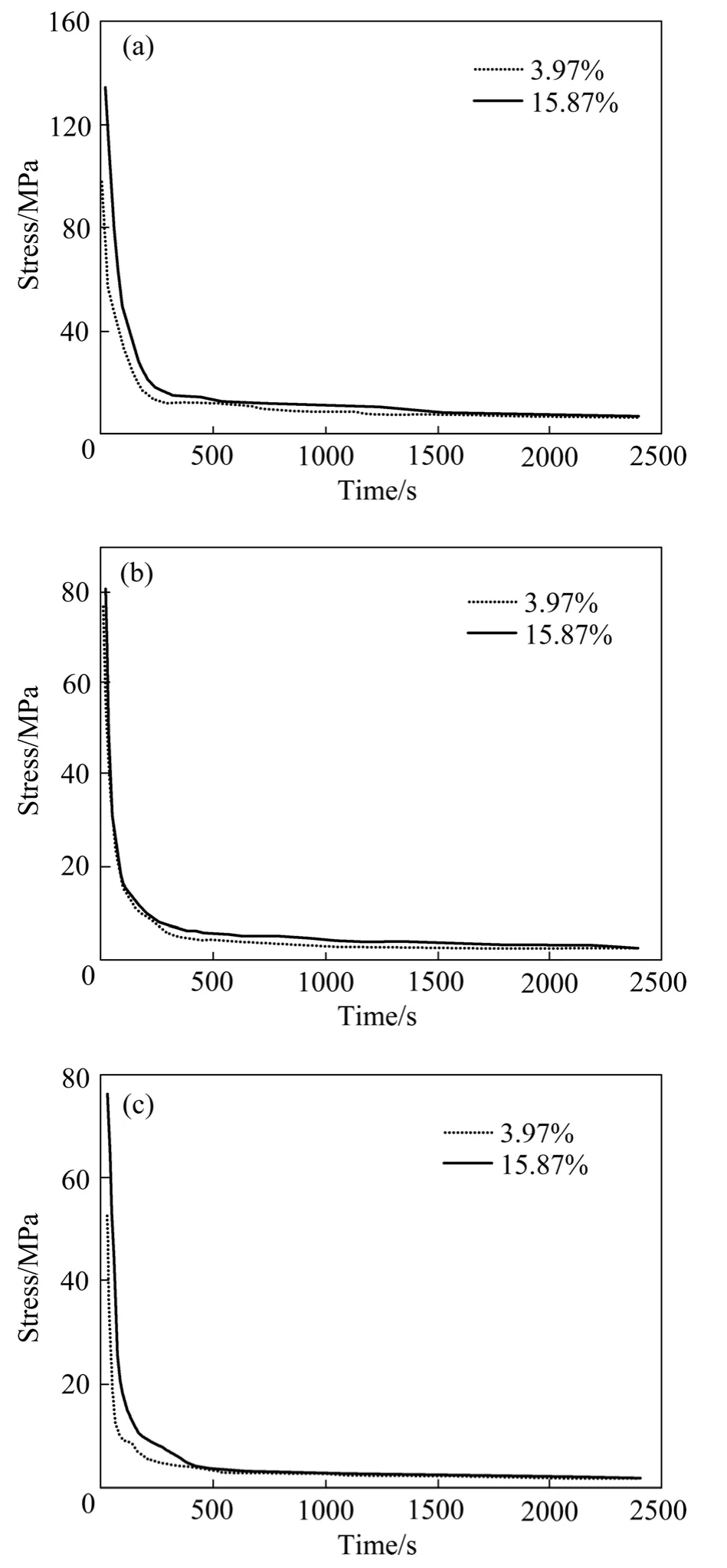
图5 不同温度和预应变下Ti6Al4V合金的应力松弛曲线Fig. 5 Stress relaxation curves of Ti6Al4V alloy at different temperatures and pre-strains: (a) 650 ℃; (b) 700 ℃; (c) 750 ℃
2.3 应力松弛曲线拟合
学者们在大量的试验基础上,提出了多种可用于描述金属材料应力松弛行为的经验公式,在此,将采用二次延迟函数来对Ti6Al4V合金的应力松弛曲线进行拟合[16]:

式中:σ为瞬时应力;∞σ为应力松弛极限;B、C、1τ、2τ均为常数。通过拟合试验数据,可得应力松弛方程。表2所列为不同条件下Ti6Al4V合金板材应力松弛方程的参数。
图6所示为700 ℃时两种预应变条件下拟合得到的曲线与试验数据的对比。图7所示为750 ℃时两种初始应力条件下拟合得到的曲线与试验数据的对比。由图6和7可以看出,二次延迟函数可以很好的拟合应力松弛曲线。
2.4 高温短时蠕变本构关系
在应力松弛过程中,蠕变应变速率与应力之间的关系对整个过程的研究有着至关重要的作用。
首先,对式(1)两边同时求导可得:

式中:creepε˙为塑性应变速率,即蠕变应变速率;E为弹性模量; t d/dσ 为应力松弛速率。
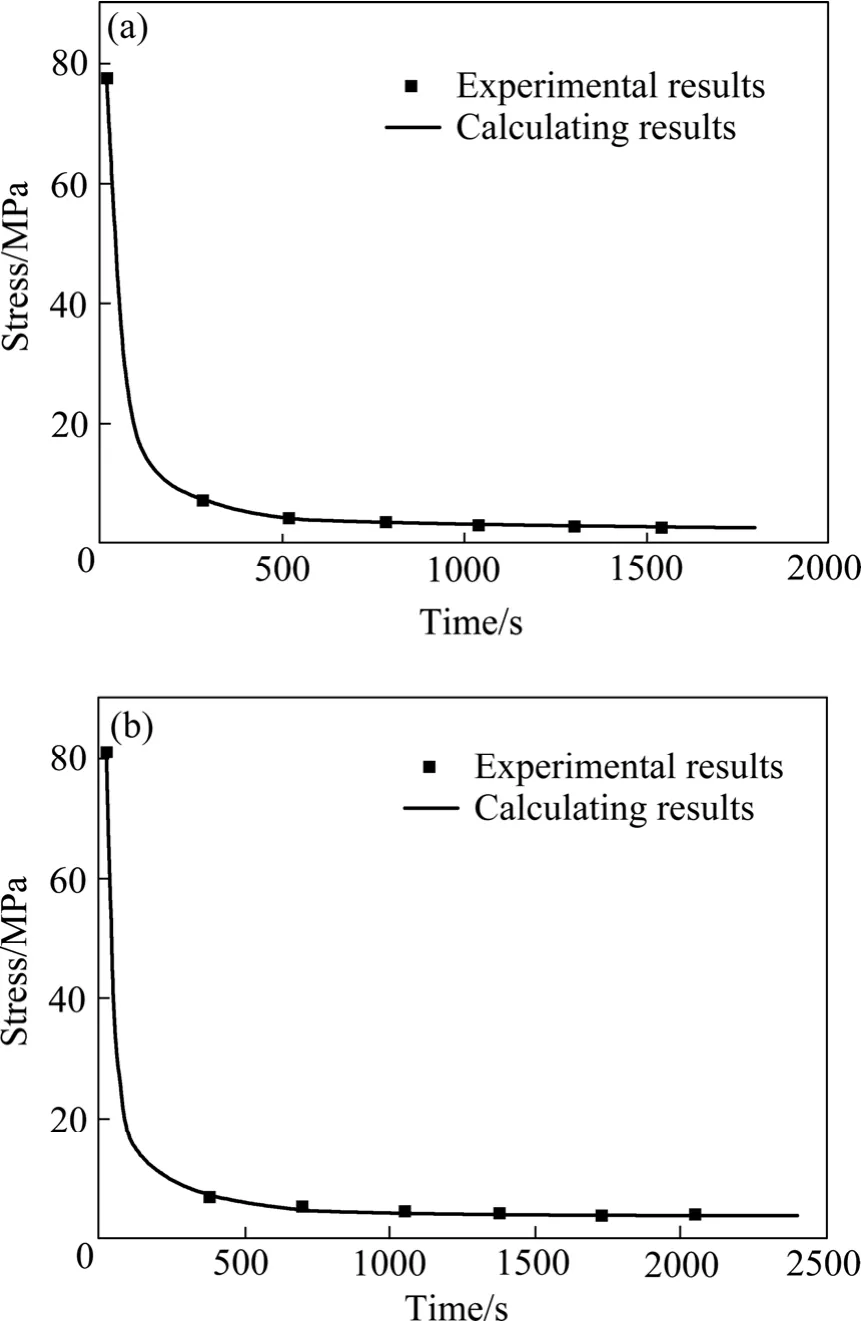
图6 700 ℃不同预应变下试验曲线与拟合曲线的对比Fig. 6 Comparison of experimental curves and fitting curves at different pre-strains and 700 ℃: (a) 3.97%; (b) 15.87%
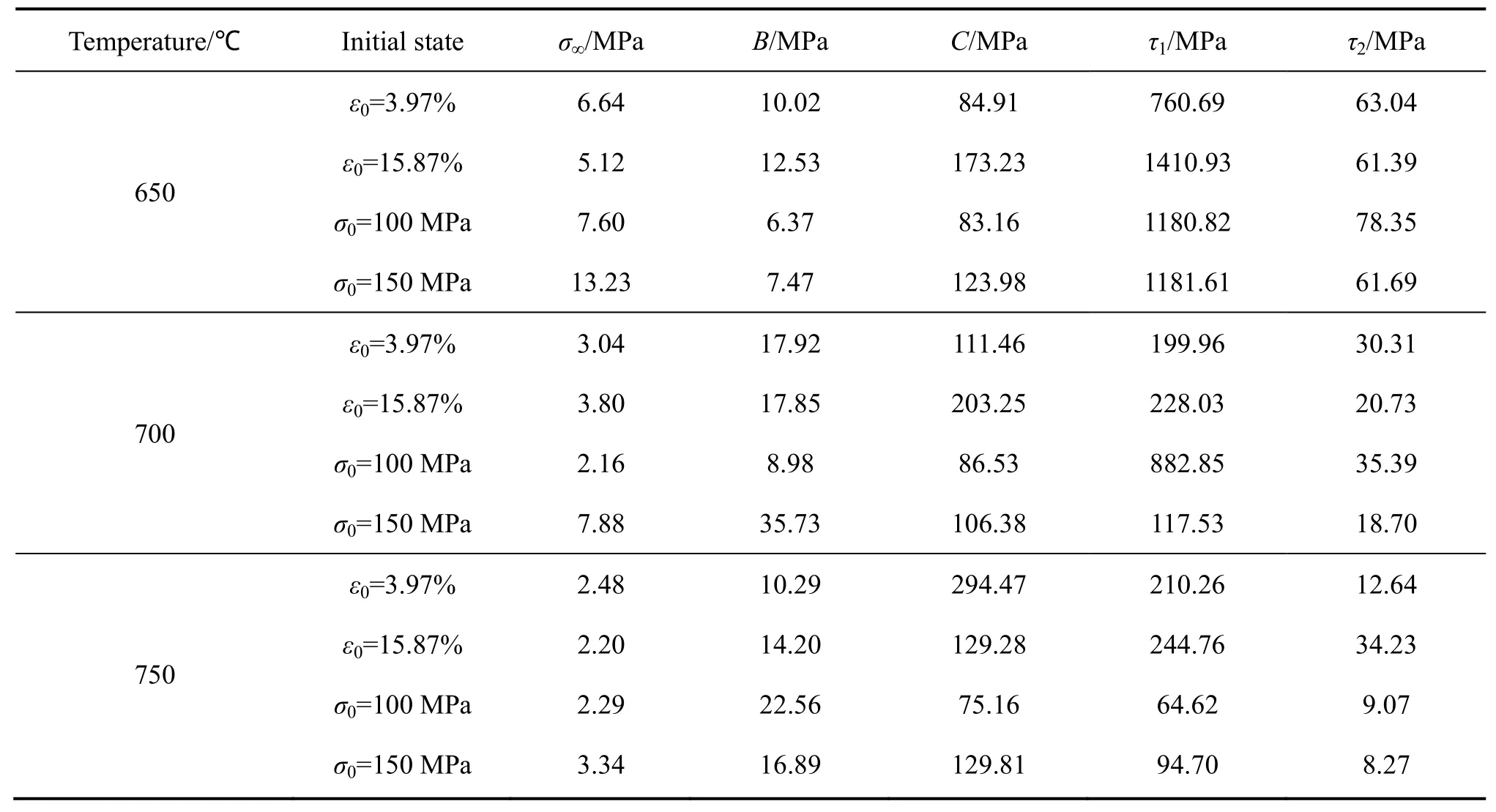
表2 Ti6Al4V合金板材在不同条件下的应力松弛方程参数Table 2 Stress relaxation equation parameters of Ti6Al4V alloy sheet under different conditions
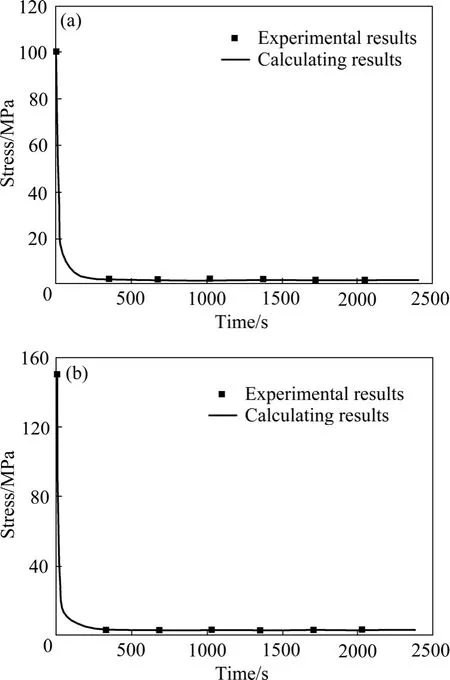
图7 750 ℃不同初始应力下试验曲线与拟合曲线的对比Fig. 7 Comparison of experimental curves and fitting curves at different initial stresses and 750 ℃: (a) σ0=100 MPa; (b)σ0=150 MPa
通过式(6),结合试验数据即可得到高温短时蠕变应变速率-应力曲线,结果如图8所示。
从图8可以看出,3种温度下的短时蠕变应变速率-应力曲线均可以分为两个区域,即低应力区域和高应力区域。由于幂指函数形式的蠕变本构模型适用于低应力条件下的蠕变行为,因此在低应力区域可以选择式(7)来描述Ti6Al4V合金高温短时蠕变过程[17]:
式中:creepε˙为蠕变应变速率;σ为应力;A为材料常数;n为应力指数。通过观察发现,在高应力区域,蠕变应变速率与应力呈线性关系。综上所述,可以建立如下的高温短时蠕变本构方程:

式中:A、D1、D2和n均为材料常数; σcritical为低应力区域与高应力区域的临界应力。
通过 OriginPro8.0对短时蠕变应变速率-应力曲线进行拟合,即可获得高温短时蠕变本构方程中各材料常数,如表3所列。
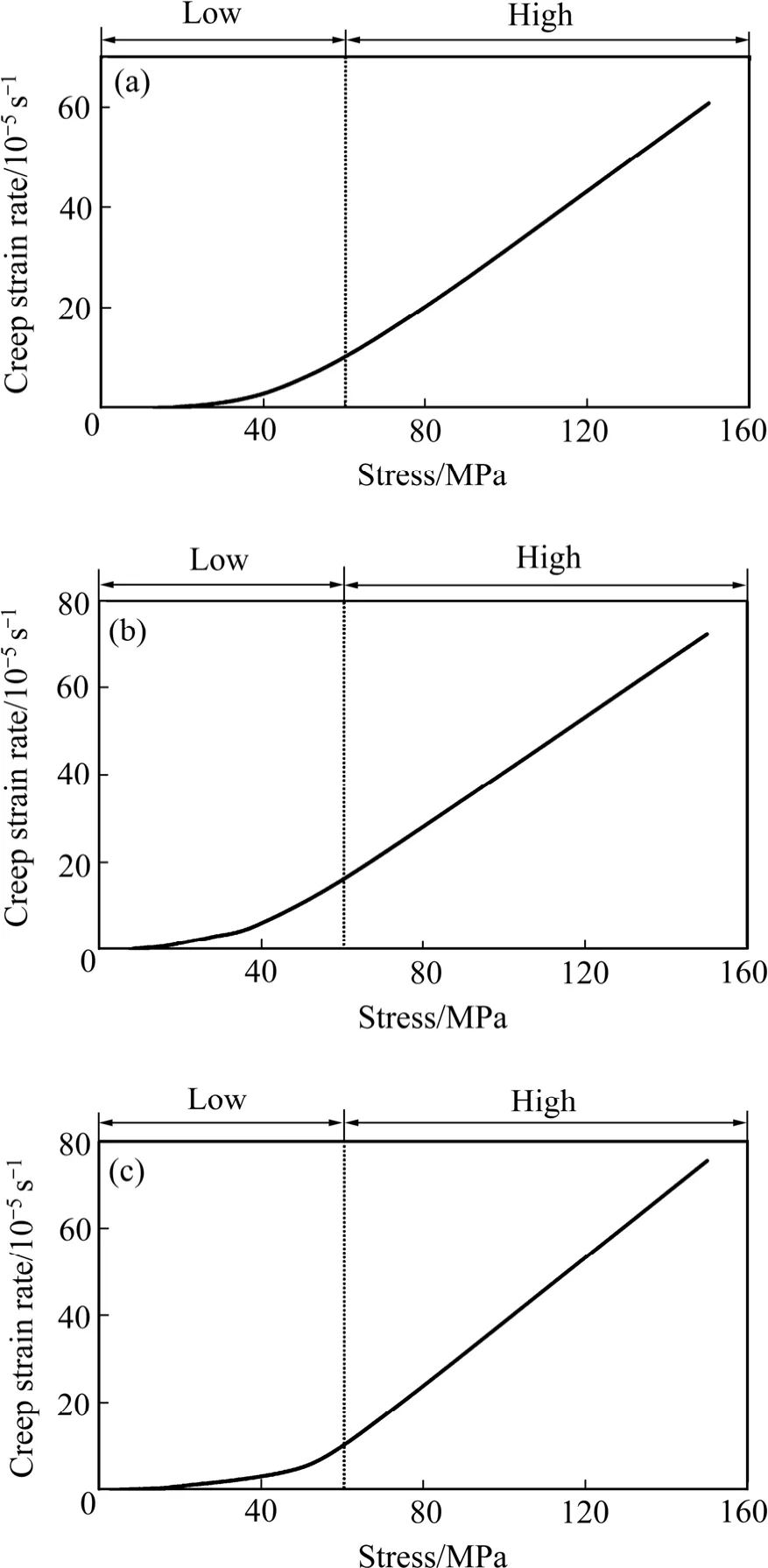
图 8 不同温度下 Ti6Al4V合金短时蠕变应变速率-应力曲线Fig. 8 Short-term creep strain rate-stress curves of Ti6Al4V alloy at different temperatures: (a) 650 ℃; (b) 700 ℃;(c) 750 ℃
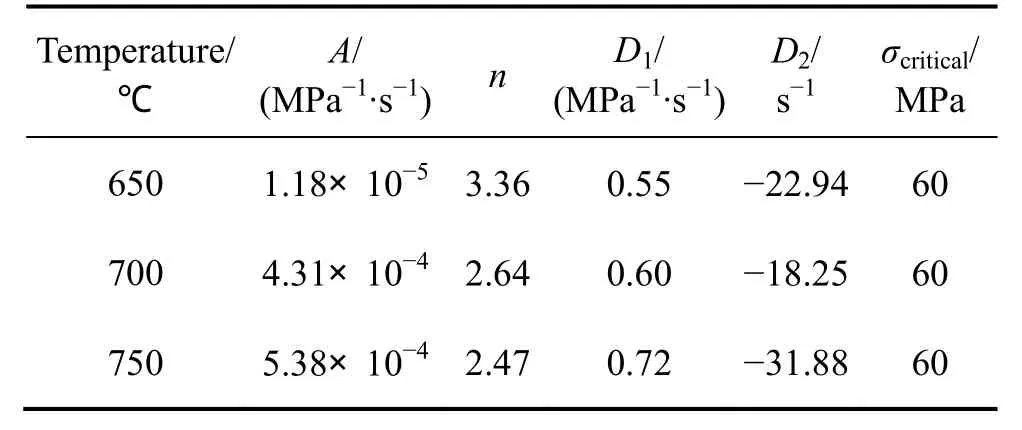
表3 高温短时蠕变本构方程材料常数Table 3 Material constants of short-term creep constitutive equations at high temperature
2.5 高温短时蠕变本构关系的验证
通过ABAQUS有限元软件建立了Ti6Al4V合金试样应力松弛的有限元模型,图9所示为设置有限元模型的载荷作用。
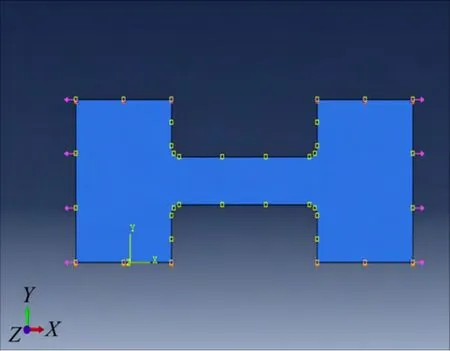
图9 Ti6Al4V合金有限元模型的载荷作用Fig. 9 Load of finite element model for Ti6Al4V alloy
图10所示为初始应力为150 MPa,在650、700和750 ℃温度条件下通过有限元模拟得到的曲线与试验曲线的对比。通过对比应力松弛过程的第一阶段和第二阶段可知,第二阶段的模拟结果较第一阶段而言与试验数据具有更高的吻合度,就总体而言,高温短时蠕变本构关系具有较高的可靠性。
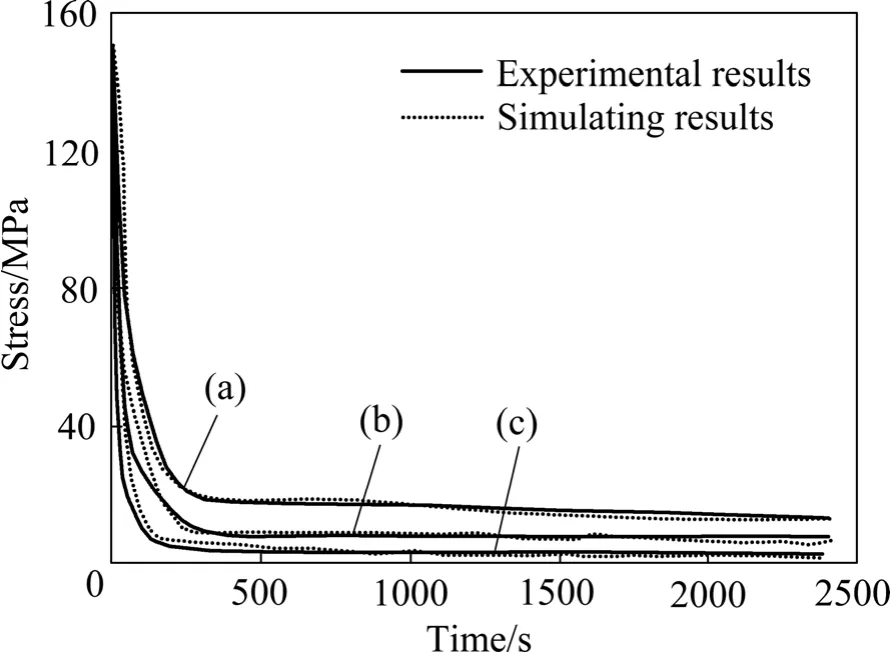
图10 不同温度下模拟应力松弛曲线与试验结果的对比Fig.10 Comparison of simulated stress relaxation curves and experimental results at different temperatures: (a) 650 ℃;(b) 700 ℃; (c) 750 ℃
3 结论
1) 在650~750 ℃温度范围内,Ti6Al4V合金板材的应力松弛分为两个阶段:第一个阶段为整个应力松弛过程的前250 s,应力急剧降低,但松弛速率随着时间的增加而逐渐减小;第二个阶段剩余应力的降低极为缓慢,经过2000 s后应力值基本不会再发生太大的变化,趋向于应力松弛极限。
2) 温度对 Ti6Al4V合金板材的应力松弛行为影响显著,应力松弛极限随着温度的升高而减小,松弛速率随着温度的升高而增加。初始应力和预应变越大,应力松弛极限越大,但是两者对应力松弛行为的影响不大。
3) Ti6Al4V合金板材在650~750 ℃温度范围内的应力松弛行为符合方程: σ =σ∞+Be-t/τ1+Ce-t/τ2。
4) 通过试验数据绘制出应力松弛曲线,并推导出Ti6Al4V合金板材在650~750 ℃温度范围内发生应力松弛时,短时蠕变应变速率与应力之间的关系。
5) 通过拟合短时蠕变应变速率-应力曲线,得到用于反映Ti6Al4V合金板材高温下应力松弛行为的短时蠕变本构关系,并得到本构方程中对应不同温度下的材料参数。
6) 将高温短时蠕变本构关系带入ABAQUS有限元软件中对Ti6Al4V合金的应力松弛行为进行模拟,模拟结果与试验所得到的应力松弛曲线具有很高的吻合度,证明了高温短时蠕变本构关系的可靠性。
[1] GOMAA E, MOHSEN M, TAHA A S. A study of annealing stage in Al-Mn (3004) alloy after cold rolling using positron annihilation lifetime technique and Vickers microhardness measurements[J]. Materials Science and Engineering A, 2003,362(S1/2): 274-279.
[2] 李桂荣, 李月明, 王芳芳, 王宏明. 脉冲强磁场处理对TC4钛合金显微组织及力学性能的影响[J]. 中国有色金属学报,2015, 25(2): 330-337.LI Gui-rong, LI Yue-ming, WANG Fang-fang, WANG Hong-ming. Effect of high pulsed magnetic field on microstructure and mechanical properties of TC4 titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2):330-337.
[3] 冯颖芳. 世界钛及钛合金的应用研究进展[J]. 世界有色金属,2012(4): 54-57.FENG Ying-fang. Application research progress of Ti and Ti alloys in the world[J]. World Nonferrous Metal, 2012(4): 54-57.
[4] 陈国清, 田唐永, 张新华, 李志强, 周文龙. Ti-6Al-4V钛合金陶瓷湿喷丸表面强化微观组织与疲劳性能[J]. 中国有色金属学报, 2013, 23(1): 122-127.CHEN Guo-qing, TIAN Tang-yong, ZHANG Xin-hua, LI Zhi-qiang, ZHOU Wen-long. Microstructure and fatigue properties of Ti-6Al-4V titanium alloy treated by wet shot peening of ceramic beeds[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(1): 122-127.
[5] WANG M W, ZHANG L W, PEI J B, LI C H, ZHANG F Y.Effect of temperature on vacuum hot bulge forming of BT20 titanium alloy cylindrical workpiece[J]. Transactions of Nonferrous Metals Society of China, 2007, 17(5): 957-962.
[6] IDEM K, PEDDIESON J. Simulation of the age forming process[J]. Journal of Manufacturing Science and Engineering,2005, 127(2): 165-172.
[7] 刘 坡, 宗影影, 郭 斌, 单德彬. 钛合金高温短时蠕变与应力松弛的关系研究[J]. 材料研究学报, 2014, 28(5): 339-345.LIU Po, ZONG Ying-ying, GUO Bin, SHAN De-bin. Relation between short-term creep and stress relaxation of titanium alloy at high temperature[J]. Chinese Journal of Materials Research,2014, 28(5): 339-345.
[8] HO K C, LIN J, DEAN T A. Modeling of springback in creep forming thick aluminum sheets[J]. International Journal of Plasticity, 2004, 20(4/5): 733-751.
[9] HO K C, LIN J, DEAN T A. Constitutive modelling of primary creep for age forming an aluminum alloy[J]. Journal of Materials Processing Technology, 2004, 153(32): 122-127.
[10] 陈缇萦. TC18钛合金的高温变形与蠕变行为研究[D]. 长沙:中南大学, 2012: 1-76.CHEN Ti-ying. Research on high temperature deformation and creep behavior of TC18[D]. Changsha: Central South University,2012: 1-76.
[11] 申发兰, 陈明和, 冯建超. TA15合金高温应力松弛和流变应力行为[J]. 宇航材料工艺, 2013, 43(3): 114-119.SHEN Fa-lan, CHEN Ming-he, FENG Jian-chao. Stress relaxation and flow stress of TA15 alloy at elevated temperature[J]. Aerospace Materials & Technology, 2013, 43(3):114-119.
[12] 李建伟. 细晶 TC21钛合金短时高温蠕变与应力松弛行为及机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 1-61.LI Jian-wei. Research on the behavior and mechanism of short-time high temperature creep and stress relaxation of fine grain TC21 titanium alloy[D]. Harbin: Harbin Institute of Technology, 2013: 1-61.
[13] SCHUH C, DUNAND D C. An overview of power-law creep in polycrystalline β-titanium[J]. Scripta Materialia, 2001, 45(12):1415-1421.
[14] 朱 智, 张立文, 顾森东. Hastelloy C-276合金应力松弛试验及蠕变本构方程[J]. 中国有色金属学报, 2012, 22(4):1063-1067.ZHU Zhi, ZHANG Li-wen, GU Sen-dong. Stress relaxation test of Hastelloy C-276 alloy and its creep constitutive equation[J].The Chinese Journal of Nonferrous Metals, 2012, 22(4):1063-1067.
[15] 刘 勇, 尹钟大, 朱景川. 温度、应力及晶粒度对TC4合金应力松驰性能的影响[J]. 稀有金属材料与工程, 2003, 32(8):643-646.LIU Yong, YIN Zhong-da, ZHU Jing-chuan. Effect of temperature, stress and grain size on stress relaxation in the alloy TC4[J]. Rare Metal Material and Engineering, 2003, 32(8):643-646.
[16] CHEN Chun-kui, Huang Yong-jian, WANG Yi-fan, WANG Kai-ning. Hot sizing of titanium workpieces and titanium alloy workpieces[J]. Materials Science and Technology, 1985, 4(2):89-100.
[17] 汪 军. 钛合金的蠕变行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2008: 1-55.WANG Jun. A study on creep behavior of titanium alloy[D].Harbin: Harbin Institute of Technology, 2008: 1-55.
