废杂铜精炼过程中动态多元多相平衡热力学模型
2015-03-26黄金堤童长仁李明周徐志峰
黄金堤 ,李 静,童长仁,李明周, ,徐志峰
(1. 江西理工大学 建筑与资源工程系,南昌 330013;2. 中南大学 冶金与环境学院,长沙 410083;3. 江西理工大学 冶金与化学工程学院,赣州 341000)
废杂铜具有良好的再生利用特性,相对于传统铜精矿冶炼,废杂铜再生每吨可节能80%~90%,再生铜的循环利用已成为世界铜工业的重要组成部分[1]。GÓMEZ等[2]指出从1966年到 2005年,世界可再生废杂铜可利用量增加了 300%,但再生铜的利用率仅上升了35%,大量的废杂铜仍未能有效利用。中国自2006年起已成为世界最大的铜消费国和生产国[3],近10年来,发达国家再生铜产量占精炼铜产量的比例超过50%,而目前我国只占到30%,“十二五”规划目标指出,我国将加大再生铜比例,争取达到 40%[4]。因此,再生铜的回收利用不仅是目前缓解我国铜资源短缺的主要手段,也是铜冶炼行业节能减排的重要措施。
火法精炼处理的废杂铜占再生铜产量的 80%以上,废杂铜火法精炼的主要工艺有FRHC废杂铜精炼工艺、反射炉工艺、倾动炉工艺、NGL炉工艺、卡尔多炉工艺和ISA/Ausmelt工艺[5-7]。其中,倾动炉具有自动化程度高、节能和安全环保的特点,多用来处理含铜在90%以上的废杂铜,是当前处理高品位废杂铜的主要炉型[6]。
废杂铜精炼过程是一个高温、多元、多相的复杂反应过程,传统实验检测手段难以研究其物理化学过程。目前借助计算机模拟技术[8],使用多相平衡计算模型对高温冶炼过程进行的热力学研究,主要集中在铜、铅的硫化精矿的熔炼过程[9-12],而对于废杂铜的多元多相平衡研究未见报道。
多相平衡计算的主流算法有化学平衡常数法[13]和最小吉布斯函数法[14],两者都是基于自由能最小原理,但是平衡条件的计算方式有所区别。前者需要预先知道体系的组分数、相态和具体反应等,其通用性较差;后者无需确定体系化学反应方程,通用性较强。最小吉布斯函数法包括RAND法、NASA法、Wolfe法等[8,15-18],其中RAND法应用最为广泛。
本文作者基于吉布斯最小自由能原理[16]的RAND算法,建立基于时间离散的倾动炉杂铜精炼过程的动态多元多相平衡热力学模型,模拟计算各周期的各相组分含量,并结合实际生产数据对模型进行验证,为倾动炉杂铜精炼过程的反应机理、杂质分配规律以及工艺参数优化提供一定的理论依据。
1 数学模型计算原理
1.1 数学模型基本假设
1) 倾动炉炉内熔体在单位时间内混合均匀;
2) 倾动炉在单位时间微元内温度、压力恒定,反应达到平衡状态;
3) 体系中烟气视为理想气体;
4) 倒渣过程中粗铜相与炉渣相交接处的部分粗铜随着炉渣排出,其值为固定值。
1.2 最小自由能原理
最小自由能原理是指在恒温恒压下,化学反应沿着吉布斯自由能减小的方向进行。当吉布斯自由能达到最小值时,体系就达到了平衡。由热力学第二定律可知,对于一个在恒温恒压、无非体积膨胀功的体系有:
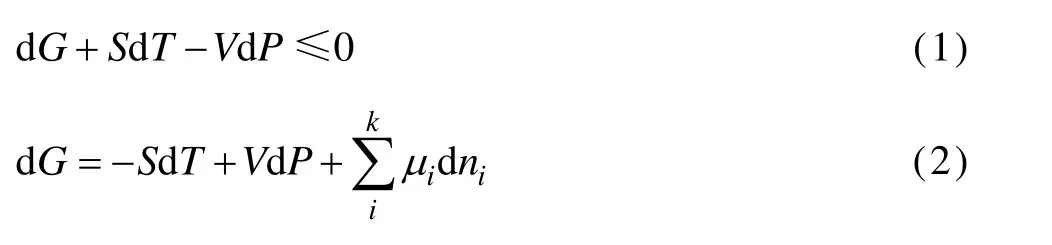
式中:G为吉布斯自由能;T为温度;S为系统的熵;V为系统体积;µi为第i组分的化学势;ni为第i组分的摩尔数;P为体系的相数;k为组分数。
由式(1)和式(2)得

式(4)为多相多组分反应体系是否达到平衡的判据,当体系处于平衡状态时,等号成立;当体系处于非平衡状态时,小于号成立。即体系总是向着吉布斯自由能减小的方向变化,直到吉布斯自由能达到最小时体系达到平衡。
系统总吉布斯自由能可表示为
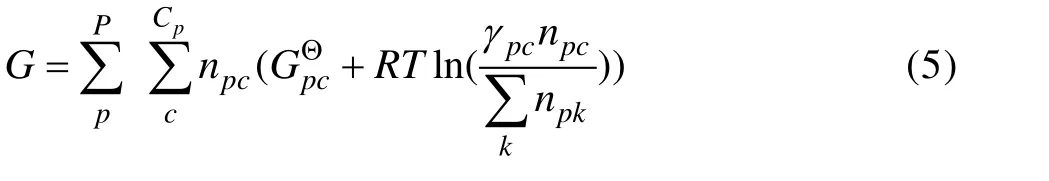
式中:npc为第p相中c组分的摩尔数;为第p相中 c组分为纯物质的标准生成吉布斯自由能;γpc为第p相中c组分的活度系数;npk为p相中的k组份摩尔数;R为气体普适常数。
将吉布斯自由能 G在n(m)处用泰勒公式二阶展开:

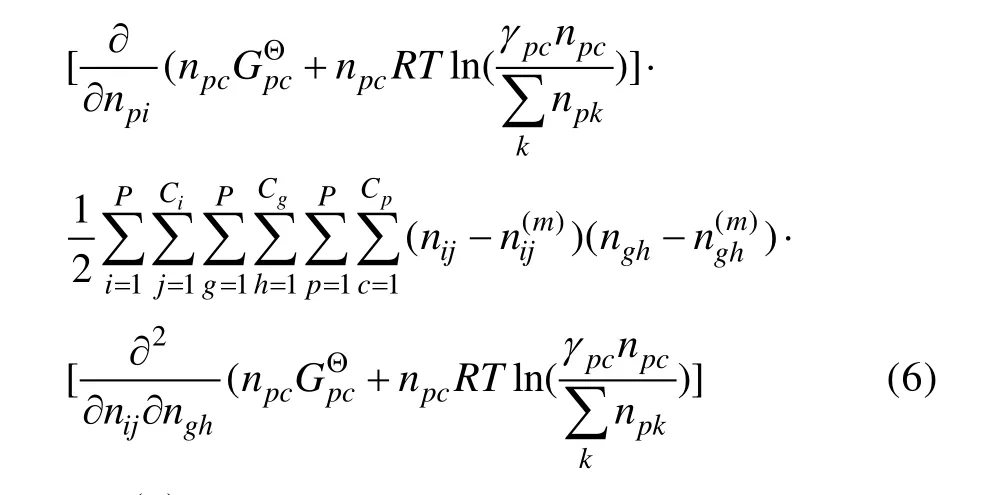
结合质量守恒有
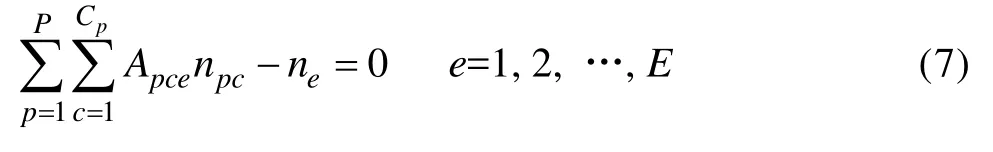
式中:Apce为第p相中c组分分子式中e原子的个数;ne为体系中e原子的总摩尔分数;E为体系中元素种类数。
按拉格朗日因子法,构造L函数式,将有约束条件的极值问题转化为无约束条件的极值问题。
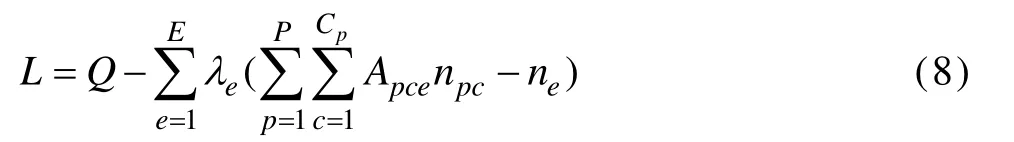
式中:λe为拉格朗日因子。
按极值必要条件,将L函数对各npc及λe分别求偏导,并令各偏导等于0,可得式(9):
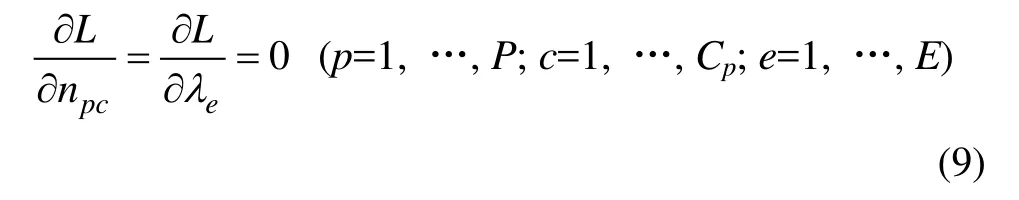
采用迭代法求解式(9),可得平衡时各相各组分摩尔数。同时,由于方程中各活度系数γpc并非一定为常数,通常与组成有关,算法采用多层迭代计算方法,先迭代收敛npc后迭代求解γpc。
1.3 机械夹杂修正
在生产过程中,在粗铜与炉渣相间存在相互机械夹杂,所以基于热力学平衡的计算结果通常应进一步加以修正。本模型采用机械夹杂方程进行修正。

式中:mcr为进入渣中的粗铜质量;msl为炉渣的表观质量。

式中:msc为进入粗铜中的渣质量;mca为粗铜的表观质量。

式中:wca为M在粗铜中的平衡计算含量;wsl为M在渣中的平衡计算含量。
将式(10)代入式(12)得

式(13)和(15)即为 SHIMPO 等[19]和 NAGAMORI等[20]的机械夹杂修正方程。
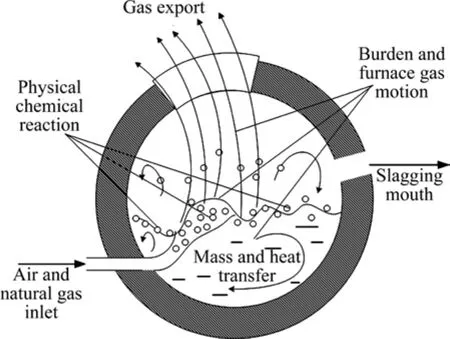
图1 倾动炉杂铜精炼示意图Fig. 1 Schematic diagram of scrap copper refined by tilting furnace
2 倾动炉废杂铜精炼动态数学模型
2.1 倾动炉精炼流程
图1所示为倾动炉杂铜精炼过程的示意图。倾动炉杂铜精炼过程是间歇式的周期性作业,按冶炼的过程可分为4个阶段:加料熔化期、氧化造渣期、还原期、浇铸期。
精炼的第一阶段,主要进行的是粗铜、石英砂的熔化过程;精炼的第二阶段,通过风口向炉内鼓入空气来实现粗铜的氧化。由于大量上升的小气泡与熔体之间接触面积很大,加快了杂质的氧化反应。粗铜中的MeS、Me与鼓入空气中的氧发生强烈的氧化反应,生成MeO和SO2气体。其中FeS与氧气及加入的石英熔剂反应造渣,使粗铜中铜含量逐渐升高。由于粗铜与炉渣相互溶解度很小且密度不同,所以炉内物相分成两层,上层炉渣被定期排出。这个阶段持续到粗铜中Cu含量为99%以上、O含量大于0.5%时结束;在精炼的第三阶段,鼓入天然气中的 H2与 Cu2O发生强烈的还原反应,生成金属Cu和H2O,直到生成的粗铜Cu含量大于等于99.5%时精炼的第三阶段结束。最后炉体转动将铜水倒出,铜水经溜槽连续流入中间包,中间包的铜水再通过浇铸包进行定量浇铸。
2.2 动态多相平衡模型
设杂铜精炼过程在t~(t+Δt)时间段,根据能量守恒定律有
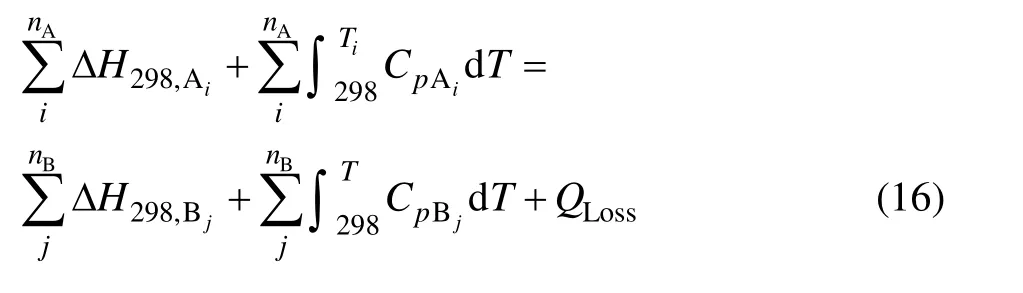
式中:Ai为反应物;Ti为反应物Ai的初始温度;Bj为生成物;T为生成物Bj的温度;nA为反应物数量;nB为生成物数量;H为焓值;Cp为热容;QLoss为热损失量。
杂铜精炼过程的传热行为非常复杂,包括熔体、烟气、空气与炉壳和炉衬、炉壳外壁与外部环境之间的对流、扩散、辐射等传热方式,为简化模型,指定热损失量QLoss为恒定值。
在倾动炉内,反应物不断进入系统,产出物不断离开系统,炉内是一个非平衡态反应过程。同时由于火法冶金过程反应速度较快,可假定系统在微小时间单元内物料达到平衡状态[19]。按式(16)进行炉内温度计算,该动态多相平衡模型的原则流程见图2。
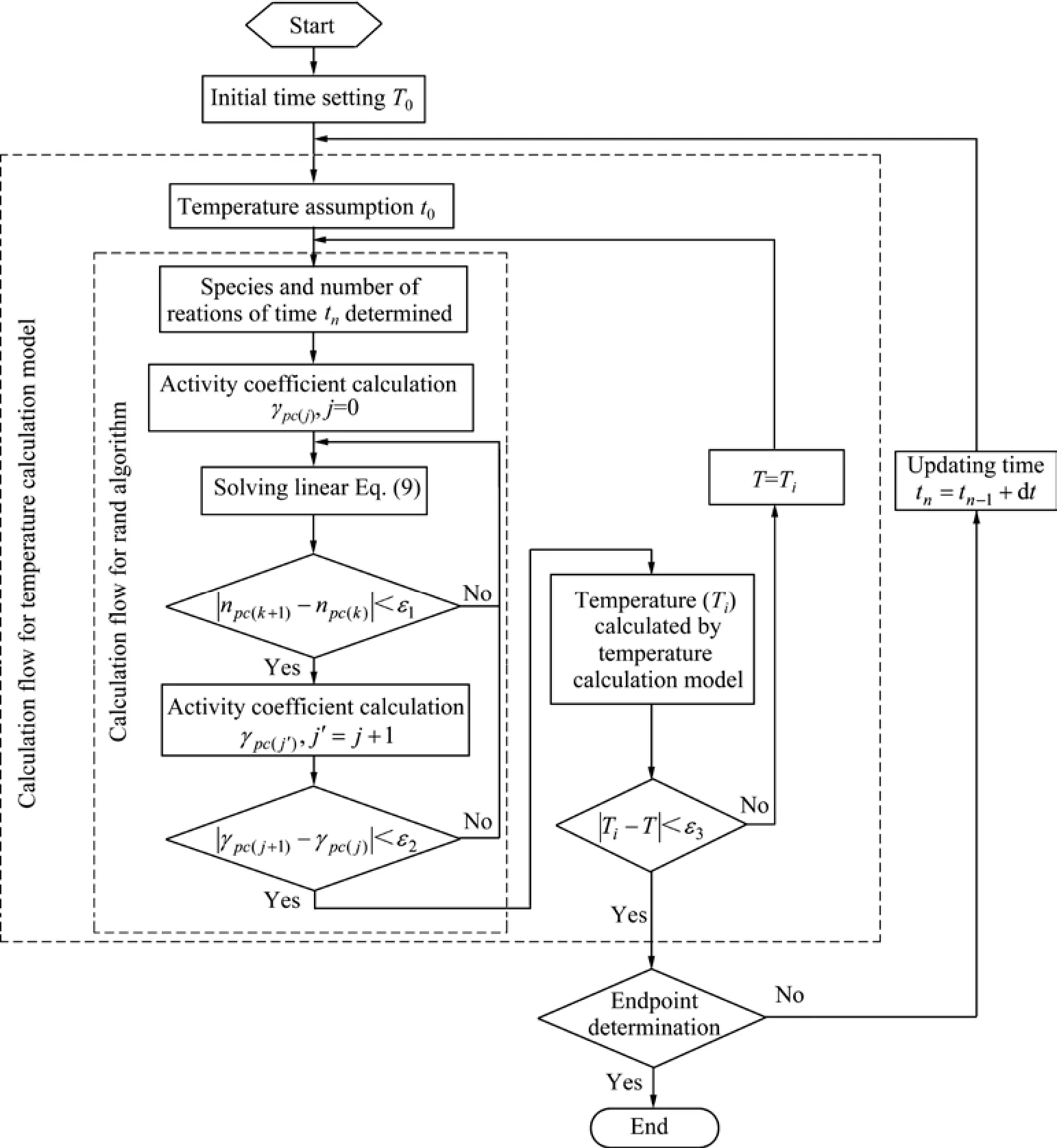
图2 动态化学平衡模型计算流程图Fig. 2 Calculation flow chart of dynamic chemical equilibrium model
3 基本数据
3.1 体系各相组分
废杂铜精炼过程投入的各类物料主要有杂铜、石英熔剂、石灰石、苏打、空气、工业氧气、天然气、重油。杂铜主要有铜箔、粗铜、铜管、阴极铜、紫杂铜、铜块(条)、阳极板、杂铜、废阳极板、残极、包底、冷铜、日常废板、其它特殊物料等。
各类物料涉及的元素众多,包括Cu、S、Fe、Si、Pb、Ca、Mg、As、Sb、Bi、Au、Ag、O、N、C、H等,杂铜精炼过程可视为粗铜、炉渣和烟气三相平衡体系[8,11,21-22],各相组成分别为
1) 炉渣相:FeO、SiO2、Fe3O4、Cu2O、PbO、As2O3、Sb2O3、Bi2O3、NiO、SnO;
2) 烟气相:SO2、SO、O2、N2、S2、CO、CO2、H2、H2O、Pb、PbO、AsO、As2、SbO、SbS、Sb、BiO、SnO;
3) 粗铜相:Cu、Cu2S、Cu2O、Fe、FeS、FeO、Pb、As、Sb、Sn、Bi、Ni。
3.2 相关热力学数据
根据式(17)计算吉布斯自由能,由 Metcal desk v5.54[23]获取相关热力学数据,具体数值见表1。炉内炉渣及粗铜相各物质相关活度系数见表2和3。
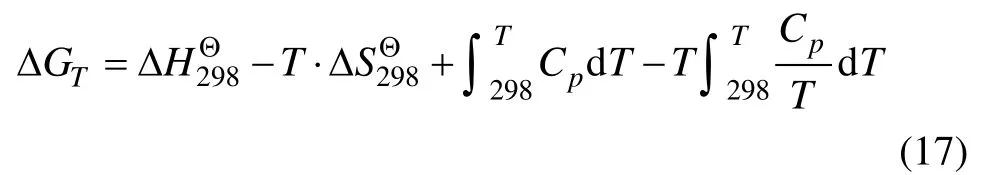
表 2与 3中的xFe3O4、xSiO2、xCu2O为炉渣中Fe3O4、SiO2、Cu2O 的摩尔分数,pO2为氧分压,烟气相活度均为1。
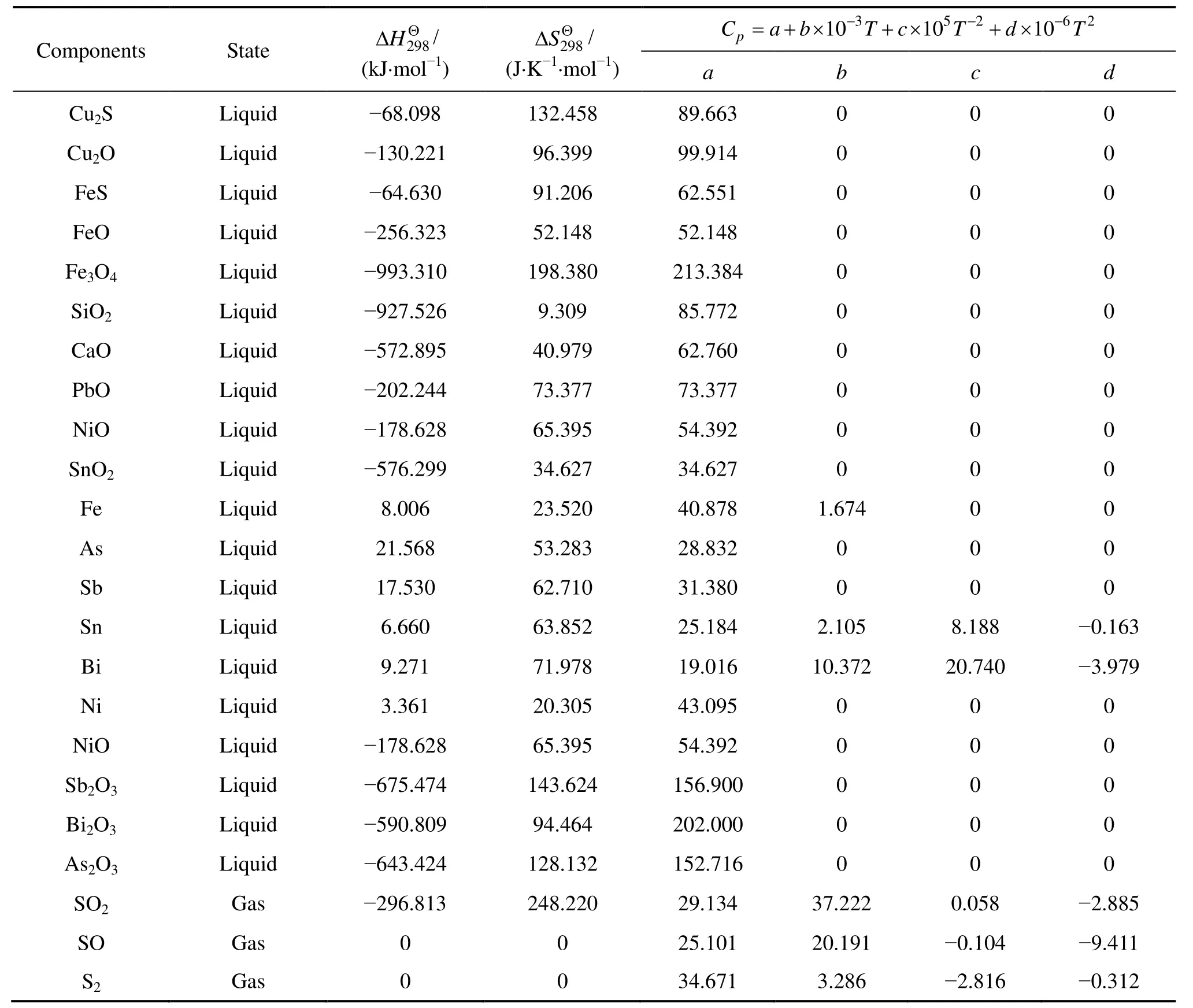
表1 组分的热力学参数[23-24]Table 1 Thermodynamic parameters of components[23-24]
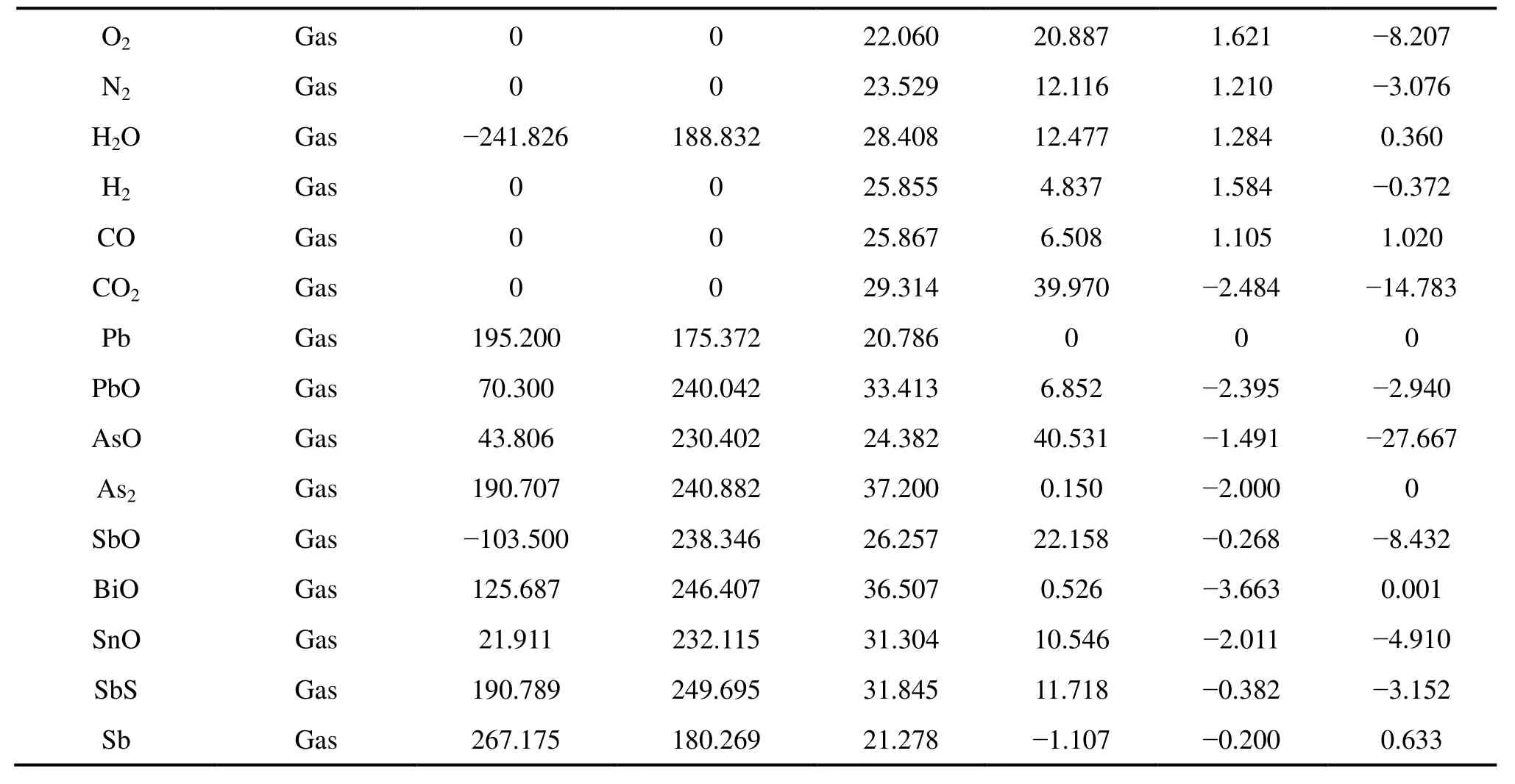
续表1
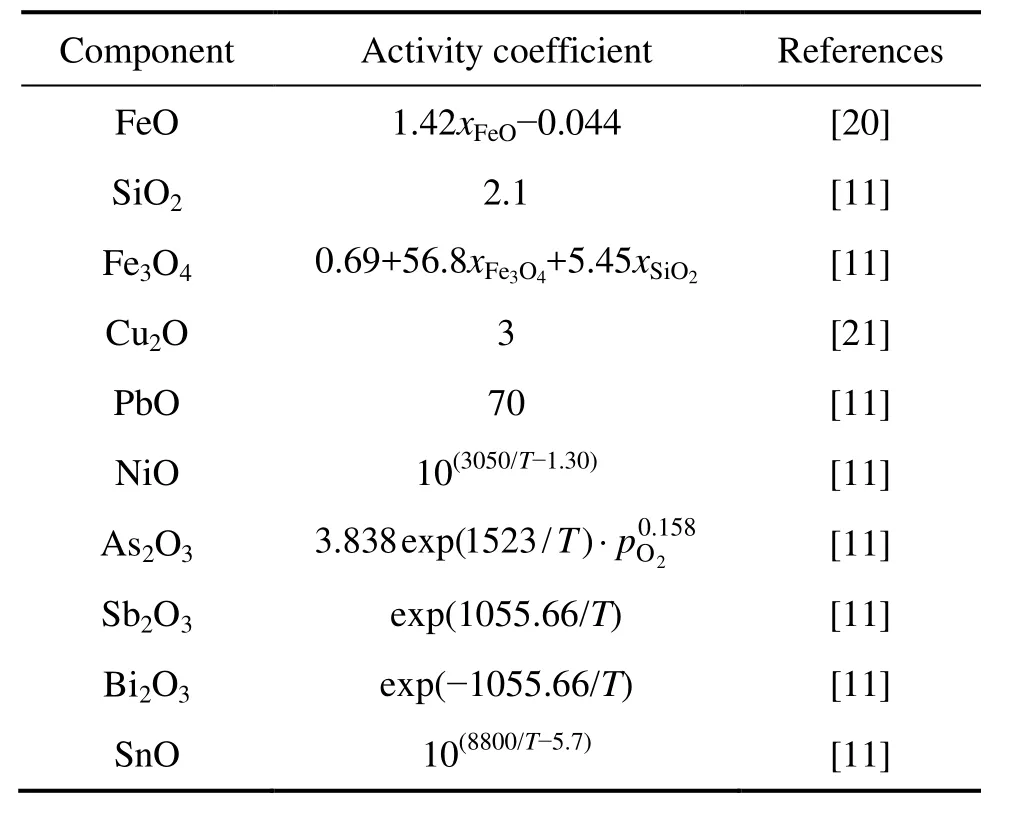
表2 炉渣中各组分的活度系数[11, 20-21]Table 2 Activity coefficient of components in slag[11, 20-21]

表3 铜中各组元的活度系数[11, 20-22]Table 3 Activity coefficient of components in blister copper[11, 20-22]
4 模型验证与应用
4.1 生产数据采集及分析
生产试验数据来源于某铜冶炼厂 2012年的 246号炉的样品,冶炼工艺技术参数见表 4。对倾动炉冶炼过程中的熔化期、氧化期及还原期各期终点进行取样分析,采用电感耦合等离子体原子发射光谱法(ICP-AES)分析粗铜、炉渣的组成,具体数据见表5。
4.2 模型验证
入炉熔化废杂铜(干基)的总量为399.0 t,在熔化过程结束,进入氧化造渣期前,取样检测样品中各元素的含量,结果见表6。
采用建立的动态多元多相化学平衡模型计算倾动炉杂铜精炼生产实践状态下的各周期的各相组分含量,操作工艺条件见表7,模拟计算结果见表8和9,其中氧化造渣期的计算需按照式(13)和(15)进行夹杂修正。
检测氧化期和还原期各期终点样品,将测量的质量分数值与模拟计算值进行比较分析,分析结果见表10和11。对氧化期炉渣终点样品中Cu及Fe含量进行检测,将测量的质量分数与模拟计算值进行比较,结果见表12。

表4 倾动炉冶炼工艺技术参数Table 4 Smelting process technical parameters of tilting furnace

表5 生产数据Table 5 Production data

表6 入炉熔化杂铜的平均组分含量Table 6 Average component content of initial scrap copper (mass fraction, %)
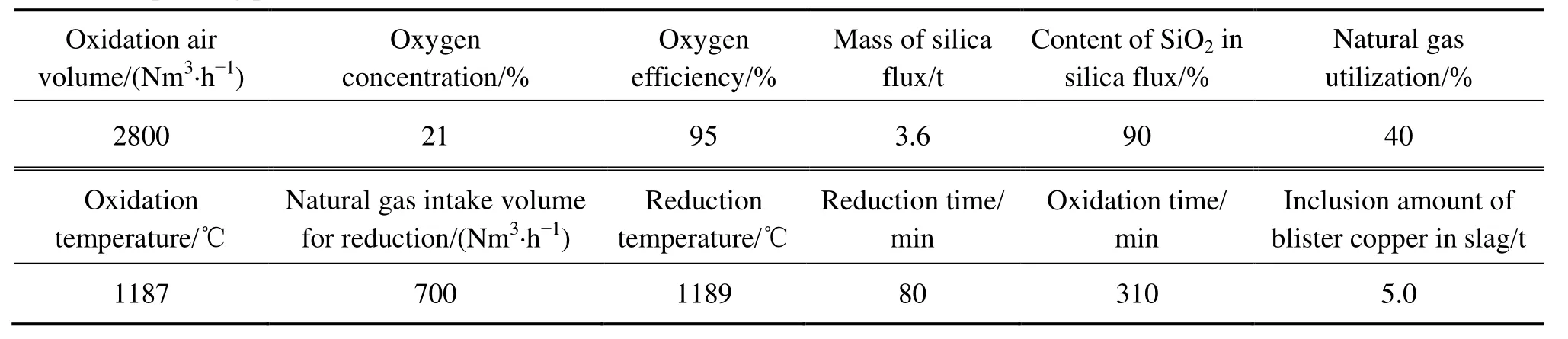
表7 操作工艺条件Table 7 Operating process conditions

表8 氧化造渣期仿真计算各相元素组成Table 8 Simulating elemental composition of oxidation period
由表10可知,氧化造渣期粗铜相中Cu质量分数的绝对误差为0.050%,相对误差为0.050%;O质量分数的绝对误差仅为 0.012%,相对误差为 2.638%。由表11可知,还原期粗铜相中Cu质量分数的绝对误差为0.042%,相对误差为0.042%;O质量分数的绝对误差仅为0.006%,相对误差为4.267%。由表12可知,炉渣相中Cu、Fe含量绝对误差分别为1.052%、0.504%,相对误差分别为2.782%、5.143%。对于杂质而言,相对误差较大的为Sn、Ni。造成这些偏差的主要原因如下:1) 由于部分粗铜未熔化及表面存在的部分渣相,测量的初始入炉物料成分存在偏差;2) 倾动炉炉内温度存在不均匀的特征,炉内上部区域由于有重油喷嘴进行加热,液面上方的区域温度高达1350 ℃,而整体的粗铜温度仅1150~1200 ℃;3) 模型假定系统每个周期均处于一个恒温过程,然而实际上熔化及造渣过程的温度处于动态变化状态;4) 实际生产过程中加入了铜熔剂除Sn。
采用建立的动态多元多相化学平衡模型分析了氧化造渣期和还原期的粗铜相中Cu2S、Cu2O以及烟气相中 SO2的质量分数变化趋势,结果见图 3。由图 3可知,在氧化造渣期,粗铜相中的 Cu2O呈现快速递增的趋势,Cu2S呈现迅速下降的趋势,这是由于在氧化初期,主要发生的反应为 MeS+O2→MeO+SO2及Cu2S+O2→Cu2O+SO2,随着Fe等杂质优先氧化造渣,Cu2S也逐渐被氧化形成Cu2O。同时,在氧化造渣期的烟气相中,SO2的质量分数呈现先递增后下降的趋势,这是由于在氧化初期,氧气主要用于Fe等杂质金属硫化物的优先氧化,随着这些杂质被逐渐氧化并进入渣相,粗铜中 Cu2S才开始与氧气反应,导致烟气相中二氧化硫的质量分数不断升高,但是当硫化物被氧化到一定程度进入氧化中后期时,粗铜相中 Cu2S含量逐渐降低,烟气相中SO2的质量分数也随之迅速下降。在还原期主要进行的反应为,该过程表现为Cu2O不断被还原并且SO2形成量极少,因此,还原期中,Cu2O的质量分数和SO2的质量分数呈现下降趋势。

表9 还原期仿真计算各相元素Table 9 Simulating elemental composition at reduction period
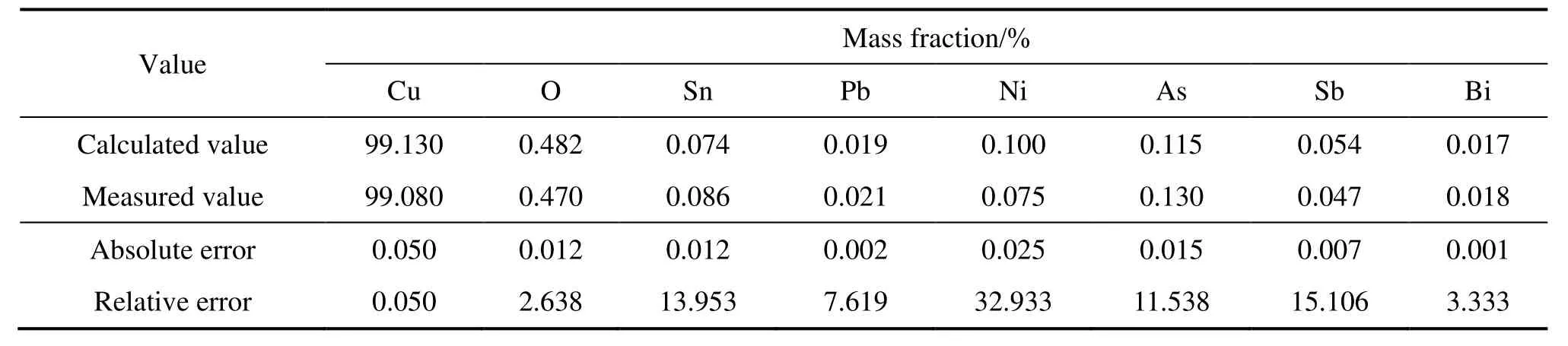
表10 氧化期粗铜相仿真值及生产试验结果Table 10 Simulation value and production test results of blister copper at oxidation period

表11 还原期粗铜相仿真值及生产试验结果Table 11 Simulation value and production test results of blister copper at reduction period

表12 炉渣相仿真值及生产试验结果Table 12 Simulation value and production test results of slag

图3 氧化造渣期和还原期粗铜相中Cu2S、Cu2O以及烟气相中SO2质量分数的变化趋势Fig. 3 Changing trend of mass fraction of Cu2S,Cu2O in blister copper and SO2 in gas phase smoke during oxidation and reduction periods
以上分析表明,建立的模型基本能够反映倾动炉杂铜精炼的生产实践过程,可作为分析倾动炉杂铜精炼过程物理化学过程的有效工具。
5 结论和讨论
1) 模拟值与实际值相比,氧化造渣期粗铜相中Cu质量分数的绝对误差为 0.050%,相对误差为0.050%;O质量分数的绝对误差为0.012%,相对误差为2.638%。还原期粗铜相中Cu质量分数的绝对误差为0.042%,相对误差为0.042%;O质量分数的绝对误差仅为0.006%,相对误差为4.267%。炉渣相中Cu、Fe含量绝对误差分别为 1.052%、0.504%,相对误差分别为2.782%、5.143%。
2) 模拟结果与生产试验数据较吻合,表明了基于吉布斯最小自由能原理,建立的基于时间离散的动态多元多相平衡热力学模型能够正确反映生产实际情况。该模型可作为分析倾动炉杂铜精炼过程物理化学行为的有效工具。
3) 受初始入炉废杂铜成分测量误差、模型的假设条件等因素的影响,粗铜中的 Sn、Pb、Ni、As、Sb含量的仿真值与实际测量值存在一定的偏差,但基本能够反映倾动炉杂铜精炼过程的各相杂质分布情况,可为倾动炉杂铜精炼中杂质分配规律的研究提供一定的理论依据。
[1] 李英道, 叶凌箭, 宋执环. 废杂铜冶炼过程子空间预测控制器的设计[J]. 江南大学学报(自然科学版), 2012(4): 385-390.LI Ying-dao, YE Ling-jian, SONG Zhi-huan. Design of subspace predictive controller in scrap copper smelting[J]. Joural of Jiangnan University (Natural Science Edition), 2012(4):385-390.
[2] GÓMEZ F, GUZMÁN J I, TILTON J E. Copper recycling and scrap availability[J]. Resources Policy, 2007, 32(4): 183-190.
[3] 周明文. 我国废杂铜工业的现状与发展趋势[J]. 有色冶金设计与研究, 2010, 31(6): 29-32.ZHOU Ming-wen. Present status and development trend of scrap cooper industry in China[J]. Nonferrous Metals Engineering &Research, 2010, 31(6): 29-32.
[4] 姚素平. 中国再生铜冶炼技术现状与发展趋势[J]. 中国有色金属, 2012(2): 40-41.YAO Su-ping. Present status and development trend of secondary copper smelting technology in China[J]. Chinese Journal of Nonferrous Metals, 2012(2): 40-41.
[5] AGHAZADEH M, ZAKERI A, BAFGHI M S. Modeling and optimization of surface quality of copper deposits recovered from brass scrap by direct electrowinning[J]. Hydrometallurgy,2012, 111/112: 103-108.
[6] 王 冲, 杨坤彬, 华宏全. 废杂铜回收利用工艺技术现状及展望[J]. 再生资源与循环经济, 2011, 4(8): 28-32.WANG Chong, YANG Kun-bin, HUA Hong-quan. Current status and prospect of recovery and utilization process for copper scrap[J]. Recyclable Resources and Circular Economy, 2011,4(8): 28-32.
[7] DECKERS J, HANSEN J. Tilting furnace: US Patent 20150139265[P]. 2015-05-21.
[8] WANG J, CHEN Y, ZHANG W, ZHANG C. Furnace structure analysis for copper flash continuous smelting based on numerical simulation[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(12): 3799-3807.
[9] 汪金良, 张传福, 张文海. 铅闪速熔炼过程的多相平衡模型[J]. 中南大学学报(自然科学版), 2012, 43(2): 26-31.WANG Jin-liang, ZHANG Chuan-fu, ZHANG Wen-hai.Multi-phase equilibrium model of lead flash smelting process[J].Journal of Central South University of Technology (Natural Science), 2012, 43(2): 26-31.
[10] 童长仁, 刘道斌, 杨凤丽, 吴金财. 基于元素势的多相平衡计算及在铜冶炼中的应用[J]. 过程工程学报, 2008(S1): 45-48.TONG Chang-ren, LIU Dao-bin, YANG Feng-li, WU Jin-cai.Multiphase equilibrium calculation based on element potential and its application in copper flash smelting[J]. The Chinese Journal of Process Engineering, 2008(S1): 45-48.
[11] 任鸿九. 有色金属熔池熔炼[M]. 北京: 冶金工业出版社,2001: 118-195.REN Hong-jiu. Nonferrous metal molten pool smelting[M].Beijing: Metallurgical Industry Press, 2001: 118-195.
[12] 汪金良, 张文海, 张传福. 硫化铅矿闪速熔炼过程的热力学分析[J]. 中国有色金属学报, 2011, 21(11): 2952-2957.WANG Jin-liang, ZHANG Wen-hai, ZHANG Chuan-fu.Thermodynamic analysis of lead sulfide flash smelting process[J]. The Chinese Journal of Nonferrous Metals, 2011,21(11): 2952-2957.
[13] LENNARTSSON A. Development of a process model for a Peirce-Smith converter[D]. Luleå: Luleå University of Technology, 2013: 17-24.
[14] TAN P, ZHANG C. Computer model of copper smelting process and distribution behaviors of accessory elements[J]. Journal of Central South University of Technology, 1997, 4(1): 36-41.
[15] FAN Y, ZHANG C, WU J, ZHAN J, YANG P. Composition and morphology of complicated copper oxalate powder[J].Transactions of Nonferrous Metals Society of China, 2010, 20(1):165-170.
[16] GAUTAM R, SEIDER W D. Computation of phase and chemical equilibrium: Part I. Local and constrained minima in Gibbs free energy[J]. AIChE Journal, 1979, 25(6): 991-999.
[17] NÉRON A, LANTAGNE G, MARCOS B. Computation of complex and constrained equilibria by minimization of the Gibbs free energy[J]. Chemical Engineering Science, 2012, 82:260-271.
[18] FREITAS A C D, GUIRARDELLO R. Comparison of several glycerol reforming methods for hydrogen and syngas production using Gibbs energy minimization[J]. International Journal of Hydrogen Energy, 2014, 39(31): 17969-17984.
[19] SHIMPO R, WATANABE Y, GOTO S, OGAWA O. An application of equilibrium calculations to the copper smelting operation[J]. Advances in Sulfide Smelting, 1983, 1: 295-316.
[20] NAGAMORI M, CHAUBAL P C. Thermodynamics of copper matte converting: Part Ⅲ. Steady-state volatilization of Au, Ag,Pb, Zn, Ni, Se, Te, Bi, Sb, and As from slag, matte, and metallic copper[J]. Journal of Electronic Materials, 1991, 20(12):319-329.
[21] SWINBOURNE D R, KHO T S. Computational thermodynamics modeling of minor element distributions during copper flash converting[J]. Metallurgical and Materials Transactions B, 2012,43(4): 823-829.
[22] SWINBOURNE D R, WEST R C, REED M E, SHEERAN A.Computational thermodynamic modelling of direct to blister copper smelting[J]. Mineral Processing and Extractive Metallurgy, 2011, 120(1): 1-9.
[23] 李明周, 童长仁, 黄金堤, 李俊标, 汪金良. 基于Metcal的铜闪速熔炼-转炉吹炼工艺全流程模拟计算[J]. 有色金属(冶炼部分), 2015, 67(9): 20-25.LI Ming-zhou, TONG Chang-ren, HUANG Jin-di, LI Jun-biao,WANG Jin-liang. Simulated calculation of overall process flow of copper flash smelting and converting based on Metcal[J].Nonferrous Metals (Extractive Metallurgy), 2015, 67(9): 20-25.
[24] ALCOCK C B, KUBASCHEWSKI O, SPENCER P J. Materials thermochemistry[M]. 6th ed. Oxford: Pergamon Press, 1993.
