基于共轭梯度法的低复杂度信道估计*
2015-03-25李臣阳高向川张卫党
李臣阳,高向川,张卫党
(郑州大学 信息工程学院,河南 郑州 450001)
基于共轭梯度法的低复杂度信道估计*
李臣阳,高向川,张卫党
(郑州大学 信息工程学院,河南 郑州 450001)
信道估计;大规模MIMO;共轭梯度法;导频污染
0 引 言
在大规模MIMO系统中,基站配置多根天线并与多个同信道用户同时通信已被引入下一代无线标准[1-2]。大规模MIMO(Massive MIMO) 时分双(Time Division Duplex, TDD)系统作为一种新颖的蜂窝网络结构成为当前的研究热点[3]。Massive MIMO通过增加基站天线的数量来扩大信道容量和提高信道估计性能,已经成为了一种关键技术[4-5]。利用信道互易性,信道训练的开销仅与每个小区的用户数相关,而与基站天线数无关,因此,当基站天线数趋向无穷时,并不会增加系统的反馈开销而且文献[6]已证明额外多出来的天线总是对性能有益的。
共轭梯度法最早是由Hestenes和Stiefle于1952年提出来的,用于解正定系数矩阵的线性方程组[7-8],在这个基础上,Fletcher和Reeves(1964)首先提出了解非线性最优化问题的共轭梯度法[9]。共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。由于共轭梯度法不需要矩阵存储,且有较快的收敛速度和二次终止性等优点,现在共轭梯度法已经广泛地应用与实际问题中。在本文中,我们将求逆过程转化为解方程组的问题,然后通过共轭梯度法近似求解去降低其复杂度。
1 信道模型
我们假设基站端配置Nr根接受天线,发射端配置Nt根接受天线,为了估计准静态平坦衰落信道H∈Nr×Nt的瞬时MIMO信道系数,信道矩阵H建模为,其中非零均值矩阵H意味着可能存在视距传播,并且协方差矩阵R∈NtNr×NtNr是半正定。考虑到R一般不是一个经过缩放的单位矩阵,但描述了空间传播环境,我们使用与文献[10-12]一样的导频信号,也就是发射机发射一个预定的导频P∈Nt×B,接收机接收到的信号Y∈Nr×B由下公式得到:
Y=PH+N
(1)
式中,N∈Nr×B循环对称复高斯干扰,干扰协方差矩阵S∈NrB×NrB是正定的,它包括常规的非相关接收机噪声和不同类型的来自其他系统的干扰,在大量的大规模MIMO参考文献中[4,13-16],后者通常称为导频污染。矩阵R和S被假设在发射器和接收器已知。
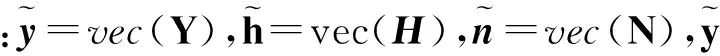
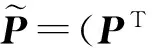
(2)
式中,I为一个Nr×Nr的单位阵,则由以上几个式子可已将信道模型表示为:
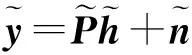
(3)
如果接收端已知信道和噪声的统计信息,那么BayesianMMSE估计结果为[10-12,17]:
(4)
然后得到估计误差:
(5)
最近,对大规模MIMO系统的研究兴趣日益增加,在基站接收端可能会装置有数百个天线,为了估计每根天线的信道信息,导频序列长度B要和发射天线数Nt相同[3-4]。在大规模MIMO系统在TDD模式下,在利用信道互易进行信道估计时总有Nt 假设在一个大规模MIMO系统中,Nt=20,Nr=200,那么MMSE估计就需要对一个4 000×4 000的矩阵进行求逆。由于R和S随时间的变化,这种大规模的操作需要相当频繁。本文的目的是要用一种迭代方法对求逆的过程进行优化,使计算复杂度和估计性能之间达到一种平衡。 (6) 共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜素,求出目标函数的极小点。 对于二次函数: f(x)=1/2xHAx+bHx+c (7) 式中,x为n维矩阵,A是对称正定矩阵,c为常数。首先我们给定一个任意初始点x(1),计算出目标函数f(x)在该点的梯度g(1),若‖g(1)‖<ε,ε为无穷小量,则停止计算,否则令: d(1)=-f(x(1))=-g(1) (8) 式中,d(1)搜索方向称为最速下降方向,沿方向d(1)搜索,得到点x(2),然后计算在x(2)处的梯度,若‖g(1)‖>ε,则利用-g(2)和d(1)构造第2个搜索方向d(2),再沿d(2)搜索。一般地,若已知点x(k)和搜索方向d(k),则从x(k)出发,沿d(k)进行搜索,得到: x(k+1)=x(k)+λ(k)d(k) (9) 式中,迭代步长λ(k)满足: (10) 此时可求出λ(k)的显示表达式: (11) 利用-g(k+1)和d(k)构造下一个搜索方向d(k+1),并使d(k)和d(k+1)关于A共轭。令: d(k+1)=-g(k+1)+β(k)d(k) (12) 上式两端左乘d(k)HA可解得: (13) 再从x(k+1)出发,沿方向d(k+1)进行搜索。 共轭梯度法具体过程如下算法: 1.给定任意初始点x(1)和精度要求ε。 (14) 为评估提出的估计算法的性能,设定在大规模MIMO系统中,Nr=100,Nt=10,导频长度B=10。不失一般性,设定零均值的信道和干扰。我们遵循克罗内克模型[18]来描述目标信道和干扰信道天线之间的相关性。在仿真中,MIMO系统的协方差矩阵被模拟为:R=Rt⊗Rr,其中Rt∈Nt×Nt和Rr∈Nr×Nr分别为发射端和接收端的协方差矩阵。干扰小区和目标小区模型一样,第i个干扰小区的协方差矩阵为Rti⊗Rri,β≥0,U为干扰小区集合,β因子表示该污染小区的污染严重程度。β=0时表示噪声受限情况,β=1表示干扰受限情况。 我们利用归一化的MSE作为我们度量性能的标准: (15) 在图1中,画出了β=0、0.1、1,迭代次数N=40情况下,估计误差MSE和信噪比SNR的关系。在图1中可以看出,在β=0 噪声受限情况下,MMSE估计器随着信噪比的增加,估计精度趋于0,在β≠0时,由于存在导频污染,估计精度趋于一个非零值;我们还可以看出在信噪比较低时,基于共轭梯度法的信道估计精度并没有降低,只有在信噪比较高时,由于逼近误差所产生的偏差,MSE会有所下降。在存在导频污染的情况下,对于任意固定的迭代次数N,随着信噪比的增加,基于共轭梯度法的信道估计和传统的MMSE信道估计一样,MSE最终均收敛到一个非零值。而且干扰情况越严重,基于共轭梯度法的估计性能越接近于MMSE估计器,当β=1时,基于共轭梯度法的估计性能与MMSE估计器是完全相同的。 图1 不同干扰情况下MSE随着SNR 的变化 在图2中,信噪比SNR设定为5 dB,迭代精度ε=0.001,我们可以看出,随着迭代次数的增加,基于共轭梯度法的信道估计误差一直在降低。而且β=0、0.1、1时,迭代次数N=45、45、30,本文所提出的优化算法就能够达到MMSE估计器的估计性能。也就是说迭代次数很小就能够达到传统MMSE估计的性能,而且45≪1 000,在复杂度方面降了一个数量级。 图2 不同干扰情况下MSE随着迭代次数N的变化 通过使用信道的二阶统计信息,Bayesian MMSE信道估计获得了良好的性能。但是在大规模MIMO系统中,天线尺寸非常大,由于再利用Bayesian MMSE方法进行信道估计时,存在协方差矩阵的逆,所以这将是一个极其复杂的过程。在本文中,我们将求逆的过程转化为解方程组的问题,然后利用共轭梯度法通过迭代取得方程组的近似解,以此来降低Bayesian MMSE估计方法的复杂度。而且随着迭代次数的增加,基于共轭梯度法的信道估计性能无线接近于Bayesian MMSE的信道估计性能。并且,在迭代次数很小的时候,就可以达到Bayesian MMSE的估计精度。 [1] Paulraj A J, Gore I A, Nabaret R U, et al.An Overview of MIMO Communications-A Key to Gigabit Wireless.Proc. of the IEEE, 2004, 92(2):198-218. [2] 高向川,刘晓叶,高小梅. 三小区多用户MIMO系统中干扰对齐优化算法[J]. 通信技术,2014,47(09):989-993. GAO Xiang-chuan, LIU Xiao-ye, GAO Xiao-mei. Improved Interference Alignment Alogorithm for Three-Cell Multi-User MIMO System[J]. Communications Technology, 2014, 47(09):989-993. [3] Jose J, Ashikhmin A, Marzetta T, and Vishwanath S. Pilot Contamination and Precoding in Multi-Cell TDD Systems. IEEE Trans. Commun., vol. 10, no. 8, pp. 2640-2651, 2011. [4] Hoydis J, Brink S, ten, and Debbah M. Massive MIMO in the UL/DL of Cellular Networks: How Many Antennas Do We Need?. IEEE J. Sel. Areas Commun., vol. 31, no. 2, PP. 160-171, 2013. [5] Rusek F, Persson D,Lau B, Larsson E, Marzetta T, Edfors O, and Tufvesson F. Scaling up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag., vol. 30, no. 1, pp. 40-60, 2013. [6] Dahrouj H, YU W. Coordinated Beamforming for the Multicell Multi-Antenna Wireless System. IEEE Trans. Wireless Commun., 2010, 9(5):1748-1759. [7] Hestenes, Magnus R. and Stiefel, Eduard (December, 1952). Methods of Conjugate Gradients for Solving Linear Systems. Journal of Research of the National Bureau of Standards 49 (6). [8] Saad Y. Chapter 6: Krylov Subspace Methods, Part I. Iterative methods for Sparse Linear systems. 2nd. SIAM. 2003. ISBN 978-0898715347. [9] Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-based Algorithms.Springer Publishing. ISBN 0-387-24348-8. [10] J Kotecha and A Sayeed. Transmit Signal Design for Optimal Estimation of Correlated MIMO Channels. IEEE Trans. Signal Process.,vol. 52,no. 2,pp.546-557,2004. [11] LIU Y, WONG T, and Hager W. Training Signal Design for Estimation of Correlated MIMO Channels with Colored Interference. IEEE Trans. Signal Process., vol. 55, no. 4, pp. 1486-1497, 2007. [12] E Bjo rnson and B Ottersten. A Framework for Training-based Estimation in Arbitrarily Correlated Rician MIMO Channels with Rician Disturbance.IEEE Trans. Signal Process., vol. 58, no. 3, pp. 1807-1820, 2010. [13] Marzetta T. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas. IEEE Trans. Wireless Commun., vol. 9, no. 11, pp. 3590-3600, 2010. [14] Jose J,Ashikhmin A, Marzetta T, and Vishwanath S. Pilot Contamination and Precoding in Multi-Cell TDD Systems. IEEE Trans. Commun., vol. 10, no. 8, pp. 2640-2651, 2011. [15] Rusek F, Persson D, Lau B, Larsson E, Marzetta T, Edfors O, and Tufvesson F. Scaling up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag., vol. 30, no. 1, pp. 40-60, 2013. [16] Larsson E, Tufvesson F,Edfors O, and Marzetta T. Massive MIMO for Next Generation Wireless Systems. IEEE Commun. Mag., to appear. [Online]. [17] Kay S. Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall, 1993. [18] D S Shiu, G Foschini, M Gans, and J Kahn. Fading Correlation and Its Effect on the Capacity of Multielement Antenna Systems. IEEE Trans. Commun., vol. 48, no. 3, pp. 502-513, 2000. Low-ComplexityChannelEstimationbasedonConjugateGradient LIChen-yang,GAOXiang-chuan,ZHANGWei-dang (InformationandEngineeringCollege,ZhengzhouUniversity,ZhengzhouHenan450001,China) In consideration of pilot-based channel estimation in large-scale MIMO (Multiple-Input Multiple-Output) communication systems,hundreds of antennas are equipped at the base station. Conventional MMSE estimator enjoys good performance in the estimation accuracy, and however, when MMSE channel estimation method is used to implement estimation,the operation of covariance matrix inversion would result in computational complexity ofO(M3),Mmeaning the dimension of channel covariance matrix,and when the base station is equipped with hundreds of antennas, this would be an extremely complex process. To solve this problem, the inversion process is transformed into solution of linear equations, thus the computation complexity of the whole process is reduced toO(NM2) through conjugate gradient method,Nmeaning the iterations number of conjugate gradient algorithm andN≪M. channel estimation; large-scale MIMO; conjugate gradient; pilot contamination 10.3969/j.issn.1002-0802.2015.11.002 2015-06-15; 2015-09-20 Received date:2015-06-15;Revised date:2015-09-20 国家自然科学基金(No.U1204607) Foundation Item:National Natural Science Foundation of China(No.U1204607) TN A 1002-0802(2015)11-1213-04 李臣阳(1991—),男,硕士研究生,主要研究方向为无线移动通信,大规模MIMO; 高向川(1981—),男,副教授,博士,主要研究方向为无线移动通信,大规模MIMO,干扰对齐,第五代移动通信关键技术研究; 张卫党(1958—),男,教授,博士,主要研究方向为通信技术研究 。2 共轭梯度法



3 仿真分析
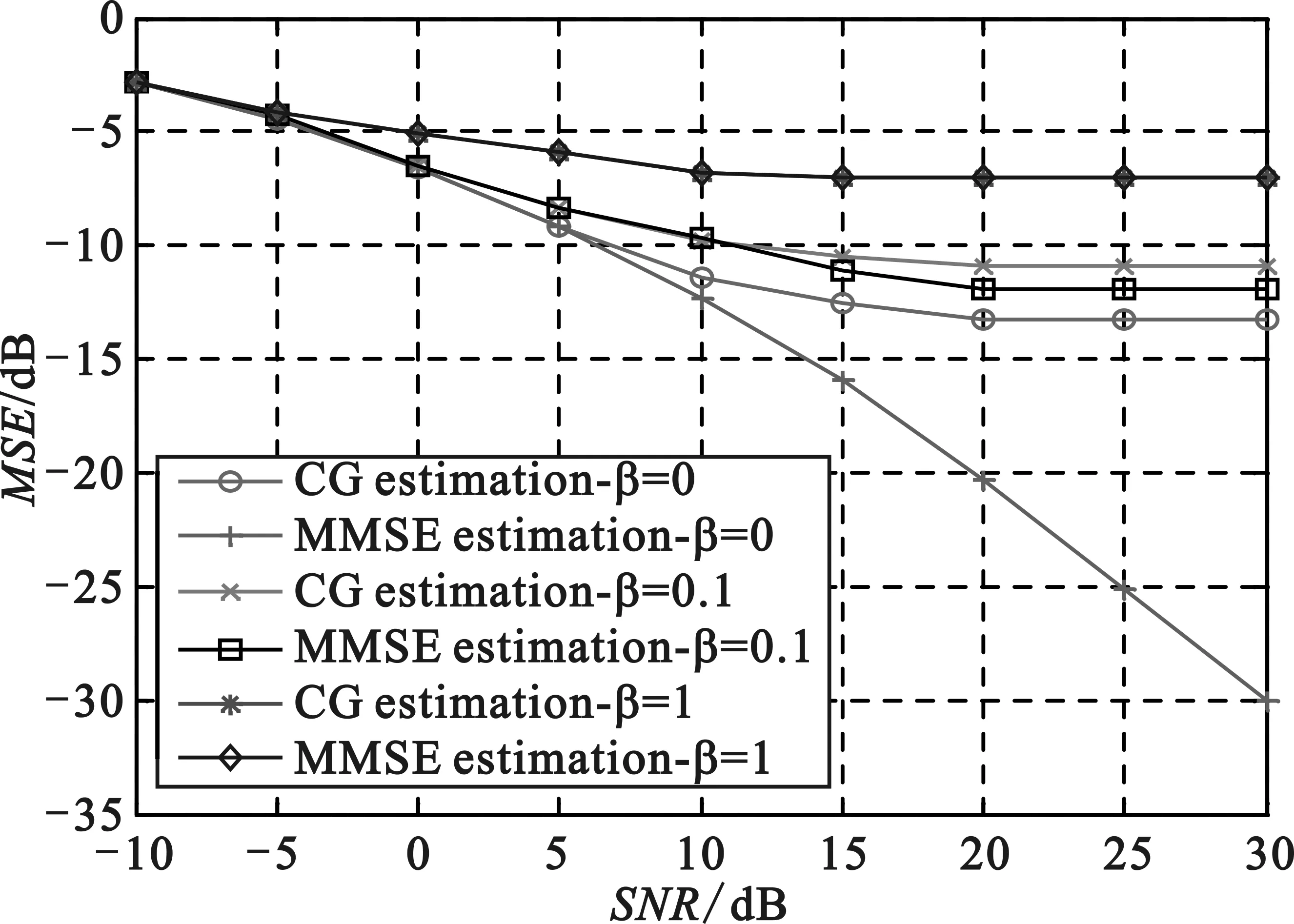

4 结 语

