小水线面双体船阻力及航态预报方法

龚家烨，李云波，常赫斌

(1.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001;2.中国船舶及海洋工程设计研究院，上海200011)

小水线面双体船(small waterplane area twin hull，SWATH)波浪中良好的试航性能使其在军用和民用上均具有良好的应用前景。小水线面船型的不足是湿表面积大导致阻力大，航行姿态受排水量影响敏感，小的排水量变化会引起较大的吃水和姿态变化，航行中容易出现埋首现象。这些涉及到船舶安全航行的问题也是船型研发和设计中要解决的关键技术问题。

解决上述问题需要能够准确预报小水线面双体船的阻力、航行姿态、姿态变化对阻力的影响、船体周围的流线分布情况，进而指导船型优化、鳍等附体布置及运动姿态改善等。而目前对于小水线面双体船型阻力的预报方法多为粘流理论、薄船理论以及一些商用软件。粘流方法难以达到快速预报的目的，薄船理论则难以对船体周围兴波以及航行姿态进行模拟，而Rapid等商用软件常常需要通过升高面元特殊处理来实现自由表面的收敛。因此，探讨有效的理论方法来支撑上述研究与预报在目前小水线面船型研发设计中是迫切需要的。

本文在现有小水线面双体船阻力预报研究的基础上［1－4］，基于Dawson方法［5］，针对上述船舶阻力、运动姿态和流线分布预报问题，探讨理论预报方法与数值计算方法［6－12］。采用变化的边界网格，在船舶运动姿态变化过程中实时进行湿表面积划分及迭代，给出计及航行姿态和兴波变化影响的船舶阻力预报方法;通过不断迭代给出航行的升沉和纵倾值。通过船体周围流线模拟和迭代完善，预报船体近远场兴波、兴波阻力及总阻力。

研究表明，本方法可进行快速的船舶周围流场、兴波、运动姿态和阻力预报，可从兴波及干扰、流场分布、船舶阻力和运动姿态等角度进行船体水动力作用原理分析，支撑进行船型优化、附体布置，进而研发设计出具有较好水动力性能的船型具有重要的理论和实际意义。

1 数学模型及数值方法

1.1 基本模型

采用随船坐标系，如图1所示。坐标系原点o位于船舶中心，z轴垂直向上，x轴由船艏指向船艉，y轴指向右舷为正，xy平面与静水面重合。

图1 坐标系Fig.1 Coordinate system

假设流体理想，流动定常，无限水深，船舶兴波为微幅波。流场速度势ψ分解为无自由面影响的重叠模速度势φ和考虑自由液面作用的扰动速度势φ，即

基于上述假设，可知φ≪φ。

流场中有

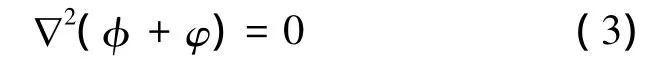
物面上满足:

式中:n=nxi+nyj+nzk为物面法向量.

自由面z=ζ(x，y)上满足:

速度势满足远处趋于零的远方辐射条件。

1.2 流线速度势自由面边界条件

考虑到φ关于静水面对称，则

在z=ξ和z=0上对速度势展开，忽略φ的非线性项，可得z=0上简化的自由面边界条件:

假设▽φ▽φ=φlφl，可得重叠模流线速度势表示的自由面条件:

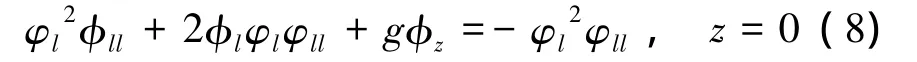
式中:l为重叠模流线方向。

1.3 奇点分布及数值计算模型

将船体和自由表面进行数值离散，取船体网格数为Nb，自由面网格数Nf，以四边形网格为主，船体首尾局部采用三角形网格进行特殊处理，自由面采用贴水线网格，半自由面网格示意图如图2。

图2 小水线面双体船自由面网格Fig.2 Typical mesh for free surface of one SWATH

离散单元布置源汇后，控制点p处重叠模流场速度势表示为

式中:SB表示物面，σB0为物面控制点处源强，rpq为任意源点q到控制点p的距离。

对式(9)离散，并代入物面不可穿透条件可得p趋近于物面时:

扰动速度势φ也可用相同方法进行数值离散。

采用改进后的差分方式求解方程(8)，将流线差分坐标变换为关于横纵向网格的差分，沿纵向网格采用四点向前差分方式，横向网格则采用中心差分来计算，因此自由面条件中流线速度势的二阶偏导数φll、φll的计算，以φll为例表示为

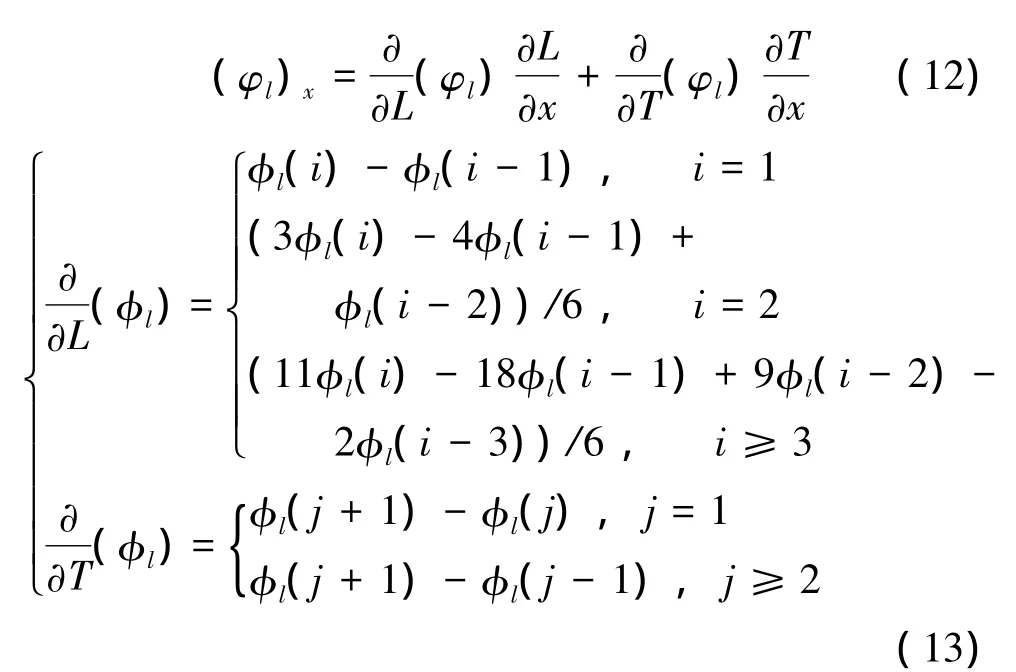
纵向差分中，当i=1时，其上游网格i=0为虚单元，仍然计算其受到的单位诱导速度，但其源强为零。横向差分中，与船体水线相邻的网格j=1取与其相邻网格j=2计算两点差分，与边界相邻的网格仍然采用虚单元的方法计算中心差分。

式(12)中(∂L/∂x)、(∂T/∂x)通过坐标转换得

式中:J为雅各比矩阵。代入求解物面方程(4)和自由面条件(8)可得物面源强σB0、σB1和自由面源强σF。

1.4 兴波阻力及深沉、纵倾的计算

船体表面控制点压力系数Cpi和船体受到的兴波阻力Rw、兴波阻力系数Cw、升力Fz和纵倾力矩Ny表示为

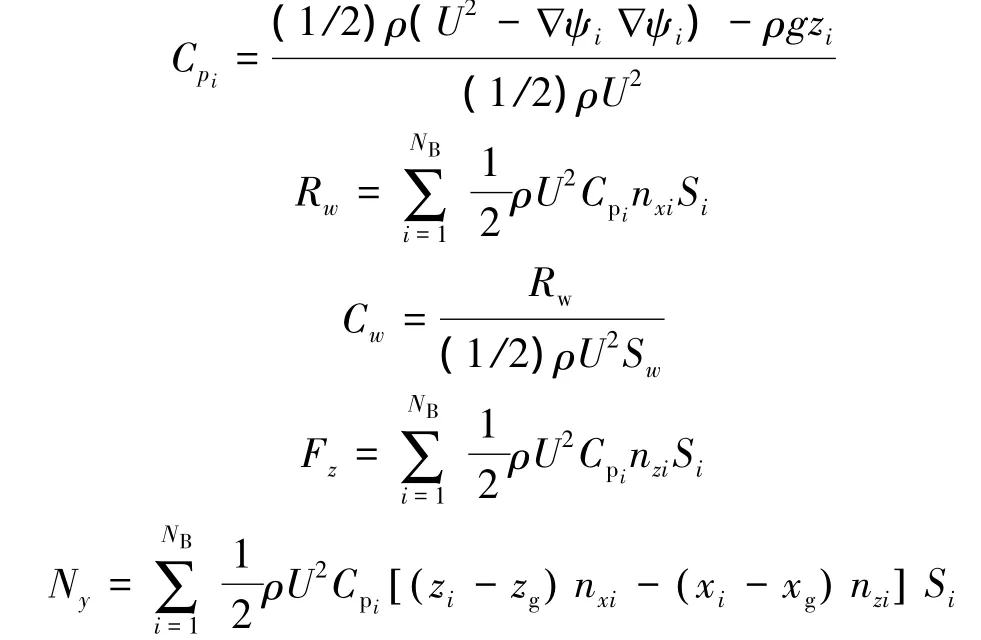
式中:Sw表示船体的湿表面积，xi、zi为控制点坐标，xg、zg为船舶的重心坐标，nxi、nzi为单元法线方向。

给定时间步长Δt，可以得到船舶下一时刻的吃水St+Δt以及纵倾值Tt+Δt:

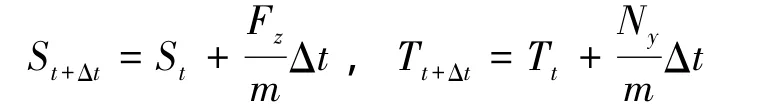
对船体水线以下近水面处局部网格进行实时划分，而不发生出水或入水的大部分网格始终保持不变。由于小水线面双体船型支柱相对规整的船型特点，使得其包括潜体在内的绝大多数网格保持不变，仅仅需要对支柱接近水线部分网格进行重新插值与划分，这样既减小了网格重新离散带来的误差，也节省了计算时间。通过反复迭代直到满足收敛条件(Fz＜ε、Ny＜ε)即可得到考虑船体姿态变化影响的兴波阻力，进行船体姿态预报。

2 数值计算方法研究

2.1 波面网格划分及探讨

为了在较大弗汝德数范围内能够获得较准确的兴波波形，本研究对网格划分及形式进行了研讨。自由面网格沿纵向从船艏向远前方、船艉向后方呈辐射状，网格长度按比例rx递增，参考尺度为波长:

式中:Lwl为水线长。

单个波长网格数随弗汝德数增加而减少，但至少保证一个波长30个网格，以免造成内存的浪费或计算精度的不足。横向网格尺度按ry向外递增。

2.2 自由表面处理及模拟

为了准确模拟兴波，在自由面单元间切向诱导速度处理时，考虑到面源正负面切向速度连续性，将控制点上移一定高度以消除奇点影响获得较好计算结果。上移距离与纵向网格尺寸成一定比例联动变化。研究中发现，控制点位于单元中心时，单元对本身切向诱导速度贡献约为零，这在数值差分时易造成自由面波形的震荡及不稳定，本研究进行了控制点前移处理，进行了不同前移比例对计算结果及色散影响研究。最后建议自由面所有控制点前移0.1个单元长度可以得到较好的数值模拟结果。

2.3 压力积分影响及出水点的求解

研究发现，由于压力积分时控制点压力小于零的网格为出水网格，忽略其对阻力及航态的影响。因此，按照传统的网格划分方式垂向网格过少，很难较为精确地区分开船体出水部分，尤其对升力和船体深沉的计算结果有较大的影响。但是垂向网格过多又增大所需内存和计算速度。因此本文探讨了求得控制点压强后，对垂直方向的每一列网格进行细化，对细化前所求得的各控制点压强进行垂向线性回归，插值得到细化后网格控制点的压强及特殊点。通过上述处理可以提高船体运动姿态及不同航态下的湿表面积预报精度。

3 算例及结果分析

3.1 排水式船体数值计算及验证

采用Wigley船型，对不同的数值处理进行探讨，从而得出较优的参数设置。Wigley船型其数学表达式为

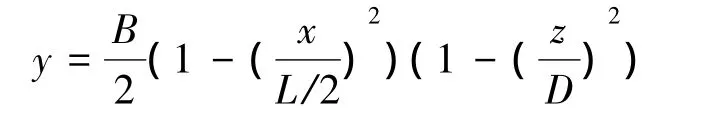
式中:L为船长，B为船宽，D为吃水，B=L/10，D= L/16。

沿船体基础网格数1 584个，自由面2 968个(Fr=0.316)。网格大小随弗汝德数变化进行联动调整，网格划分如图3、4。

图3 Wigley船体网格划分Fig.3 Mesh for Wigley hull

图4 自由面网格(Fr=0.316)Fig.4 Mesh for free surface of one Wigley(Fr=0.316)

探讨了控制点升高高度对数值计算结果影响。取Dx为单元长度，共讨论了4个方案。方案1～4分别为控制点升高 Dx/20、Dx/40、Dx/80及定值0.000 1的计算。

将方案1～3结果与试验和Rapid商业软件参考值进行对比，对比结果和波形模拟见图5、6。

图5 兴波阻力系数(方案1～3)Fig.5 Coefficients of wave making ressitance(case 1-case 3)

图6 方案3波形图(Fr=0.316)Fig.6 Wave pattern of case 3(Fr=0.316)

图5可以看出，弗汝德数低于0.35时，不同方案计算结果差别不大且与剩余阻力系数试验值相符良好。但随着弗汝德数增大，方案1、2的数值计算结果与试验结果偏差逐渐增大。升高比例为Dx/80的方案3与试验结果相符良好，且表现出较好的非线性效果。由上述可见，控制点升高比例不宜过大，选取Dx/80可以获得较好的数值。从图6也可以看出，方案3可以较好的模拟船体兴波波形，且不会引起自由面的震荡。

再将方案1～3中的最优方案3、4及试验和Rapid商业软件参考值对比，如图7～10。

图7 兴波阻力系数(方案3、方案4)Fig.7 Coefficients of wave making ressitance(case 3，case 4)

图8 升沉曲线(方案3、方案4)Fig.8 Curves of sinkage(case 3、case 4)

图9 纵倾曲线(方案3、方案4)Fig.9 Curves of trim(case 3，case 4)

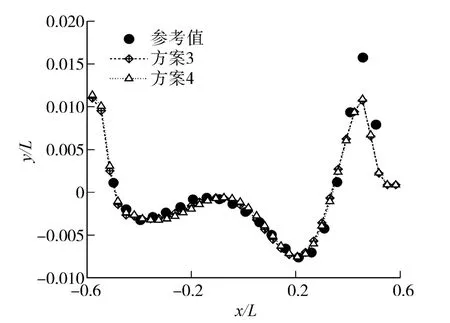
图10 船侧面波形图(方案3、方案4)(Fr=0.316)Fig.10 Wave profile along ship(case 3、case 4)(Fr=0.316)

图7～10可见，控制点上移随网格调整可提高计算精度，尤其对兴波阻力和纵倾预报尤为明显。由方案3结果与商业软件非线性计算参考值进行比较也可以看出，采用本研究探讨的数值计算方法，对非线性问题在较大弗汝德数范围内具有较好的预报精度。

由图7可见，弗汝德数小于0.4范围内，本文方法无论数值计算结果还是曲线变化趋势均与试验结果有较好的相符度。由图10可见，本研究模拟的兴波波高与试验值结果相符良好，仅船艏相对试验结果较低，主要原因可能是忽略了粘性影响及贴船体处的网格划分处理所致.

3.2 小水线面双体船数值计算及结果分析

采用本研究方法对多型小水线面船型在弗汝德数0.1～0.45较大的范围内进行了对比分析和验证。由于数值偏差和曲线变化趋势是类似的，因此以某一型为例进行说明。船体和自由面网格数分别为1 500个和2 800个，船体网格示意图见图11。

图11 某小水线面双体船网格划分Fig.11 Mesh for one SWATH

利用该理论方法预报了该船兴波阻力、升沉和纵倾，采用粘流理论预报了粘性阻力，进而得到总阻力。将本方法所得数值预报结果与不考虑航态影响的约束模数值结果和试验值进行比较，见图12～15。

图12可见，计及航态的兴波阻力系数计算结果与试验所得剩余阻力曲线的趋势是完全吻合的，峰谷值也相互对应。图13的总阻力系数对比可以看出，约束模的总阻力系数计算结果与试验值具有较大偏差。考虑航态影响的总阻力系数曲线与在弗汝德数0.35之前几乎穿过试验点，且在峰值点的大小及相位上均与试验结果相符良好。由于弗汝德数0.35相当于水线长 100 m的小水线面双体船约20 kn航速，可满足多数该船型阻力预报和设计需求。弗汝德数0.35后理论预报结果略小于试验值，最大偏差在15%。主要原因是高速高阶效应和粘性效果影响理论预报结果。

图12 计算兴波阻力系数与试验数据比较Fig.12 Comparison of computed wave making resistance coefficient with experimental data

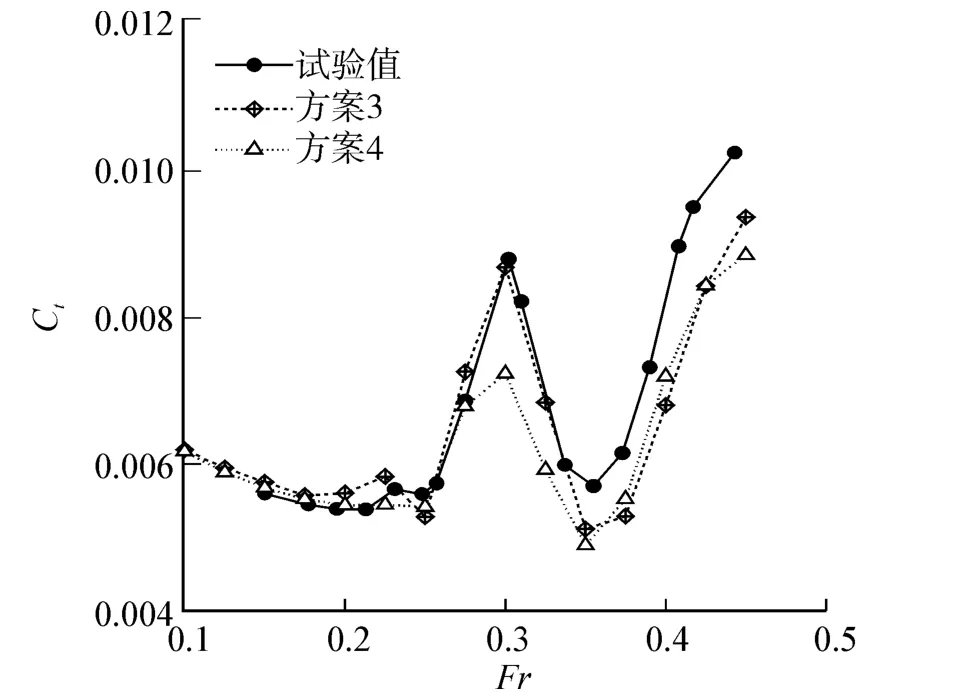
图13 计算总阻力系数与试验数据比较Fig.13 Comparison of computed total resistance coefficient with experimental data

图14 计算纵倾值与试验数据比较Fig.14 Comparison of computed trim with experimental data

从图14、15可以看出，数值模拟的升沉、纵倾值与试验值的变化趋势相符。纵倾值在弗汝德数0.3左右有偏差，升沉预报与试验结果符合较好。

该船型在Fr=0.3时产生的兴波如图16、17所示，可以看出兴波也很好地满足了远方辐射条件。

图15 计算升沉值与试验数据比较Fig.15 Comparison of computed Sinkage with experimental data

图16 波形图(Fr=0.3)Fig.16 Wave pattern(Fr=0.3)

图17 波形云图(Fr=0.3)Fig.17 Cloud picture of wave pattern(Fr=0.3)

4 结论

1)通过数值计算方法改善，可以在非全非线性自由面条件下改善数值预报结果，获得小水线面双体船阻力及航行姿态较好的预报结果。

2)采用本论文的理论预报方法，可以克服很多方法在自由面模拟的发散和震荡问题，可以快速实现数值迭代收敛过程，计算结果稳定。

3)利用本文的方法，对小水线面船舶可以较好的预报船舶航行姿态以及湿表面积变化，尤其对小水线面船型优化和附体设计具有很好的指导作用。

4)由于采用无升力源汇模型，因此对于双体之间的兴波干扰难以准确模拟，在今后的工作中需要对预报所采用的模型改善。

［1］邹早建，罗青山，史一鸣.小水线面双体船阻力预报研究［J］.中国造船，2005，46(1):14－21.

ZOU Zaojian，LUO Qingshan，SHI Yiming.A research on resistance prediction of SWATH ships［J］.Shipbuilding of China，2005，46(1):14－21.

［2］羊少刚，李干洛，余灵.高速双体船兴波阻力的数值计算［J］.华南理工大学学报:自然科学版，1995，23(10):16－25.

YANG Shaogang，LI Ganluo，YU Ling.Numerical calculation of wavemaking resistance of high－speed catamaran［J］.Journal of South China University of Technology:Natural Science，1995，23(10):16－25.

［3］黄鼎良.小水线面双体船性能原理［M］.北京:国防工业出版社，1993.

［4］陈京普，朱德祥，何术龙.双体船/三体船兴波阻力数值预报方法研究［J］.船舶力学，2006，10(2):23－29.

CHEN Jingpu，ZHU Dexiang，HE Shulong.Research on numerical prediction method for wavemaking resistance of catamaran/trimaran［J］.Journal of Ship Mechanics，2006，10 (2):23－29.

［5］DAWSON C W.A practical computer method for solving shipwave problems［C］//Proceedings of the Second International Conference on Numerical Ship Hydrodynamics.Beckly，1977: 30－38.

［6］RAVEN H C.Variations on a theme by Dawson［C］//17th Symposium on Naval Hydrodynamics.The Hague Netherlands，1988:151－171.

［7］TARAFDER M S，SUZUKI K.Numerical calculation of freesurface potential flow around a ship using the modified Rankine source panel method［J］.Ocean Engineering，2008，35 (5/6):536－544.

［8］RAVEN H C.A solution method for the nonlinear ship wave resistance problem［D］.Delft:Delft University of Technology，1996.

［9］FLODÉN D，KIM K，OTTOSSON P.A computational/experimental investigation on resistance and seakeeping characteristics of trimaran configuration in comparison with monohull［C］//The 9th Symposium on Practical Design of Ships and Other Floating Structures.Luebeck－Travemuende，Germany，2004.

［10］荻原誠功.Rankine sourceによる船体まわりの流れの近似計算法［J］.関西造船協会誌，1983:190.

［11］刘应中.船舶兴波阻力理论［M］.北京:国防工业出版社，2003:81－91.

LIU Yingzhong.Theory of ship wave making resistance［M］.Beijing:National Defense Industry Press，2003:81－91.

［12］王中，卢晓平，王玮.考虑升沉和纵倾的方尾船非线性兴波阻力计算［J］.水动力学研究与进展，2010，25(3): 422－428.

WANG Zhong，LU Xiaoping，WANG Wei.Nonlinear wave making resistance calculation for transom－stern ship with consideration of sinkage and trim［J］.Chinese Journal of Hydrodynamics，2010，25(3):422－428.