网络情感传播下的社会救灾物资选址问题研究

李 清， 胡志华

(1.同济大学 经济与管理学院， 上海 200092； 2.上海海事大学 物流研究中心， 上海 201306)



李 清1,2*， 胡志华2

(1.同济大学 经济与管理学院， 上海 200092； 2.上海海事大学 物流研究中心， 上海 201306)

社会救援在应急救援中发挥着重要作用.网络加快了信息和情感的传播，让更多人加入物资捐赠活动.社区是物资收集的最小单位，其收集的物资由临时集中点统一管理并送至汇总点.本文以最小化经济成本、最大化募集物资量为目标建立模型，选择临时收集点.以上海市浦东新区的37个街道办事处为单位，考虑情感传播下物资的收集模型，设计实验进行参数敏感性分析，并对两个目标进行Pareto分析.

网络情感； 社会物资； 选址

工业进步导致环境日益恶化，突发灾害频繁发生.灾害不仅给人类的生命和财产带来很大影响，也对社会造成了巨大冲击.救援资源由政府和社会提供，应急救援资源需求波动性大、需求时限短的特点决定了社会救援在应急救援中发挥着重要作用.救援物资的分配问题得到了广泛研究：在应急分配调度方面，徐苒[1]建立了应急物资中转站选址的机会约束模型，采用遗传算法寻求最优方案.杨勃[2]提出启发式算法求解多受灾点、多救灾物资的分配调度问题.针对多出救点问题，刘春林[3]提出以最早应急开始时间为目标的数学模型及求解算法；给出了应急时间最早前提下出救点数目最少和限制期条件下出救点数目最少的应急模型[4].网络等的兴起改变了信息、情感的传播方式和速度：F. Chierichetti[5]研究了偏好依附模型中舆情传播的效果；基于网络舆情传播理论，李纲[6]提出了Web2.0环境下企业网络舆情的“过程模型”；R. Johnson[7]调查了邮件网络中信息、数据对人们关系和社交网络的影响.兰月新[8]构建数学模型分析突发事件网络谣言的传播机理，寻找控制谣言传播的对策；潘芳[9]建立危机事件中网络舆情传播模型，提出应对不同消极思潮的对策.

城镇化建设下居民集中度高，社区成为人们捐赠物资的最小单位.本文建立双目标0-1整数规划模型，以最小化经济成本、最大化救援物资量为目标，确定物资的临时收集点.社区为物资收集单位，收集点合并物资并在截止时间前运送到汇总点.物资收集过程中网络的运用能加快信息和情感的传播，增加物资收集量.

1 问题描述与定义

1.1 问题描述

计算机和网络的普及加快了消息的传播速度.接触到灾情信息的群众及时参与救援，也带动更多的人加入捐赠.物资募集方式如图1：从一定区域内的社区中选择临时收集点收集物资，合并后送往汇总点，汇总点检验后运往灾区.由于人员、场地等限制，同一时间只能接待一个临时收集点的物资.考虑到救灾的紧迫性，各社区的物资收集时间有严格限制，目标是在限定的时间内收集到尽可能多的物资.

图1 募集物资的供应链结构
Fig.1 The supply chain structure of material collection

1.2 网络情感传播

互联网成为现代社会表达和传播不同情绪、态度和意见的有效平台，信息传播的乘数效应会掀起较强烈的社会反映.相对于传统媒介，微博、微信、QQ等网络工具的流行使信息以“裂变”方式传播，对已有舆情传播模型提出挑战.陈波[10]借鉴传染病模型，建立带直接免疫的SEIR舆情传播控制模型；V. Isham[11]研究网络中病毒和谣言的随机传播，运用蒙特卡洛模拟方法；潘新[12]考虑个体间的相互作用，提出基于社会网络分析的舆情传播模型.为揭示微博复杂网络中的舆情传播演化机理，朱恒民[13]以有向无标度网络为载体建立舆情传播SIRS模型.M. Nekovee[14]介绍病毒谣言传播的随机模型，推导平均场方程描述复杂社会网络的动态模型.本文根据网络情感传播建立物资收集模型.

1.3 选址问题求解方法

S. L. Hakimi等[15-16]、C. Toregas等[17]、J. R. Weaver等[18]考虑了3类基本的应急选址问题.C. G. Rawls等[19]建立双层随机混合整数模型研究应急资源分配点预选址.詹沙磊等[20]建立多目标随机规划模型研究多出救点、多受灾点和多应急物资的出救点选址问题.张敏等[21]基于应急设施失效问题，建立最大覆盖选址模型.P. Murali等[22]考虑运输距离与不确定需求，研究医疗设施最大覆盖选址问题.骆正清等[23]综合考虑随机应急需求和应急配送时间，建立模糊和随机混合机会约束规划选址模型.在不确定应急需求和物流网络下，陶莎等[24]研究应急配送中心选址问题，采用期望值法和随机模拟法处理数学模型中的不确定性.S. Rath等[25]利用数学启发式算法研究灾害救援中中间仓库的选址问题.Y.H. Lin等[26]运用两阶段启发式算法确定临时仓库的位置及其对需求点的分配.Z.H. Hu等[27]在考虑最小化心理成本的同时研究灾后废墟的逆向物流管理.基于上述文献，本文研究社会应急资源募集地选址问题.

2 模型

2.1 符号定义

3)决策变量.xi，k：若社区i的物资由k集中，xi，k=1；yk：若k被选为物资集中点，yk=1.

2.2 模型

[M1] MinimizefC=fM+fD+fT+fS,

(1)

(2)

(3)

(4)

(5)

(6)

s.t.

(7)

yk≥xi，k，∀i，k,

(8)

(9)

(10)

(11)

(1)和(2)式为目标函数，(1)式表示最小化物资收集成本，(2)式表示最大化物资收集量.货币成本主要包括：收集成本、运输成本、转运成本以及建设成本，分别对应式(3)～(6).

(7)～(11)为约束条件，(7)表示任一社区的物资只能送到一个临时收集点.(8)表示社区物资只能送往建立临时收集点的社区.(9)表示临时收集点汇总的物资量必须在其容量范围内.(10)表示社区剩余的物资收集时间与社区间运输时间之和不能超过允许的总时间.(11)限定了临时收集点的最小容量.

首先分别求出单个目标下问题的最优解.

(12)

s.t. (9)～(11),

[M2b]MinimizefC=fM+fD+fT+fS,

(13)

s.t. (3)～(8).

接着对目标函数进行标准化处理，将多目标转换为单目标：

[M3] Minimize

(14)

s.t. (9)-(11)，

[M3b] maxfC=WMfM+WDfD+WTfT+WSfS，

(15)

s.t. (3)～(8),

3 实验

3.1 实验数据

3.1.1物资收集量 本文调查上海市浦东新区一个社区的物资收集量：物资收集之初数量较少，在网络和社交平台的作用下，情感传播带动人们参与捐赠，物资量呈现快速增长，达到单位时间内收集量的顶峰.随着未参与捐赠人数的减少，单位时间内收集到的物资量下降直到为0.

图2为物资收集量图，每个时段的物资量由柱状图表示，累计物资量如曲线所示.本文采用γ分布的概率密度曲线模拟社区的物资收集量，每个社区的物资收集量是关于时间t的函数，见式(16).

(16)

其中，k为形状参数，θ为尺度参数，λ为规模参数，t表示时间(单位：h)，f(t)为t时间内收集到的物资量.令λ=1，t=40，k、θ分别取3组不同数据时得到图3.

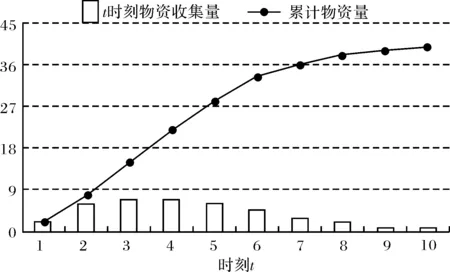
图2 物资收集量图Fig.2 Material collection graph

图3 物资收集模拟图Fig.3 Simulation figure of material collection

3.1.2 案例数据 以上海市浦东新区的37个街道办事处为单位收集物资.物资从社区到受灾点的募集流程为：各社区收集的物资运往其分配的临时收集点，临时收集点汇总物资送往汇总点，从汇总点运往受灾点.

实际案例中共涉及到4类相关数据：1)与社区相关的数据：社区到汇总点的运输时间；各社区之间的运输时间；各社区72 h内每个时间单位(1 h)内物资的收集量由式(16)算出，分别如表1和表2所示.

表1 各社区到汇总点的运输时间表(部分)

表2 社区之间的运输时间表(部分)

2)与临时收集点相关的数据：临时收集点的固定建设成本：1000，最大容量：6000.3)与汇总点相关的数据：拟送往灾区的总物资量：30000，收集物资允许的最大时间：52 h.4)物资成本数据：物资收集成本、物资转运成本和物资运输成本，分别为1、0.5、1.5)其他数据.车辆的行驶速度为30 km/h.

3.2 实验场景

本文使用Matlab R2013a软件对模型进行求解，得出最优解，得到目标函数中相应的值，如表3所示.

表3 成本值表

考虑模型中的变量值及分配给不同目标的权重值对实验结果的影响，本文设计了表4所示的5个实验.

表4 实验配置

表5 参数的敏感性分析结果

3.1.1 实验1 物资收集量、收集成本受到物资收集规模参数和时间的影响，物资收集量与规模参数的变化一致，物资量高峰出现在[0.5L，L].物资收集信息的传播能更快收集到尽可能多的物资.临时收集点的容量决定其建设数量，其数量的增加带来转运成本的增加.当其容量减少75%时，所有社区都会被选为集中点.以降低成本为目标，可以增大临时收集点容量，减少其数量，从而减少建设和转运成本.以物资收集量为目标，可以增大物资收集规模系数.可以通过宣传扩大受众范围，增加宣传成本能带来物资量的大幅度增加.

3.1.2 实验2 16h时，物资收集量少.当其权重小于0.5时，物资量基本不变，之后缓慢增长.权重为0.9时，增长速度最快.20 h时，物资量在0.5时有较快增长，0.5前后，物资量变化幅度小.物资收集前期，投入经济成本宣传能带来物资量的迅速增加，而后期应该均衡考虑经济成本与物资收集量的关系.

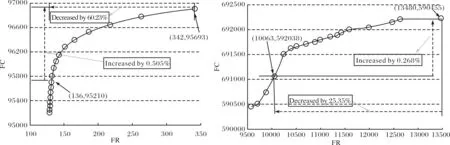
图4 16 h和20 h时的Pareto分析结果图Fig.4 Pareto analysis result in 16 h and 20 h

图5 Ti，j和Tk，1对结果的影响Fig.5 Impact of Ti，j and Tk，1 on the result

3.1.3 实验3和实验4 社区间的行驶时间越长运输成本越高，转运成本在两个端点值处波动明显.社区到汇总点的转运成本与时间成正比，而运输成本在[0.2Tk，1，1.2Tk，1]上持续增长，之后不变，且在初期增幅较大.

3.1.4 实验5 由表6可知，临时收集点容量增大，其数量和成本减小.物资收集规模系数较小时，临时收集点较少，但收集量不够.组织者应设计合适容量的收集点，运用恰当的宣传方法，在规定时间内收集到满足要求的物资.

综上所述，为减少经济成本，可以选择新型的建筑材料，改善募集点的管理方式.为增加收集的物资量，应该充分发挥宣传的作用，调动居民的积极性，争取在规定的时间内收集到尽可能多的物资.

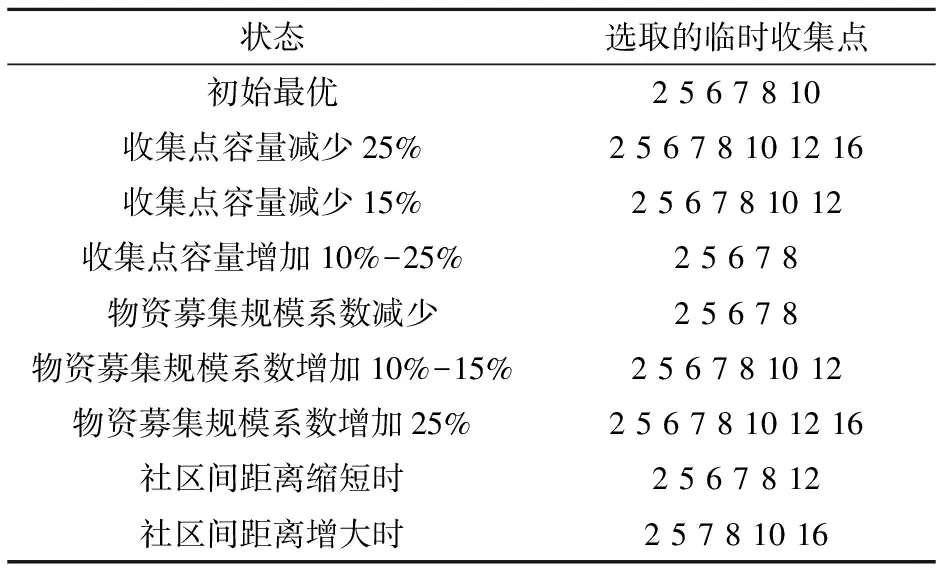
表6 临时收集点变化表

4 结论

文章以上海市浦东新区的37个市镇为例，建立双目标0-1整数规划模型，最小化经济成本并最大化收集物资量，用Matlab软件求解.调节参数，进行敏感性分析；调整两个目标的权重，进行Pareto分析.文章仍存在以下不足：采用数量计算救援物资，没有考虑物资的重量、体积等因素；采用γ分布曲线模拟社区物资的收集量，存在误差；网络情感的传播方式和影响人数没有给出定量的表达式；每个社区和城市的物资收集量，与当地的经济、人口等情况息息相关，总量应存在差别.未来的研究中，可以采用微分方程的方法，借鉴病毒、舆情等的传播方程，考虑人群、传播媒介的特征，构建不同传播渠道下的情感传播方程；根据网络情感传播方程，考虑社区的人口分布、经济状况等条件，建立每个社区的物资收集模型；记录每件物资的体积、重量等属性，增加物资运输车辆的容量和载重限制，使物资募集模型更贴近实际情况；通过实地调查、问卷采访和网络考察的方式，验证物资收集模型的可靠性，并做相应完善；最后，在物资运输阶段，将路段属性考虑在内，选择可靠性高、行驶时间短的道路进行物资运输，节约时间，提高效率.

[1] 徐 苒, 潘 郁. 地震应急物资中转站选址模型与算法[J]. 安徽农业科学, 2008, 36(30): 13473-13474．

[2] 杨 勃, 杜 冰, 李小林. 多受灾点救灾物资分配调度问题启发式算法[J]. 系统工程, 2012, 30(1): 97-103．

[3] 刘春林, 盛昭瀚, 何建敏. 基于连续消耗应急系统的多出救点选择问题[J]. 管理工程学报, 1999, 13(3): 13-16．

[4] 刘春林, 何建敏, 施建军. 一类应急物资调度的优化模型研究[J]. 中国管理科学, 2001, 9(3): 29-36．

[5] CHIERICHETTI F, LATTANZI S, PANCONESI A. Rumor spreading in social networks[J]. Theoretical Computer Science, 2011, 412: 2602-2610．

[6] 李 纲, 董 琦. Web2.0环境下企业网络舆情传播过程的研究及实证分析[J]. 情报科学, 2011, 29(12): 1810-1814．

[7] JOHNSON R, KOVCS B, VVICSEK A. A comparison of email networks and off-line social networks: A study of a medium-sized bank[J]. Social Networks, 2012, 34: 462-469．

[8] 兰月新. 突发事件网络舆情谣言传播规律模型及对策研究[J]. 情报科学, 2012, 30(9): 1334-1338．

[9] 潘 芳, 卞艺杰, 潘 郁. 危机事件网络舆情传播模型及消极思潮应急对策[J]. 图书情报工作, 2010, 54(15): 40-43．

[10] 陈 波, 于 泠, 刘君亭, 等. 泛在媒体环境下的网络舆情传播控制模型[J]. 系统工程理论与实践, 2011, 31(11): 2140-2150．

[11] ISHAM V, HARDEN S, NEKOVEE M. Stochastic epidemics and rumours on finite random networks[J]. Physica A, 2010, 389: 561-576．

[12] 潘 新. 基于社会网络的舆情传播模型构建与分析[J]. 运筹与管理, 2011, 20(2): 176-179．

[13] 朱恒民, 李 青. 面向话题衍生性的微博网络舆情传播模型研究[J]. 现代图书情报技术, 2012(5): 60-64．

[14] NEKOVEE M, MORENO Y, BIANCONI G, et al. Theory of rumour spreading in complex social networks[J]. Physica A, 2007, 374: 457-470．

[15] HAKIMI S L. Optimum locations of switching centers and the absolute centers and medians of a graph[J]. Operations Research, 1964, 12(3): 450-459．

[16] HAKIMI S L. Optimum distribution of switching centers in a communication network and some related graph theoretic problems[J]. Operations Research, 1965, 13(3): 462-475．

[17] TOREGAS C, SWAIN R, REVELLE C, et al. The location of emergency service facilities[J]. Operations Research, 1971, 19(6): 1363-1373．

[18] WEAVER J R, CHURCH R L. Computational procedures for location problems on stochastic networks[J]. Transportation Science, 1983, 17(2): 168-180．

[19] RAWLS C G, TURNGULST M. Pre-position of emergency supplies for disaster response[J]. Transportation Research Part B, 2010, 44: 512-534．

[20] 詹沙磊, 刘 南. 基于模糊目标规划的应急物流多目标随机规划问题[J]. 中国机械工程, 2011, 22(23): 2858-2862．

[21] 张 敏, 黄 钧, 朱建明. 基于失效情景的应急设施选址问题[J]. 数学的实践与认识, 2012, 42(2012):150-158.

[22] MURALI P, ORDONEZ F, DESSOUKY M M. Facility location under demand uncertainty: Response to a large-scale bio-terror attack[J]. Socio-Economic Planning Sciences, 2012, 46(78-87): 78-87．

[23] 骆正清, 苑 魁. 应急物流服务网点选址模型研究[J]. 物流科技, 2010(6): 47-50．

[24] 陶 莎, 胡志华. 需求与物流网络不确定下的应急救援选址问题[J]. 计算机应用, 2012, 32(9): 2534-2537．

[25] RATH S, GUTJAHR W J. A math-heuristic for the warehouse location-routing problem in disaster relief[J]. Computers and Operations Research, 2011, 7(16): 1-15．

[26] LIN Y H, BATTA R, ROGERSON P A, et al. Location of temporary depots to facilitate relief operations after an earthquake[J]. Socio-Economic Planning Sciences, 2012(46): 112-123．

[27] HU Z H, SHEU J B. Post-disaster debris reverse logistics management under psychological cost minimization[J]. Transportation Research Part B, 2013, 55: 118-141．

Research on location problem of social relief supplies under network emotion transmission

LI Qing1,2， HU Zhihua2

(1.School of Economics and Management， Tongji University， Shanghai 200092;2.Logistics Research Center， Shanghai Maritime University， Shanghai 201306)

Social relief plays an important role in emergency rescue. Internet speeds up the spread of information and emotion, which pools more people into materials donation activity. Community is the smallest unit of material collection, in which the materials are managed by temporary centralized point and then transported to gathering point. In this paper, a model to realize the goal of minimizing economic costs and maximizing material collection is established for determining the location of temporary centralized point. 37 streets of Pudong New Area, Shanghai City, are used as the object and the material collection model under emotion transmission is taken into consideration. Experiments are designed to analyze the parameter sensitivity, and Pareto analysis is made on the above two goals.

network emotion; social material; site selection

2015-03-28.

国家自然科学基金青年项目(71101088);国家自然科学基金面上项目(71171129); 国家自然科学基金重点项目(71390521);上海市曙光计划项目(13SG48);教育部博士点基金项目(20113121120002，20123121110004);上海市科委项目(11510501900，12510501600，12ZR1412800);上海市教委科研创新项目(14YZ100);上海海事大学研究生学术新人培育项目(YXR2014075).

1000-1190(2015)06-0883-07

F253.4

A

*E-mail: mzsq126@126.com.