幂律流体在裂缝介质中渗流特性的分形分析
2015-03-22王世芳邓永菊郑秋莎
王世芳, 吴 涛, 邓永菊, 郑秋莎
(1.湖北第二师范学院 物理与机电工程学院, 武汉 430205;2.武汉工程大学 理学院, 武汉 430074)
王世芳1*, 吴 涛2, 邓永菊1, 郑秋莎1
(1.湖北第二师范学院 物理与机电工程学院, 武汉 430205;2.武汉工程大学 理学院, 武汉 430074)
非牛顿流体在多孔介质/裂缝介质中的输运特性已成为许多应用科学及工程技术领域的研究热门问题.本文基于分形理论和广义达西定律研究了幂律流体在裂缝岩石中流动特性,得到了幂律流体在裂缝介质中总流量和有效渗透率的分形解析表达式.研究结果表明,幂律流体有效渗透率是裂缝网络结构参数和幂指数的函数.该模型计算结果与已有的模拟实验数据相比较吻合较好,证实了本模型的有效性.
裂缝介质; 分形理论; 幂律流体; 有效渗透率
多孔介质/裂缝介质广泛存在于大自然界中,譬如油气藏、页岩气藏、地下水资源、土壤等.非牛顿流体在多孔介质/裂缝介质中的流动特性吸引了石油工程师、采矿工程师、水文学者等研究人员的关注与兴趣[1-4].目前有大量的文献报道了非牛顿流体在多孔介质中流动特性.员美娟[5]基于毛细管模型和分形理论研究了卡森流体在多孔介质中的流动行为,给出了其流量、启动压力梯度和渗透率的解析表达式.同时,员美娟[6]还研究了Sisko流体在多孔介质的渗流特性,给出了流量和平均流速的分形表达式.张斌[7]通过分形理论给出了幂律流体在多孔介质中的渗透率表达式,清楚地揭示影响渗透率的物理机制.Wang[8]采用毛细管模型,利用分形理论方法计算了幂律流体在树状分叉网络的渗透率,给出了绝对渗透率及相对渗透率表达式.王世芳[3]基于广义达西定律和分形理论研究了Bingham流体在点到圆形树状分叉网络中的启动压力梯度和渗透率,分析了网络结构参数及流体特性行为参数对启动压力梯度的影响.尽管对非牛顿流体流动行为的研究文献比较多,但是他们大多数采用毛细管模型,即把多孔介质的孔隙看成是一束平行的圆形毛细管.然而,自然界中岩石裂缝往往是不规则的,不能简单地看成横截面为圆形毛细管.已有大量文献表明[9-12],岩石裂缝可以简化成一对平行平板,流体在裂缝岩石中流动看成是流体在横截面为矩形的裂缝(即平行平板模型)中流动.早在20世纪70年代,Bear[11]利用平行平板模型提出了牛顿流体在单个矩形裂缝中流动的流量表达式——著名的“Cubic Law”.然而,在大自然界和实际工程应用领域,还存在各种非牛顿流体,幂律流体就是一种常见的非牛顿流体.在石油工程领域为了提高石油开采率,往往在油气田开采时采用幂律流体灌注方式来提高其采收率.Vittorio Di Federicos[13]对Cubic Law进一步扩展,分析了非牛顿幂律流体在可变孔径单个裂缝中的流动行为,给出了其流量的表达式.后来,考虑了裂缝迂曲度之后,他利用等效裂缝孔径概念推导了幂律流体在可变孔径单个裂缝的流动控制方程[14].然而,油气藏、页岩等中裂缝网络是由无序、不规则的狭长裂缝网络构成的.已有文献表明裂缝介质(包含裂缝岩石、油气藏、矿藏、地下水资源)中裂缝宽度和裂缝数量呈幂指数关系,即岩石裂缝宽度满足分形标度律[15-17].本文主要工作是基于分形理论,提出幂律流体在裂缝岩石中的有效渗透率分形模型.
1 幂律流体在单个矩形管道中的流动
首先,考虑幂律流体在单根矩形管道沿x轴方向流动.设矩形管道上下表面均为光滑平面,它们之间间距为b(裂缝孔径为b),矩形宽度为w,如图1所示.为了简化分析问题,假设幂律流体是在一维平面内沿x轴流动,即w≥b.
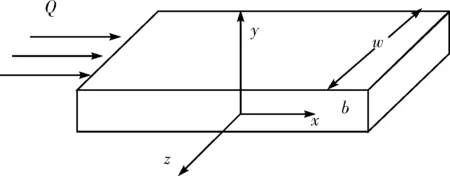
图1 管壁光滑的矩形管道结构示意图Fig.1 A sketch of a parallel plate fracture with smooth walls
由于非牛顿幂律流体在平板内沿x轴流动,其Navier-Stokes方程可以写成:
(1)
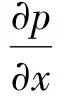
(2)
幂律流体的本构关系为:
(3)

(4)
式中,n为幂指数,C为表示流体流动行为的常数.当n<1,流体为伪塑性流体;当n=1时表示牛顿流体;当n>1 时为膨胀性流体.将方程(4)代入方程(2),可以得到
(5)
注意方程(5)的左边仅仅是y的函数,而方程(5)右边是x的函数,对方程(5)依次积分两次,分别得到:
(6)
(7)
其边界条件为
(8)
根据边界条件(8),确定出积分常数
于是,幂律流体在单个矩形管道中流速可表示为
(9)
因此幂律流体通过单根矩形管道的流量可以通过下列积分得到:
(10)
当n=1时,方程(10)可以化简成著名的“Cubic Law”,其中常数C对应牛顿流体的粘度系数;n≠1 就是非牛顿幂律流体满足的广义cubic law.
大量实验表明裂缝介质的裂缝宽度满足分形分布,裂缝宽度大于或等于w的裂缝数目为[15]:
(11)
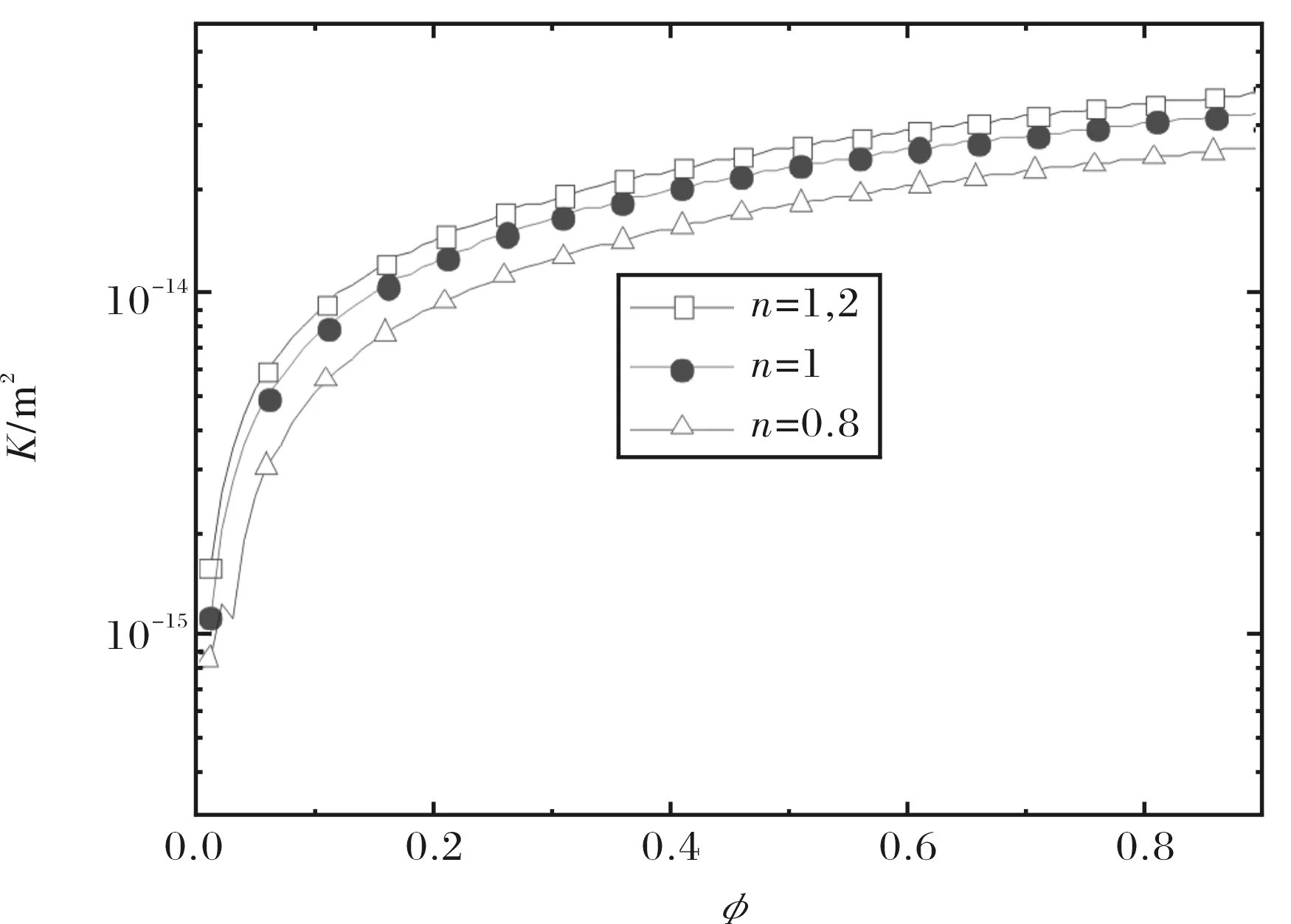
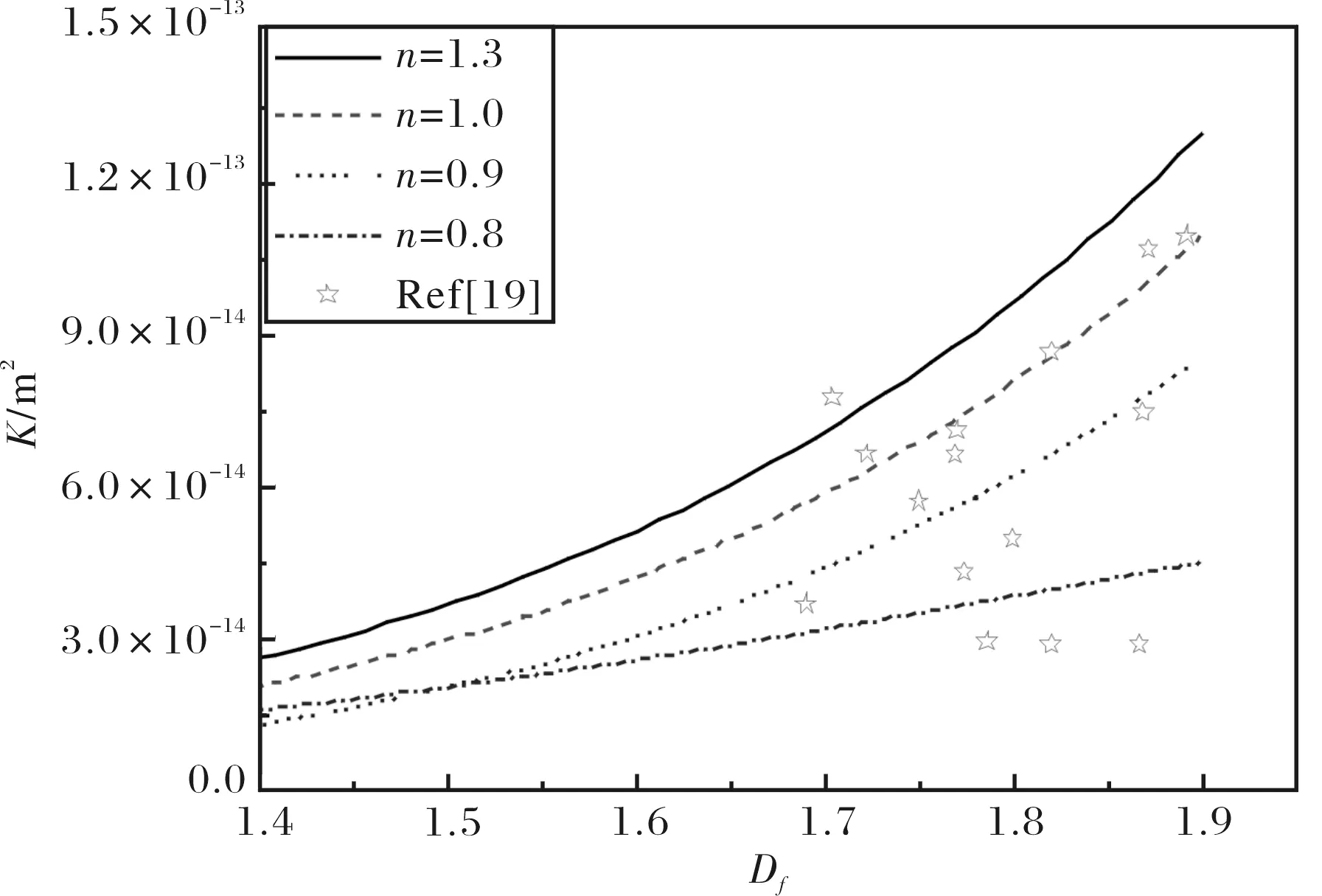
式中,Df为裂缝宽度分形维数,在二维空间,0 裂缝孔径与裂缝宽度之间满足如下关系[15,18]: b=βw. (12) 对方程(11)两边微分,得到裂缝宽度在w和w+dw之间的裂缝数目为: (13) 假设裂缝介质可以近似看作是由一束裂缝宽度满足分形分布的平行矩形管道组成,那么流过裂缝介质的总流量为: (14) (15) (15)式代表幂律流体通过裂缝介质的总流量,它是裂缝介质参数与流体特性的函数.令n=1,则(15)化简为: (16) 此表达式正是牛顿流体在裂缝介质中的流量. 牛顿流体是幂律流体幂指数n=1时的一种特例,它的流动行为较为牛顿流体复杂.幂律流体在单根矩形管道中的剪切速率为: (17) 幂律流体在单根矩形管道的平均剪切速率可以表示为: (18) 通过对(18)式积分,得到幂律流体在裂缝介质中总剪切速率为 (19) 幂律流体在裂缝介质中等效视粘度可定义为 (20) 根据幂律流体满足的广义达西定律: (21) 其中,A为裂缝介质的横截面,K为幂律流体的等效渗透率. 联立方程(21)、(20)与(14),得到幂律流体在裂缝介质中的等效渗透率: (22) (22)式表示幂律流体通过裂缝介质的等效渗透率,它是裂缝介质结构参数(wmax、wmin、Df和A)的函数,不含其它经验常数,每个参数都有明确的物理意义,清晰地揭示影响幂律流体在裂缝介质中渗流特性的物理机制. 如果令(22)式中n=1 ,则幂律流体在裂缝介质中的有效渗透率可以简化成 (23) 式(23)正是牛顿流体在裂缝介质中有效渗透率的解析表达式. 下面分析裂缝介质结构参数对幂律流体等效渗透率的影响.裂缝宽度分形维数可以由下式给出: (24) 裂缝介质单元面积为[15] (25) 图2显示了幂律流体等效渗透率在不同幂指数下随裂缝介质孔隙率变化关系曲线图.从图2可以看出:幂指数n越大,其等效渗透率越大;同时幂律流体等效渗透率还随孔隙率的增大而增大,这可解释为孔隙率越大,其在裂缝介质中的流动阻力越小,导致等效渗透率越大,这与实验事实相吻合. 图2 幂律流体在裂缝介质中有效渗透率随孔隙率的变化关系,其中β=0.002,wmin=10 μm,wmax=1 mmFig.2 The effective permeability for power law fluid in porous fractures versus the porosity at β=0.002,wmin=10 μm and wmax=1 mm 为了验证本文提出新模型的正确性,下面将渗透率模型(方程(23))与已有的模拟实验数据[19]比较.在文献[19] 中,Jafari等人所选用实验岩石样品均采自土耳其西南部地热田,他们证实了裂缝岩石满足分形分布并采用计盒数法计算了岩石样品的分形维数,同时利用商业软件(裂缝油藏建模软件,简称FRACA软件)计算了岩石样品等效渗透率.图3显示了有效渗透率随分形维数的增加而增加,这可解释为分形维数越大,裂缝网络占据的份额就越大,幂律流体的流动阻力越小,所以有效渗透率越大,这与实际情况相一致.从图3中还可以看出在新的预测等效渗透率的分形模型里,其等效渗透率随分形维数变化趋势与文献[19]模拟结果大致相同. 图3 幂律流体在裂缝介质中有效渗透率随分形维数的变化关系,其中β=0.004,wmin=10 μm,wmax=1 mmFig.3 The effective permeability for power law fluid in porous fractures versus the fractal dimension at β=0.004,wmin=10 μm,wmax=1 mm 本文基于裂缝介质为一束大小不一、满足分形分布的矩形管道假设,利用分形理论与广义达西定律,研究了幂律流体在裂缝介质中的渗流特性,推导得到幂律流体在裂缝介质中的总流量和有效渗透率的分形解析表达式,它们是裂缝网络结构参数和幂律流体流动特性的函数,各参数物理意义明确,清楚地揭示了影响幂律流体在裂缝网络中渗流特性的物理机制. [1]BERKOWITZB,HadadA.Fractalandmultifractalmeasuresofnaturalandsyntheticfracturenetworks[J].JournalofGeophysicalResearchB, 1997, 102(6):12205-12218. [2]MOUSSAR.IsthedrainagenetworkafractalSierpinskispace[J].WaterResourcesResearch, 1997, 33: 2399-2408. [3] 王世芳, 吴 涛.Bingham流体在“点到圆”形分叉网络中的启动压力梯度[J]. 华中师范大学学报(自然科学版), 2013, 47(2): 195-199. [4]YANGS,LIANG,M,YUB,etal.Permeabilitymodelforfractalporousmediawithroughsurfaces[J].MicrofluidicsandNanofluidics, 2014(7): 1-9. [5] 员美娟, 郁伯铭, 郑 伟, 等. 多孔介质中卡森流体的分形分析[J]. 物理学报, 2011, 60(2): 404-409. [6] 员美娟. 多孔介质中Sisko非牛顿流体流动特性的分形研究[J]. 华中师范大学学报(自然科学版), 2013, 47(4): 487-490. [7]ZHANGB,YUB,WANGH,etal.Afractalanalysisofpermeabilityforpower-lawfluidsinporousmedia[J].Fractals, 2006, 14(3):171-177. [8]WANGS,YUB.Analysisofseepageforpower-lawfluidsinthefractal-liketreenetwork[J].TranspPorousMedia, 2011, 85: 191-206. [9]WTSANGCFTY,TSANGCF.Channelmodelofflowthroughfracturedmedia[J],WaterResourcesResearch, 23(3):467-479. [10]KONZUKJS,KUEPERBH.Evaluationofcubiclawbasedmodelsdescribingsingle-phaseflowthrougharough-walledfracture[J].WaterResourcesResearch, 2004, 40(2):1-17. [11]BEARJ.DynamicsofFluidsinPorousMedia[M].NewYork:AmericanElsevierPubCo, 2013. [12]FOURARM,BORIESS,LENORMAND,R,etal.Two-phaseflowinsmoothandroughfractures:Measurementandcorrelationbyporous-mediumandpipeflowmodels[J].WaterResourcesResearch, 29(11): 3699-3708. [13]FEDERICOVD.Onnon-Newtonianfluidflowinroughfractures[J].WaterResourcesResearch, 2001, 37(9): 2425-2430. [14]FEDERICOVD.Non-Newtonianflowinavariableaperturefracture[J].TransportinPorousMedia, 1998, 30: 75-86. [15]MIAOT,YUB,DUAN,Y,etal.Afractalanalysisofpermeabilityforfracturedrocks[J].InternationalJournalofHeatandMassTransfer, 2015, 81:75-80. [16]JIANGG,SHIW,HUANGL.Fractalanalysisofpermeabilityofunsaturatedfracturedrocks[J].TheScientificWorldJournal, 2013, 2013:1-5. [17]BARTONCA,ZOBACKMD.Self-similardistributionandpropertiesofmacroscopicfracturesatdepthincrystallinerockintheCajonPassscientificdrillhole[J].JournalofGeophysicalResearch, 1992, 97(4): 5181-5200. [18]DEANBH.Fractalmodelingoffracturesintightgasreservoirs[M].DoctoralThesis,1996. [19]JAFARIA,BABADAGLIT.Effectivefracturenetworkpermeabilityofgeothermalreservoirs[J].Geothermics, 2011, 40(1): 25-38. The fractal analysis of the flow characteristics of the power law fluid in fracture medium WANG Shifang1, WU Tao2, DENG Yongju1, ZHENG Qiusha1 (1.Department of Physics and Mechanical & Electrical Engineering, Hubei University of Education, Wuhan 430205;2.Laboratory of Optical Information and Technology, School of Science,Wuhan Institute of Technology, Wuhan 430073) The transport phenomena in porous media/fracture medium for non-Newtonian fluid have become hot issues in many fields of applied science and engineering technology. Based on the fractal theory and the generalized Darcy law, the flow properties for non-Newtonian fluid in fracture medium are investigated. The analytical expressions of flow rate and effective permeability for the power law fluid in fracture medium are obtained. The results show that the effective permeability is a function of the microstructural parameters of fracture medium and the properties for non-Newtonian power-law fluid. The new model is verified through comparing present results to the available simulation data, and a fair agreement between them is obtained. fracture medium; fractal theory; power law fluid; the effective permeability 2015-05-06. 国家自然科学基金项目(11402081,11304235);西南石油大学油气藏地质及开发工程国家重点实验室开放基金项目(PLN1205). 1000-1190(2015)06-0872-04 O357.3 A *E-mail: flatime@163.com.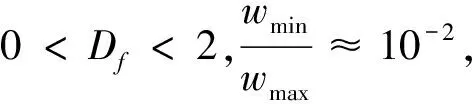
2 结果分析与讨论
3 结论
