局部引力度扩展的重叠社区发现算法
2015-03-22孙延维雷建军
孙延维, 雷建军*, 刘 倩
(1.湖北第二师范学院 基础教育信息技术服务湖北省协同创新中心, 武汉 430205;2.重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065)
孙延维1, 雷建军1*, 刘 倩2
(1.湖北第二师范学院 基础教育信息技术服务湖北省协同创新中心, 武汉 430205;2.重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065)
社交网络拥有社区结构,而网络中的一些节点又被两个或更多社区共享,这就使网络呈现出重叠社区结构.在前面对重叠社区划分算法的研究中提出了基于引力度扩展的重叠社区发现算法(GDE),以引力度最大的节点为种子来扩展与发现重叠社区.这里,提出基于h-域的局部引力度扩展的改进算法(LGDE).改进算法的实验测试结果表明该算法的执行效率获得了极大的提高,并且是可行的.
重叠社区; 局部引力度;h-域; 社交网络; 种子扩展
真实世界里的网络拥有社区结构这一重要特征,而在大多数实际的社交网络[1]中,一些社交成员都是同时参与了多个社交圈子,那么社交网络的重叠社区现象是显而易见的.学术界对挖掘网络重叠社区结构的兴趣与日俱增,目前已经出现了许多重叠社区发现算法.其中包括基于快速派系过滤的SCP算法[2],之后又有基于信息论编码理论的InfoMap算法[3],以及Blondel[4]等的层次快速展开算法等.
通过研究发现,现有的种子扩展类型的算法选取的种子具有随机性或种子在网络中的影响力较弱,这就可能使算法的社区发现效果不佳.针对此问题,在先前的研究中已提出了基于引力度扩展的重叠社区发现算法[5],其测试结果显示算法划分的社区结果的准确率有所提高,但执行效率较低,因此,本文提出改进的局部引力度扩展的重叠社区发现算法.
1 局部引力度扩展的重叠社区发现算法
给定一个无向、无权网络G(V,E),其中V是网络的节点集,E是网络的边集,节点数|V|=n,边数|E|=m;将网络中未被划分到任意一个社区中的节点的划分状态标记为‘F’,已经被分配到社区里的节点的划分状态标记为‘T’.首先,将网络中所有节点的划分状态初始化为‘F’.
1.1 基于引力度扩展的重叠社区发现算法(GDE)
基于引力度扩展的重叠社区发现算法[5]包含了有序的算法流程,其描述如下.
1)查找初始社区
步骤1:使用计算节点引力度的公式来计算网络中未被划分到社区里的节点的引力度值;
步骤2:选取引力度值最大的节点作为发现一个社区的种子;
步骤3:查询种子节点的划分状态为‘F’的邻居节点集合,这些邻居节点与种子节点便形成了一个初始社区c;
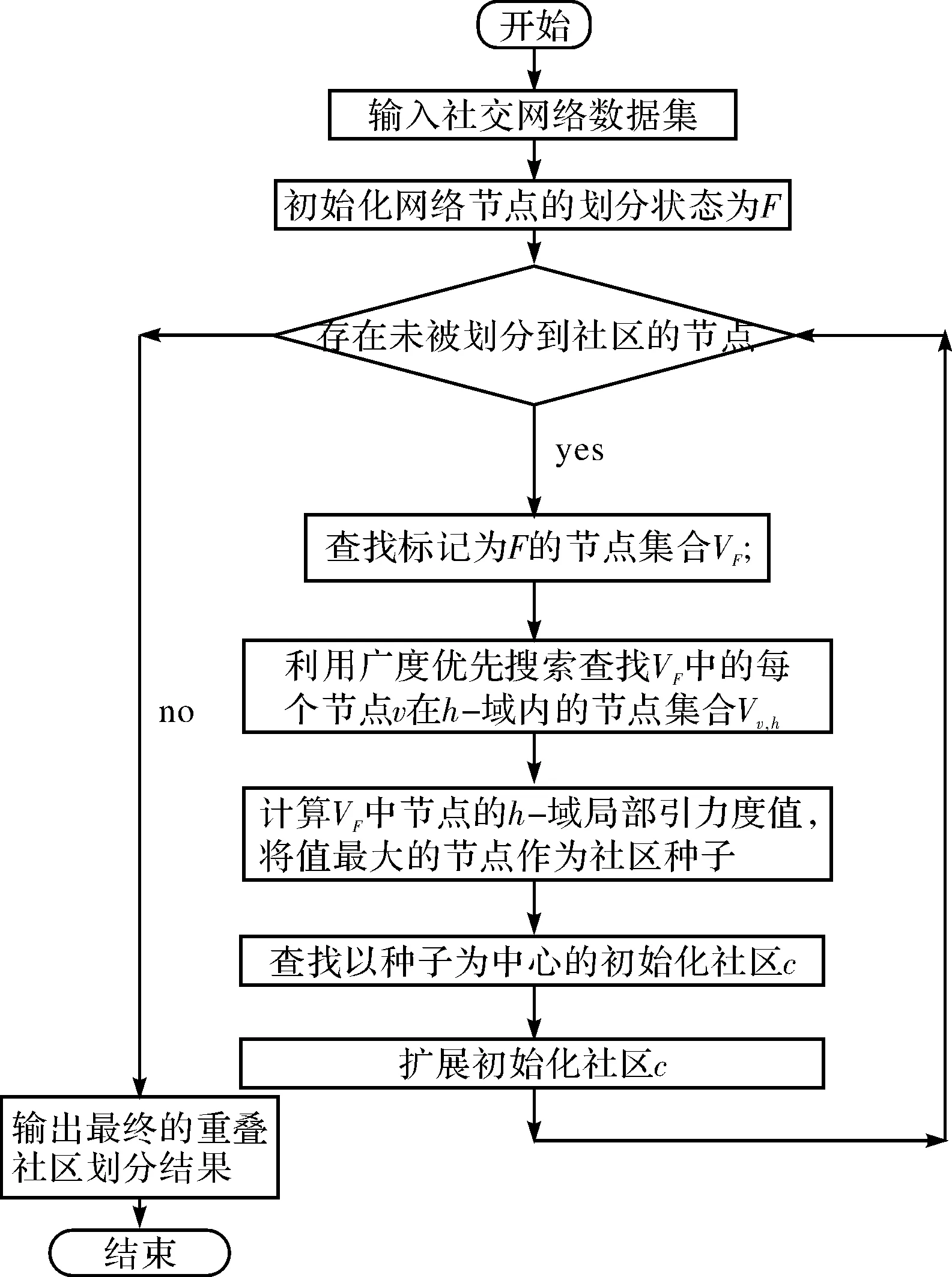
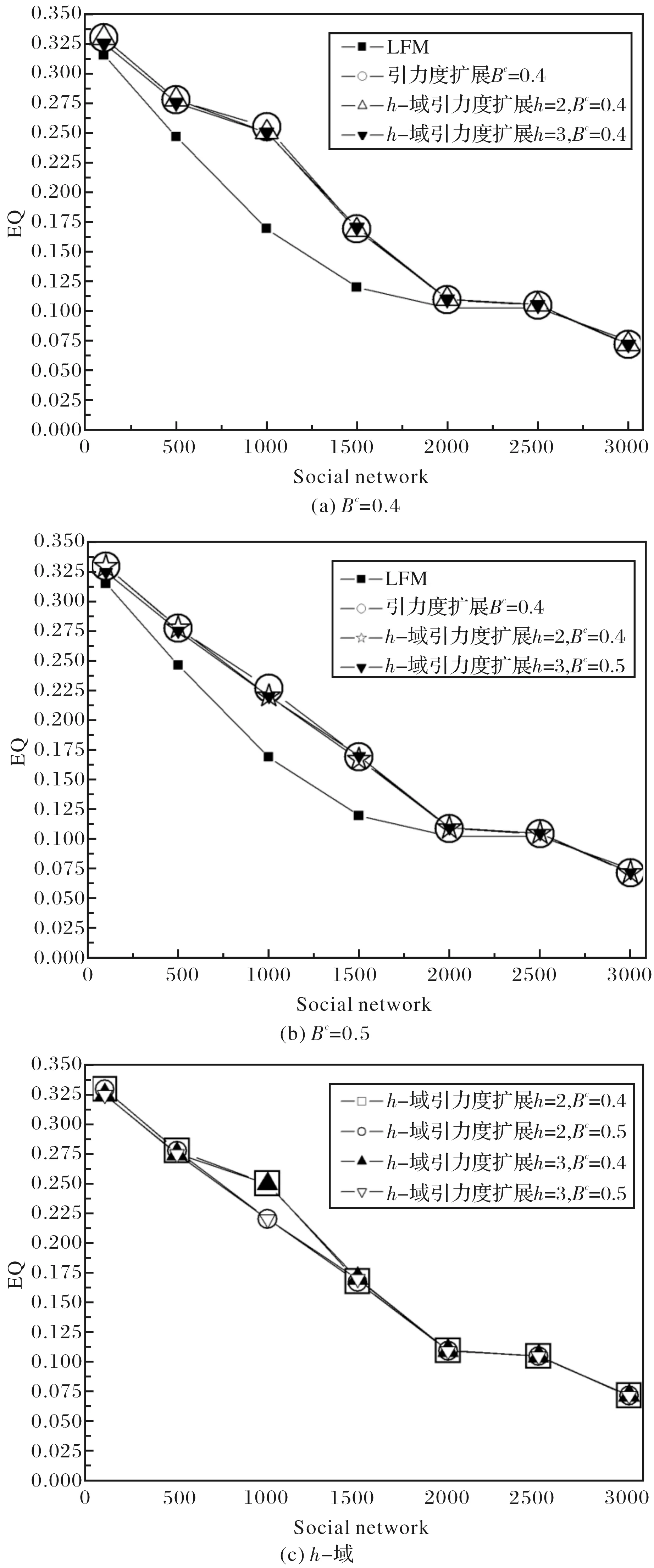
步骤4:对于社区c中的每一个节点u,计算其隶属度B(u,c)的值,如果存在B(u,c) 步骤5:返回步骤4,直到∀u∈c,B(u,c)≥Bc,则获得了最终的初始社区c. 2)扩展社区 步骤1:找出社区c的邻居节点集合,将其记为Nc,并计算邻居节点集Nc中每个节点v的隶属度B(v,c)的值; 步骤2:找出Nc中隶属度B(v,c)≥Bv(其中Bv表示节点v与社区c联系紧密程度的门限值)的所有节点,用Nv={B(v,c)≥Bv}表示这个节点集合; 步骤3:如果|Nv|>0(|Nv|表示集合Nv中节点的个数),则添加Nv中的节点到社区c中,便形成了一个更大的社区c,返回步骤1; 步骤4:如果|Nv|=0,则挖掘出了一个最终的重叠社区c. 该算法在查找初始社区的步骤1中计算节点的全局引力度值时,要计算该节点与网络中其他节点的最短路径长度,而计算网络中任意两点间的最短路径长度的时间复杂度是O(n3),则发现网络中所有重叠社区的时间复杂度就是O(n4),这会使算法的执行效率非常低下,而且通过实验表明该算法运行所耗费的时间代价确实很大. 1.2 节点的h-域 网络G的节点u的h-域表示的是包括所有通过节点u或者以节点u为起点的最短路径长度不超过h的节点集.节点u的h-域的导出子图的节点集[6]被定义为式(1): (1) 例如,图1所示的网络中,椭圆虚线圈画范围内的子图就是节点6的2-域导出子图,而节点6的2-域导出子图的节点集V6,2={1,2,3,4,5,7,8,9,10}.其中d(6,1)=2,d(2,2)=2,d(2,3)=1,d(2,4)=1,d(2,5)=1,d(2,7)=1,d(2,8)=1,d(2,9)=2,d(2,10)=2,都满足d(6,v)≤2的条件. 图1 简单的网络图Fig.1 Illustration of a simple network 1.3 节点的局部引力度 节点u的引力度就是网络中的节点u与其他节点的引力之和,这是一个全局引力度的概念,其定义为[5]: (2) 为改善算法的执行效率,我们引进节点h-域的思想将全局引力度优化为局部引力度的概念.而局部引力度的定义则为式2必须满足附加约束条件式(1),将局部引力度的公式表示为: (3) 其中,Vu,h是节点u的h-域导出子图的节点集合,Mu,Mv是网络节点u、节点v的质量,p(u,v)是节点u与节点v之间的最短距离. 1.4 局部引力度扩展的重叠社区发现算法(LGDE) 本文提出了h-域局部引力度的概念,这就使得局部引力度扩展的重叠社区发现算法在寻找初始社区时与基于引力度扩展算法在寻找初始社区的流程与思想有所不同.在此给出基于局部引力度思想下寻找初始社区的算法流程,其详细描述如下: 1)确定社区种子 步骤1:指定h-域的h大小; 步骤2:查找标记为‘F’的节点集合,将其记为VF; 步骤3:对∀v∈VF,利用广度优先搜索查找节点v在h-域内的节点集合,将其记为Vv,h; 步骤4:利用公式(3)计算∀v∈VF的局部引力度值,并选局部引力度值最大的节点为社区的种子节点,将其记为u. 2)由种子源查找初始社区 步骤1:查找种子节点u的邻居节点集,则这些邻居节点就与节点u一起组成了初始社区c,并将社区c的节点集记为Vc; 步骤2:对于∀v∈Vc,计算其隶属度B(v,c)的值,如果存在B(v,c) 步骤3:返回步骤2,直到∀v∈Vc,B(v,c)≥Bc,则获得了确定的初始社区c. 1.5 局部引力度扩展的重叠社区发现算法的流程图 图2是局部引力度扩展的重叠社区发现算法的流程图,该图清楚的描述了算法如何确定社区种子,并通过种子节点寻找初始社区,然后扩展初始社区,直到最终挖掘出网络的重叠社区结构. 图2 算法流程图Fig.2 Illustration of the algorithm process 为了测试基于h-域的局部引力度扩展的重叠社区发现算法的可行性与有效性,将算法运用在真实网络上进行了测试,并与LFM算法[7]、基于引力度扩展的重叠社区发现算法做性能上的对比. 本文提出的算法中的h为一个设置参数,在进行算法实验时,将选取h=2与h=3[6]来计算节点的h-域引力度值. 2.1 算法评价指标 2.1.1时间复杂度 时间复杂度是评价算法的时间花费代价的一个性能指标,是指执行算法所需要的计算工作,而一个算法的质量优劣将影响到算法乃至程序的效率.本文首先从理论上加以分析本算法时间复杂度,然后以本算法程序的运行时间为标准,来评估算法的执行效率. 2.1.2评价重叠社区划分质量的模块度 本文算法测试的真实社交网络数据集基本都属于无先验知识、无元数据、无类标的网络数据集.为了衡量本文算法对一个网络重叠社区结构划分质量的好坏,仍然采用文献[8]中提出的扩展模块度函数EQ(Extend Modularity)来衡量算法划分的重叠社区结构的质量. 2.2 真实网络数据集介绍 本文算法测试的网络数据集为Zachary’s karate clubshe社交网络[9]、Dolphins’s social network[10]、American College football社会网络[9]、Email网络数据集[11]与KDD Cup2012部分数据集[5].其中Karate club包括34个节点与78条边;Dolphin拥有62个节点、159条边;football包含115个节点与615条边;Email有1133个节点与5451条边.KDD Cup2012部分数据集是以一定规模增长提取的数据集,节点个数的起点为100. 2.3 社交网络的算法性能分析 2.3.1算法时间复杂度的理论分析 局部引力度扩展的重叠社区发现算法(LGDE)在计算网络节点的h-域引力度值的时间复杂度受参数h的影响,而1≤h≤n-1,其中n表示网络的规模.LGDE算法在计算网络中任意两点间的最短路径长度的时间复杂度在最优情况下是O(n2),最差情况下为O(n2(n-1)),因此,发现网络中所有重叠社区的时间复杂度在最优情况下就是O(n3),最差情况下为O(n3(n-1)).由此可见,LGDE算法的时间复杂度在最优与最差情况下都比GDE算法的时间复杂度O(n4)获得了良好的改善. 2.3.2Karate club、Dolphin、Football、Email的运行效率分析 对Karate club、Dolphin、Football、Email社交网进行了算法的真实运行时间分析,其算法的执行效率分析如表1. 表1 算法的执行效率对比表 对表1进行分析可知,LFM算法、基于引力度扩展的重叠社区发现算法、h-域引力度扩展的重叠社区发现算法在Karate club、Dolphin、Football、Email网络数据集上的运行时间随着网络规模的增大都在不断的增加.其中h-域引力度扩展算法的运行时间比LFM算法、引力度扩展算法的运行时间增加更慢,即h-域引力度扩展算法的执行效率比引力度扩展算法的执行效率获得了显著的提高. 2.3.3Karate club、Dolphin、Football、Email重叠社区划分的准确率分析 算法划分的重叠社区结构的质量优劣分析如图3.图3是算法的EQ值与Social network的关系图,横坐标表示社交网络,纵坐标表示EQ取值. 图3 Social network与EQ的关系图Fig.3 Statistics of the EQ for four social network 对图3进行分析,由图中的(a)可知,在Karate网络中,引力度扩展算法、h=2与h=3时的h-域引力度扩展算法的EQ值是相同的,且都比LFM算法的EQ值稍低.因此,LFM算法对Karate网络划分的重叠社区结构比引力度扩展算法、h-域引力度扩展算法在Bc=0.4时划分的重叠社区结构更好,且h-域引力度扩展算法划分的重叠社区结构与引力度扩展算法划分的重叠社区结构效果一样.在Dolphin、Football、Email网络中,引力度扩展算法、h=2与h=3时的h-域引力度扩展算法的EQ值基本上相同,且都比LFM算法的EQ值高.因此,LFM算法对Dolphin、Football、Email网络划分的重叠社区结构比引力度扩展算法、h-域引力度扩展算法在Bc=0.4时划分的重叠社区结构弱,且h-域引力度扩展算法划分的重叠社区结构与引力度扩展算法划分的重叠社区结构效果基本上一致. 从图3的(b)可以得出,在Karate、Email网络中,引力度扩展算法、h=2与h=3时的h-域引力度扩展算法的EQ值一样,且都比LFM算法的EQ略低.因此,LFM算法对Karate、Email网络划分的重叠社区结构比引力度扩展算法、h-域引力度扩展算法在Bc=0.5时划分的重叠社区结构质量稍微高一些,且h-域引力度扩展算法划分的重叠社区结构与引力度扩展算法划分的重叠社区结构一样准确.在Dolphin、Football网络中,引力度扩展算法、h=2与h=3时的h-域引力度扩展算法的EQ值都比LFM算法的EQ值大,即引力度扩展算法、h-域引力度扩展算法在Bc=0.5时对Dolphin、Football网络划分的重叠社区结构比LFM算法划分的重叠社区结构更加明显. 图3的(c)是h-域算法在h=2与h=3的EQ比较,h=3,Bc=0.4与h=3,Bc=0.5时,算法在Karate、Dolphin、Football、Email网络上获得的EQ值基本上分别都比h=2,Bc=0.4与h=2,Bc=0.5时获得的EQ值高;因此,h-域算法在h=3时划分的重叠社区结构比h=2时划分的重叠社区结构更加准确,质量更高,结构性更强. 2.4 KDD Cup2012数据集算法性能分析 图4是算法的运行时间Time与节点数n的关系图,横坐标为节点数,纵坐标为运行时间. 图4 节点数与执行时间的关系图Fig.4 The execution time of different nodes 由图4可以看出,随着同一网络节点数的增多,LFM算法、引力度扩展算法、h-域引力度扩展算法的运行时间都在增长.其中h-域引力度扩展算法在h=2与h=3时的运行时间比LFM算法、引力度扩展算法的运行时间增加得更缓慢,尤其比引力度扩展算法的运行时间有了数量级的减少.因此,h-域引力度扩展算法的执行效率相对于引力度扩展算法的执行效率有了极大的改善. 图5是算法实验获得的EQ值与网络节点数n的关系图,横坐标为节点数,纵坐标为EQ值. 图5 节点数与EQ的关系图Fig.5 The EQ on different nodes 在图5的(a)中可以看出,引力度扩展算法、h=2与h=3的h-域引力度扩展算法在Bc=0.4时获得的EQ值总体上比LFM算法的EQ值高,表明引力度扩展算法、h-域引力度扩展算法在Bc取0.4时划分的重叠社区结构比LFM算法划分的重叠社区结构更具有结构性,质量更高.但是,在网络规模为1000时,引力度扩展算法的EQ值比h=2与h=3的h-域引力度扩展算法的EQ值略高,说明此时h-域引力度扩展算法所划分的重叠社区结构的准确度稍微有点降低. 在图5的(b)中可以看出,引力度扩展算法、h=2与h=3的h-域引力度扩展算法在Bc=0.5时获得的EQ值总体上比LFM算法的EQ值高,表明引力度扩展算法、h-域引力度扩展算法在Bc取0.5时划分的重叠社区结构比LFM算法划分的重叠社区结构更加精确.但是,在网络规模为1000时,引力度算法的EQ值比h=2与h=3的h-域引力度算法的EQ值略高,说明此时h-域引力度算法所划分的重叠社区结构的结构性仍然有所减弱. 图5的(c)是h-域引力度扩展算法在同一网络中h=2与h=3的算法EQ比较图,当h=2与h=3,在Bc取0.5比Bc取0.4在总体上获得的EQ值稍高,但在节点规模为1000时,Bc取0.4却比Bc取0.5时的EQ值高,此时h-域算法在Bc=0.4比Bc=0.5划分的重叠社区结构质量高些.当h=3时h-域算法获得的EQ值基本上比h=2取得的EQ值高,说明h-域算法在h=3时划分的重叠社区结构比h=2时划分的重叠社区结构更强,结果更加精准. 本文提出了基于h-域的局部引力度扩展的重叠社区发现算法,将计算节点的全局引力度值优化为计算节点的h-域引力度值.然后将该算法在实际网络上进行了测试,并与基于引力度扩展算法、LFM算法做了性能上的对比分析,实验结果表明该算法在执行效率上比基于引力度扩展的重叠社区发现算法的执行效率有了显著的提高,而且该算法获得的EQ值总体上并没降低.因此,局部引力度扩展的重叠社区发现算法是有效与可行的. [1]LESKOVEJ,LANGKL,DASGUPTAA,etal.Communitystructureinlargenetworks:naturalclustersizesandtheabsenceoflargewell-definedclusters[J].InternetMathematics, 2008, 6(1): 29-123. [2]KUMPULAJM,KIVELAM,KASKIK,etal.Asequentialalgorithmforfastcliquepercolation[J].PhysicalReviewE, 2008, 2(61): 1-9. [3]ROSVALLM,AXELSSOND,BERGSTROMCT.Themapequation[J].TheEuropeanPhysicalJournal-SpecialTopics, 2009, 178(1): 13-23. [4]BLONDELVD,GUILLAUMEJL,LAMBIOTTER,etal.Fastunfoldingofcommunitiesinlargenetworks[J].JournalofStatisticalMechanics:TheoryandExperiment, 2008, 10(10): 1-8. [5] 刘 倩, 刘 群. 基于引力度扩展的叠社区发现算法[J]. 计算机工程与设计, 2014, 35(3): 110-113 [6]GREGORYS.Afastalgorithmtofindoverlappingcommunitiesinnetworks[J].EuropeanConference,ECMLPKDD, 2008, 52(11): 408-423. [7]LANCICHINETTIA,FORTUNATOS,KERTESZJ.Detectingtheoverlappingandhierarchicalcommunitystructureincomplexnetworks[J].NewJournalofPhysics, 2009, 11(33): 1-15. [8]SHENH,CHENGX,CAIK,etal.Detectoverlappingandhierarchicalcommunitystructureinnetworks[J].PhysicaA, 2009, 388(8): 1706-1712. [9]CHEND,SHANGM,LVZ,etal.Detectingoverlappingcommunitiesofweightednetworksviaalocalalgorithm[J].PhysicaA:StatisticalMechanicsanditsApplications, 2010, 389(19): 4177-4187. [10] 潘 磊, 金 杰, 王崇骏, 等. 社会网络中基于局部信息的边社区挖掘[J]. 电子学报, 2012, 40(11): 2255-2263. [11] 武志昊, 林友芳, 田盛丰, 等. 高度重叠社区的社区合并优化算法[J]. 北京交通大学学报, 2011, 35(3): 116-122. Detecting overlapping community by local gravitational degree expansion SUN Yanwei1, LEI Jianjun1, LIU Qian2 (1.Collaborative Innovation Center in Hubei Province on Basic Education and IT Services,Hubei University of Education, Wuhan 430205; 2.Chongqing Key Laboratory of Computational Intelligence,Chongqing University of Posts and Telecommunications, Chongqing 400065) Social network has community structure, with some nodes shared by two or more communities, which generates overlapping community structure. In previous work algorithms of overlapping community detection was proposed based on expansion of gravitational degree(GDE), which expanding and finding overlapping communities according to a node with maximal gravitational degree. Here we present an improved algorithm by local gravitational degree expansion based onh-region (LGDE). The experimental results demonstrated that this algrorithm is feasible and its execution efficiency has been raised. overlapping community; local gravitational degree;h-region; social network; seed expansion 2015-04-22. 湖北省教育厅科学研究中青年人才项目(Q20153001). 1000-1190(2015)06-0851-06 TP393.0 A *通讯联系人. E-mail: 756652665@qq.com.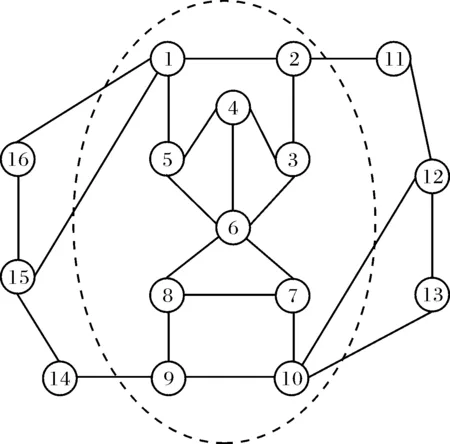
2 实验分析



3 总结
