基于航班延误的飞机和乘客恢复模型

姜 茂， 韩晓龙

(上海海事大学 科学研究院， 上海 201306)



姜 茂*， 韩晓龙

(上海海事大学 科学研究院， 上海 201306)

航班发生延误时，需要采取有效恢复措施降低航空公司的经济和信誉损失.本文利用现有飞机资源，对飞机和乘客进行合理的调度安排问题建立了飞机和乘客恢复混合整数规划模型.模型考虑了乘客的航班取消成本、航班延误成本、座舱降级成本、飞机的非正常降落位置的惩罚成本及飞机飞行成本等，以使航班恢复成本最小化为目标.对航班恢复成本进行细分，更接近航空公司在进行航班恢复时的实际情况.使用法国某航空公司真实航班数据作为算例，以验证模型的有效性和实用性.算例显示优化模型相对于航班取消方案和航班顺延方案分别使恢复成本降低了21.05%和21.46%.因此，模型能有效地解决航班航空公司飞机和乘客恢复问题，提高航空公司竞争力.

航空运输； 航班延误； 混合整数规划； 航班和乘客恢复

恶劣的天气、飞机故障、机组成员自身的身体不适等原因都有可能导致航班的延误，如果航班延误没有得到及时快速的处理，将会影响到整个航空公司的运作、收益、决策效率和乘客的满意度等.航班延误发生时，航空公司必须调整航班计划，比如延迟航班，取消航班，重设飞机路线，重新指派机组成员或召集新的机组，重新安排旅客等，如何以可行的、费用最少的恢复方案使航班恢复到原来的运行计划是航空公司面临的主要问题.航班延误的恢复问题主要包括飞机、乘客、和机组的恢复.

在航班发生延误时对飞机恢复方面，Eggenberg N， Bierlaire M， Salani M[1]对时空网络模型进行了深度扩展，解决以实现最小化总恢复时间和总恢复成本为目标的多目标整数规划问题，并引入了飞机维护约束，将列生成算法和网络算法结合起来，寻求新的恢复计划.乐美龙，马彬[2]针对飞机路线受中断情况，将飞机路线恢复问题转化为基于时间段的网络模型，以最小化航班延误成本和取消成本为目标，结合飞机流平衡约束，较好地解决了飞机路线恢复问题.唐小卫，朱金福，高强[3]则放宽了飞机流平衡的约束，加入了合并航班的恢复策略，提出了贪婪随机模拟退火算法以解决流不平衡条件下的大规模飞机恢复问题.赵秀丽、朱金福等[4]构建了以延误时间最短或延误成本最小为目标函数的飞机恢复模型，在延误成本构成中提出了旅客失望溢出成本和失望溢出率的概念，并在实际调查的前提下对旅客失望溢出率函数进行了拟合.

旅客作为航空公司的主要服务对象，在恢复过程中必须予以考虑.L. Lettovsky[5]考虑了航班恢复过程中旅客的航班取消成本、餐饮及住宿成本，并估计了航班延误对航空公司带来的信誉损失成本.Eggenberg等[6]提出了旅客流恢复网络模型，减少旅客行程取消的数量.白凤，朱金福，高强[7]为每一架可用的飞机构建时空恢复网络，把旅客恢复问题简化为多商品最小费用流问题，在求解模型时用到了列生成算法和分支定界法.D. Clarke[8]建立了一个乘客流模型，其目标函数是最大化乘客收益，但作者认为应先考虑航班恢复，然后在此基础上考虑乘客恢复.王莹，朱金福[9]在已获得航班恢复方案和航班容量为剩余座位数的限制等假设前提下，通过构建时空网络，建立了不正常航班旅客流恢复模型，并设计了Danzig-Wolfe分解算法进行求解，给出了旅客恢复方案.

在飞机、旅客和机组综合恢复方面，Niloofar Jafari[10]在其定义的恢复范围内，研究了飞机和乘客的同时恢复模型.Karine Sinclair等[11]针对轴辐式航线网络中的航班恢复提出了一种改进的大规模邻域搜索算法，包括航班重设，航班修正和航班改进三个过程.乐美龙，王婷婷等[12]建立了基于时空网络的多机型航班恢复模型，在不正常航班发生时，利用机场的多机型资源，进行调机，以达到使航空公司损失最小的目的.Bratu等[13]在综合恢复中考虑了备用机组，文章对乘客成本和航班成本做了一个权衡，模型描述了乘客的行程和航段之间的关系，目标函数是获得最大利润和提高客户满意度.赵秀丽[14]建立了航班、飞机、机组和旅客恢复的一体化模型，将航班恢复问题定义为主问题，将飞机、机组和旅客恢复定义为子问题.乐美龙，李晓岚[15]在飞机和旅客流恢复的基础上加入了机组指派和时间约束，并考虑了备用机组，目标函数是最小化飞机和机组恢复成本、最小化旅客总延误成本.

根据航空运输的实际情况，飞机上设置了不同的座舱等级，如头等舱、商务舱和经济舱.座舱等级不同的乘客机票成本也不相同，导致在航班恢复过程中乘客行程的取消成本，座舱降级成本，航班延误成本都不同.此外，国际航空公司必须考虑航班延误对出入境乘客的不同影响.上述文献在旅客行程恢复或综合恢复中只是将每架飞机上的乘客视为一个整体，在恢复过程中没有考虑不同航班类型上各座舱等级的位置数量约束和座舱降级成本，也没有考虑国际航班恢复过程中出入境乘客恢复成本的异同.只有对这些成本进行细分，才能更好的选择恢复方案，践行为旅客服务的宗旨，从而让航空公司又好又快的发展.

本文综合考虑了基于航班延误的飞机和乘客恢复模型，主要贡献包括两方面：1)在乘客恢复方面，进行了细致的成本划分，针对3种不同的航班：洲际航班，洲内国际航班和国内航班，两种不同的乘客：入境乘客和出境乘客，3种不同的座舱级别：头等舱、商务舱和经济舱，进行了细致的恢复成本划分.包括航班取消成本，航班延误成本，航班座舱降级成本； 2)在飞机恢复方面，除了考虑恢复期内对飞机的各种条件限制，如飞机定期检查维修限制、飞机里程限制等之外，为了避免恢复期内的飞机调度对恢复期结束后航空公司正常运营的影响，还考虑了恢复期结束后受影响的各机场对不同机型的飞机数量需求约束，可以避免航班延误恢复期结束后对多航空公司后续运作的影响.

1 问题描述

航班延误对飞机和乘客的影响可由图1表示，图中展示了一个由7个航班和3架飞机组成的航线网络，横轴代表时间，纵轴代表飞机.每一个航班用一条粗线代替，开始与结束的粗线分别代表航班的出发和到站时间以及机场.线下方括号里的字母代表乘客的行程.如图1所示，航班f1从机场G出发，到达机场H.航班f1结束后飞机A执飞航班f2，行程P1的旅客衔接至下一个航班f4.

图1 航班延误对乘客和飞机的影响Fig.1 Flights delay effects on passengers and aircrafts

当航班f1和航班f3延误时，要用到航班f1和航班f3执飞飞机的下一个航班以及相关的乘客都将受到影响.行程为P1的乘客有两个航班，f1和f4，当航班f1发生延误，乘客到达航班f4的始发机场H时，航班f4已出发，他们的行程被扰动了.因为飞机A发生了延误，而航班f2必须满足飞机的最小过站时间限制才能出发，所以航班f2会被延误.又因为行程为P2的旅客需要足够的登机时间衔接到航班f7，所以航班f7会受到扰动.航班f3发生延误时，若不改变航班计划，行程为P3的乘客会错过接下来的航班f6和f7，行程P3被扰动.

这个例子表明航班延误对乘客和飞机的连锁反应，也表明同时恢复飞机和旅客的必要性.本文研究的问题是同时解决航空公司最贵的飞机资源和为航空公司带来收益的旅客资源.

2 模型构建

2.1 集合

2.2 参数

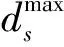
2.3 决策变量

2.4 目标函数

(1)

2.5 约束条件

(2)

(3)

(4)

(5)

(6)

(7)

taf=tdf+DTf，∀f∈F,

(8)

(9)

(10)

(11)

(tdIT(p，n)-taIT(p，n-1)-u)*yp≤0，∀p∈P,

(12)

(tdIT(p，n)-taIT(p，n-1)-u)*(1-yp)≥0，

∀p∈P,

(13)

(14)

式(2)表示各航班弧最多由一架飞机执飞，xijf表示由飞机f执飞航班弧ij；式(3)是飞机定期检查维修约束；式(4)和式(5)表明在规定时间段内，起飞和降落飞机数量不得超过机场所允许的起飞和降落数量；约束(6)表明在整个恢复期结束后，为不影响航空公司的后续运营，各机场对不同机型数量需求的要求；式(7)表明各飞机所执飞的航班飞行距离均不能超过其最大航程；式(8)表示受干扰航班的实际降落时间等于航班实际起飞时间与实际飞行时间之和；式(9)表示受干扰航班的实际起飞时间等于计划起飞时间与航班延误时间之和；约束(10)确保恢复过程中被调配给某飞机的各类座舱的乘客数与原来该飞机上所有的各类座舱乘客数之和小于该飞机的乘客容量；约束(11)确保受干扰乘客不被分配给一个中间有取消航班的行程；约束(12)、(13)确保行程p之间的航班有足够的过站时间；式(14)是决策变量取值范围约束.

3 算例

该算例是来自法国一家航空公司的真实数据，包括15个航班，其中国内航班2个，洲内航班9个，洲际航班4个；包括6个机场，3个国内机场，3个国外机场；旅客行程2 729个，其中需要转机的乘客行程200个，航班与旅客行程时段网络图如图2所示.

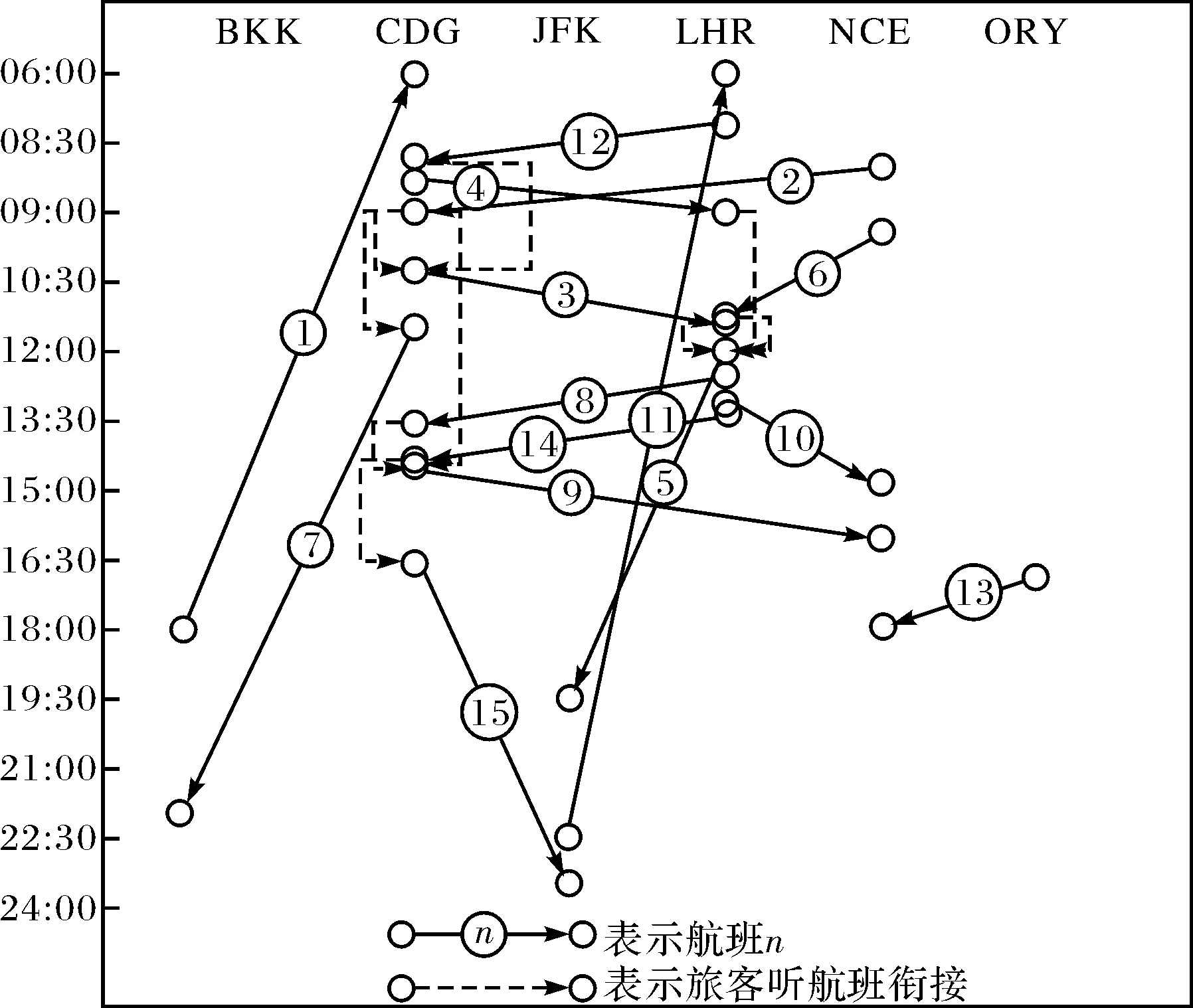
图2 航班与旅客行程时段网络图Fig.2 Time-band network of flights and itineraries

机场间的距离及不同机场间的航班类别如表1所示，其中I表示跨洲际航班，C表示洲内航班，D表示国内航班.

表1 机场间的距离及航班类别

部分旅客行程信息如表2所示，其中A表示入境乘客，R表示出境乘客，F、B与E分别表示头等舱、商务舱与经济舱.

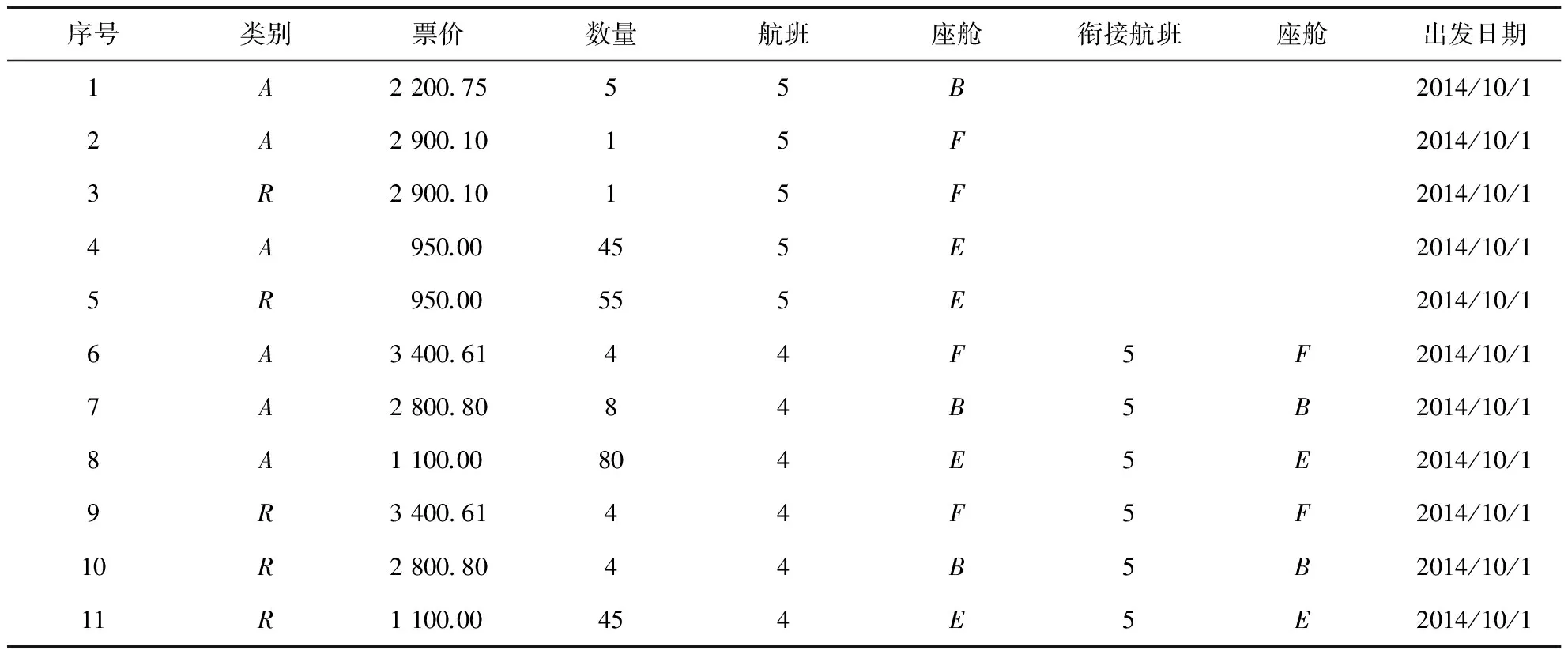
表2 部分旅客行程信息

续表2

由于特殊原因，航班3延误了1 h，导致该由该飞机执飞的航班8和航班9无法按原定计划执行，并且导致部分乘坐航班3的旅客无法按时衔接到航班5.

通过CPLEX优化软件进行求解，运行时间为3.5 min，经过调整后的具体航班恢复方案如表3所示.

表3 航班延误的恢复方案1

即将原本由飞机A320#1执飞的航班8和航班9改由飞机A320#2准点执飞，而飞机A320#1则准点执飞原本由飞机A320#2执飞的航班10，航班5则顺延1 h.恢复成本如表4所示.

表4 方案1航班恢复成本

经过模型优化后的恢复成本为33 156欧元，其中航班5顺延1 h，等待来自航班3的衔接乘客，顺延成本为30 156欧元，飞机在不影响航空公司恢复期结束后的正常运营条件下，非正常降落位置的惩罚成本为3 000欧元.

相比两种手动恢复方案，一、取消方案：若直接取消来自航班3的行程衔接乘客，航班8、9和航班10交换执飞飞机后准点执行，则取消成本为39 000欧元，恢复总成本为42 000欧元；二、顺延方案：若直接采取航班顺延的方法，即由飞机A320#1执飞的航班8和航班9顺延，航班10仍由飞机A320#2准点执飞，则总延误成本为42 216欧元，优化模型分别使恢复成本降低了21.05%和21.46%，如图3所示.

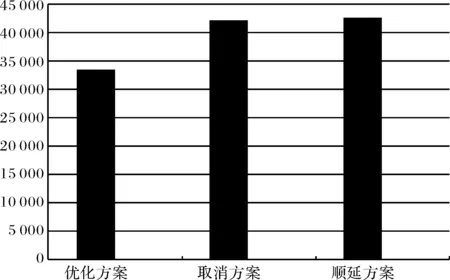
图3 恢复方案成本对比Fig.3 Cost Comparison between Different Recovery Schemes

综上所述，本文所建立的优化模型同时解决了航班发生延误时乘客与飞机的恢复问题，并取得了良好的经济效果.

4 结语

在航班发生延误时，以恢复成本最小为目标函数，综合考虑了飞机和乘客的恢复.在考虑飞机恢复的过程中，不仅考虑了如何调度现有飞机资源，进行合理的乘客与飞机的一体化调度，还考虑了在恢复期结束时，航空公司对飞机位置的要求，即恢复期结束后，后续航班上的乘客行程不至于受航班恢复过程的影响.在考虑乘客恢复的过程中，充分考虑了乘客的延误成本，座位降级成本.此外，对不同的航班，如国内航班，洲内国际航班和跨洲际航班上的乘客恢复成本进行细分，与实际情况相符，并取得了良好的恢复效果.此外，本文只考虑了航班延误恢复一种情况，未考虑机场关闭，飞机故障等其它条件下的航班、乘客恢复，且尚未考虑机组的约束条件及恢复成本，这些将是我们进一步的研究方向.

[1] EGGENBERG N， BIERLAIRE M， SALANI M. A colume generation algorithm for disrupted airline schedules [R]. Lausanne: Ecole Polytechnique Fédérale de Lausanne， 2007．

[2] 乐美龙， 马 彬. 基于时间段网络模型的飞机路线恢复研究[J]. 武汉理工大学学报， 2012， 34(11): 63-68．

[3] 唐小卫， 朱金福， 高 强. 流不平衡条件下飞机恢复的优化模型与算法研究[J]. 小型微型计算机系统，2010， 31(04):793-796．

[4] 赵秀丽， 朱金福， 郭 梅. 不正常航班延误调度模型及算法[J]. 系统工程理论与实践， 2008， 28(4): 129-134．

[5] LETTOVSKY L. Airline operations recovery: An optimization approach[D]. Atlanta: Georgia Institute of Technology， 1997．

[6] EGGENBERG N， SALANI M， BIERLAIRE M. Constraint-specific recovery network for solving airline recovery problems [J]. Computers & Operations Research， 2010， 37(6): 1014-1026．

[7] 白 凤， 朱金福， 高 强. 基于列生成算法的不正常航班调度[J]. 系统工程理论与实践， 2010， 30(11): 2036-2045．

[8] CLARKE M D. Development of heuristic procedures for flight researching in the aftermath of irregular airline operation[D]. Massachusetts:Massachusetts Institute of Technology，1998．

[9] 王 莹， 朱金福. 基于Danzig-Wolfe算法的不正常航班旅客流恢复问题[J]. 武汉理工大学学报(信息与管理工程版)， 2013， 35(4):551-554+579．

[10] JAFARI N， ZEGORDI S H. Simultaneous recovery model for aircraft and passengers [J]. Journal of the Franklin Institute， 2011， 348 (07): 1638-1655．

[11] SINCLAIR K， CORDEAU J-F， LAPORTE G. Improvements to a large neighborhood search heuristic for an integrated aircraft and passenger recovery problem [J]. European Journal of Operational Research， 2014， 233(1): 234-245．

[12] 乐美龙， 王婷婷， 吴聪聪. 多机型不正常航班恢复的时空网络模型[J]. 四川大学学报(自然科学版)， 2013， 50(3): 477-483．

[13] BRATU S， BARNHART C. Flight operations recovery: new approach considering passenger recovery [J]. Journal of Scheduling， 2006， 9(3) : 279-298．

[14] 赵秀丽. 航空公司不正常航班恢复模型及算法研究[D]. 南京：南京航空航天大学， 2010．

[15] 乐美龙， 李晓岚. 飞机和旅客流一体化恢复模型[J]. 工业工程， 2013， 16(5): 113-119.

The recovery model of aircrafts and passengers based on flight delay

JIANG Mao， HAN Xiaolong

(Scientific Research Academy， Shanghai Maritime University， Shanghai 201306)

When flight delay occurred, it will bring huge economic and reputation losses to airlines if effective measures are not performed by managers to deal with it. The mathematical model established in this article mainly aims at making full use of the existing aircraft resources and performing reasonable scheduling of aircrafts and passengers when flight delay occurred. The objective function focuses on minimizing recovery cost which included cost of flights cancellation, flights delay, Seat degradation of passengers, penalty for wrong locations and aircrafts. The recovery cost was subdivided to make it closer to the real situation. Real flight data of a French airline as an example was used to verify the validity and practicability of the model. The example shows that the optimization model with respect to the cancellation scheme of flights and postponement scheme of flights costs were reduced by 21.05% and 21.46% respectively. Therefore, the model is able to effectively solve aircraft and passengers recovery problem and improve the competitiveness of airlines.

air transport; flight delay; mixed integer programming; flight and passenger recovery

2015-03-15.

上海市科委项目(11510501900)．

1000-1190(2015)06-0876-07

F560.1

A

*E-mail:jiangmao8880@163.com．