多模态图像匹配的FFT梯度相关算法

咸艳霞, 胡修兵, 郑 莉

(1.武汉科技大学 理学院, 武汉 430081; 2.武汉大学 测绘学院, 武汉 430079)



咸艳霞1*, 胡修兵2, 郑 莉2

(1.武汉科技大学 理学院, 武汉 430081; 2.武汉大学 测绘学院, 武汉 430079)

多模态图像匹配是各领域图像匹配研究中的一个热点和难点问题,特征的可重现探测和非线性优化搜索,分别是基于特征和基于区域的多模态图像匹配的瓶颈问题.将灰度图像转换为复数域的梯度图像,提出以复数平方图像实现的2倍梯度差角余弦作为相似性测度,提出FFT梯度相关算法,实现了多模态图像局部匹域的快速匹配,通过红外与可见光图像的匹配实验,验证了算法的有效性.

多模态图像匹配; 梯度相关; 快速傅立叶变换; 共轭复数; 红外图像

图像匹配主要分为基于特征和基于区域的两类方法.基于特征的方法,通过特征描述[1]或利用特征之间的空间距离[2]或分布关系[3]进行匹配.特征匹配的优势是可以不依赖匹配初值,允许图像之间存在一定程度的几何变形,而且速度较快、稳健性较好.但对于多模态图像,特征匹配却面临很大挑战.虽然出现了许多针对多模态图像的改进算法,但这些方法一般将研究重点放在特征相似性测度的模态不变性问题上,另一个更关键的问题往往被忽略了,那就是特征的可重现探测问题[4].如果在两幅图像上探测到的特征的重现率非常低,那么特征匹配可靠性的前提就难以保证了.在基于区域的多模态图像匹配方法中,一般采用互信息[5]、梯度[6]、自相似性[7]等作为相似性测度.这些方法在医学、计算机视觉和遥感等领域都有成功的应用,但计算量大和局部极值等问题还很难克服.

本文提出结合FFT(快速傅立叶变换)的梯度相关算法,属于区域匹配的类型,所以不必受限于特征提取的效果.区域匹配的主要限制是对图像几何变形的适应性较差,好在许多应用场合图像之间的摄影姿态关系是已知的,因此整体的图像变形是可以纠正的.纠正以后匹配的搜索空间是二维平移变换,通过将FFT与改进的梯度相关算法结合,速度显著提高,因此可以采用穷尽搜索,从而无需采用非线性优化算法而不受局部极值的影响.必要时还可以在局部匹配的基础上,对图像进行更高精度的几何纠正,再进行匹配以获取更高的匹配精度.

1 基于梯度差角余弦的匹配测度

由于多模态图像灰度特性的非线性改变,灰度相关已不能适用,利用梯度信息是多模态图像匹配的重要方法之一.梯度的幅值会因灰度特性差异而发生改变,而梯度的方向则有较好的稳定性.

匹配测度可以看作概率估计问题.在某种基于梯度的匹配测度下,如果匹配区域的梯度全部为0(无任何结构信息)时的测度值为0,则两块无关区域(结构无关)的匹配测度值的概率期望值也应该为0,这样的估计才是无偏的.两个单位向量的内积即等于差角的余弦,文献[6]以归一化梯度的内积平方和最小作为匹配测度,避免了烦琐的三角函数计算,但余弦函数平方的概率估计为1/2,其估计是有偏的.文献[8]采用了内积与外积的绝对值之差作为改进的匹配测度,是一种无偏估计,但这两种方法都无法结合FFT快速算法.由于梯度信息主要分布在边缘附近,因此梯度匹配的拉入范围较其它区域匹配方法的拉入范围更窄,因此要求有较好的匹配初值并依赖非线性全局优化算法.所以其匹配效率与常用的互信息方法相比并没有明显优势.文献[9]将梯度角度当作灰度来构造图像,借用FFT灰度相关算法实现多模态图像的快速匹配,但由于角度是周期性的,尽管采用了“准梯度”来修正其影响,但是在模型上依然是不严谨的.

对于单模态图像,余弦函数是利用梯度方向评价匹配相似性的一种理想测度.如图1所示,其中θ′是对应点梯度方向角之差,余弦函数是偶对称的,且概率期望值为0,这些性质很适于评价梯度方向的差异程度.

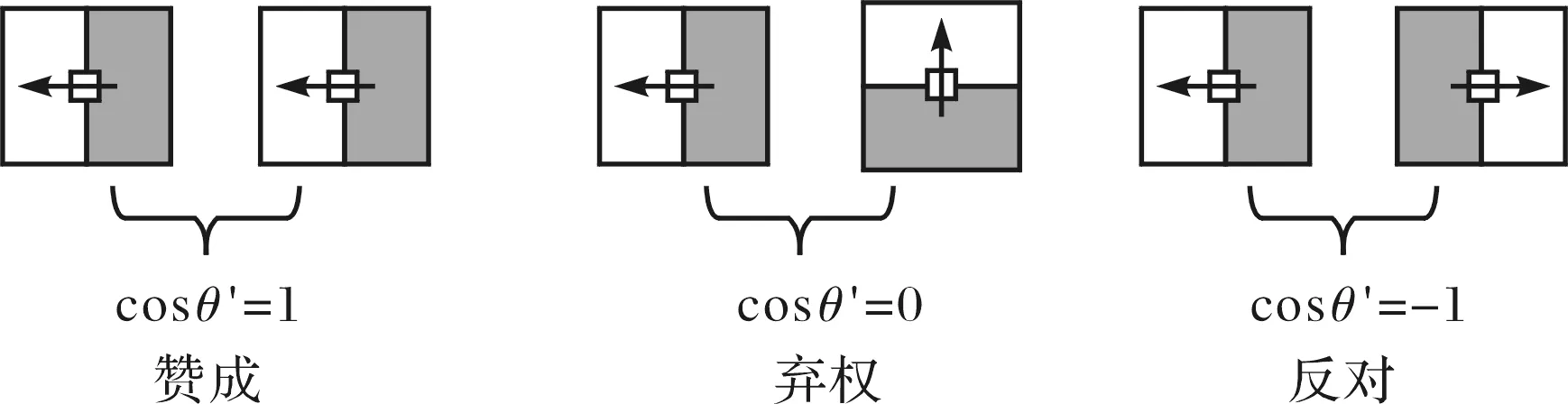
图1 单模态图像的梯度方向余弦测度Fig.1 Cosine measure of monomode image gradient

多模态图像之间的对比度反转是不确定的(例如图5可见光与红外图像的灰度对比关系).所以梯度方向相同和方向相反的情况,对匹配测度评价都应该是正贡献的[8].

图像的梯度可以用复数表示,通过求取垂直和水平两个方向的梯度再组合而成,复数还可以表示成幅度(模)和角度的形式,分别表示梯度的强度和方向:

c=x+yi=reiθ=rcosθ+i·rsinθ.

(1)

本文提出的方法是先求取复梯度平方图像,因为单位复数的平方的结果即为方向角加倍,即

c1·c2=r1eiθ1·r2eiθ2=(r1·r2)·ei(θ1+θ2).

(2)

角度加倍后,余弦函数的周期减半,以其作为匹配测度在模型上更贴近多模态图像匹配的特点(如图2).

图2 多模态图像的梯度方向余弦测度Fig.2 Cosine measure of multimode image gradient

2倍角余弦的概率期望值也为0,以其作为多模态图像匹配测度估计具有无偏性.通过复数平方运算方便地实现了2倍角余弦计算,结合FFT频域处理技术,可以快速实现多模态图像的局部区域匹配.

2 结合FFT的梯度相关算法

空间域复杂的相关或卷积运算,可以转换为频率域的简单乘法运算,而空间域与频率域的转换又可以用FFT快速实现,利用频域变换处理图像区域匹配可以实现数量级意义上的效率提升[9-10].

两个复数共轭相乘的结果即为幅度相乘、角度相减,而复数的实部和虚部分别为复向量的余弦分量和正弦分量.所以复数共轭乘积的实部即为:

(3)

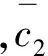
3 图像的投影纠正处理

将图像纠正处理为与基准图像相同的拍摄角度,一方面增强图像区域之间的可匹配性,另一方面可以降低匹配搜索的维度,便于结合频域处理算法,以提高匹配效率.

如图3所示,目标场景和摄影中心不变,仅转动相机的摄影方向.由于在物方空间坐标系下,纠正前后的像点位置、摄影中心、和目标点4点是共线的,投影纠正处理就相当于对原影像点(x,y,-f)T重新拍摄成像.设旋转矩阵为:

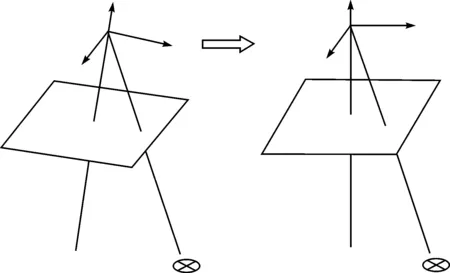
图3 投影纠正处理中的像点坐标变换关系Fig.3 Image coordinate transformation of perspective correction processing

由共线方程[11]就可以得到摄影纠正的坐标转换公式:

(4)

其中,F是基准图像的焦距,因此纠正后图像与基准图像有相同的缩放比例.

综上所述,本文提出的FFT梯度相关算法的流程如图4所示.

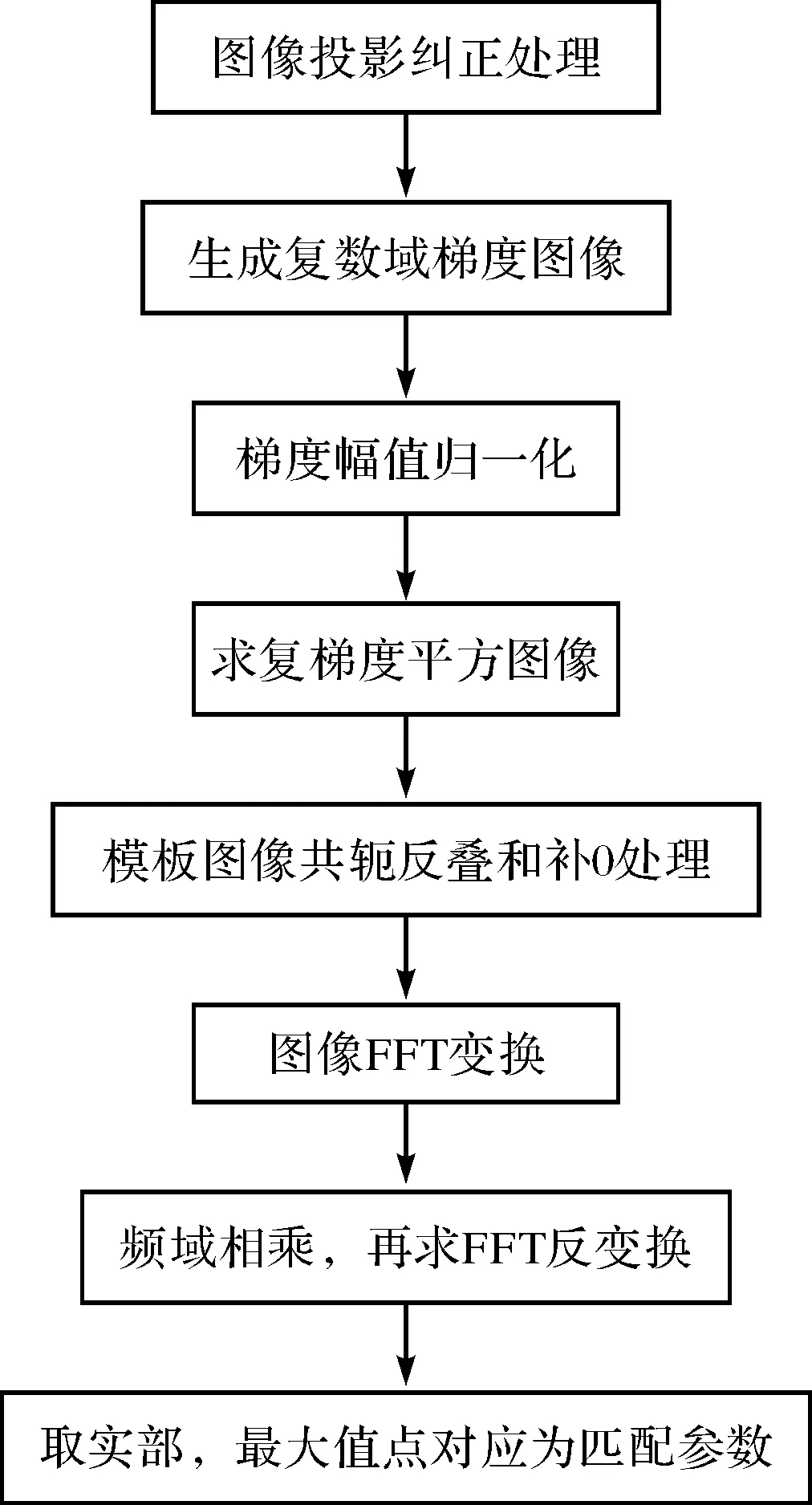
图4 多模态图像匹配的FFT梯度相关算法Fig.4 The FFT gradient correlation algorithm for multimodal image matching

4 实验与分析

实验图像是从同一地点拍摄的可见光和红外图像(图5),大小分别为2400×3200和512×640像素,摄影方向基本一致,无需做投影纠正处理,几何关系近似为相似变换.

4.1 整体匹配实验

由摄影焦距和像素大小,可以估算出两幅图像的缩放比例约为0.45,经过缩放调整再匹配应该能找到红外图像对应于可见光图像中的位置.

图5 同一地点拍摄的红外与可见光图像Fig.5 Visible and IR images acquired from the same position

利用Matlab实现本文提出的FFT梯度相关算法,解得位移参数,两幅图像套合的效果如图6左所示.由于拍摄时图像之间有微小旋转,并且缩放比例估计得也不够精确,所以套合的效果还不够理想.

图6 图像纠正前、后匹配套合的效果图Fig.6 Renderings of nested images before and after the rectifications respectively

将红外图像等分成4块,分别与可见光图像匹配,得到4块子图像的位移参数.由任意两块子图像的位移量就可以解算出相似变换参数,分别采用两个对角方向的两对子图像解算,再取平均值,得到更精确的旋转角0.755度和缩放比0.442,对可见光图像纠正后,再匹配的套合效果如图6右所示.

图7为图像纠正前、后的梯度相关测度值的分布图,峰值分别为0.081和0.178,从图中还可以看出纠正以后匹配峰值的显著性更好.经过测试,本文方法对图像旋转的适应能力达3度以上,如果未纠正的图像旋转角度较大,可以以5度为步长对模板进行旋转重采样,仍次进行快速匹配,取匹配测度的最大值即可,仅需要匹配两对同名点,就可以较精确地纠正图像的旋转变形.

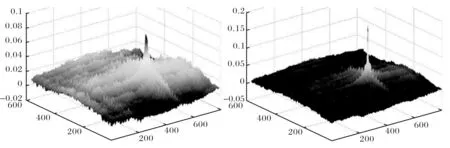
图7 图像纠正前、后匹配测度值的分布图Fig.7 Renderings of similarity measures before and after the rectifications respectively

4.2 局部匹配性能实验

由于采用了FFT快速算法,上述整幅图像的匹配时间在Matlab平台上仅需要0.7s,否则匹配时间则需要十几到几十min.对于局部匹配,由于图像之间存在大量的相似结构,匹配窗口过小时,非匹配位置也可能出现较大的测度值,给匹配搜索带来困难.实验采用不同大小的局部匹配窗口,比较FFT梯度相关与互信息方法[5]的匹配性能.为了减少实验计算量,将匹配搜索的范围限定在理想匹配位置周围50像素的移动范围内(事实上采用FFT算法时,搜索范围对计算量没有任何影响,完全可以对整幅图像穷尽搜索).

如图8所示,窗口大小为60×60时,采用互信息测度无法找到正确的匹配位置,而梯度相关的匹配峰值虽然也不太明显,但匹配位置的测度值仍然是全局最大值,是能够确定的.

如图9所示,当窗口大小增加到90×90时,两种匹配测度都是有效的,显然梯度相关测度的显著性更好.

图8 窗口60×60,互信息与梯度相关的匹配测度值Fig.8 Similarity measures of MI and gradient correlation respectively with 60×60 window size

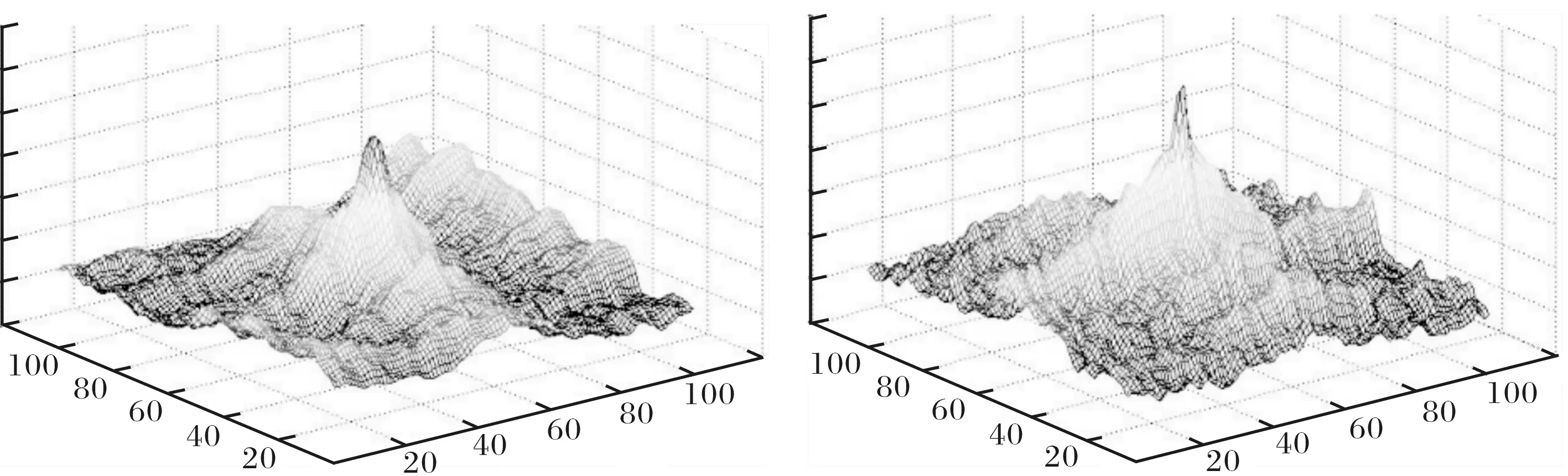
图9 窗口90×90,互信息与梯度相关的匹配测度值Fig.9 Similarity measures of MI and gradient correlation respectively with 60×60 window Size

表1列出了采用互信息方法以及本文提出的梯度相关和FFT梯度相关算法的局部匹配耗时情况,显然本文算法的计算效率有明显的优势.

表1 不同方法的局部匹配耗时

5 结论与展望

将实数域灰度图像转换为复数域的梯度图像,以复数平方运算实现的2倍角余弦作为多模态图像匹配测度的无偏估计,由灰度相关频域快速算法发展到多模态图像的梯度相关频域快速算法.实验证明本文提出的FFT梯度相关算法在精度、速度和可靠性等方面较传统方法都有显著提升.下一步可能研究的方向是梯度场的稳健估计和子像素级精度多模态图像匹配的快速算法.

[1]MIKOLAJCAYKK,SCHMIDC.Aperformanceevaluationoflocaldescriptors[J].PatternAnalysisandMachineIntelligence,IEEETransactionson, 2005, 27(10):1615-1630.

[2]SHAPIROLS,MICHAELBJ.Feature-basedcorrespondence:aneigenvectorapproach[J].ImageandVisionComputing, 1992, 10(5):283-288.

[3]MYRONENKOA,SONGX.Pointsetregistration:Coherentpointdrift[J].PatternAnalysisandMachineIntelligence,IEEETransactionson, 2010, 32(12):2262-2275.

[4]KELMANA,SOFKAM,STEWARTCV.Keypointdescriptorsformatchingacrossmultipleimagemodalitiesandnon-linearintensityvariations[C]//ComputerVisionandPatternRecognition,IEEEConferenceon, 2007:1-7.

[5]MAESF.Multimodalityimageregistrationbymaximizationofmutualinformation[J].MedicalImaging,IEEETransactionson, 1997, 16(2):187-198.

[6]HABERE,MODERSITZKIJ.Intensitygradientbasedregistrationandfusionofmulti-modalimages[J].MethodsofInformationinMedicine, 2007, 46(3):292-299.

[7]HEINRICHMP.MIND:Modalityindependentneighbourhooddescriptorformulti-modaldeformableregistration[J].MedicalImageAnalysis, 2012, 16(7):1423-1435.

[8] 闫 利. 胡修兵,陈长军,等.多模态图像配准的梯度一致性算子[J]. 武汉大学学报(信息科学版), 2013, 38(8):969-972.

[9]WONGA,BISHOPW,ORCHARDJ.Efficientmulti-modalleast-squaresalignmentofmedicalimagesusingquasi-orientationmaps[C].IPCV, 2006:74-86.

[10]REDDYBS,CHATTERJIBN.AnFFT-basedtechniquefortranslation,rotation,andscale-invariantimageregistration[J].ImageProcessing,IEEETransactionson, 1996, 5(8):1266-1271.

[11] 张剑清, 潘 励, 王树根. 摄影测量学[M]. 武汉:武汉大学出版社,2009.

An FFT gradient correlation algorithm for multimodal image matching

XIAN Yanxia1, HU Xiubing2, ZHENG Li2

(1.School of Science, Wuhan University of Science and Technology, Wuhan 430081;2.School of Geodesy and Geomatics, Wuhan University, Wuhan 430079)

Multimodal image matching is a hot and difficult issue in various image matching research fields. The reproducible detection of features and nonlinear optimization are bottlenecks of the feature-based and area-based image matching methods, respectively. The images are converted from grayscale to gradient domain in complex field, and the similarity measure of Double-angled cosine is desinged base on the squared gradient orientation image. Thus, the FFT gradient correlation algorithm is proposed to match multimodal images rapidly.

multimodal image matching; gradient correlation; FFT; conjugate complex; infrared image

2015-03-20.

国家自然科学基金项目(41001309).

1000-1190(2015)06-0838-05

TP391.41

A

*E-mail: whu2014@qq.com.