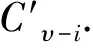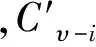有限链环上线性码和循环码的结构
2015-03-21石立叶邱双月刘丽英
石立叶, 邱双月, 刘丽英
(邯郸学院 数理学院, 河北 邯郸 056005)
石立叶*, 邱双月, 刘丽英
(邯郸学院 数理学院, 河北 邯郸 056005)
设R是有限链环,R上长度为n的线性码C等同于模Rn的子模,循环码等同于R[x]/(xn-1)的理想.定义C[γi]={x|x∈C,γix=0},那么C[γi]是Rn的子模,且C[γi]/C[γi-1]是自由模.进一步当C是循环码时,C[γi]/C[γi-1]同构于K[x]/(xn-1)的某个理想.由此出发,给出了有限链环上线性码的结构和循环码的结构,证明并拓广了Norton的有关结论.
有限链环; 线性码; 循环码
1994年,Kumar等人在文献[1]中指出,一些重要的二进制非线性码,如Preparata码,Kedock码,Goethals-Delsarte码等可以看做环Z4上的线性码在Gray映射下对应的像.因此,环上码的研究成为编码理论工作者研究的一个热点.环Z4上的线性码和循环码已被广泛研究并得到了丰富的结果[2-6].Galderbank和Sloane给出了Zpk环上循环码的结构[5].Blackford 和 Ray-Chaudhuri在文献[6]将这一结果推广到Galois环上.Norton和Salagean给出了有限链环上线性码和循环码的结构[7].Douyherty和刘宏伟应用幂等元研究有限链环的理想,从而得到有限链环上的循环码的构造[8].本文进一步研究了有限链环上的线性码和循环码的性质,并给出了它们的结构.
1 有限链环上的线性码
定义1[1]一个含单位元1的有限交换环称为有限链环,如果1≠0并且它的全部理想能按照包含关系排成一条链.
通过定义发现有限链环R的所有理想都是主理想,因为若R的理想I不是主理想,则I至少有两个生成元,不妨设I=〈a1,a2,…,as〉,则〈a1〉⊄〈a2〉,〈a2〉⊄〈a1〉,与R是有限链环矛盾.这也表示,有限链环极大理想是唯一的.
设R是有限链环,Γ是其极大理想,则Γ是主理想.设γ为Γ的生成元,即Γ=〈γ〉.那么,可得下链
R=〈γ0〉⊇〈γ1〉⊇…⊇〈γi〉⊇…
因为R有限,上链不会无限不终止,即存在自然数i,使得〈γi〉=0.设υ是使得〈γυ〉=0的最小的自然数,那么υ就叫做γ的幂零指数.
由上面叙述可以得到有限链环的极大理想的3个重要性质:首先,γ是幂零的,设其幂零指数为υ,则R的所有理想为γiR=〈γi〉,0≤i≤υ,且满足链R=〈γ0〉⊇〈γ1〉⊇…⊇〈γυ〉=0;此外,极大理想Γ中所有元都是零因子,并且包含了环R的全部零因子;最后,集合RγR中任何元素是单位,R/γR是有限域,不妨设为K.因此,有限链环R存在如下唯一分解:
引理1[7]任意r∈R{0},存在唯一整数i,0≤i≤υ,使得r=uγi,其中u是单位,且u在modγυ-i下是唯一的.
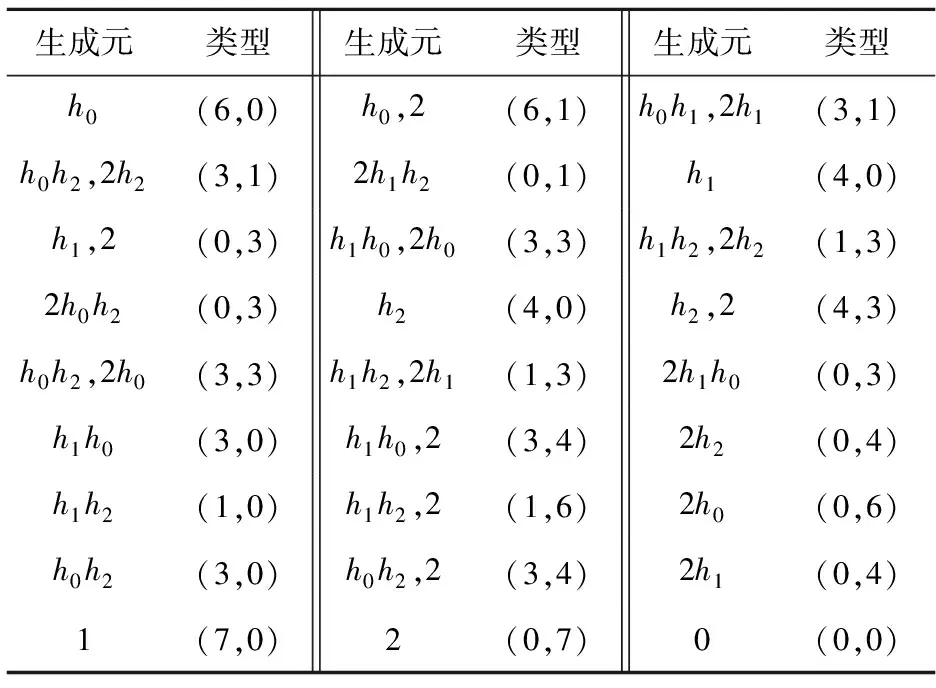
引理2[7]若1≤i 引理3 任取x∈R,若γmx=0,γm-1x≠0,那么Rx≅R/γmR≅γυ-mR. 证明做映射φ:R→Rx,φ(r)=rx.下证Kerφ=γmR.显然γmR⊆Kerφ;任取y∈Kerφ,即yx=0.设y=γαy1,y1是单位,则yx=γαy1x=0,得γαx=0,故α≥m,即y∈γmR.得证. 符号同上,考虑有限链环R上的线性码C.因为有限链环R上一个长度为n的线性码C是R-模Rn的一个子模,反之也成立,所以,只要研究Rn的子模即可. 设M是Rn的一个R-子模,定义M[γi]={x|x∈M,且γix=0}.易证M[γi]是Rn的子模,且满足下链 M=M[γυ]⊇M[γυ-1]⊇…⊇M[γ0]=0. M[γi]/M[γi-1]是R/γR-模,即K-模.因为主理想环上无扭的有限生成模一定是自由模,又K是域,且M[γi]/M[γi-1]是无扭模,所以,M[γi]/M[γi-1]是自由模,也可看做数域K上的线性空间.设其秩或其维数为tυ-i,1≤i≤υ,令k0=t0,ki=ti-ti-1,1≤i≤υ-1. 为了书写方便,记Mi=M[γi]/M[γi-1].那么,Mi具有如下性质: 定理1符号同上,则 (1)Mi中的元都可表示为γυ-iu的形式,其中u是单位或0; (2)Mi≅(γυ-iR)tυ-i; (3)ti≤ti+1,即ki≥0. 证明(1)任取a∈Mi,若a=0,取u=0.若a≠0,由引理1,a=uγj,0≤j≤υ,其中u是单位.又由Mi的定义知,γia=0,γi-1a≠0,故γi+ju=0,γi+j-1u≠0,所以.j=υ-i. (2)若Mi=Mi-1,命题显然成立. 若Mi≠Mi-1,因为Mi是自由模,且秩为tυ-i,不妨设u1,u2,…utυ-i是一组基,即Mi≅Ru1⨁Ru2⨁…⨁Rutυ-i.又γiuj=0,γi-1uj≠0,0≤j≤tυ-i.应用引理3,Ruj≅R/γiR≅γυ-iR,命题得证. (3)γMi⊆Mi-1,所以,Mi的一组基的γ倍是Mi-1基的一部分.所以, dimMi≤dimMi-1,即tυ-i≤tυ-i+1,所以,ki≥0,0≤i≤υ. 以此类推,最终得到M[γ]的基为: 推论1dimMi=tυ-i=k0+k1+…+kυ-i. 这就意味着码C中所有码字可表示为(v0v1…vυ-i)G,其中每个向量vi的长度为ki,向量中的元都属于γiR.由此,给出码的类型的定义. 定义2[9]向量(k0,k1,…,kυ-1)叫做码C的类型,ki叫做维数. 由前面讨论,那么对于有限链环Zpα上的非零的类型为(k0,k1,…,kυ-1)的线性码C来说,C所包含的码字个数为1k0pk1(p2)k2…(pυ-1)kυ-1. 定义3[9]有限链环R上线性码C的对偶码定义为C⊥={ω∈Rn|(u,ω)=0,∀u∈C},其中(u,ω)表示通常的内积. 关于对偶码的类型有如下结论: 定理3[9]设C是R上类型为(k0,k1,…,kυ-1)的线性码,则C⊥的类型为(kυ,kυ-1,…,k1),kυ=n-k0-k1-…-kυ-1. R上的线性码C叫做循环码,是指若c=(c0,c1,…,cn-1)∈C,则C的循环移位(cn-1,c0,c1,…,cn-2)∈C. 假设K的特征不能整除n.考虑R上的多项式环R[x]模xn-1的剩余类环R[x]/(xn-1).在同构映射φ:Rn→R[x]/(xn-1),(c0,c1,…,cn-1)|→c0+c1x+…+cn-1xn-1下,环R上的循环码C等同于R[x]/(xn-1)的理想. 和线性码的讨论类似,记Ci=C[γi]/C[γi-1].易证C[γi]是Rn的理想,由环同态定理可知Ci是Rn/C[γi-1]的理想. 任取a+C[γi-1]∈Ci,由定理1和引理1,存在唯一的a1,使得a=γυ-ia1,其中a1是单位或0.因此,定义映射ψ:Ci→K[x]/(xn-1),ψ(a+C[γi-1])=a1.因此a1≡a(modγυ-i),且有下述结论. 引理4上述映射是单同态. 证明任取u=a+C[γi-1],v=b+C[γi-1]∈Ci,设ψ(u)=a1,ψ(v)=b1. 由同余性质u≡a1,v≡b1,则u+v≡a1+b1,uv≡a1b1,可得ψ(u+v)=ψ(u)+ψ(v),ψ(uv)=ψ(u)ψ(v).即ψ是同态. 设u≠v.若ψ(u)=ψ(v),即a1≡b1(modγυ-i),那么a≡b(modC[γi-1]),与u≠υ矛盾. 综上,ψ是单同态. 由引理4可以看出,Ci和K[x]/(xn-1)的某个理想同构,所以,可以根据有限域上循环码的结构来推导有限链环R上循环码的结构. 引理5有限域K上的一 个[n,k]循环码C具有生成多项式g(x),degg(x)=n-k.若g(x)首1,则g(x)是唯一的. 定理4Ci可以看做有限域K上的循环码,且Ci是[n,tυ-i]循环码,即Ci具有生成多项式γυ-igυ-i(x),γ|/gυ-i(x).且deggυ-i(x)=n-tυ-i.若gυ-i(x)首1,则gυ-i(x)是唯一的. 由Ci中元的性质以及映射ψ的定义知fυ-i(x)=γυ-igυ-i(x),γ|/gυ-i(x),且Ci=γυ-igυ-i(x). 定理5设(p,n)=1,C是R上长为n的循环码,则存在多项式g0(x),g1(x),…,gυ-1(x),使得C=〈g0(x),γg1(x),…,γυ-1gυ-1(x)〉.且gυ-1(x)|gυ-2(x)|…|g0(x)|xn-1.若gi(x)是首1的,则这些多项式是唯一的. 证明由定理2的证明过程并结合定理4可得C=〈g0(x),γg1(x),…,γυ-1gυ-1(x)〉,且若gi(x)首1,则gi(x)是唯一的. 又γCi⊆Ci-1,即γυ-i+1gυ-i+1(x)|γ(γυ-igυ-i(x)),得gυ-i+1(x)|gυ-i(x).证毕. 定理5虽然给出有限链环上的循环码的生成多项式的特点,但是怎样利用xn-1的分解式去构造一个具体的、或是给定类型的循环码还不行,需引入以下的概念和结论. 定义4[9]一个多项式f称为无平方因子,若g2|f,则g只能是单位. 引理6[9]若(p,n)=1,那么xn-1在K[x]上无平方因子.也就是说xn-1在K[x]上可分解成两两互素的不可约多项式之积. 结合定理5得到下面结论. 定理6设(p,n)=1,C是R上长为n的循环码,且码的类型为(k0,k1,…,kυ-1),则存在唯一的首项系数为1且两两互素的多项式f0(x),f1(x),…,fυ-1(x),使得gi(x)=fi(x)fi+1(x)…fυ-1(x),0≤i≤υ-1. 证明符号同上,存在唯一的首项系数为1的多项式g0(x),g1(x),…,gυ-1(x),使得C=〈g0(x),γg1(x),…,γυ-1gυ-1(x)〉,deggυ-i(x)=n-tυ-i. 由前面符号记法k0=t0,ki=ti-ti-1,1≤i≤υ-1.得tυ-i=k0+k1+…+kυ-i,所以deggi(x)=n-ti=n-(k0+k1+…+ki)=ki+1+ki+2+…+kυ.定义fυ-1(x)=gυ-1(x),fi=gi/gi+1,0≤i≤υ-2,所以, degfi(x)=ki+1. 下证f0(x),f1(x),…,fυ-1(x)两两互素. 若fi(x)与fj(x)不互素i≠j.不妨假设i 定理5和定理6给出了构造有限链环上非零循环码的具体方法: 首先将xn-1分解成两两互素的不可约多项式的乘积,不妨设xn-1=h0(x)h1(x)…ht(x),其中h0(x),h1(x),…,ht(x)两两互素; 其次,构造多项式f0(x),f1(x),…,fυ-1(x),其中fi(x)是上述不可约多项式,再加上常数1所构成的新的多项式集合中的部分多项式的乘积,且fi(x)两两互素.这里degfi(x)=ki+1; 最后,依次作多项式gυ-1(x),gυ-2(x),…,g0(x),其中gi(x)=fi(x)fi+1(x)…fυ-1(x),则C=〈g0(x),γg1(x),…,γυ-1gυ-1(x)〉.C的类型是(k0,k1,…,kυ-1). 上述方法在具体操作过程还需要考虑一些细节问题.由循环码的构造方法易得下面定理7. 定理7[11]R上长度为n的循环码的个数为(υ+1)r,r是xn-1的分解式中不可约因子的个数. 例1考虑整数剩余类环Z4上长度为7的循环码.Z4的极大理想是〈[2]〉,[2]的幂零指数υ=2.在F2上x7-1=(x-1)(x3+x+1)(x3+x2+1)=h0(x)h1(x)h2(x),即r=3,所以共有27个循环码. 可以这样去构造一个循环码: 选取f0=h0,f1=h1,由于degfi(x)=ki+1,那么k1=1,k2=3,所以k0=7-1-3=3,即C是一个类型为(3,1)循环码,生成元是γf1,f1f0. 通过上述方法,可以够造出Z4上长度为7的所有循环码. 表1 环Z4上长度为7的循环码 [1]HammonsAR,KumarPV,CalderbankAR,etal.TheZ4linearity of kerdock,preparata,goethals,and related codes[J].IEEE Trans Inform Theory, 1994, 40(2):301-309. [2] Pless V,Sole P,Qian Z.Cyclic self-dualZ4-codes[J].Finite Fields Appl, 1997, 3:48-69. [3] Calderbank A R,Mc G G,Kumar P V,et al.Cyclic codes overZ4,locator polynomials and Newton's identities[J].IEEE Trans Inform Theory, 1996, 42(1):217-226. [4] Kanwar P,Lopez-Permouth S R.Cyclic codes over the integers modulopm[J].Finite Fields Appl, 1997, 3:334-352. [5] Calderbank A R,Sloans N J A.Modular andp-adic cyclic codes[J].Designs,Codes and Cryptography, 1995, 6:21-35. [6] Blackford J T,Ray-Chaudhuri D K.A transform approach to permutation groups of cyclic codes over Galois rings[J].IEEE Trans Inform Theory, 2000, 46(7):2350-2358. [7] Norton G H, Salagean A.On the structure of linear and cyclic codes over a finite chain rings[J].Applicable Algebra in Engineering,Communication and Computing, 2000, 10:489-506. [8] Dougherty S T, Liu H W. Cyclic codes over formal power series rings[J]. Acta Mathematica Scientia (English Version), 2011, B31(1):331-343. [9] Norton G H, Salagean A. On the structure of linear and cyclic codes over a finite chain ring [J].Appl Algebra Eng Comm Comput, 2000, 10:489-506. [10] Norton G H, Salagean A. On the Hamming distance of linear codes over a finite chain ring [J].IEEE Trans Inform Theory, 2000, 46(3):1060-1067. [11] 李光松,韩文报.有限链环上的循环码及其Mattson-Solomn多项式[J].高校应用数学学报(A辑), 2004, 19(2):127-133. The structure of linear codes and cyclic codes over finite chain rings SHI Liye, QIU Shuangyue, LIU Liying (Department of Mathematics and Physics, Handan College, Handan, Hebei 056005) LetRbeafinitechainring,alinearcodeoflengthnoverRisanR-submoduleofRn, and a cyclic code of lengthnisanidealofR[x]/(xn-1).LetC[γi]={x|x∈C,γix=0},thenitisasubmoduleofRn,andC[γi]/C[γi-1]isafreemodule.Moreover,ifCisacycliccode,thenC[γi]/C[γi-1]isisomorphicwithanidealofK[x]/(xn-1).Startingfromthis,thestructureoflinearcodesandcycliccodesoverfinitechainringswerestudiedinthispaper.Also,someNorton’smainresultswereshowninadifferentwayandwereextended. finite chain ring; linear code; cyclic code 2014-09-22. 河北省教育科学研究“十二五”规划课题(1406028). 1000-1190(2015)03-0348-04 O157.4 A *E-mail: sxxshily@163.com.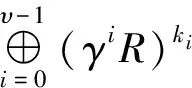
2 有限链环上的循环码