一种高频雷达回波谱反演海浪的新算法❋

常广弘, 黎 明❋❋, 楚晓亮, , 纪永刚, 于长军

(1.中国海洋大学, 山东 青岛 266100；2.国家海洋局第一海洋研究所, 山东 青岛 266061；3.哈尔滨工业大学(威海), 山东 威海 264209)



一种高频雷达回波谱反演海浪的新算法❋

常广弘1, 黎 明1❋❋, 楚晓亮1, 2, 纪永刚2, 于长军3

(1.中国海洋大学, 山东 青岛 266100；2.国家海洋局第一海洋研究所, 山东 青岛 266061；3.哈尔滨工业大学(威海), 山东 威海 264209)

在高频地波雷达海浪谱反演问题中, 广泛采用的Barrick后向散射公式属于第一类非线性Fredholm积分方程。此类积分方程的解在本质上是不适定的，加之高频雷达二阶回波信号信噪比较低，使得反演海浪谱存在解不稳定的问题。本文提出一种稳定且低复杂度的反演算法，此算法首先根据高频雷达一阶回波谱测量海浪方向，并将其引入积分方程求解过程，减少求解变量的个数，降低反演算法的复杂度。为解决反演结果不稳定的问题，使用Tikhonov正则化方法并利用广义交叉验证法(GCV)确定其正则化系数。通过在不同测试条件下对反演算法的仿真测试分析，表明此方法具有运算量小、稳定性好的特点。

高频地波雷达； 海浪谱； 反演； 正则化

高频地波雷达发射垂直极化电磁波(3～30MHz)绕海面传播的过程中与海浪相互作用产生后向散射，雷达回波谱中包含丰富的海表面状况信息。Hasselmann[1]提出了二阶水动力和电磁作用产生二阶峰的概念，认为一阶峰周围的二阶峰正比于海浪频谱。在此基础上，Barrick[2-3]根据电磁波的微扰展开原理，并假设海表面为良导体，推导了后向散射公式，此公式属于第一类非线性Fredholm积分方程。

基于Barrick后向散射公式，Barrick[4]、Lipa[5]、Wyatt[6]、Gurgel[7]和Howell[8]等人都提出了通过雷达回波谱提取海浪信息的算法。其中，Barrick法对二阶峰的积分进行处理，可测量有效波高；Lipa将回波谱分段处理，分别得到方向分布系数和长浪区域的海浪谱；Gurgel采用计算回归系数的方法反演海浪有效波高；Howell将海浪谱展开成有限项傅里叶级数的形式，该方法存在截断误差。吴雄斌等[9]修正了Barrick反演模型，提高了模型抑制噪声和抗干扰的能力，并且使模型应用于宽波束雷达，通过与浮标测量结果对比，证明了有效波高测量的有效性。

Lipa和Howell的海浪谱反演算法属于对第一类非线性Fredholm积分方程的求解，此类方程的解在本质上是不适定的[10](不适定问题的概念为：解存在、解唯一和解稳定[11])，而且高频雷达二阶回波信号信噪比较低，加剧了反演结果的不稳定性，因此，采用适当的正则化方法是非常必要的。李伦等[12]对积分方程离散化处理后，采用正则化方法，得到方程的正则逼近解，通过仿真实验证明了算法的有效性，但此种方法需要对大型矩阵进行操作，运算量较大。

本文提出的反演算法使用雷达一阶回波来测量海浪方向，并将其引入积分方程求解过程，减少了反演中求解变量的个数，为保证反演结果的稳定性，使用Tikhonov正则化方法并利用广义交叉验证法(GCV)确定其正则化系数。本文在详细介绍反演算法的基础上，通过不同条件下的仿真测试，分析了算法的特点。

1 反演算法

本节首先介绍Barrick后向散射公式，在此基础上，使用两种策略来降低反演算法的复杂度：第一，引入海浪方向信息，减小反演过程中未知变量个数；第二，对离散化处理后的海浪谱进行近似处理，降低反演过程中的矩阵维数。

1.1 后向散射公式

无海流情况下的一阶后向散射公式为[1]：

(1)

其中:m′=±1表示多普勒频移的正负；k0为雷达电磁波波矢，以发射电磁波方向为正,k0为其波数；S(·)为海浪方向谱；δ(·)为狄拉克函数；波数为雷达电磁波波数2倍的海浪产生最强的后向散射，并根据深水行进波色散关系ωB与k0之间满足：

(2)

其中:g为重力加速度。

无海流情况下的二阶后向散射公式为[3]:

(3)

其中：m,m′=±1表示产生后向散射的4种海浪组合；k和k′为产生后向散射的两列海浪波矢；k和k′分别表示两列海浪的波数;Γ为耦合系数[5]。

1.2 反演算法

对式(3)进行归一化处理并根据狄拉克函数的性质进行化简：

(4)

其中:η=ω/ωB为归一化多普勒角频率;K=k/(2k0)、K′=k′/(2k0)为归一化的海浪波数，为消除雷达增益及路径损失等对回波的影响，将二阶峰除以一阶峰能量，得到归一化的二阶谱：

(5)

为了降低算法的复杂度，减少反演参数，将海浪方向谱表示为海浪谱与方向分布因子乘积的形式：

S(k)=S(k)·G(θw)

(6)

海浪方向可以通过正负一阶峰的幅值差[14]来求得:

|θw|=2tan-1(10R/(10s))

(7)

其中:R=10log(B+/B-)，B+与B-分别为正负一阶峰的幅值。

根据狄拉克函数及海浪的特性，将(6)带入(5)，并引入S(k′)进行线性化处理，在反演过程中，为了避免过多的引入误差，只对能量最强的二阶峰进行操作，在此以m=m′=1为例进行介绍：

(8)

σ=Kn×S

(9)

i=1,2…n,

其中：σ∈Rn×1为已知的归一化二阶回波谱频点；Kn∈Rn×(n·m)为系数矩阵，S∈R(n·m)×1为海浪谱。由于方程数量要远小于未知数个数，且离散后的海浪谱中含有大量的重复及近似元素。因此，对离散后的S矩阵进行排序，隔m点取值作为S的近似值，将S矩阵进行降维，并将核矩阵Kn中对应于相同S的元素求和得到C矩阵。于是式(9)可表示为：

σ=C×S

(10)

其中：C∈Rn×n为系数矩阵；S∈Rn×1为海浪谱，通过求解此方程组便可以得到海浪谱S。

2 正则化方法及算法流程

实际处理中，式(10)中系数矩阵C存在不满秩的情况，此时C的逆不存在，而基于广义逆方法求得的海浪谱S使残差‖CS-σ‖2取最小值，即S=C+×σ，但此解的稳定性得不到保证，因此采用适当的正则化方法是必要的。正则化方法可以分为两类：Tikhonov正则化方法和Landweber迭代方法。当矩阵维数较小时，Tikhonov方法运算量要小于Landweber迭代算法。由于已经对矩阵进行了降维处理，选择Tikhonov正则化方法，来降低整个算法的运算量。此方法中涉及正则化系数的选择问题，为了得到最优的正则化系数，引入GCV正则化系数选择方法。

在此，根据Tikhonov正则化方法原理及所求海浪谱S为有界且光滑的特性，在解中增加罚项，若解的最初估计为S*，则增加的罚项为：

Ω(S)=‖S-S*‖2

(11)

增加罚项后必须考虑‖CS-σ‖2与Ω(S)之间的关系，Tikhonov通过引入正则化系数[15-16]来权衡两者的大小，即

(12)

其中：λ为正则化系数，控制残差范数及罚项Ω(S)使得解范数最小化，将求解不适定问题转化为最优化参数选择的问题。很明显，当λ较大时，可使海浪谱比较平滑，但会丢失海浪谱的细节信息；当λ较小时，所求得的海浪谱使得残差较小，但海浪谱受雷达回波谱中噪声的影响较大。因此，正则化系数的选择是一个非常关键的问题。

计算正则化系数一般有L曲线法和GCV法，在处理离散问题时，L曲线法要进行曲线拟合和插值处理，导致计算量增大。在此采用GCV法[17]，此方法的计算公式可以表示为：

(13)

其中：Cλ为正则化矩阵；tr表示矩阵的迹。GCV法通过改变λ的值，使得GCV(λ)取得最小值，来求取最优化的正则化系数，即得到最终适定的正则化解：

Sλ=Cλσ

(14)

经过离散化处理与正则化处理后，最终得到了后向散射方程的正则逼近解Sλ，算法流程见图1。

3 仿真验证及分析

设计4组仿真实验来验证本文算法的正确性。实验的基本思路是首先利用式(1)和(3)，将雷达频率、风向、风速和信噪比作为输入变量，计算雷达回波谱[18]，然后通过改变不同输入来检验反演算法的效果。仿真中采用Pierson-Moskowitz 海浪谱与Longuet-Higgins方向分布函数之积来表示海浪方向谱，公式如下：

(15)

其中:α=8.1×10-3;β=0.74;kc=g/U2，U为海平面上方19.5m处的风速;s为方向分布系数;θw为风向与参考方向之间的夹角。仿真中使用的海浪谱与海浪频谱之间存在如下关系：

(16)

通过海浪方向谱可以计算海浪的有效波高[7]：

(17)

其中:f为海浪频率;θ为海浪方向。

实验一为信噪比实验，雷达频率为25MHz，风向与雷达法线方向的夹角θw=135°，风速U为14m/s，为了验证算法的稳定性，在仿真产生的回波谱中增加加性高斯白噪声，公式如下：

(18)

其中:σt为仿真产生回波谱;P(σt)为σt能量强度;SNR为信噪比;er为服从标准正态分布的随机数序列。

图2中黑线为仿真产生的雷达回波谱，红色为回波谱中增加噪声的结果，当信噪比为30dB时，雷达回波谱中左侧的二阶峰几乎被噪声淹没，在此情况下只能选择能量较强的二阶峰来进行计算。图3为对应图2中雷达回波谱计算出的反演结果，其中黑线为仿真产生的P-M海浪谱，红线为反演结果，随着信噪比的降低，反演结果的扰动逐渐增大，使得海浪谱中各频率分量与真值相比产生的偏差逐渐增大，但整个海浪谱能量的分布及主波频率仍较清晰。

图1 海浪反演算法流程图Fig.1 The algorithm flowchart of ocean wave inverse

实验二为风向实验，雷达频率为25MHz，风速U为14m/s，风向与雷达法线方向的夹角θw依次为90°和135°，为了防止噪声将较弱的二阶峰淹没，回波谱仿真的信噪比设置为30dB，同时，为了验证算法对低信噪比的反演精度，反演中使用的雷达回波信噪比设置为15dB。

图4中a图为仿真产生的雷达回波数据，其中黑线对应的风向θw为90°的情况，红线对应风向θw为135°的情况。b和c图采用本文算法计算得到的海浪谱数据，由于算法中首先测量出海浪方向，因此，风向的变化对海浪谱的反演产生的影响较小。

实验三为海况实验，雷达频率为25MHz，风向与雷达法线方向的夹角θw为135°，信噪比为雷达法线方向的夹角θw为135°，信噪比为15dB，风速U为依次为8、14和20m/s。

图5中，当海况较低时，雷达回波谱中二阶峰的幅值较低，受到噪声的影响较大，使得反演出的结果有较明显的抖动，但海浪谱中各频率能量的分布趋势仍较为明显；随着海况的增加，噪声对反演结果的影响会相对减小，由于本文算法基于Barrick后向散射公式，此公式又基于电磁波的微扰展开原理，因此，反演波高的范围存在限制k0h<4[19]，其中k0为电磁波波数，h为均方根波高。

图2 不同信噪比下的仿真回波谱Fig.2 Simulated radar spectra with different SNR

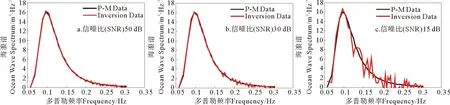
图3 不同信噪比下的反演海浪谱

图4 不同风向下仿真及反演结果

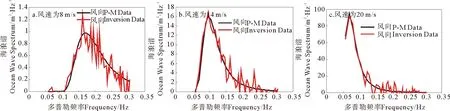
图5 不同海况下反演海浪谱

实验四为雷达频率实验，风向与雷达法线方向的夹角θw为135°，信噪比为15dB，风速U为8m/s，雷达频率分别为13、18和25MHz。

图6中，黑线为海浪谱真值，红线为反演结果，为观察不同频率雷达所能反演海浪谱的频率范围，真值海浪谱只显示反演频带内的幅值。在反演过程中要进行线性化处理，因此二阶峰的选择区域是有限制的，一般选择的区域为1.1～1.4fB[8]，同时对海况的高低也是有限制的,较低的雷达频率将不能测量低海况[20]。当雷达频率降低时，反演海浪谱的频率上限会逐渐降低，使反演海浪谱的频率范围存在截断现象。

表1为4组实验测量的有效波高误差结果，使用本算法反演海浪谱信噪比在高于15dB时是比较可靠的，例如，雷达频率为25MHz时，有效波高的相对误差为8.03%。在实际系统中可以剔除信噪比低于15dB的数据，来增加反演海浪的精度。

图6 不同雷达频率下反演海浪谱

实验一Experiment1实验二Experiment2实验三Experiment3实验四Experiment450dB30dB15dB90°135°8m·s-114m·s-120m·s-113MHz18MHz25MHz有效波高①/m4.184.184.184.184.181.364.188.541.361.361.36绝对误差②/m0.030.030.020.030.040.110.020.000.370.220.11相对误差③/%0.640.600.470.730.988.350.400.0427.1116.228.03均方根误差④/m0.100.110.220.290.240.450.210.561.430.860.43

Note:①Signifigent wave high; ②Absolute error; ③Relative error; ④Root-Mean-Square error

在低海况及低频段的反演中，海浪谱的反演结果出现较大的扰动现象，主要是由两方面原因造成的：第一，较低的海况激起的二阶峰幅值太小，反演的结果受噪声的影响大，表现为海浪谱的抖动；第二，在海浪谱的高频段区域，由于雷达截面方程中等频线未能完全覆盖，导致反演时信息量小，产生抖动现象[12]。对于第一个原因，可以通过增加雷达频率来解决；对于第二个原因，可以使用模型或f-5衰减因子来近似拟合海浪谱的抖动及截断部分。

4 实验验证初步结果

为进一步验证算法的有效性，将反演算法应用于实测数据，雷达频率为13.021MHz。图7为实测某波束的距离-多普勒回波谱，其中横坐标为频率，纵坐标为距离单元，正负一阶峰均向右产生偏移，此偏移由海流产生，正一阶峰右侧存在明显的二阶峰，虽然受海流的影响产生了严重的频偏，但可以直接通过平移整个频谱来移除海流的影响[21]。

雷达回波数据为多普勒频率、距离和波束的三维数据，对于某个波束和距离的雷达回波谱运用反演算法，便可以得到此波束和距离的海浪谱。在此，提取图7中的第9距离单元的回波频谱(见图8)。本算法自动选择一阶峰与二阶峰之间的低谷作为二阶峰范围的起始点，1.4fB作为终止点。

图9为反演得到的海浪谱结果，有效波高为2.25m，与当时国家海洋局预报的有效波高2m吻合，频率范围为0.08～0.24Hz，此频率范围已包含了大部分海浪的能量。

图7 实测距离-多普勒回波谱

图8 雷达多普勒回波谱

图9 反演海浪谱

图10为2013年1月9日下午采集的高频雷达数据采用不同算法得到的有效波高测量结果，时长3.5h，其中黑线为未经过正则化处理结果，红线为采用正则化处理结果。很明显黑线有3处较大的突变，是雷达回波中噪声引起的求逆结果不稳定造成的，而红线更加平滑稳定，符合海浪有效波高的变化规律。

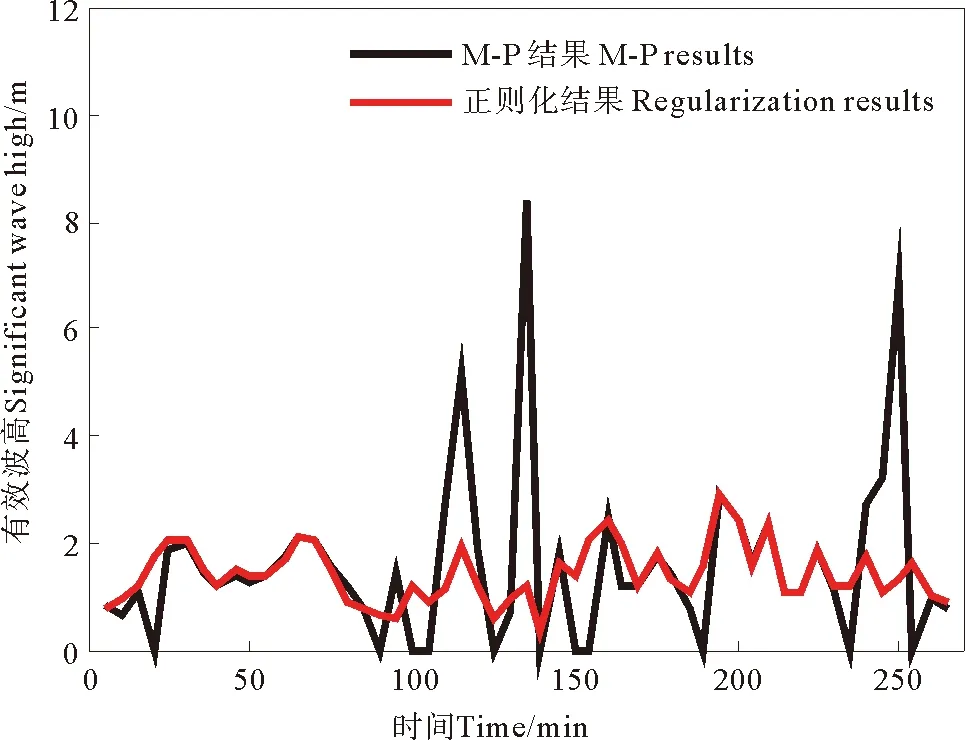
图10 M-P逆与正则化处理实测有效波高结果比较

5 结语

本文提出的一种低复杂度的高频雷达海浪反演算法，通过仿真验证，在信噪比高于15dB时，能较准确的反演海浪谱，并且本算法复杂度较低，反演的结果稳定，如果只用来反演有效波高，则所需的信噪比还可降低。方法中海浪谱的方向分布系数s采用了经验值，在后续工作中可通过回波谱数据计算得到s的具体数值，来提高反演的精度。

[1] Hasselmann K. Determination of ocean wave spectra from Doppler radio return from the sea surface [J]. Nature, 1971, 229:16-17.

[2] Barrick D E. First-order theory and analysis of MF/HF/VHF scatter from the sea [J]. IEEE Trans Antennas Propag， 1972, AP-20: 2-10.

[3] Barrick D E. Remote Sensing of Sea State by Radar [C].// Derr V E. Chapter 12 of Remote Sensing of the Troposphere, NOAA/Environmental Research Laboratories Boulder: 1972: 1-6.

[4] Barrick D E, Weber B L. On the nonlinear theory for gravity waves on the ocean’s surface. Part II: Interpretation and applications [J]. J Phys Oceanogr, 1977, 7: 11-21.

[5] Lipa B J, Barrick D E. Extraction of sea state from HF radar sea echo: Mathematical theory and modeling [J]. Radio Sci, 1986, 21: 81-100.

[6] Wyatt L R. HF radar measurements of the ocean wave directional spectrum [J]. IEEE J Oceanic Eng, 1991, 16: 163-169.

[7] Essen H H, Gurgel K W, Schlick T. Measurement of ocean wave height and direction by means of HF radar: An empirical approach [J]. Dt Hydrogr Z, 1999, 51: 369-383.

[8] Howell R, Walsh J. Measurement of ocean wave spectra using narrow beam HF radar [J]. IEEE J Oceanic Eng, 1993, 18: 296-305.

[9] WU X B, LI L, SHAO Y X, et al. Experimental Determination of Significant Waveheight by OSMAR071: Comparison with Results from Buoy [J]. Wuhan University Journal of Natural Sciences, 2009, 14( 6): 499-504.

[10] Delves L M, Mohamed J L. Computational Method for Integral Equations [M]. Cambridge: Cambridge University Press, 1985: 376.

[11] Hadamard J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations [M]. New Haven: Yale University Press, 1923.

[12] Li L, Wu X B, Long C, et al. Regularization inversion method for extracting ocean wave spectra from HFSWR sea echo [J]. Chinese J Geophys (in Chinese), 2013, 56(1): 219-229.

[13] Moskowitz M. Estimates of the power spectrums of fully developed seas for wind speeds of 20 to 40knots [J]. J Geophys Res, 1964, 69: 5161-5179.

[14] Huang W, Gill E. Extraction of Sea Surface Wind Direction from Bistatic High-Frequency Radar Doppler Spectra [C]. Oceans’11, Hawail： IEEE Conference and Hawaii Exhibition: 2011.

[15] Tikhonov A N， Arsenin V Y. Solution of Ill-Posed problem [M]. Washington D. C: Winston & Sons, 1977.

[16] Tikhonov A N, Goncharsky A V. Ill-Posed Problems in the Natural Sciences [M]. Moscow: MIR Publishers, 1987.

[17] Golub G, Von Matt U. Generalized cross-validation for large-scale problems [J]. Journal of Computational and Graphical Statistics, 1997, 6(1): 1-34.

[18] Lipa B J, Barrick D E. Analysis Methods for Narrow-Beam High Frequency Radar Sea Echo [R]. NOAA Technical Report ERL 420-WPL, 1982, 56.

[19] Wyatt L R. An evaluation of wave parameters measured using a single HF radar system [J]. Can J Remote Sens, 2002, 28( 2): 205-218.

[20] Wyatt L R, Green J J. Measuring high and low waves with HF radar [C]. Bramen： OCEANS 2009- EUROPE, 2009: 1- 5.

[21] Vincent C E. The interaction of wind-generated sea waves with tidal currents [J]. J Phys Oceanogr, 1979, 9: 748-755.

责任编辑 陈呈超

Ocean Wave Inversion Algorithm From HF Radar Echo Spectrum

CHANG Guang-Hong1, LI Ming1, CHU Xiao-Liang1,2, JI Yong-Gang2, YU Chang-Jun3

(1. Ocean University of China, Qingdao 266100, China; 2.The First Institute of Oceanography, SOA, Qingdao 266061, China;3.Harbin Institute of Technology at Weihai, Weihai 264209, China)

In the classification of ocean wave spectrum inversions from HF radar echo, widely used Barrick′s backscatter formula belongs to the nonlinear first kind Fredholm integral equation. However, this kind of integral equation is Ill-posed, moreover, the SNR of HF radar echo is relatively low, the inversion ocean wave spectrum is unstable. In this paper, a stable and low complexity inverse algorithm is presented, which uses the first-order peak to measure the wave direction, and then introduces the direction to the progress of solving the integral function, which deduced the number of variables. In order to solve the instability problem of inversion results, we use Thikhonov Regularization methods, and we use Generalized Cross Validation method to determine the regularization coefficients. Simulation results show that this method is stable and small calculating amount.

High-Frequency Surface Wave Radar (HFSWR); ocean wave spectrum; inversion; regularization

国家自然科学基金重点项目(61032011、61132005)资助

2013-10-13；

2014-05-10

常广弘(1990-)，男，硕士生。E-mail:changguanghong@126.com

❋❋ 通讯作者： E-mail：limingneu@ouc.edu.cn

TN958

A

1672-5174(2015)02-127-07

10.16441/j.cnki.hdxb.20130262