基于朴素贝叶斯的西北太平洋柔鱼渔场预报模型的建立❋

崔雪森， 唐峰华， 张 衡， 伍玉梅, 樊 伟

(中国水产科学研究院东海水产研究所 农业部东海与远洋渔业资源开发利用重点实验室， 上海 200090)



基于朴素贝叶斯的西北太平洋柔鱼渔场预报模型的建立❋

崔雪森， 唐峰华， 张 衡， 伍玉梅❋❋, 樊 伟

(中国水产科学研究院东海水产研究所 农业部东海与远洋渔业资源开发利用重点实验室， 上海 200090)

西北太平洋是中国进行柔鱼(Ommastrephesbartramii)捕捞生产的重要海区，准确预报渔场出现的位置对提高渔业捕捞产量、节省燃油有重要的意义。本研究利用2002—2011年中国在该海域的历史产量数据、渔场时空数据以及包括海表温度、叶绿素浓度a、表温梯度强度和叶绿素梯度强度在内的海洋环境数据，基于朴素贝叶斯方法，建立了西北太平洋柔鱼渔场的预报模型。为满足朴素贝叶斯方法对条件独立性的假设，利用独立成份分析，重新获得相互独立的属性变量。通过求Cohen′s Kappa系数最大值的方法，确定3种CPUE类型的先验概率，建立可用于渔场预报的朴素贝叶斯预报模型。作为实际验证，将2012年7～11月我国柔鱼渔船在西北太平洋实际生产数据与预报的高CPUE渔场位置进行叠加，平均综合预报精度达到69.9%，表明该模型对西北太平洋渔场的预报具有较好效果和可行性。

独立成分分析; 朴素贝叶斯; 渔场预报; 柔鱼

西北太平洋是中国远洋渔船从事大规模商业性捕捞的重要作业海域，柔鱼(Ommastrephesbartramii)是该海域的主要捕捞对象之一。日本在2006—2010年的捕捞产量为0.7～4.2万t，平均2.2万t[1]。中国自1990年代，鱿钓生产规模逐步扩大，近5年来渔船数达200～280艘，年产量在3.6～11.3万t[2]。柔鱼通常分为中部秋生群、东部秋生群、西部冬春生群和中东部冬春生群等4个群体，170°E以西为冬春生群[3-4]，是中国鱿钓船的传统捕捞对象[5]。

和大多数渔场一样，柔鱼渔场的形成和变化也受海洋环境因子的影响。利用鱼类的这一特性，国内外学者对不同鱼类设计了各种渔场分析和预报模型。如陈新军等[6]利用算术平均法(AM)和联乘法(GM)分别建立基于表温因子(表温和表温水平梯度)的综合栖息地指数模型，取得了较好的拟合效果。基于经验累计分布函数(Empirical cumulative distribution function, ECDF)，Zainuddin[7]提供了一种寻找潜在渔场的方法。樊伟等[8]利用广义加性模型(GAM)对柔鱼同SST、叶绿素a浓度、经度和纬度4个变量的关系进行了定量分析，为实现GAM模型的预测的功能奠定了基础。陈雪忠等[9]设计了5(°)×5(°)印度洋长鳍金枪鱼的随机森林模型，也取得了较好的预报效果。

以上研究多综合数个环境因子来分析和预报渔场，使分析结果更加准确，但实际的海洋环境因子之间并非都是独立关系，例如某些海域海表温度与叶绿素a浓度存在着的一定的相关性[10]。而在应用一些模型进行分析时，由于部分因子存在着多重共线性，使分析稳定性大大降低，严重影响了最终的结果[11-12]。如果假设海洋环境因子之间相互独立，也不符合渔场学的实际关系[13]。而且，朴素贝叶斯方法的应用前提条件也是要求输入因子是相互条件独立的。因此，本研究需要先通过独立成分分析的方法从时空和环境变量中提取出相互独立的属性，然后以此作为新的输入变量建立朴素贝叶斯渔场预报模型，从而实现西北太平洋柔鱼西部冬春生群渔场的预报，通过这项工作为提高柔鱼渔业生产效率提供参考。

1 数据来源与处理

本研究中的渔获数据由上海海洋大学鱿钓技术组提供，时间范围为2002—2011年，空间范围为140°E～170°E、34°N～48°N，数据的内容包括日期、经度、纬度、产量、作业次数和平均日产量。时间分辨率为天，经、纬度为实际渔获的位置(由于历史统计的原因，2002年空间分辨率为0．5(°)×0．5(°)。按根据Tian等[14]提供的方法计算CPUE值，即

(1)

其中：∑Catch为1(°)×1(°)网格中一个月的总产量；∑Fishingdays为当月渔船作业的天数之和，CPUE的单位为：t·船-1·d-1。作为模型的输出变量，需要先将CPUE进行离散化处理，即将按CPUE高低划分成若干类别，其中三分位数可将样本在统计基础上分为高、中、低3种级别，这是研究中一种常用的分级方法[15]。同时，由于各个月份CPUE波动范围较大，在全年内取统一的分位点会造成训练数据集中，某些月份高CPUE太少或不存在，不利于各个类别CPUE数量上的平衡。所以根据文献[9]的方法，分别以各个月CPUE的33.3%与66.7%分位点为界，将渔获数据集按CPUE的高低划分为高CPUE、中等CPUE和低CPUE3个级别，以保证各个月份都有三类CPUE渔区的出现。

环境数据包括该海域的海表温度(SST)、叶绿素a浓度(CHL)数据、表温梯度强度(SSTG)数据和叶绿素a浓度梯度(CHLG)数据。前两者均取自http://oceancolor.gsfc.nasa.gov/的月平均数据。为了使环境数据与生产数据匹配，将生产数据和环境数据按1(°)×1(°)的空间分辨率进行网格化处理，并将环境数据点均取在渔区网格的中心点上。

表温梯度强度可应用求温度梯度幅值(Gradient Magnitude,GM)的公式来进行[16]。设当前渔区的上下左右4个网格点的海表温度分别为SSTi±1,j和SSTi,j±1，以差分的格式表示表温梯度为：

SSTGi,j=

(2)

其中：Δy表示i-1行和i+1行之间的距离，单位为km；Δx表示j-1列和j+1列之间的距离，单位为km。

同理，可得到叶绿素a浓度梯度

CHLGi,j=

(3)

最后，以月份和经纬度为关键字，将以上4种环境数据与网格化的CPUE数据进行匹配。

2 渔场预报模型的建立

2.1 预测变量的选择

海表温度、叶绿素a浓度、海表温度梯度和叶绿素a浓度梯度等环境要素对渔场的形成和变化具有很重要的作用[17-19]。同时，柔鱼按着季节进行洄游，但即使在同一季节，西北太平洋柔鱼在不同海区作业渔场最适环境因子也有较大差异[20]。因此，在本研究除了选定海表温度、叶绿素a浓度、表温梯度强度和叶绿素a浓度梯度外，也将月份以及经度、纬度共7个要素作为渔场预报模型中的输入变量，将CPUE作为响应变量。

2.2 模型的建立方法

本研究采用朴素贝叶斯方法建立渔场预报模型，但朴素贝叶斯分类器的条件独立假设在现实情况下很少发生，如果不做处理直接使用，可能导致其分类性能下降[21]。因此，在应用朴素贝叶斯方法进行渔场预报模型训练之前，必须对各个渔场类属性(即渔场时空和环境因子)进行独立成分的分解。

2.2.1 独立成分分析 假设中心化后的渔场时空与环境属性数据用随机向量x=(x1,x2,x3,…,xN)表示,其中N是属性的个数，独立成分量可以定义为向量s=(s1,s2,s3,…,sM)，M是独立成分的个数。独立成分分析的目的是通过线性变换把数据x,转换成独立成分向量,即s=Wx，式中W是非混合矩阵。FastICA算法是实现独立成分分析的一种快速寻优的迭代算法，以负熵最大化作为搜寻方向是其具体算法之一。该算法通过对分离结果的非高斯性度量来表示分离变量之间的相互独立性，当非高斯性度量达到最大时，则表明完成了对各独立分量的分离[22]。

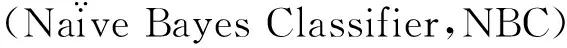
假设X是要输入的随机M维特征变量，记为X=(x1,x2,x3,…,xM)，Y是要输出的目标类别集合，即Y=(C1,C2,C3,…,CK),K是类别数。将训练数据集按不同类别分成K个子数据集，分别利用独立成分分析方法提取出类内相互独立成分s，根据文献[25]的方法，基于对数似然的类条件下朴素贝叶斯分类模型可以表达为：

(4)

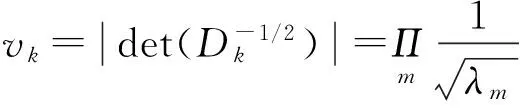
(5)

3 西北太平洋柔鱼渔场预报模型的实现

3.1 渔场时空与环境数据的独立成分分析

2002—2011年西北太平洋柔鱼渔获产量数据与时空及环境数据匹配后，共得到训练数据记录1 223条，以33.3%与66.7%作为各月份CPUE的分位点，将数据集划分为高、中和低CPUE三类，然后利用FastICA方法分别将三类数据集进行独立成分分析。为了避免环境属性信息的损失，仍将独立成份个数定为7，即M=7，最终得到含7个独立成分的记录集和3个相应分离矩阵Wk(k=1,2,3)。

3.2 先验概率的确定

虽然训练数据集的记录按CPUE的分位数进行了三等分，但由于渔船作业范围不能完全覆盖整个研究海域，因此将三类渔场的先验概率组合Pr=(PrH,PrM,PrL)简单地定为(33.3%，33.3%，33.3%)并不一定能获得最高预报精度。Cohen′s Kappa系数可以用作评价判断的一致性程度的指标，也可作为检验该模型精度的一个指标。Kappa系数变动范围在-1～1之间，越大表示2组判断的一致性越高。通用的法则是当Kappa值在0.40～0.75之间时，表明2组判断结果具有一般的一致性[27-28]。所以本研究采用筛选Kappa系数最大值的方法，来获得能使预报与实际渔场分布最大一致性的先验概率值组合Pr。具体方法如下：采用间隔为5%的不同先验概率组合，利用2.2.2节中求得的3类CPUE类别下各个独立成份的边缘密度与特征值，代入公式(4)中，分别得出2002—2011年各月份所有渔区进行分类，分类结果分别与实际生产CPUE分类数据进行比较，求得不同先验概率组合对应的Kappa系数(p值均小于0.001)，将其记为KappaPrH,PrM,PrL。由于PrH+PrM+PrL=100%，因此也可记为

KappaPrH,PrM,PrL=Kappa(PrH,PrL)

(6)

式中：PrH和PrL分别以5%为间隔取5%，10%，15%,…,85%,90%，并且需满足PrH+PrL<100%。以PrH为横轴、PrL为纵轴的获得的Kappa分布等值面(见图1)。由于Pr组合中概率值采样密度间隔为5%，而该图的右上部分PrM<5%，所以只有左下三角区域有实际意义。

从图1中可以看出，当PrH在0.3～0.4之间且PrL在0.2～0.4之间取值时，Kappa值均在0.43左右，即分类的检验结果可达到一般的一致性，其中Kappa(0.35，0.25)=0.444，为最大值。因此，选择(PrH=0.35，PrM=0.40，PrL=0.25)作确定三类CPUE的先验概率值组合。

图1 不同先验概率组合下的Cohen′s Kappa系数

3.3 预报结果与精度检验

经计算得到2012年7～11月的分月高CPUE渔区预报图，并与同期实际生产数据相叠加(其余月份为非渔汛期，缺乏可供验证数据)，如图2所示。

利用公式(5)中的预报精度检验方法，计算得到2012年7～11月的渔场预报准确率如图3所示。从图中可知该年度5个月的预报准确率均在64%～75%之间，平均准确率为69.9%。

4 分析与讨论

4.1 实际精度检验分析

2012年与常年相比渔获生产情况低迷，每月的产量都较上一年明显偏低，渔场范围也比2011年度小，且呈点状分布，这也为预报增加了一定的难度。但全年整体上预报结果和实际生产的渔场重心吻合较好。从定量的预报精度检验结果看，8、9和11月的预报综合准确率均超过了70%，精度比较高，而7和10月为65%左右，相对精度较低。

(a.7月July; b.8月August; c.9月September; d.10月October; e.11月November)图2 2012年实际生产渔场与预报渔场对比图

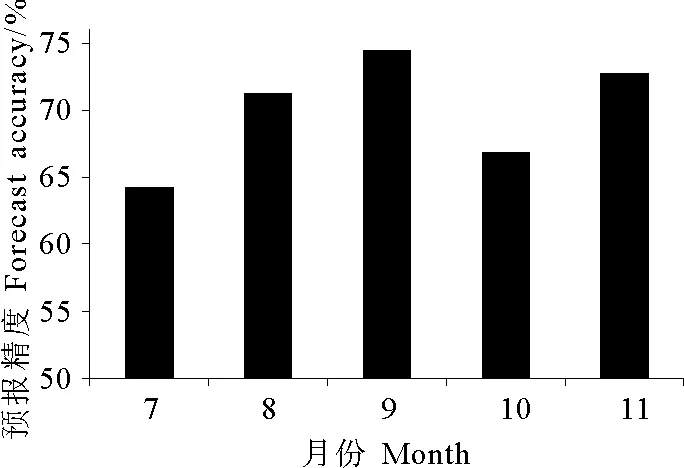
图3 2012年7-11月份渔场预报综合准确率

其中7月份的预报结果较低有2个原因：一是因为虽然在西北太平洋西部海域预报出了高CPUE渔场，但靠近日本的专属经济区附近，没有我国渔船生产，所以缺少实际生产资料进行验证；二是因为7月份在东部(165°E以东)也有渔场存在，但并未做出预报。据资

料记载，2012年7月份165°E以东海域的作业对鱿鱼钓线进行了加长，深度达200～400 m，可能为东部秋生群，而非本研究关注的西部冬春生群，所以造成了7月份预报综合准确率较低。

而10月份精度偏低的原因主要是预报渔区位置普遍偏北所致。根据卫星遥感数据显示，10月份特征等温线(10、15和20 ℃)较常年均偏北，除个别区域外表温偏低外，整个海域的海表温度较常年普遍偏高(见图4)。陈新军认为，柔鱼渔场的在各海区均有一定的适温范围，其中10月份140°E～150°E的适温范围为13～18 ℃，150°E～165°E海域为12～15 ℃[29]。偏高的温度会致使柔鱼的最适温度带整体向北偏移，因此实际渔场与往年相比整体偏北，最终导致使预报准确率降低。这也说明在海洋环境较常年发生较大变动时，利用模型预报渔场后，仍需要结合实际海洋环境对渔场预报位置进行再分析和适当调整。

图4 2012年10月份西北太平洋海表温度与常年对比图

另外，在2012年8和10月的预报结果中，个别海域(如北海道以北145°E、45°N附近)也出现了渔场。据Ichii等的有关研究[30]，西北太平洋柔鱼的冬春生群索饵场的范围并没有包含上述海域，因此这类区域属于预报中的明显误报，应该通过人工干预予以去除。产生这种误报的原因主要是因为模型只考虑了时空及环境要素，而未考虑柔鱼的洄游规律等生物学特征。这也说明了在以环境要素为条件的渔场预报模型中，还需准确掌握目标鱼种生活史过程，才能较大地提高渔情预报精度[13]。

4.2 与其它模型的比较

虽然国内外对于渔场预报模型的探索已有大量研究[6,9,31-32]，但针对西北太平洋柔鱼渔场的中、短期预报的报道却不多见，目前最为普遍使用的是栖息地指数(HSI)模型。Tian等[33]利用HSI模型，结合次表层水温等环境数据获得了2005与2006年的柔鱼冬春生群体渔场预报结果，与实际渔场相比非常吻合，并定量研究了捕捞努力量和CPUE作业次数与平均日产量适宜指数(SI)值与海洋环境的关系；Igarashi等[34]也用相同的模型和包括次表层温度在内的多个海洋环境因子预报了2012年北太平洋东部海域柔鱼秋生群的渔场分布。利用栖息地适应性指数计算得到的预测结果是一个类似于渔场概率的概率值，但作为一个平均化的指标与实时渔场并不具有严格的相关性[13]。

朴素贝叶斯方法有坚实的数学理论基础，通过联合概率来得到一个分类结果，在计算公式中无需计算属性的先验概率，也无需考虑属性之间的相关性，因此具有算法逻辑简单、计算开销小等特点。本研究的实验结果也证明在渔场预报中具有较好的预报精度。与上述HSI模型相比，由于本模型中各个输入环境因子映射到了新的相应独立成分空间，无法直观地对环境因子进行分析，因此还需要借助模型以外的相关性分析等方法对预报结果进行分析和说明，才能获得各个环境因子的重要性指标，这是本模型的不足之处。另外，上述文献中的HSI模型均利用了次表层环境因子作为输入参数，而本模型中只使用了表层的环境信息。一方面次表层更能反映柔鱼所处水层的实际环境，能更准确地把握渔场形成的机理，另一方面，根据现有海洋环境获取设备和条件，大面积、实时地获得次表层环境因子相对表层环境因子更困难，并不适合当前渔场预报业务化运行的应用，因此在本模型的输入参数中未涉及次表层的环境数据。

5 结语

本研究利用独立成份分析的方法，从时空和环境变量中重新提取出条件独立的特征属性，在满足朴素贝叶斯条件独立性假设的情况下，建立了西北太平洋的柔鱼渔场预报模型。由于数据资料的限制，2012年各生产月份的渔获信息仅限于我国鱿钓船的捕捞数据，其他国家和地区的统计数据由于获取困难未能加入其中，这对预报结果的验证和分析带来一定的限制。从整体上看，在选择合适的先验概率的情况下，基于朴素贝叶斯预报模型的预报结果与2012年7～11月我国柔鱼渔船实际生产渔场位置吻合度较好，表明该模型对西北太平洋渔场的预报具有较好效果和可行性。在环境数据方面，由于即时获取的困难，本研究只采用了表层温度、叶绿素a浓度、表温梯度强度和叶绿素a梯度强度4个要素，在今后的研究当中，尚需要将更多的环境因子，如海流、盐度等，甚至临近时空的环境因子也加入模型当中，以提高西北太平洋柔鱼渔场的预报精度。

致谢:向提供海表温度数据、叶绿素a浓度数据的发布机构NASA表示诚挚的谢意。

[1] 酒井光夫, 若林敏江, 加藤慶樹． 平成23年度国際漁業資源の現況-アカイカ北太平洋 [D]． 横浜： 水産庁· 水産総合研究センター， 2012．

[2] 陈新军， 陆化杰， 刘必林， 等. 大洋性柔鱼类资源开发现状及可持续利用的科学问题 [J]. 上海水产大学学报, 2012， 21(5): 831-840.

[3] Yatsu A, Tanaka H, Mori J. Population structure of the neon flying squid, Ommastrephes bartramii, in the North Pacific [C].//Okutani T. Contributed Papers to International Symposium on Large Pelagic Squids. Tokyo: Japan Marine Fishery Resources Research Center, 1998: 31-48.

[4] Chen C S, Chiu T S.Variations of life history parameters in two geographical groups of the neo flying squid, Ommastrephes bartramii, from the North Pacific [J]. Fisheries Research, 2003, 63: 349-366.

[5] 陈新军, 曹杰, 刘必林, 等. 基于贝叶斯Schaefer模型的西北太平洋柔鱼资源评估与管理 [J]. 水产学报， 2011, 35(10)： 1573-1581.

[6] 陈新军， 刘必林， 田思泉， 等． 利用基于表温因子的栖息地模型预测西北太平洋柔鱼渔场 [J]． 海洋与湖沼， 2009, 40(6): 707-713.

[7] Zainuddin Mukti.Skipjack tuna in relation to sea surface temperature and chlorophyll-a concentration of bone bay using remotely sensed satellite data [J]. Journal Ilmu dan Teknologi Kelautan Tropis, 2011, 3(1): 82-90.

[8] 樊伟， 崔雪森， 沈新强. 西北太平洋巴特柔鱼渔场与环境因子关系研究 [J]. 高技术通讯， 2004, 14(10) ： 84-89.

[9] 陈雪忠， 樊伟， 崔雪森， 等． 基于随机森林的印度洋长鳍金枪鱼渔场预报 [J]. 海洋学报， 2013， 35(1): 158-164.

[10] He R, Chen K, Moore T, et al. Mesoscale variations of sea surface temperature and ocean color patterns at the Mid-Atlantic Bight shelfbreak [J]. Geophysical Research Letters， 2010, 37(9)： 1-5. doi: 10.1029/2010GL042658.

[11] 金龙, 黄小燕, 史旭明. 复共线性关系对逐步回归预报方程的影响研究 [J]. 气象学报, 2008, 66(4): 547-554.

[12] 吴云芳, 李珍照, 徐帆， 等. 因子相关性对两种大坝监测模型的影响分析 [J]. 武汉大学学报工学版, 2004, 37(1): 36-40.

[13] 陈新军， 高峰， 官文江， 等. 渔情预报技术及模型研究进展 [J]. 水产学报， 2013(18): 1270-1280.

[14] Tian Siquan, Chen Xinjun, Chen Yong, et al. Standardizing CPUE ofOmmastrephesbartramiifor Chinese squid-jigging fishery in the northwest Pacific Ocean [J]. Chinese Journal of Oceanology and Limnology， 2009, 27(4): 729-739.

[15] Ismail A I, Morrison E C, Burt B A, et al. Natural history of periodontal disease in adults: findings from the Tecumseh Periodontal Disease Study, 1959-87 [J]. J Dent Res， 1990, 69(2): 430-435.

[16] Pi Qingling, Hu Jianyu.Analysis of Sea Surface Temperature Fronts in the Taiwan Strait and its Adjacent Area Using an Advanced Edge Detection Method [J]. Science China Earth Science,2010, 53(7): 1008-1016.

[17] 沈新强, 王云龙， 袁骐， 等. 北太平洋柔鱼渔场叶绿素a分布特点及其与渔场的关系 [J]. 海洋学报， 2004， 26(6): 118-123.

[18] 唐峰华， 崔雪森， 樊伟， 等. 北太平洋柔鱼渔获量与海洋环境关系的遥感学研究 [J]. 海洋技术， 2011， 18(2): 78-82.

[19] Taro Ichii, Kedarnath Mahapatra, Mitsuo Sakai, et al. Differing body size between the autumn and the winter-spring cohorts of neon flying squid (Ommastrephes bartramii)related to the oceanographic regime in the North Pacific: a hypothesis [J]. Fisheries Oceanography， 2004, 13(5): 295-309.

[20] Yatsu Akihiko, Watanabe Tomowo, Mori Junta， et al. Interannual variability in neon flying squid abundance and oceanographic conditions in the central North Pacific, 1982-1992 [J]. Bull Nat Res Inst Far Seas Fish, 1996， 33: 123-138.

[21] 陈朝大， 梁柱勋， 郑士基. 一种利用关联规则的改进朴素贝叶斯分类算法 [J]. 计算机系统应用， 2010， 19(11)： 106-109.

[22] Hyvärinen A. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis [J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634.

[23] Mia K Stern, Joseph E Beck. Beverly Park Woolf. Using a Naive Bayes Classifiers for User Modeling [D]. Banff: Proceedings of the Conference on User Modeling, 1999.

[24] Domingos P, Pazzzani M. On the optimality of Simple Bayesian Classifier under zero-one Loss [J]. Machine Learning， 1997, 29: 103-130.

[25] Fan L W, poh K L, Zhou P. Partition-conditional ICA for Bayesian classification of microarray data [J]. Expert Systems With Applications, 2010, 37(12): 8188-8192.

[26] 张衡， 崔雪森， 樊伟. 基于遥感数据的智利竹荚鱼渔场预报系统 [J]. 农业工程学报， 2012， 28(15): 140-144.

[27] Cohen J. A Coefficient of Agreement for Nominal Scales [J]. Educational and Psychological Measurement, 1960, 20(1): 37-46.

[28] Brennan R L， Prediger D J. Coefficient Kappa: some uses, misuses, and alternatives [J]. Educational and Psychological Measurement, 1981, 41(3): 687-699.

[29] 陈新军， 田思泉. 西北太平洋海域柔鱼的产量分布及作业渔场与表温的关系研究 [J]. 中国海洋大学学报： 自然科学版， 2005, 35(1): 101-107.

[30] Ichii T, Mahapatra K, Okamura H, et al. Stock assessment of the autumn cohort of neon flying squid (Ommastrephes bratramii) in the North pacific based on past large-scale high seas driftnet fishery data[J]. Fish Res, 2006, 78: 286-297.

[31] 崔雪森， 伍玉梅， 张晶， 等. 基于分类回归树算法的东南太平洋智利竹荚鱼渔场预报 [J]. 中国海洋大学学报： 自然科学版， 2012， 42(7-8): 53-59.

[32] 范江涛， 陈新军， 钱卫国， 等. 南太平洋长鳍金枪鱼渔场预报模型研究 [J]. 广东海洋大学学报， 2011， 31(6)： 61-67.

[33] Tian S Q, Chen X J, Chen Y, et al. Evaluating habitat suit-ability indices derived from CPUE and fishing effort data for Ommatrephes bratramii in the northwestern Pacific Ocean [J]. Fish Res, 2009, 95: 181-188.

[34] Igarashi H, Awaji T, Ishikawa Y, et al. Development of a habitat suitability index model for neon flying squid by using 3-D ocean reanalysis product and its practical use [R/OL]. (2013-12-5)[2013-12-28]. http://www.jamstec.go.jp/j/pr/publication/jamstec_rrd/img/20131205. pdf.

责任编辑 朱宝象

The Establishment of Northwest PacificOmmastrephesbartramiiFishing Ground Forecasting Model Based on Naive Bayes Method

CUI Xue-Sen, TANG Feng-Hua, ZHANG Heng, WU Yu-Mei, FAN Wei

(The Key Laboratory of East China Sea & Oceanic Fishery Resources Exploitation and Utilization，Ministry of Agriculture, East China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences, Shanghai 200090, China)

Northwest Pacific is an important fishing ground ofOmmastrephesbartramiifor China. The accurate prediction of fishing grounds is critical to energy saving and catch increasing. In this study, a squid fishing ground forecasting model was built with Naive Bayesian method according to the historical catching, spatio-temporal and marine environmental data of this region. The environmental data included sea surface temperature (SST), concentration of chlorophyll ( (CHL), SST gradient strength and CHL gradient strength collected from 2002 to 2011. In order to satisfy the conditional independence assumption of naive Bayes method, the independent component analysis was carried out. By maximizing the Cohen′s Kappa coefficient, three-type CPUEs prior probabilities were determined for the Naive Bayesian forecasting model. As a test, the forecasted fishing ground maps were overlapped with the practical fishing grounds found from July to November 2012. Such an overlapping showed that the average comprehensive accuracy of forecasted fishing grounds was 69.9%, indicating that the Naive Bayesian model was effective for and feasible in forecasting the squid fishing grounds in northwest Pacific.

independent component analysis; naive Bayes method; fishing ground forecasting;Ommastrephesbartramii

国家科技支撑计划项目(2013BAD13B01)；中央级公益性科研院所基本科研业务费专项项目(2012T07)资助

2013-11-08；

2014-03-29

崔雪森(1973-)，男，副研究员。E-mail:cuixuesen@eastfishery.ac.cn

❋❋ 通讯作者： E-mail: wym_07@163.com

S931.3

A

1672-5174(2015)02-037-07

10.16441/j.cnki.hdxb.20130413