要在理解教材的基础上科学设计教学*
——从一个教学设计案例说起
2015-03-17浙江省仙居县教研室吴增生
☉浙江省仙居县教研室 吴增生
要在理解教材的基础上科学设计教学*
——从一个教学设计案例说起
☉浙江省仙居县教研室 吴增生
人教版义务教育初中数学教科书(2012年版)是基于义务教育数学课程标准(2011年版),由多名学科专家、教育专家、教研员和一线教师组成的团队,经过多年研究形成的权威、可靠的课程资源.它反映了新的课程标准的要求、数学学科的本质、学生的数学学习规律,在此基础上设计教学基本思路和经典有效资源.科学、有效的教学设计方案,建立在理解数学、理解学生、理解教学的基础上.这三个理解,既反映在课程标准上,也具体地反映在教材上.在深刻理解教材的基础上,才能设计出好的教学方案,取得良好的教学效果,否则,就会出现教学偏差,教学效果就会打折扣.
一、一个真实而有争议的教学案例
教学内容:3.4实际问题与一元一次方程(1).
整体教学思路:以环保出行引出自行车问题:问题1—问题2—问题3-反思总结.
1.提出问题
环境保护是我国当前面临的突出问题,自行车是环保的交通工具.某企业生产自行车,请帮助该厂解决生产安排问题.
问题1:车间1有22个工作组,每组每天能生产车座12个或车轮20个,如果自行车一个车座配两个车轮,为了使每天生产的车座和车轮配套,应怎样安排生产车座和车轮的工作组个数?
2.分析问题,解决问题
教师引导学生在下面的表格中先填上已知量,再设出未知数,把表格填完整:

每组生产数组数产量车座1 2 x 1 2 x车轮2 0 2 2 -x 2 0(2 2 -x)
师:怎样找等量关系?
生1:一个车座和两个车轮配套.
师:两个车座呢?
生1:4个车轮.
师:10个车座呢?
生1:20个.
师生共同找到等量关系:车座数∶车轮数=1∶2.
师:你能用这个等量关系列出方程吗?
生2:2×12x=20(22-x).
师:请用最快速度解一下这个方程.
学生3解方程,在学生解方程的过程中,教师反复追问学生每一步变形的依据.
(学生完成解题后)
师:刚才的解题过程分哪些步骤进行?
生(齐):设未知数、列方程、解方程.
师:能把结果和方法应用到其他问题上吗?
问题2:车间有21个工作组参加工作,每组每天能生产车座12个或车轮20个,如果要生产三座自行车,3个车座配2个车轮,为使每天生产的车座和车轮配套,应安排车座和车轮工作组各几个?
师:请思考下面问题:(1)已知量是什么?(2)未知量是什么?(3)能找到已知量和未知量的等量关系吗?(4)能否验证你的结论?(5)能否把结果和方法应用于其他问题吗?
生4分析问题,列表如下:

每组生产数组数产量车座12x12x车轮2021-x20(21-x)
生4的方程:2×12x=3×20×(21-x).
生5的方程:3×12x=2×20×(21-x).
教师引导学生辨别方程的对错,在此基础上解出方程,确定答案.
3.应用拓展
问题3:某车间有22个工作组,专业生产自行车配件:螺栓和螺母,每组每天能生产120个螺栓或200个螺母.第一天分别安排11个工作组生产螺栓和螺母,螺栓和螺母按照1∶2配套.问:第二天怎样安排生产螺栓和螺母的组数,才能使这两天生产的螺栓和螺母配套?
教师引导学生列出方程解决问题.
4.课堂小结
教师与学生一起总结本课学习内容.

这是一堂区域比赛课,对本课出现了两种截然不同的评价.A.很好,能创设符合学生实际的情境,重视等量关系分析,能进行有效的变式训练.B.不好,是题型训练,而不是思想方法的教学,没有有效达成教学目标.那么,究竟是好还是不好?
二、课例评析
(1)要评价一堂课好不好,涉及“好课”的评价标准.不同的人基于不同的专业研究视野,对“好课”的理解不同.如顾明远教授认为“深入浅出”(轻负高效)的课是好课;崔允灏教授认为好课的标准是“教得有效,学得愉快,考得满意”;叶澜教授认为好课的标准是“(1)有意义的课——扎实的课;(2)有效率的课——充实的课;(3)有生成性的课——丰实的课;(4)常态下的课——平实的课;(5)有待完善的课——真实的课”.虽然对“好课”有不同视角的理解,但基本上都涉及“教学内容和目标”“课堂生态”“课堂教学的效果”这三个部分,“好课”标准具有科学性,其本质要求是最大限度地使学生快乐,更有效地促进学生的发展;具有学科性,不同的学科有不同的专业视角;具有时代性和发展性,会随着时代变迁而发展.数学好课首先应该是“内容恰当,目标合理”,其次是“简约厚重,突出重点”,第三是“合理启发,突破难点”,第四是“学生有效参与,探究生成”,第五是“目标达成,认知发展”.这些要求可以用图1来表示.

图1
(2)要使一堂课达到上述要求,需要建立在理解数学、理解学生、理解数学教学这“三个理解”的基础上设计教学,这样才能保证教学设计的科学性,避免盲目性.人民教育出版社中学数学编辑室的“核心内容及其思想方法教学设计研究”的成果——“六环节”教学设计流程是达成“三个理解”、进行科学设计的工作机制保证.
按照“核心内容及其思想方法教学设计”的“六环节”工作程序,教学设计需要进行“内容和内容解析”“目标和目标解析”“教学问题诊断分析”“教学支持条件分析”,在这些分析的基础上明确核心内容和目标,把握重点和难点,明确总体思路和支持条件;然后进行“教学过程设计”,以保证核心内容及其思想方法的教学落实,突出重点,突破难点,形成以问题为导向的系统、有效的教学方案;最后,进行“目标检测设计”,检验教学效果.
(3)按照“六环节”教学设计流程,内容、目标和教学问题分析如下所示.
①内容和内容解析.
内容:“实际问题与一元一次方程”第1课时,两个例题(配套问题和工程问题),方程建模的步骤、方法、要点概括.
内容解析:方程理论是代数中的核心内容,初中方程的主要内容包括一元一次方程、二元一次方程组、一元二次方程、分式方程等.初中阶段方程内容的重点是:怎样解方程,怎样列方程,突出模型属性.一元一次方程是最简单的方程,是继续学习其他方程的基础.本章的重点是一元一次方程的解法和应用,核心的思想方法是转化思想和模型思想.
本章先安排了方程的相关概念,然后安排了方程的解法,再安排学习用一元一次方程解决实际问题.为了突出模型思想,突破方程建模难点,在方程的概念和解法的内容中,从实际问题出发提出研究内容,让学生先进行模仿操作,在学习完方程的概念和一元一次方程的解法后,集中安排用一元一次方程解决实际问题的学习,让学生进行方程模型运用的明朗化概括,再让学生集中进行运用方程建模的思想解决问题的训练,发展学生应用一元一次方程解决实际问题的能力(如图2).

图2
本节课内容是:从解决两个不同数量关系的例子中概括出用方程模型表述和解决问题的基本步骤、基本思想方法和要点.例子是让学生用方程解决不同的问题,是为了让学生经历做事情的过程,重点是让学生概括做事情的套路,即用方程模型解决问题的基本步骤、思考方法和注意要点.因此,本内容本质上是数学思想方法的教学.
②目标和目标解析.
目标:(i)经历根据配套问题和工程问题中的数量关系列方程的过程;(ii)探索用一元一次方程解决问题的步骤、思想方法和要点;(iii)体会方程是刻画现实世界中的数量关系的有效模型,体会模型思想.
目标解析:目标(i)要求能分析配套问题和工程问题中的数量关系,列出方程;目标(ii)要求学生能通过问题解决后的反思总结,概括出用一元一次方程模型解决问题的步骤、方法和要点;目标(iii)要求学生通过解决问题和解决问题后的反思总结活动,体会用方程模型解决问题的有效、简约、清晰,体会方程是联系已知和未知的桥梁.
③教学问题诊断分析.
学生已经基本形成了解一元一次方程的计算技能;学生在先前的学习中积累了一些列方程解应用题的经验,已经经历了方程建模思想的操作体会阶段,根据数学思想方法学习的“操作体会、明朗化、自觉运用、联系发展”的四阶段发展规律,需要让学生通过反思和总结,用自己的语言概括出用一元一次方程模型解决问题的“套路”(步骤、方法和要点),然后在后继学习中进行专项训练,再在不同的方程模型中继续训练,相互联系.
“会学着做”和“会说出做的步骤、方法、要点”是不同的认知层次,前者是不自觉的行动,是“摸着石头过河”,后者需要对自己的行为进行概括和总结,概括“套路”,并用自己的话说出来,这是难点.
根据教科书的内容安排,本课学习的重点是概括建立一元一次方程解决实际问题的套路:步骤、方法、要点,不是训练某一种应用题的题型.但该教学过程中选择了配套问题题型变式训练的教学方法,这显然不是本内容的重点.本课的内容选择不当、目标及重点和难点定位错误,导致教学过程变成了题型训练.解决一种数量关系的题型训练的是一种小技巧,而形成用方程模型解决问题的套路则是大智慧.忽视大智慧,追求小技巧,这使得本来应该达成的核心教育价值没有达成,顾左右而言它,捡到芝麻,丢了西瓜.
没有认真分析教材编写体系,没有理解教材编写意图,是出现忽视重点、顾左右而言它的症结所在.这种现象在教学实践中相当普遍.
三、改进建议
在前面内容和内容解析、目标和目标解析、教学问题诊断分析,明确内容的核心和重点,合理定位目标,明确学情和难点的基础上,进行如下的改进设计.
1.解决问题,唤醒经验
问题1: 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
师生活动:教师引导学生在阅读问题、分析数量关系的基础上,列出方程解决问题.
追问1:能说说“每人每天可以生产1200个螺钉或2000个螺母”及“生产的螺钉和螺母刚好配套”这两句话的意思吗?
追问2:每天生产的螺钉总数和螺母总数是怎样计算的?
追问3:每天生产的螺钉总数和螺母总数有什么等量关系?
设计意图:通过解决具体问题,唤醒列方程和解方程的操作经验.通过追问帮助学生理解问题中关键语句中的数量关系,找到问题中的等量关系.学生在教师的启发下,经历如下的从定性分析到定量分析的思考过程,寻找相等关系列出方程(如图3).

图3
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得:2×1200x=2000(22-x).
解方程,得:6x=5(22-x).
11x=110.
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
2.初步反思,总结经验
问题2:上述问题解决过程中经过了哪些步骤?是怎样想的?
师生活动:教师引导学生总结出解决问题的基本步骤:设(设未知数)、列(列一元一次方程)、解(解一元一次方程)、检(检验解的意义)、答(确定实际问题的答案).思考的方法如图4所示.

图4
3.再解问题,反思总结
问题3:整理一批图书,由一个人做要40h完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应该安排多少人工作?
师生活动:教师引导学生仿照问题1,独立解决问题,教师对有困难的学生或小组进行指导.
设计意图:再次操作,积累经验,为方程思想的概括提供典型样例.
问题4:这个问题的解决过程中又经过了哪些步骤?
师生活动:类似于问题2的活动,教师引导学生再总结本题的解题步骤和思考方法,得到图5.
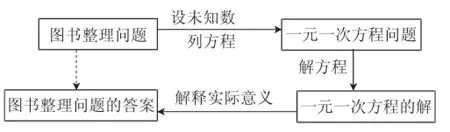
图5
4.抽象概括,形成步骤和方法
问题5:综合两个例题的解决过程,你能总结出用一元一次方程解决实际问题的一般步骤吗?
师生活动:教师引导学生比较两个例子的解题步骤和思想方法,忽略问题的类型,抽象出用一元一次方程解决实际问题的步骤和方法(如图6).

图6
追问:在这两个例题的解决过程中,你认为要列出方程的关键是什么?
设计意图:把具体问题解决过程的步骤和方法一般化,使之成为能迁移到新情境中的典型方法:方程建模思想.实现数学思想方法从模仿操作到明朗化的认知飞跃.
5.巩固训练,目标检测
练习1:一套仪器由一个A部件和三个B部件构成.用 1m3钢材可以做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
练习2:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
课后作业:教科书习题3.4第2、3、4、5题.
设计意图:让学生用概括得到的步骤和思想方法指导解决新的问题,巩固步骤、方法,同时检测学生能否运用得到的步骤和方法解决问题,评价本课的教学效果.
四、进一步的思考
由上述案例可知:在没有深入分析教材和深刻理解教材的情况下凭感觉、凭经验、凭空想进行教学设计是造成教学过程中忽视重点、杂乱臃肿、顾左右而言它、效率低下的主要原因.教学设计中的这种现象比较普遍地存在,集中体现为两种基本形态:一是形式化地搬教材和解释教材;二是在没有深刻理解的情况下随意更改,乱“创新”.
分析教材要分析什么呢?首先要整体分析知识体系,明确承载的教育价值,确定合理的目标,明确重点和难点;其次要分析教材内容中所蕴含的数学思想方法;第三要分析教材中所设计的学习活动,明确设计这些活动的意图及其作用.
分析教材的方法有:整体阅读教材、系统把握知识关联;重点阅读当前内容和课程标准,准确把握地位和作用,确定合理目标;阅读教材引言、小结和教师用书,理解教材编写意图.
要进行科学设计,需要在理解教材的基础上用好教材,基本的做法是:(1)理解教材、尊重教材,在没有充分依据的情况下不随便更改教材的教学设计思路和教学资源;(2)用“核心内容及其思想方法设计”的“六环节”工作程序保障教学设计的科学性,避免盲目性;(3)目标导向,问题任务驱动,进行教材资源的活动化设计;(4)分析学情,做好教材资源本土化设计;(5)整体布局,进行教学活动的系统化设计;(6)在充分理解、深入研究的基础上慎重而有依据地更改教材资源,创新设计.
1.课程教材研究所.义务教育教科书(七年级上册)[M].北京:人民教育出版社,2014.
2.吴增生.数学思想方法及其教学策略初探[J].数学教育学报,2014(3).Z
*本文为作者在人教社2015年全国培训会议上的发言(有修改).基金项目:浙江省2014年教育科学规划课题:基于脑、适于脑和发展脑的数学教学实践研究(2014SC295).
