重视课本资源,促进数学发现
——一道“幻方填数题”的教学及反思
2015-03-17江苏省南通市虹桥二中汤
☉江苏省南通市虹桥二中汤 双
重视课本资源,促进数学发现
——一道“幻方填数题”的教学及反思
☉江苏省南通市虹桥二中汤 双
近读《中学数学》,不少教师针对离开教材搞教学的现象多有批判,以笔者所见,当前由于所谓的“导学案”的流行,有些同行确实把教材置于一旁,只是组织学生练习导学案、教辅资料,对教材的研究不够,特别是对教材上一些特色栏目缺少关注和研究.本文结合新人教版七年级上册第21页“实验与探究”中的一道幻方填数题,谈谈在教学过程中引导学生展开发现式学习,实现神机妙算的一些做法,提供研讨.
一、教学案例
教材原题:有人建议向火星发射如图1所示的图案,它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.同一横行、同一竖列、同一斜对角线上的3个数相加都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).

图1

图2
你能将-4,-3,-2,-1,0,1,2,3,4这9个数分别填入如图2所示的幻方的空格中,使每一行、每一列、每一条斜对角线上的3个数之和相等吗?
教学时,笔者将要求降低,要求学生将1、2、3、4、5、6、7、8、9这9个数分别填入图2的9个空格中,使得每一行、每一列、每一条斜对角线上的3个数的和相等.
经过猜想、推理、修正、论证,学生发现在具体填数时,首先应确定关键位置,也就是最中间的空格.
师:为什么?
生1:因为它参与的运算最多,而且关键位置上的数字应该是5.
师:为什么是5呢?
生2:刚开始是猜的,后来根据想法继续论证,我发现这9个格子以中间一格为中心形成一个十字架,画出十字架的对角线形成一个米字格,且米字格上的数和为60,而这9个数的和为45,所以关键位置多算的3次和为60-45=15,因而求出最中间一格的数字为5.
生3:其次,根据题目中要满足每行、每列、每条斜对角线三数之和为15这个条件,中间一格数字是5,所以每行、每列、每一斜对角线剩余两数之和只可以为10.在这9个数中,我发现1与9,2与8,3与7,4与6关于5成对称分布,且它们的和也为10,我就可以将它们填入剩余的8个格子中,从而得出其中的1种填法(如图3).
教师:刚才这位同学的解法,正确吗?还有不同的填法吗?

图3
学生讨论产生了另外7种填法(如图4~图10),其中,图9就是图1.
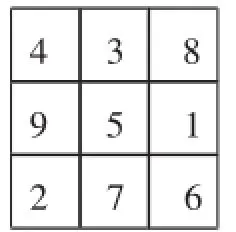
图4
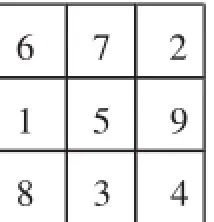
图5
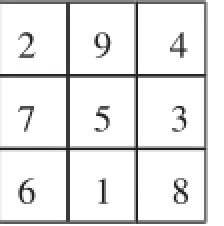
图6
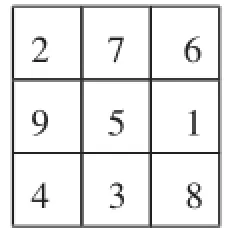
图10
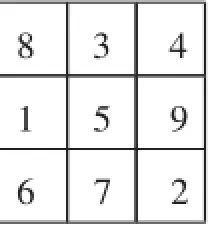
图8

图9

图7
案例解读:著名的数学大师波利亚曾在谈论教学法时说过:“我们可以在学生对问题思考前让学生猜想该题的结果或部分结果.为了验证猜想,学生会专注在课堂教学中,主动关注题目,关心课堂进展,他就不会打盹或搞小动作.”这就是说,作为一名数学教师,置身于数学发现学习的过程中,对于一个“新的”数学问题,我们应该带领学生一起猜想、证明,也许此时这个数学理论的形成过程、解决过程并非与数学家们的推出过程一致,甚至可能存在一些偏差,然而,这样的数学教学才更能激活学生的思维,才是数学学习的本质所在.
二、教学反思
1.重视解题回顾,促进学生深刻理解
升入初中,数学的解题思维与小学解题思维发生了较大变化,如果说小学数学教学侧重于形象思维训练,那么初中数学教学则侧重于抽象思维训练.对于刚刚升入初中的学生来说,很多题目他们都不知道怎么“下手”解决,此时,需要我们把思维想给学生听,并确保学生听懂.例如上面的三阶幻方填数题,通过讨论,虽然得出8种满足题目要求的不同填法,但不代表所有同学都掌握了本题的解答要领,更不代表今后每位同学遇到类似的题型可以独立解决,此时挑出几位已经掌握思考方法的同学阐述他们的思考过程、归纳解决此类问题的方法是十分必要的.下面是两个学生的解后反思.
生4:请大家仔细观察一下,不难发现,如果以图3为标准,那么图4可以通过图3绕中心顺时针旋转90°得到,由此可得,在前四幅图中,相邻两幅图中的后一幅都可以由前一幅绕中心顺时针旋转90°得到.
生5:大家可以对照观察一下,我们发现上组解法中的任意一个互换左、右列便可在下组中找到相应的结果,如图3左右列互换便可得到图7,同理,其余三组也有此规律.后来,我们又发现图3与图9,图4与图7,图5与图10,图6与图8,是通过互换上、下行得到的.
案例解读:经过修改后,问题起点低,具有普适性,让不同层次的同学都有思考的时间和空间,每一位同学都可以主动地与原有的知识经验相联系,结合自己的思维特点,积极参与到课堂教学活动中,使得问题与学生已有的认知结构建立实质性联系,变“被动防守”为“主动进攻”,给学生思考问题提供了一种全新的思维模式,为实现神机妙算搭建了一个新平台.
2.用好课例素材,促进学生发现
我们知道,数学既是发现,又是发明.事实上,由于选择了教材上这道幻方填数题,师生围绕这道题开展解题学习占去一个课时,但是在这个过程中,笔者要求学生把1至9这9个数从不同的途径填入相关空格中,在探索解法的过程中完成了一次思维革命.如果此时将原题后半部分要求加进去,将这9个数变为-4~4,又有几种填法呢?有了刚才的经历,此刻,相信绝大部分学生在这种思维模式的指导下,经过思考、交流、猜想、倾听、验证等环节,发现-4~4这9个数对应的可以由1至9这9个数依次减5得到,所以只需将图3~图10中的9个数分别减5,就可以求出8种满足条件的填法.当然,探究出规律后,还可以继续启发学生探究,如果将这9个数同时加同一个数后,能使每一行、每一列、每一条斜对角线上的三数之和相等吗?如果将这9个数分别扩大相同倍数,能使每一行、每一列、每一条斜对角线上的三数之和相等吗?如果将这9个数同时乘方,能使每一行、每一列、每一条斜对角线上的三数之和相等吗?
有的学生很难接受理性、抽象、客观的思维,他们习惯凭借感觉和经验对问题做出判断,拒绝成长.如果每天能接受一点点理性、抽象、客观的思维,在解题的过程中能体会到一点点方法的、思维的、抽象的、客观的、归纳的力量,笔者有理由相信这种教学方法将激发出学生无穷的潜力.
1.严莉.对一份“习题单”式导学案的商榷[J].中学数学(下),2014(11).
2.李庾南.自学·议论·引导教学论[M].北京:人民教育出版社,2013.
3.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).
4.章建跃.理解数学是教好数学的前提[J].数学通报,2015(1).
5.潘龙生.教学,少些一带而过[J].数学通报,2015(1).H
