温度影响下FGM圆环板的面内自由振动分析

滕兆春, 蒲 育

(兰州理工大学 理学院，兰州 730050)

温度影响下FGM圆环板的面内自由振动分析

滕兆春, 蒲 育

(兰州理工大学 理学院，兰州 730050)

基于二维弹性理论和Hamilton原理，假设材料物理性质随温度变化且沿圆环板径向按照幂律梯度分布，导出了温度影响下FGM薄圆环板面内自由振动的运动微分方程。用微分求积法(DQM)计算了温度影响下FGM圆环板面内自由振动的无量纲频率，并与各向同性材料圆环板面内自由振动的无量纲频率进行了比较，说明该分析方法的有效性。同时考虑了沿圆环板径向均匀升温和非均匀升温两种情况下，几何参数、材料性质和温度变化对面内自由振动频率的影响。

FGM圆环板；初始热应力；面内自由振动；无量纲频率；Hamilton原理；微分求积法

圆(环)板的面内自由振动，在工程领域中有十分重要的意义和广泛的应用背景。例如转动圆(环)板的转动噪音消除以及面内振动频率在压电圆片设计中的参考价值。此外，圆(环)板面内振动研究在工程中的车轮、盘式刹车片以及驱动器硬盘等结构元件中也具有潜在的应用。近些年，随着新材料的兴起，功能梯度材料作为一种新型复合材料，越来越多受到人们的关注。由于功能梯度材料在高的温度梯度环境下能减小热变形及缓解热应力，故功能梯度材料圆(环)板在核工业、船舶，航空航天和化学工业等领域受到广泛的应用，从而研究功能梯度材料圆(环)板的振动问题显得尤为重要。许多学者从不同的角度大量研究了各向同性材料圆(环)板的横向振动[1]，然而圆(环)板面内自由振动的研究相对较少[2-4]。文献[5]研究了厚板的面内振动，而文献[6]得出了夹支圆板面内自由振动固有频率方程的解析解。文献[7]研究了圆(环)板在四种经典边界条件下的面内自由振动，应用边界正交多项式特性和Rayleigh-Ritz法得出了固有频率和相应的振型。文献[8]研究了圆环板在内、外部弹性支承约束条件下的面内自由振动，得出增加固支支承点会引起不同高阶振型分化成两个不同的频率。文献[9]用Ritz法研究了均匀厚度超椭圆板的面内自由振动，引入Lagrange乘子以满足边界条件，并且得到了自由边界条件和点支承边界条件下椭圆板和矩形板等不同形状板的面内自由振动的无量纲频率。文献[10-11]基于von-Karman板理论，研究了热机载荷作用下，功能梯度圆板的非线性弯曲和过屈曲行为。文献[12]基于三维线弹性理论，用半解析法研究了FGM圆板物性参数沿厚度方向变化的自由振动和强迫振动。然而温度影响下FGM圆(环)板面内自由振动的研究目前在国内外还没有相关的文献报道。

这里研究了温度影响下FGM薄圆环板的面内自由振动问题。假设材料物性随温度变化，且材料组分沿圆环板径向按幂律梯度分布，首先基于二维热弹性理论，得到初始热应力，然后应用Hamilton原理和二维弹性理论推导出温度影响下FGM薄圆环板面内自由振动的控制微分方程。采用微分求积法非均匀节点将控制微分方程沿圆环板径向离散，同时也将相应的边界条件离散，将微分方程组转化为自由振动的特征值问题，从而求得面内自由振动的频率，并与已有的各向同性材料圆环板面内自由振动的无量纲频率进行了比较，证实所得的结果有效。最后研究了沿径向均匀升温和非均匀升温两种情况下，几何参数、材料性质和温度变化对频率的影响。

1 控制微分方程及参数的无量纲化

1.1 温度影响下功能梯度材料的物性关系

考虑厚度为h的FGM薄圆环板，设物性参数随温度变化，材料组分的体积分数沿径向按幂律梯度分布，且温度也沿径向分布，其弹性模量为E，密度为ρ，泊松比为μ，外半径为Ro，内半径为Ri，径向位移分量为u，周向位移分量为v，圆环板内部(r=Ri)为金属材料，外部(r=Ro)为陶瓷材料，功能梯度材料圆环板的物性参数P(弹性模量E，泊松比μ，密度ρ，热膨胀系数α，热传导率K)与径向坐标r和温度T满足

式中：p为梯度指标，下标m与c分别为金属和陶瓷。陶瓷和金属两种材料的某一物性参数G随温度T变化的函数关系为[13-14]：

G(T)=G0(1+G1T+G2T2)

(2)

式中：Gi(i=0,1,2)为材料系数。

1.2 初始热应力的计算

假设FGM薄圆环板内无热源，温度沿圆环板径向方向分布，由一维热传导方程

(3)

考察边界条件：r=Ri时，T=Tm

r=R0时，T=Tc

(4)

式(3)在边界条件式(4)下的解可由多项式表示为

(5)

式中:

当温度变化时，FGM圆环板内的初始热应力[14-15]

(6)

式中：σ0r,σ0θ,τ0rθ为初始热应力，ΔT=T-T0，T0为无应力状态时的温度。

(7)

1.3 自由振动分析

当圆环板达到热平衡状态后受外界一扰动(激励)，此时圆环板内任一点将在热平衡位置自由振动，设达到热平衡状态相对于未变形状态任意一点的初始位移分别为u0(r,θ)，v0(r,θ)，由于自由振动所产生的位移分别为u(r,θ,t)，v(r,θ,t)，则任意一点的总位移分别为：

由于考虑板内初始热应力的影响，应变满足

(8)

式中：上标L表示线性项应变，NL表示非线性项应变。线性项应变与位移之间的关系为

(9)

非线性项应变与位移之间的关系为

(10)

由二维弹性体本构关系

(11)

对圆环板应用Hamilton原理

(12)

(13)

圆环板弹性势能的变分为

(14)

当达到热平衡状态后，初始应变的变分δε0r=δε0θ=δγ0rθ=0，且τ0rθ=0。本文只考虑线性自由振动，故略去式(14)中乘积项的非线性高阶无穷小量，从而式(14)可简化为

(15)

将式(9)～式(11)，式(13)和式(15)代入式(12)，由变分原理及分部积分法可得温度影响下功能梯度材料薄圆环板面内自由振动的运动微分方程和相应的边界条件分别如下：

(16)

(17)

边界条件为

u=v=0

(18)

或

(19)

(20)

式中：n为环向波数，t为时间，i为虚数单位，ω为固有频率。将式(20)代入式(16)和式(17)，且无量纲化如下：

(21)

(22)

(23)

2 DQM离散及特征值问题

式(22)和式(23)系数中包含初始热应力项，且微分方程为变系数常微分方程组。许多实例已证实DQM作为求解变系数微分方程(组)的有效方法，具有离散节点个数较少、计算精度高、易收敛、工作量小等优点。采用DQM且参考文献[16]，FGM圆环板在径向方向的节点划分采用如下的公式：

(24)

其中N为节点总数。式(22)和式(23)用DQM分别离散后化为：

(25)

(26)

式中:Aij和Bij分别为一阶导数和二阶导数的权系数，且i=2,3,…,N-1，

考虑如下的两种基本边界条件：

(1) 夹紧 (C)

Un=Vn=0, 在x=β或1

(27)

(2) 自由 (F)

(28)

用DQM分别离散边界条件式(27)和式(28)得

Uni=Vni=0，i=1或N

(29)

(30)

将式(29)和式(30)对应组合后可得不同类型离散化后的边界条件：

内部夹紧-外部夹紧(C-C)

内部自由-外部自由(F-F)

内部自由-外部夹紧(F-C)

内部夹紧-外部自由(C-F)

控制式(25)～式(26)与边界条件式(29)～式(30)对应联立后便构成了不同边界条件下面内自由振动的边值问题。该边值问题可用分块矩阵形式表示为：

(31)

{wb}=[Un2,Un3,…,Un(N-1),Vn2,Vn3,…,Vn(N-1)]T
{wd}=[Un1,UnN,Vn1,VnN]T

式中:{wb}为圆环板内部的节点位移，{wd}为圆环板边界处的节点位移。[Sbb]和[Sbd]是由运动方程导出的刚度矩阵，而[Sdb]和[Sdd]是由边界条件导出的刚度矩阵。由式(31)消去{wd}，得自由振动的特征值问题

[S]{wb}-Ω2[I]{wb}={0}

(32)

式中:[S]=[Sbb]-[Sbd] [Sdd]-1[Sdb]，[I]为(2N-4)阶单位阵，特征向量{wb}描述了温度影响下FGM圆环板面内自由振动的振型。

3 计算结果与分析

计算中选取金属材料为Ti-6Al-4V，陶瓷材料为ZrO2，它们随温度变化的物性系数如表1所示[13-14]，其温度的适用范围为300 K≤T≤1 100 K。通过MATLAB语言编写的计算程序可获得方程式(32)特征值问题的无量纲频率。首先取节点个数N=17，泊松比μc=0.3，p=0，ΔT=0时，温度影响下FGM圆环板的面内自由振动问题退化为各向同性圆环板的面内自由振动问题。在表2和表3分别给出了C-C，F-C两种边界条件下各向同性材料圆环板振动的无量纲频率。将计算的结果与已有的研究数据[2,7]进行比较，其结果非常接近，取较少的节点数就能满足精度所需，工作量较小，说明DQM对于研究本问题的适用性和优越性。

表4和表5分别给出了不同梯度指标p在C-C，F-C边界条件下，均匀升温和非均匀升温时FGM圆环板的前三阶频率。从表中可以看出，频率Ω随环向波数n的增大而增大，随p的增大而减小；在相同参数下，均匀升温ΔT=800 K时的频率小于与非均匀升温ΔTm=0，ΔTc=800 K时相应的频率。

图1～图4分别给出了不同梯度指标p在C-C，F-C边界条件下，均匀升温和非均匀升温时FGM圆环板的一阶频率Ω1与内外半径比β之间的关系曲线。由图可见，频率随内外半径比β的增大而单调增大。图5和图6分别给出了C-C，F-C边界条件下均匀升温时FGM圆环板的前三阶频率Ω与梯度指标p之间的关系曲线。由图可见，Ω随p的增大而减小，减小程度由明显趋于缓慢，当p足够大时，Ω趋于常数。

图7～图8分别给出了不同梯度指标p在F-C边界条件下，均匀升温和非均匀升温时FGM圆环板的前三阶频率Ω与升温ΔT之间的关系曲线。比较图7和图8，不难看出，温度变化对频率影响较大。频率Ω随升温ΔT的增大而单调减小，而且升温相同时，均匀升温比非均匀升温对频率的影响更为显著，且这种差异程度随升温的增大而增大。

表1 金属(Ti-6Al-4V)和陶瓷(ZrO2)

表2 圆环板面内自由振动无量纲频率Ω (C-C)

表3 圆环板面内自由振动无量纲频率Ω (F-C)

表4 梯度指标p对于FGM圆环板在均匀升温时前三阶无量纲频率的影响(β=0.2，ΔT=800 K)

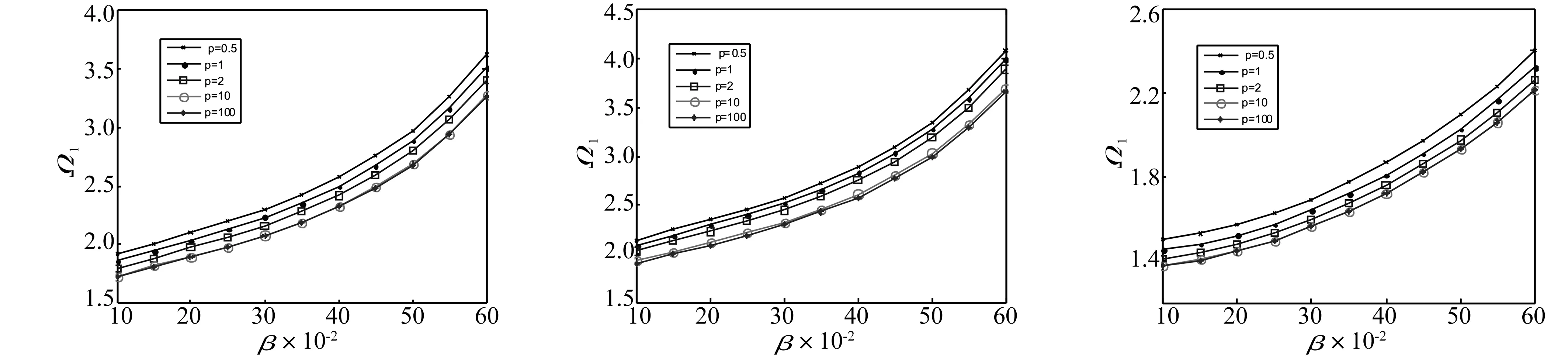
图1 C-C边界条件下均匀升温时一阶频率与内外半径比之间的关系曲线(ΔT=800K，n=1)Fig．1The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtouniformtemperaturerisewithclampedinnerandouteredges(ΔT=800K，n=1)图2 C-C边界条件下非均匀升温时一阶频率与内外半径比之间的关系曲线(ΔTm=0，ΔTc=800K，n=1)Fig．2The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtonon⁃uniformtemperaturerisewithclampedinnerandouteredges(ΔTm=0，ΔTc=800K，n=1)图3 F-C边界条件下均匀升温时一阶频率与内外半径比之间的关系曲线(ΔT=800K，n=1)Fig．3The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtouniformtemperaturerisewithfreeinnerandclampedouteredges(ΔT=800K，n=1)

图4 F-C边界条件下非均匀升温时一阶频率与内外半径比之间的关系曲线(ΔTm=0，ΔTc=800K，n=1)Fig．4The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtonon⁃uniformtemperaturerisewithfreeinnerandclampedouteredges(ΔTm=0，ΔTc=800K，n=1)图5 C-C边界条件下均匀升温时前三阶频率与梯度指标之间的关系曲线(ΔT=800K，β=0．2，n=1)Fig．5Thefirstthreedimensionlessnaturalfrequencyparametersvsmaterialgradedindexsubjectedtouniformtemperaturerisewithclampedinnerandouteredges(ΔT=800K，β=0．2，n=1)图6 F-C边界条件下均匀升温时前三阶频率与梯度指标之间的关系曲线(ΔT=800K，β=0．2，n=1)Fig．6Thefirstthreedimensionlessnaturalfrequencyparametersvsmaterialgradedindexsubjectedtouniformtemperaturerisewithfreeinnerandclampedouteredges(ΔT=800K，β=0．2，n=1)

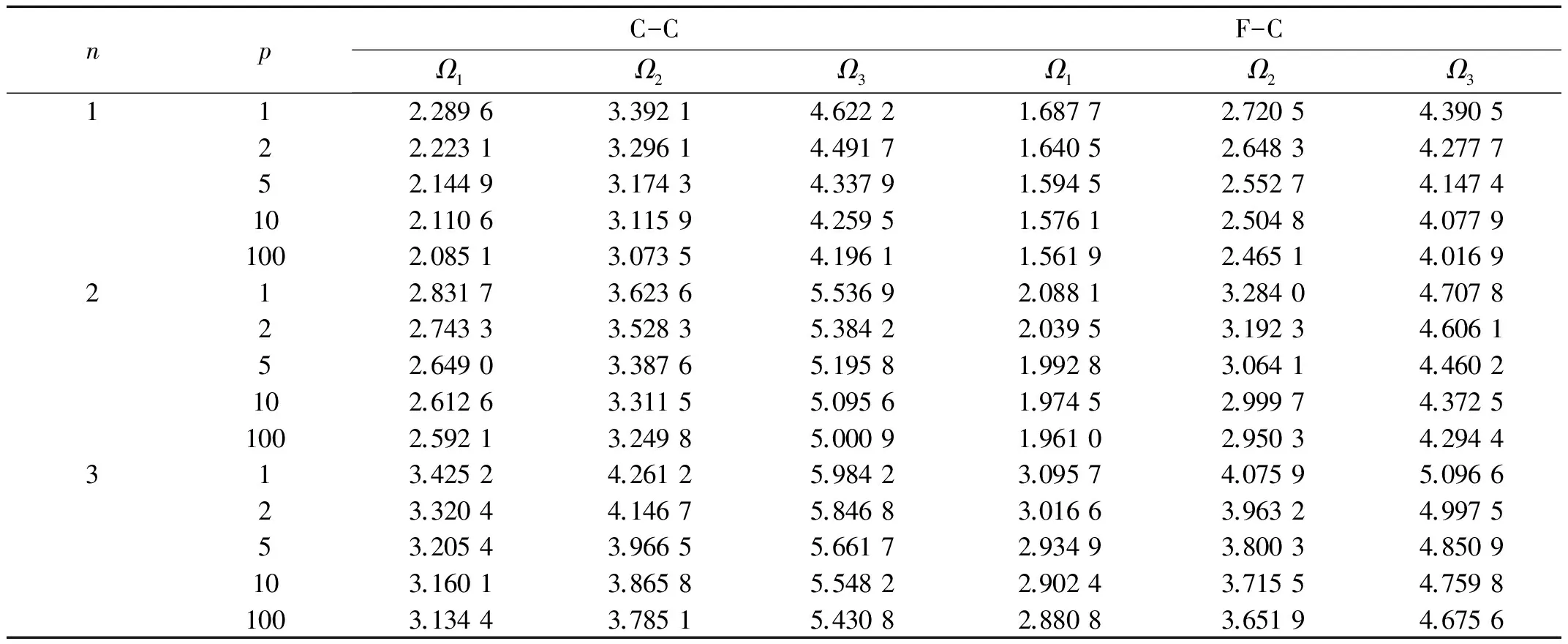
表5 梯度指标p对于FGM圆环板在非均匀升温时前三阶无量纲频率的影响(β=0.2，ΔTm=0，ΔTc=800 K )

图7 (a)～(c). F-C边界条件下均匀升温时前三阶频率与升温之间的关系曲线(ΔTc=ΔTm=ΔT，β=0.2,，n=1)Fig.7(a)-(c).The first three dimensionless natural frequency parameters vs uniform temperature rise with free inner and clamped outer edges(ΔTc=ΔTm=ΔT，β=0.2,，n=1)

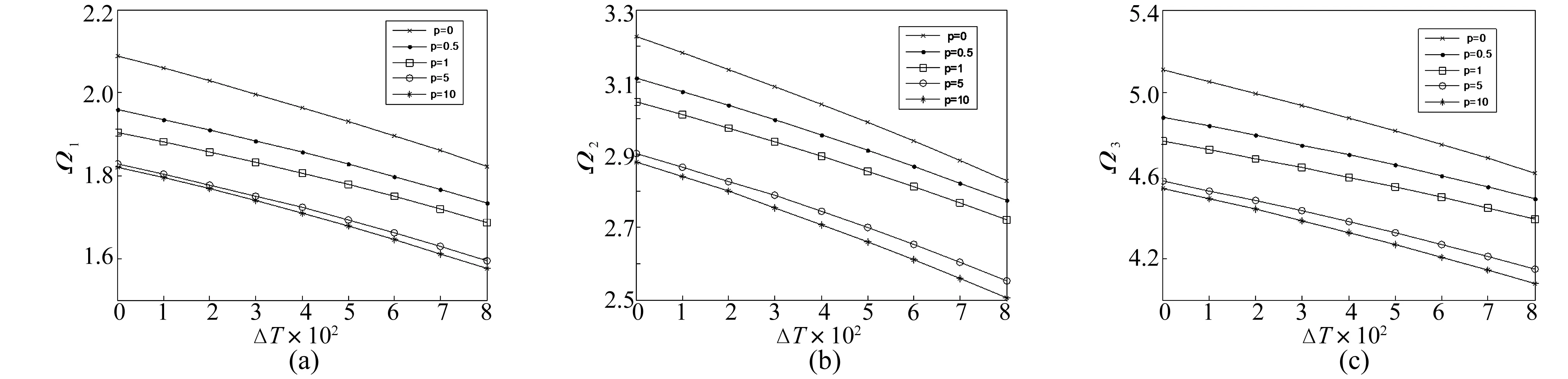
图8 (a)～(c). F-C边界条件下非均匀升温时前三阶频率与升温之间的关系曲线(ΔTm=0，ΔT=ΔTc，β=0.2，n=1)Fig.8(a)-(c). The first three dimensionless natural frequency parameters vs non-uniform temperature rise with free inner and clamped outer edges(ΔTm=0，ΔT=ΔTc，β=0.2，n=1)

4 结 论

本文基于二维热弹性理论，研究了温度影响下FGM薄圆环板的面内自由振动问题。假设材料物性随温度变化且沿圆环板径向按照幂律梯度分布，求得初始热应力，应用Hamilton原理得出面内自由振动的控制微分方程，用DQM获得了自由振动的无量纲频率，并将得到的结果与已有的各向同性材料圆环板频率进行了比较，说明本文的研究方法有效。最后研究了均匀升温和非均匀升温两种类型下，几何参数、材料性质和温度变化对无量纲频率的影响：频率随环向波数的增大而增大；随内外半径比的增大而增大；随梯度指标的增大而减小，减小程度由明显趋于缓慢，当梯度指标足够大时，频率趋于常数；温度变化对频率影响较大，且频率随温度的升高而单调减小；均匀升温与非均匀升温相比，在相同的边界条件下升温相同时，均匀升温对频率的影响更为显著。

[1] 杨志安, 冯宏伟. 电机端盖超谐共振分析[J]. 工程力学, 2012, 29(10):288-293. YANG Zhi-an, FENG Hong-wei. Superharmonic resonance of end-shields of electric machines [J]. Engineering Mechanics, 2012, 29(10): 288-293.

[2] Irie T, Yamada G, Muramoto Y. Natural frequencies of in-plane vibration of annular plates [J]. Journal of Sound and Vibration, 1984, 97 (1): 171-175.

[3] Farag N H, Pan J. Modal characteristics of in-plane vibration of circular plates clamped at the outer edge [J]. Journal of the Acoustical Society of America, 2003, 113(4): 1935-1946.

[4] 蒲育, 滕兆春, 房晓林. 圆环板面内自由振动的DQM求解[J]. 振动与冲击, 2013, 32(24): 152-156. PU Yu，TENG Zhao-chun, FANG Xiao-lin. In-plane free vibration of circular annular plates by differential quadrature method[J]. Journal of Vibration and Shock,2013,32(24):152-156.

[5] Tzou K I, Wickert J A, Akay A. In-plane vibration modes of arbitrarily thick disks [J]. Journal of Vibration and Acoustics, 1998, 120(2): 384-391.

[6] Chan II P. Frequency equation for the in-plane vibration of a clamped circular plate [J]. Journal of Sound and Vibration, 2008, 313(1-2,3): 325-333.

[7] Bashmal S, Bhat R, Rakheja S. In-plane free vibration of circular annular disks [J]. Journal of Sound and Vibration, 2009, 322(1-2): 216-226.

[8] Bashmal S, Bhat R, Rakheja S. In-plane free vibration analysis of an annular disk with point elastic support [J]. Shock and Vibration, 2011, 18(4): 627-640.

[9] Aletkin M. Free in-plane vibration of super-elliptical plates [J]. Shock and Vibration, 2011, 18(3): 471-484.

[10] Ma L S, WANG T J.Nonlinear bending and post-buckling of a functionally graded circular plate under mechanical and thermal loadings [J]. International Journal of Solids and Structures, 2003, 40(13-14): 3311-3330.

[11] Ma L S,Wang T J. Relationships between axisymmetric bending and buckling solutions of FGM circular plates based on third-order plate theory and classical plate theory [J]. International Journal of Solids and Structures, 2004, 41(1): 85-101.

[12] Nie G J, Zhong Z. Semi-analytical solution for three-dimensional vibration of functionally graded circular plates [J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(49-52): 4901-4910.

[13] Touloukian Y S. Thermophysical properties of high temperature solid materials [M]. New York: MacMillan, 1967.

[14] Kim Y W. Temperature dependent vibration analysis of functionally graded rectangular plates [J]. Journal of Sound and Vibration, 2005, 284(3-5): 531-549.

[15] Prakash T. Ganapathi M. Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method [J]. Composite Part B: Engineering, 2006, 37(7-8): 642-649.

[16] Bert C W, Malik M. Differential quadrature method in computational mechanics: A Review [J]. Applied Mechanics Reviews, 1996, 49(1): 1-28.

In-plane free vibration of FGM annular plates considering temperature effect

TENG Zhao-chun, PU Yu

(College of Science, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the two-dimensional elastic theory and the Hamilton’s principle, the differential motion equations for in-plane free vibration of the functionally graded material thin annular plate in thermal environment were derived. In the equations, the material properties were assumed to be temperature-dependent and graded in the radial direction of annular plates according to power law distributions. By using differential quadrature method(DQM), the dimensionless frequency parameters of in-plane free vibration of FGM annular plates under thermal environment were obtained. The formulations were validated by comparing the results with those available in literatures. Considering the cases of uniform and variable temperature rise distribution in the radial direction of annular plate respectively, the effects of geometrical parameters, material graded index and temperature rise on the natural frequencies of in-plane free vibration of annular plates were investigated.

FGM (Functionally Graded Material) annular plates; initial thermal stress; in-plane free vibration; dimensionless frequency; Hamilton’s principle; DQM

国家自然科学基金项目(11372123)

2013-10-29 修改稿收到日期：2014-05-29

滕兆春 男，硕士，副教授，1969年8月生

O343

A

10.13465/j.cnki.jvs.2015.09.037