基于最优广义S变换和脉冲耦合神经网络的轴承故障诊断

张云强， 张培林， 吴定海， 李 兵

(军械工程学院 车辆与电气工程系，石家庄 050003)

基于最优广义S变换和脉冲耦合神经网络的轴承故障诊断

张云强， 张培林， 吴定海， 李 兵

(军械工程学院 车辆与电气工程系，石家庄 050003)

针对滚动轴承故障信号具有明显的非线性和非平稳特征，提出一种基于最优广义S变换和脉冲耦合神经网络(PCNN)的故障特征提取方法。首先采用基于时频聚集性最优化的广义S变换获取轴承故障信号的时频表示，然后利用脉冲耦合神经网络对最优广义S变换时频图进行二值分解，提取二值图像的捕获比序列用于表达故障信号的故障特征。对滚动轴承4种状态信号进行分析，验证方法的有效性。结果表明该方法能够提取出更加有效的轴承故障特征参数，有利于提高轴承故障诊断的精度。

故障诊断；滚动轴承；特征提取；广义S变换；脉冲耦合神经网络

滚动轴承广泛应用各种旋转机械中，其运行状态往往严重影响设备整体性能的发挥，因此对滚动轴承进行故障检测和诊断具有重要的意义[1]。

当轴承出现故障时，振动信号中会出现周期性非平稳冲击成分，呈现出明显的非线性、非平稳特征[2]。时频分析方法在二维时频平面内对信号进分析，克服了传统的时域和频域分析方法在分析非平稳信号时不能同时获取信号的时域和频域信息的缺陷，广泛应用于机械设备故障诊断领域。目前，常用的时频分析方法有短时傅里叶变换(STFT)、伪魏格纳分布(WVP)、连续小波变换(CWT)和S变换(ST)[3-6]，然而这些方法都存在一些不足。短时傅里叶变换的窗函数固定，不利于分析非平稳轴承故障信号；伪魏格纳分布具有良好的时频聚集性，但存在交叉项干扰；小波变换尺度的大小与信号的频率没有良好的对应关系；S变换虽然结合了短时傅里叶变换和小波变换的优点，但其高斯窗函数的标准差固定为频率的倒数，导致信号高频部分的时频聚集性不是很理想。鉴于此，本文引入广义S变换(GST)[7-8]，并基于时频聚集性度量设计了一种最优广义S变换，用于获取轴承信号的时频表示。

轴承信号的时频图维数巨大，因此单纯的时频分析结果不能用于轴承故障诊断。故障信号进行时频变换后，还需要进一步提取特征。脉冲耦合神经网络(PCNN)具有良好的脉冲同步发放特性，在图像特征提取中具有无可比拟的优势[9-10]。因此，为了有效提取轴承故障信号特征，提出一种基于最优广义S变换和脉冲耦合神经网络的轴承故障特征提取方法。采用脉冲耦合神经网络对最优广义S变换矩阵进行二值分解，提取二值图像的捕获比序列作为轴承信号的特征参数，从而对轴承故障进行诊断。

1 广义S变换理论

1.1 广义S变换定义

广义S变换是对S变换的推广，可由基于高斯窗函数的短时傅里叶变换导出[11]。对于能量有限时间信号x(t)，短时傅里叶变换定义为：

(1)

其中:τ为微小的时间积分量；w(t)为高斯窗函数，其表达式为：

(2)

基于式(2)，广义S变换的窗函数的标准差σ定义为频率f的p次方的倒数，即σ=1/|f|p，其中p为调整参数，通常取(0,1]，则广义S变换可表示为：

(3)

当p=1时，广义S变换退化为S变换。由于广义S变换的窗口宽度也随着频率的增大而减小，所以在低频具有较高的频率分辨率，而在高频具有较高的时间分辨率。

1.2 最优广义S变换

广义S变换通过调节参数p可以有效改变高斯窗的宽度，从而改善时频分辨率，提高时频聚集性能。因此，广义S变换的时频聚集性能是否能达到最优，关键在于参数p的选择。文献[7]给出了一种时频聚集性的度量准则，定义为：

(4)

其中:GST(t,f)为能量归一化的广义S变换系数，即∑∑GST(t,f)=1；q为大于1的常数。

根据以上评价准则，设计一种基于时频聚集性最优化的广义S变换，计算步骤如下：

(1) 对于任意p∈(0,1]，根据式(3)对信号x(t)进行广义S变换；

(2) 对广义S变换系数进行能量归一化：

GST(t,f)=GST(t,f)/∑∑GST(t,f)

(5)

(3) 取q=2，根据式(4)计算广义S变换的时频聚集性M(p)；

(4) 通过最小化M(p)选取最优调节参数popt：

(6)

(5) 将p=popt代入式(3)，实现信号x(t)的最优广义S变换。

1.3 仿真信号分析

为了比较不同时频分析方法的时频聚集性，构造仿真信号x(t)：

x(t)=x1(t)+x2(t)+x3(t)+x4(t)
x1(t)=sin(20πt+2πt2)
x2(t)=sin(50πt·4t)
x3(250∶280)=sin[400πt(250∶280)]
x4(750∶780)=sin[400πt(750∶780)]

(7)

信号采样长度为1 024，采样频率为1 024 Hz。x(t)由1个线性调频分量、1个非线性调频分量和2个高频短时谐波分量组成，其时域波形如图1所示。图2为仿真信号经短时傅里叶变换、伪维格纳分布、S变换和广义S变换处理后的结果。

图1 仿真信号Fig.1 Time-domain waveform of the simulated signal

从图2中可以看出，短时傅里叶变换时频图在时间和频率上不能同时达到较好的分辨率，尤其是两个高频短时谐波分量的时频聚集性较差，几乎不可分辨；伪维格纳分布由于受交叉项的影响，4个信号分量在图中很难辨别；信号经S变换后虽然各个分量能够较清楚地辨别，但是高频部分的时频聚集性很差；而最优广义S变换时频图中各个分量不仅可以清晰显示，而且不同分量的时频聚集性都令人比较满意。因此，与其它时频方法相比，最优广义S变换的时频聚集性最好，更加适合于处理非平稳信号。

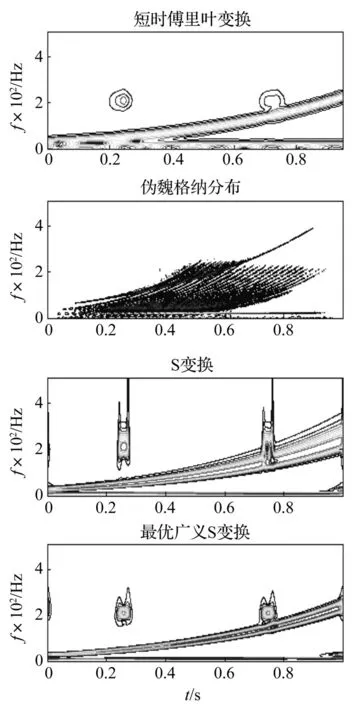
图2 仿真信号的时频图Fig.2 Time-frequency images of the simulated signal

2 基于脉冲耦合神经网络的时频图特征提取

2.1 脉冲耦合神经网络

最初的PCNN模型由Eckhorn提取，但该模型结构复杂，不便于应用。为此，本文选择文献[12]提出一种简化PCNN模型。该模型由信号接收部分、内部调制部分和脉冲发生器三部分组成，如图3所示。

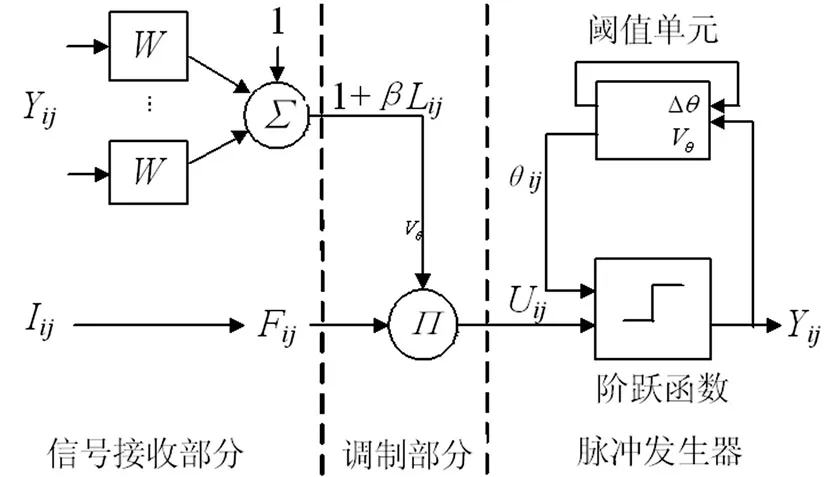
图3 简化PCNN神经元模型Fig.3 The neuron model of simplified PCNN

该简化PCNN模型可以由式(8)～(12)来描述：

Fij[n]=Iij

(8)

(9)

Uij[n]=Fij[n](1+βLij[n])

(10)

(11)

θij[n]=θij[n-1]-Δθ

(12)

其中:n为迭代次数；Fij、Iij、Lij、Uij、Yij和θij分别是神经元(i,j)的外部输入、外部激励、连接输入、内部活动项、脉冲输出和动态阈值；Δθ是θij的衰减步长；Yijkl为以神经元(i,j)为中心的局部脉冲输出；Wkl为连接权矩阵W的第(k,l)个元素；β为网络的耦合连接强度。

当β≠0时，PCNN存在局部耦合，PCNN利用耦合连接输入Lij对反馈输入Fij进行非线性调制，使各神经元之间相互影响，导致一个神经元发放脉冲的同时，会捕获其邻域内与之相似的神经元也发放脉冲，出现脉冲同步发放的现象。

2.2 最优广义S变换时频图特征提取

轴承故障信号经最优广义S变换后得到一个二维时频图，本文利用简化PCNN良好的脉冲同步发放特性，对时频图进行二值分解，然后提取用于描述轴承故障信号的特征参数。

利用PCNN对时频图二值分解时，对时频图进行归一化处理，使其元素在0～1，然后以归一化时频图的各元素作为PCNN神经元的外部激励。由于PCNN捕获神经元是自上而下的，外部激励较大的神经元将首先点火。随着迭代次数的增加，动态阈值呈线衰减，所有神经元都会依次发放脉冲，从而得到一个二值图像序列。此二值图像序列包含了时频图全部信息。

基于二值图像序列，借鉴灰度图像颜色直方图的概念，定义图像像素的捕获比，将时频图的二值图像序列转化为一维时间序列R[n]。图像像素的捕获比定义为每次迭代新捕获神经元个数与二值图像像素总数的比值，即：

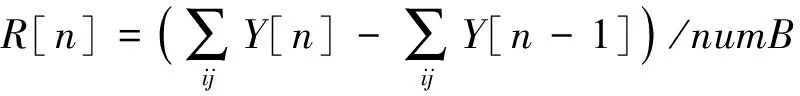
(13)

其中:numB表示二值图像的像素总数。

由于PCNN具有脉冲同步发放特性，并且神经元点火时刻能够大致反映出神经元对应时频图元素的大小，因而捕获比序列R[n]能够反映出轴承故障信号在时频面内的能量分布情况和局部结构信息。据此，本文提取捕获比序列作为轴承故障信号的特征参数。

3 滚动轴承故障信号分析

3.1 滚动轴承信号描述

本研究所采用的滚动轴承振动信号来自一个单级传动齿轮箱振动实验。实验中采用的轴承型号为SKF6205深沟球轴承，并通过电火花机分别在轴承外圈、内圈和滚动体上加工故障直径为0.053 mm的凹槽来模拟轴承外圈故障、内圈故障和滚动体故障。在载荷为3 hp的条件下，对每种轴承状态进行实验和采集数据，信号采样频率为12 kHz。本文对4种轴承信号进行分析，每种状态分别选取40个样本，样本长度为2 048个点。图4为滚动轴承4种状态下信号的时域波形。

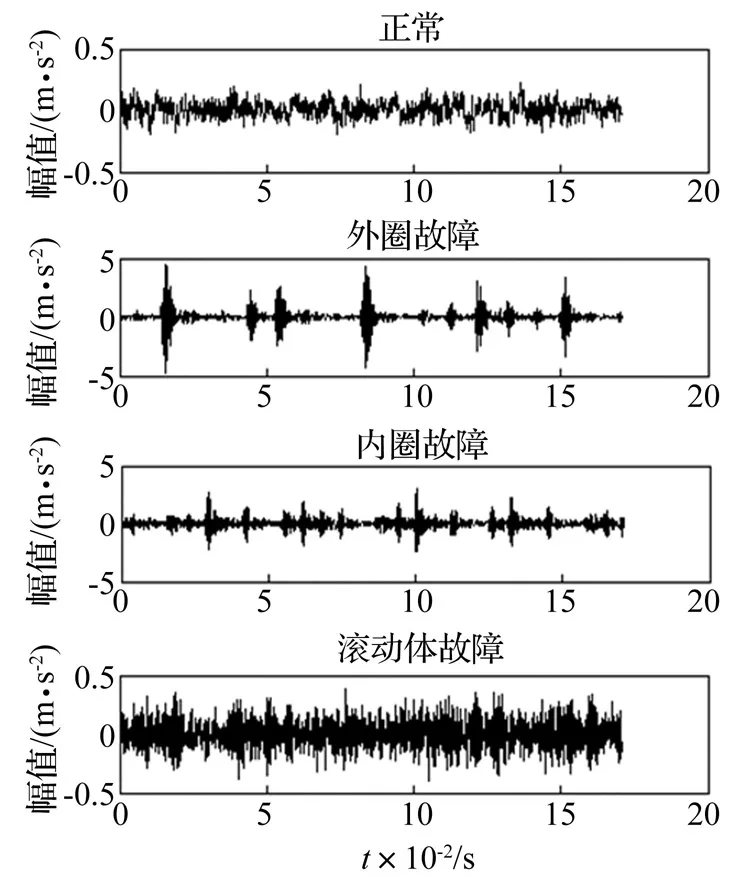
图4 轴承信号时域波形Fig.4 Time-domain waveforms of bearing signals

图5 正常信号时频图Fig.5 Time-frequency images of the normal signal

3.2 轴承故障信号时频表示

为了对比最优广义S变换在轴承信号时频表示中的优势，对图4中4种状态信号分别采用短时傅里叶变换、伪魏格纳分布、S变换和最优广义S变换进行分析，结果如图5～8所示。

通过对比4幅图可以看出，由于短时傅里叶变换高斯窗口宽度固定，不能在时域和频域同时取得较高的分辨率，因此时频聚集性较差；因为轴承信号常常是由多个分量信号组成的，所以伪维格纳分布时频图中不可避免出现交叉项，严重影响图像的辨识，其中正常和滚动体故障信号尤为明显；对于轴承外圈和内圈故障信号而言，S变换的时频聚集性优于短时傅里叶变换、伪魏格纳分布，但是对于正常和滚动体故障信号而言，其时频聚集较差，尤其是2 000 Hz以上频率成分；最优广义S变换能够根据信号自身的特点，自适应选择广义S变换中调整参数p的大小，因此4种轴承信号的最优广义S变换时频图的时频聚集性都比较好。因此，最优广义S变换更加适合于处理非平稳轴承故障信号。

图6 外圈故障信号时频图Fig.6 Time-frequency images of outer race fault signal

图7 内圈故障信号时频图Fig.7 Time-frequency images of inner race fault signal

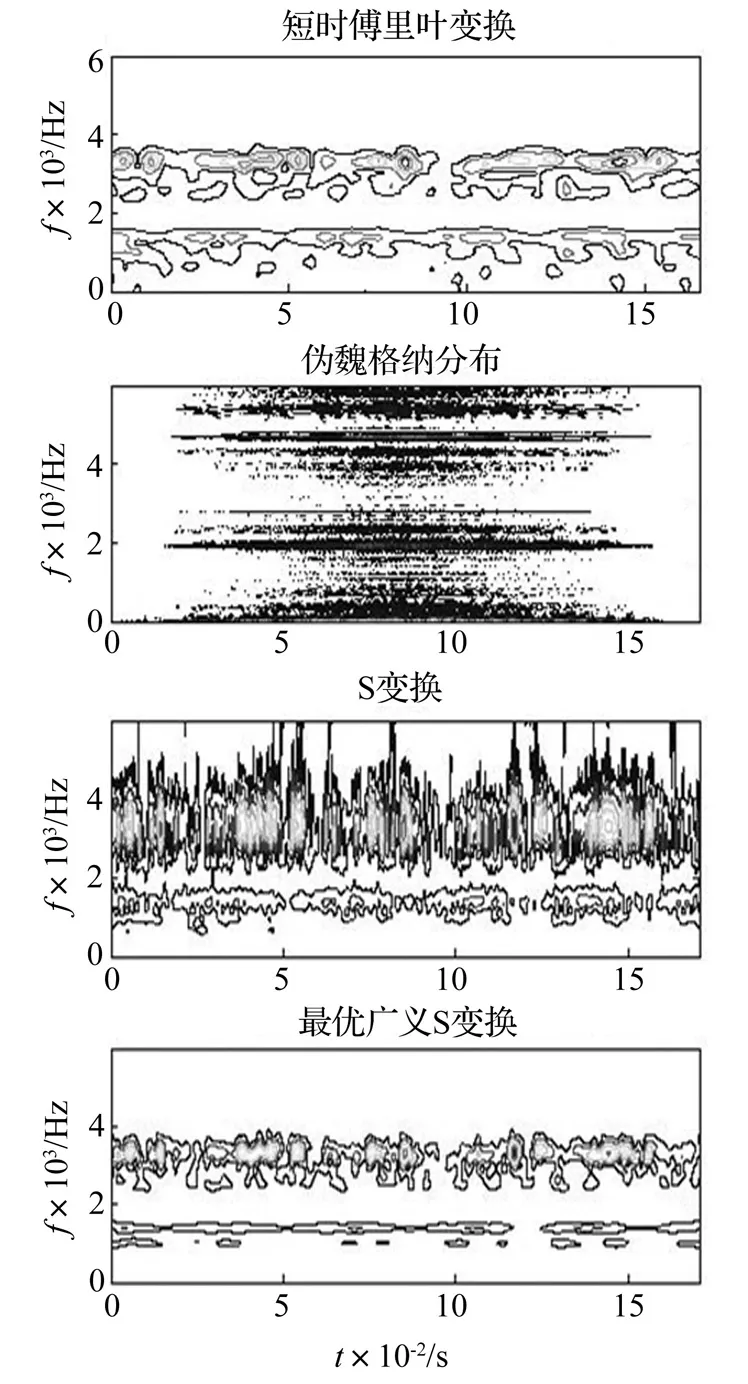
图8 滚动体故障信号时频图Fig.8 Time-frequency images of ball fault signal

3.3 脉冲耦合神经网络特征提取

在提取特征时，需要先对简化PCNN模型参数进行设置。简化PCNN模型涉及4个参数Wkl、β、Vθ和Δθ，其中Vθ为动态门限θij的初值。Wkl的取值比较固定，一般选为[0.661,1,0.661;1,1,1; 0.661,1,0.661]，其余参数主要通过经验和具体对象进行设置。经多次实验，β=0.1时提取的特征区分性能较好，故选取β=0.1；由于归一化时频图中最大元素为1，因此设置Vθ=1；为了兼顾描述能力和时间消耗，选择衰减步长Δθ=0.05。这样PCNN将从每个时频图中提取20个特征用于描述轴承信号。

图9给出了4种轴承信号的特征提取结果，其中每类状态包含5个样本。图9(a)为短时傅里叶变换提取结果，所有曲线分布杂乱，从图中很难准确区分轴承的4种不同状态，原因在于STFT不能自适应调整高斯窗口大小，时频图时频聚集性较差；图9(b)是伪魏格纳分布时频图提取结果，由于WVP存在交叉项，时频分布比较模糊，致使提取的特征参数区分性能较差；S变换克服了短时傅里叶变换的缺点，并且不存在交叉项，时频聚集性得到提高，基于S变换提取的特征如图9(c)所示，特征参数的类聚性明显好于STFT和WVP，但是类间分散性不是很理想；最优广义S变换通过对调整参数p的寻优，进一步提高了时频图的时频聚集性，基于最优广义S变换的特征提取结果如图9(d)所示，从图中可以看出捕获比序列不仅表现出良好的类聚性，而且类间分散性也比较理想。特征提取结果表明，最优广义S变换由于具有良好时频聚集性，更加适合于构造时频图，用于提取轴承信号特征参数。

图9 轴承信号特征提取结果Fig.9 Feature extraction results of bearing signals

3.4 轴承故障信号分类

为进一步验证基于最优广义S变换和简化PCNN模型所提特征的优越性，从每类信号中随机选取20个样本作为训练样本，其余20个样本作为测试样本，分别采用k-近邻分类器(k-NNC)、朴素贝叶斯分类器(NBC)和支持向量分类器(SVC)对轴承故障进行识别。在k-NNC分类时，取k=5；在SVC分类时，采用径向基核函数和“一对一”策略构建多类分类器，并通过交叉验证的方法自动选择参数。

实验分类结果如表1所示，其中STFT、WVP、ST和GST分别表示短时傅里叶变换、伪魏格纳分布、S变换和广义S变换。从表1可以看出，无论选择何种分类器，WVP的分类效果最差，其次是STFT，采用SVC分类时，ST和最优GST具有相同的分类精度，而采用k-NNC和NBC分类时，最优GST分类精度比ST高。总体而言，最优GST分类效果优于STFT、WVP和ST。

表1 轴承信号分类精度(%)

4 结 论

针对非线性、非平稳滚动轴承故障信号，设计了基于能量聚集性最优化的广义S变换，并与脉冲耦合神经网络结合，提出了一种基于最优广义S变换和脉冲耦合神经网络的故障特征提取方法。利用简化脉冲耦合神经网络良好的脉冲同步发放特性对最优广义S变换时频图进行二值分解，定义和提取二值图像的捕获比序列，以此作为滚动轴承故障信号的特征参数。仿真信号和轴承故障信号分析结果表明，与S变换、短时傅里叶变换和伪魏格纳分布相比，最优广义S变换具有更好的时频聚集性，基于广义S变换和脉冲耦合神经网络提取的特征参数具有最高的识别精度，更加适用于轴承故障诊断。

[1] 李辉, 郑海起, 唐立伟. 基于双树复小波包峭度图的轴承故障诊断研究[J]. 振动与冲击, 2012, 31(10): 13-18. LI Hui, ZHENG Hai-qi, TANG Li-wei. De-noising method based on generalized morphological component analysis[J]. Journal of Vibration and Shock, 2012, 31(10): 13-18.

[2] 丁康, 李巍华, 朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京: 机械工业出版社, 2005.

[3] 迟华山, 王红星, 郭奇, 等. 短时傅里叶变换在线性调频信号时频滤波中的应用[J]. 电讯技术, 2012, 52(2): 155-159. CHI Hua-shan, WANG Hong-xing, GUO Qi, et al. Application of STFT in time-frequency filtering of LFM signals[J]. Telecommunication Engineering, 2012, 52(2): 155-159.

[4] 蔡艳平, 李艾华, 石林锁, 等. 基于EMD-WVD振动谱时频图像SVM识别的内燃机故障诊断[J]. 内燃机工程, 2012, 33(2): 72-79. CAI Yan-ping, LI Ai-hua, SHI Lin-suo, et al. IC engine fault diagnosis method based on EMD-WVD vibration spectrum time-frequency image recognition by SVM[J]. Chinese Internal Combustion Engine Engineering, 2012, 33(2): 72-79.

[5] Saravanan N, Kumar Siddabattuni V N S, Ramachandran K I. A comparative study on classification of features by SVM and PSVM extracted using Morlet wavelet for fault diagnosis of spur bevel gear box[J]. Expert Systems with Applications, 2008(35): 1351-1366.

[6] Stockwell R, Mansinha L, Lowe R.Localization of the complex spectrum: The S-transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[7] Djurovi I, Sejdi E, Jiang J. Frequency-based window width optimization for S-transform,[J]. AEU-International Journal of Electronics and Communications, 2008, 62(4): 245-250.

[8] 郑旭, 郝志勇, 金阳, 等. 自适应广义S变换在内燃机气缸盖振动特性研究中的应用[J]. 振动与冲击, 2011, 30(1): 167-170. ZHENG Xu, HAO Zhi-yong, JIN Yang,et al. Application of adaptive generalized S-transform in vibration characteristics analysis of an IC engine cylinder head [J]. Journal of Vibration and Shock, 2011, 30(1): 167-170.

[9] GU Xiao-dong. Feature extraction using unit-linking pulse coupled neural network and its applications[J]. Neural Process Letter, 2008(27): 25-41.

[10] MA Yi-de, LIU Li, ZHAN Kun, et al. Pulse coupled neural networks and one-class support vector machines for geometry invariant texture retrieval[J].Image and Vision Computing, 2010(28): 1524-1529.

[11] 陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J]. 信号处理, 2008, 24(1): 28-31. CHEN Xue-hua, HE Zhen-hua, HUANG De-ji. Generalized S transform and its time-frequency filtering[J]. Signal Processing, 2008, 24(1): 28-31.

[12] 张云强, 张培林, 任国全. 简化PCNN在磨粒图像颜色特征提取中的应用[J]. 内燃机工程, 2013, 34(5): 69-75. ZHANG Yun-qiang, ZHANG Pei-lin, REN Guo-quan. Application of simplified PCNN in color feature extraction for wear particle images[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(5): 69-75.

Bearing fault diagnosis based on optimal generalized S transform and pulse coupled neural network

ZHANG Yun-qiang, ZHANG Pei-lin, WU Ding-hai, LI Bing

(Department of Vehicles and Electrical Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

Aiming at the nonlinear and non-stationary characteristics of rolling bearing fault signals, a feature extraction method based on optimal generalized S transform and pulse coupled neural network(PCNN) was proposed. The generalized S transform was optimized by measuring the time-frequency aggregation, and then utilized to achieve time-frequency representations of bearing fault signals. Time-frequency images were further decomposed into a series of binary images by the PCNN. The capture rate sequences of binary images were then defined and extracted as the bearing fault feature parameters. The rolling bearing signals under four different states were analyzed. The results indicate that the proposed method can extract more effective bearing fault feature parameters which are capable of improving the bearing fault diagnosis accuracy.

fault diagnosis; rolling bearing; feature extraction; generalized S transform; pulse coupled neural network(PCNN)

国家自然科学基金资助项目(E51205405,51305454)

2013-11-01

张云强 男，博士生，1987年9月生

张培林 男，教授，博士生导师，1955年12月生

TN911.72；TH133.33

A

10.13465/j.cnki.jvs.2015.09.005