考虑易损件物品-EPE缓冲系统冲击响应分析
2015-03-17卢富德
张 炜, 薛 飞, 卢富德, 高 德
(1.浙江大学 宁波理工学院,浙江 宁波 315100; 2.太原科技大学,太原 030024)
考虑易损件物品-EPE缓冲系统冲击响应分析
张 炜1, 薛 飞2, 卢富德1, 高 德1
(1.浙江大学 宁波理工学院,浙江 宁波 315100; 2.太原科技大学,太原 030024)
为研究易损件在发泡聚乙烯(EPE)缓冲作用下冲击响应,建立了二自由度非线性产品包装系统模型,分析了易损件与EPE黏弹性耦合后的跌落加速度特性,讨论破损边界上方区域内衬垫面积、厚度及其比值对易损件加速度响应的影响。结果表明,满足约束条件的易损件的最大加速度响应与缓冲衬垫面积和厚度关系成条状特性。随着EPE缓冲衬垫面积与厚度增大,易损件加速度先减小后增大。易损件最大响应加速度与缓冲衬垫体积关系呈现“√”形状,最后引入系数表征缓冲衬垫的经济性和易损件安全性。
易损件;跌落;EPE;缓冲;冲击
缓冲衬垫用于防止产品在运输过程中跌落冲击引起的产品破损[1-2],特别是关键易损件的损坏。但在进行缓冲设计与分析时,常常忽略易损件,或将易损件、产品、缓冲包装隔离考虑,忽略产品复杂结构因素及其对产品破损的影响以提升计算效率,但结果与实际情况有较大的误差[3]。王志伟等[4-5]采用归一化系统参数研究了半正弦波冲击对易损件破损边界的影响。王军等[6-7]研究了半正弦脉冲激励下考虑易损件的正切型包装系统冲击特性及正切型包装系统冲击破损边界曲面。Mills等[8-9]利用有限元方法研究了缓冲材料的应力-应变关系,预测复杂形状缓冲材料的性能。基于实验对包装材料缓冲特性进行研究,建立其本构模型,更便于在工程设计中进行缓冲优化设计[10-13],该方法可摒弃基于最大加速度—静应力曲线设计的弊端。高德等[14]基于跌落冲击实验建立了EPE的本构关系,建立其多自由度缓冲模型,研究对整个包装件的缓冲特性,但并未考虑含易损件的情况。
产品的破损往往首先出现在某个易损件[15],对易损件的缓冲保护往往是导致缓冲系统设计成败的关键。本文基于实验获得的EPE本构关系,将研究耦合线弹性易损件包装系统的缓冲特性,分析EPE的面积和厚度对缓冲特性的影响,并提出采用线性插值方法综合考虑缓冲衬垫经济性和安全性的参数。
1 易损件-EPE缓冲包装系统模型
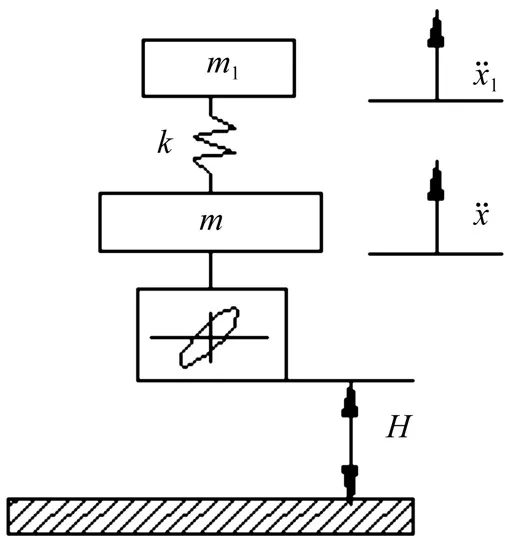
图1 EPE非线性跌落模型Fig.1 Nonlinear drop model of the EPE
本文考虑包含线弹性易损件的包装件在缓冲衬垫上,并随其一起跌落缓冲过程,其简图如图1所示。
其动力学方程为:
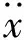
EPE材料跌落缓冲本构模型为[14]:
(2)
式中:a1=0.002 8 MPa/s,a2=395.36 Pa/s,a3=0.038 MPa,a4=0.089 4 MPa,a5=1.91 MPa/s。
得到EPE缓冲材料的弹性力为:
(3)
则方程(1)变为
(4)
从易损度角度进行缓冲包装设计时,需要同时考虑① 物品及易损件无量纲最大加速度小于易损度;② 衬垫尺寸的面积和厚度之比满足A≥(kh)2,通常k取1.33。
2 计算结果及分析
电子元器件常常仅重数克,采用上述模型试算之,上述模型中取包装物品质量m=5 kg,易损件质量m1=5 g,f=50 Hz,k=493.5 N/m,易损度Gm=80 g,跌落高度H=0.6 m。
采用式(4)计算跌落冲击过程中物品和易损件加速度,图2为加速度响应图。计算中假设在整个跌落过程,即从缓冲衬垫被压缩到最大至反弹到原始厚度过程中包装件和EPE缓冲衬垫都紧密接触不分离,并且缓冲衬垫恢复至原始厚度后,强制缓冲衬垫保持原始厚度不变,此时刻后,物品加速度为0,线弹性易损件则作简谐振动。这样,物品在缓冲过程中其加速度如图2所示为一个近似半正弦波,之后保持加速度为零;而易损件则完成一个近似完整的正弦波冲击过程后,立即进行简谐振动。此过程以图中AA线段为界限,这两个状态的转变过程在此刻突变,计算中忽略其变化过程。在图2中,线弹性易损件加速度峰值滞后于物品加速度峰值,这是由于易损件的固有频率较小,即如果其固有频率选择较大,其峰值将向左侧前移,其加速度正弦波个数可能会大于1,但AA线段右侧简谐振动趋势不变。
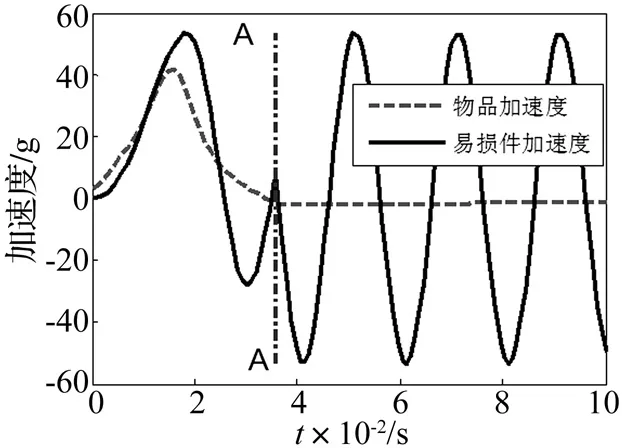
图2 物品和易损件加速度响应Fig.2 Acceleration response curve of a goods and a critical component
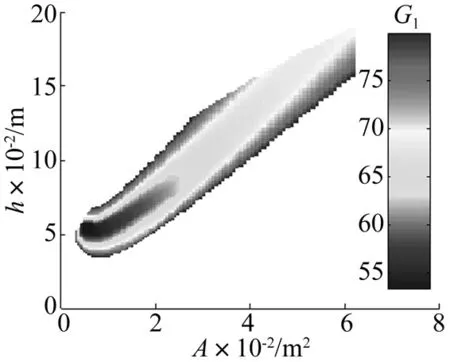
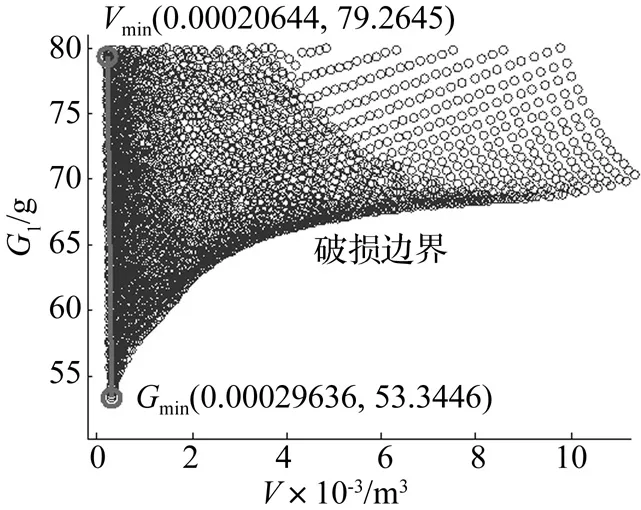
图3、4为易损件获得的无量纲最大加速度G1与EPE的面积A和厚度h的关系。图3为G1随缓冲衬垫面积A和厚度h变化的曲面图,图4为满足G1 由图3可见,EPE缓冲衬垫的面积A和厚度h对易损件的响应影响非常大,G1最大值出现在A和h均较小的区域,并且随A与h增大,整体呈快速下降趋势。但G1并不是随着A和h增大而单调减小,其最小值并没有出现在A和h值最大的边缘,这是由于易损件的线弹性和EPE的黏弹性两种效应叠加的效果。在大多数区域内,即使相同的缓冲衬垫面积A,G1也是随着厚度h增大呈现波动趋势。对于厚度h,情况也相似。 图3 易损件无量纲最大加速度图Fig.3 Dimensionless maximum acceleration graph of a critical component 图4为满足G1 图4 易损件无量纲最大加速度强度图Fig.4 Dimensionless maximum acceleration intensity graph of a critical component 图5 EPE体积对易损件加速度的影响Fig.5 EPE ’s volume effect on acceleration of a critical component 图5为易损件加速度G1与缓冲衬垫体积V的关系。对于线弹性易损件,存在明显的破损边界,呈现“√”形状。其上方数据点显示,即使具有相同体积的缓冲衬垫,由于A和h的组合不同,产生的加速度差异巨大。“√”左侧边界接近于V=0纵坐标,满足G1 V=Vmin-λ(Vmin-VG1min) (5) 本文基于EPE缓冲材料动态本构模型,建立了考虑产品的易损件情况下EPE缓冲包装冲击动力学方程。根据易损件在EPE衬垫作用下的冲击响应,分析了EPE衬垫的厚度和面积对易损件的影响。结果表明,小幅度的增加厚度或面积对易损件响应产生较大的影响,且使易损件响应小于易损度的EPE的面积和厚度成条状区域关系。综合考虑缓冲包装设计的经济性和安全性,引入系数λ,在破损边界区域利用线性插值方法平衡包装优化设计目标的权重,为缓冲包装设计提供有效的方法。 [1] Liu Y, Kessels F J H G, van Driel W D, et al. Comparing drop impact test method using strain gauge measurements[J]. Microelectronics Reliability, 2009, 49: 299-303. [2] Da Yu, Kwak J B, Park S, et al. Dynamic responses of PCB under product-level free drop impact[J]. Microelectronics Reliability, 2010, 50:1028-1038. [3] 王军,王志伟. 阻尼对正切型包装系统易损件冲击谱影响[J]. 振动与冲击, 2008, 27(9): 175-177. WANG Jun, WANG Zhi-wei. Effect of damping on three-dimensional shock spectra of a tangent packaging system with a critical component[J]. Journal of Vibration and Shock, 2008, 27(9): 175-177. [4] Wang Zhi-wei, Jiang Jiu-hong. Evaluation of product dropping damage based on key component[J]. Packaging Technology and Science, 2010, 23: 227-238. [5] Wang Jun, Jiang Jiu-hong, Lu Li-xin, et al. Dropping damage evaluation for a tangent nonlinear system with a critical component[J]. Computers and Mathematics with Applications, 2011, 61: 1979-1982. [6] 王军, 王志伟. 考虑易损件的正切型包装系统冲击破损边界曲面研究[J]. 振动与冲击,2008, 27(2):166-167. WANG Jun, WANG Zhi-wei. Damage boundary surface of a tangent nonlinear packaging system with critical component[J].Journal of Vibration and Shock, 2008, 27(2):166-167. [7] 王军, 王志伟. 半正弦脉冲激励下考虑易损件(关键部件)的正切型包装系统冲击特性研究[J]. 振动与冲击, 2008, 27(1):167-168. WANG Jun, WANG Zhi-wei. 3-Dimensional shock response spectra charaterizing shock respone[J]. Journal of Vibration and Shock, 2008, 27(1):167-168. [8] Mills N J, Masso-Moreu Y. Finite element analysis (FEA) applied to polyethylene foam cushions in package drop tests[J]. Packaging Technology and Science, 2005, 18: 29-38. [9] Mills N J, Stampfli R, Maronec F,et al. Finite element micromechanics model of impact compression of closed-cell polymer foams[J]. International Journal of Solids and Structures, 2009, 46: 677-697. [10] 卢富德, 高德. C楞瓦楞纸板动态缓冲模型及应用[J]. 功能材料, 2012, 43(1): 39-41. LU Fu-de, GAO De. Cushion model and its application of c-flute corrugated paperboard[J]. Journal of Functional Materials, 2012, 43(1): 39-41. [11] 卢富德, 陶伟明,高德. 串联缓冲系统冲击响应与结构优化分析[J]. 浙江大学学报(工学版),2012,46(10): 1773-1777. LU Fu-de, TAO Wei-ming, GAO De. Impact response of series cushionging system and structure optimization analysis[J]. Journal of Zhejiang University(Engineering Science),2012, 46(10): 1773-1777. [12] 卢富德, 陶伟明,高德. 瓦楞纸板串联缓冲系统动力学响应[J]. 振动与冲击, 2012, 31(21): 30-32. LU Fu-de, TAO Wei-ming, GAO De. Dynamic response of a series cushioning packaging system made of multi-layer corrugated paperboard[J]. Journal of Vibration and Shock, 2012, 31(21): 30-32. [13] 卢富德, 高德.考虑蜂窝纸板箱缓冲作用的产品包装系统跌落冲击研究[J]. 振动工程学报,2012,25(3):335-341. LU Fu-de, GAO De. Study on drop impact of packaging system considering the cushioning action of honeycomb paperboard box[J]. Journal of Vibration Engineering, 2012,25(3):335-341. [14] 高德, 卢富德. 聚乙烯缓冲材料多自由度跌落包装系统优化设计[J]. 振动与冲击,2012, 31(3): 69-72. GAO De, LU Fu-de. Optimization design of MDOF package cushioning system made of polyethylene[J]. Journal of Vibration and Shock, 2012, 31(3): 69-72. [15] Wang Jun, Duan Fang, Jiang Jiu-hong, et al. Dropping damage evaluation for a hyperbolic tangent cushioning system with a critical component[J]. Journal of Vibration and Control, 2011,18: 1417-1421. Impact-response analysis of the system composed of critical component and EPE cushion ZHANG Wei1, XUE Fei2, LU Fu-de1, GAO De1 (1. Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China;2. Taiyuan University of Science and Technology, Taiyuan 030024, China) In order to investigate the impact response of cushioning systems made of expanded polyethylene (EPE)and items with critical component, a nonlinear packaging model with two degrees of freedom containing a critical component was established, and solved by using numerical method with a given constitutive relationship of EPE. The impact response in terms of acceleration histories of the cushioning system was obtained, and the effects of cushion area, height and their ratio on the acceleration distribution on damaged boundary were discussed. The numerical results show that the acceleration response of the critical component is influenced appreciably by the above parameters. It is shown that the relationship between the maximum acceleration response of the critical component and the area and thickness of the cushion appears a strip shape character when the cmponent meets the fragility requirements and dimension requirements. As the area and thickness of EPE cushion increase, the acceleration decreases first and then increases. The relationship between the acceleration and the volume of EPE cushion is like the symbol “√”. At last, a parameter was introduced to describe the cushion economy and the critical component safety. critical component; drop; EPE; cushion; impact 国家自然科学基金(11402232);宁波市自然科学基金(2011A610154);国家十二五重大科技支撑项目(2011BAD24B01) 2014-01-27 修改稿收到日期:2014-05-06 张炜 男,副教授,1975年生 邮箱:zhweiyuan@163.com TB485.3;O322 A 10.13465/j.cnki.jvs.2015.09.021
G1=G1Vmin-λ(G1Vmin-G1G1min)3 结 论
