高超声速助推-滑翔式飞行器中段弹道轨迹分析

徐申达，吴 京，王雪莹

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

高超声速助推-滑翔式飞行器中段弹道轨迹分析

徐申达，吴 京，王雪莹

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

提出了一种高超声速助推-滑翔式飞行器中段弹道轨迹设计方法，并对弹道特性进行了仿真。首先介绍了高超声速助推-滑翔式飞行器的概念和它的基本弹道轨迹，分析了传统轨迹设计中的不足。然后提出了一种机动程序和发动机短暂点火相结合控制跃起，综合考虑实时精确的空气动力、地球引力以实现跳跃式飞行的弹道轨迹设计方法，并在机动控制程序不变时对点火次数、点火高度和推力大小进行了弹道仿真分析。仿真结果显示了该方法的可行性、整体设计上的优势以及在增大射程、提高突防能力上的性能优势。

高超声速助推-滑翔式飞行器；弹道轨迹；机动控制程序；弹道仿真

0 引言

近年来，突防技术作为弹道导弹提高生命力的重要措施，已成为军事强国新一代弹道导弹的基本设计要素。滑翔式机动弹头是近十年来美、俄积极发展的弹头新技术，采用该技术可使弹道导弹增强突防能力，是未来弹头技术发展的新方向。20世纪30年代，德国科学家Saenger 提出了一种不断跳跃进出大气层的名为“银鸟”的“助推-跳跃滑翔”飞行器[1]；1948年，钱学森教授在美国火箭学会年会上提出了一种在主动段用运载火箭进行助推，再入大气层后无动力滑翔飞行，最终可完成洲际飞行的飞行器。美国目前研究的“高超声速技术飞行器”(HTV)，其常规打击导弹的载荷运送装置也是一种无动力的高超声速滑翔飞行器。国内也基于“钱学森弹道”提出了几种新概念飞航导弹[2]的构思。

其中高超声速助推-滑翔式飞行器(HBG)主要是把火箭助推与高超声速滑翔技术相结合，采用与传统洲际导弹完全不同的弹道，形成具有极高突防能力的全球常规快速打击武器，成为美、俄近年来大力发展的目标。据报道，俄罗斯已完成此项技术研究，并成功进行了飞行试验，这将成为俄罗斯未来对付美国导弹防御系统装备的重要战略武器之一。本文正是基于HBG的构想，结合工程实际，在弹道中段采用攻角机动程序控制和发动机短暂点火相结合，综合考虑空气动力、地球引力等，提出一种高超声速助推-滑翔式飞行器中段弹道轨迹设计方法，实现飞行器再入大气层后跳跃式飞行，获得较远的射程。

1 高超声速助推-滑翔式飞行器基本弹道轨迹

根据美国公开的高超声速飞行器资料[3]，综合考虑作战性能实际，HBG弹道可分为主动段、中段、末段，而它与弹道导弹不同之处即在于中段，可分为自由飞行段和跳跃滑翔段。在主动段通过运载火箭助推，压低弹道高度，避开导弹防御系统监测；发动机关机后，机动弹头以较小倾角释放，再入大气层后，利用高升阻比的气动外形，经过攻角机动程序控制或者发动机短暂点火，实现在大气层内的跳跃飞行；在末段，飞行器靠近目标时利用末段制导击中目标。基本弹道如图1所示。由于中段飞行段是HBG与其它弹道的区别所在，因此本文主要研究HBG的中段弹道轨迹。

图1 HBG基本弹道

2 高超声速助推-滑翔式飞行器弹道轨迹设计方法

传统HBG的弹道轨迹设计，在弹体从波谷到波峰的跃起过程中，通常采用的是发动机短暂点火或者添加攻角机动程序[4]，实现跳跃式飞行。同时空气动力和地球引力采用固定值，不能精确地模拟HBG飞行过程中情况。HBG飞行高度高，一般为20～100km，设计的最大Ma数可达20以上，因此突防能力极强。由于HBG飞行速度较高，基于工程实际和仿真分析，在实现跳跃飞行时单纯靠改变攻角并不能完全保证弹体飞行状态的改变，因此，本文采用发动机短暂点火和攻角机动程序相配合的方式，确保实现弹体再入大气层后的跳跃飞行，并可通过更改参数实现最大射程。同时空气动力使用实时参数，地球引力采用准确的平方反比模型，最佳地模拟HBG的飞行状态。对其进行受力分析，如图2所示。

图2 HBG受力情况分析

1)地球引力

飞行器在飞行过程中全程受到地球引力的作用[5]：

Gx=mgcosγ

Gy=mgsinγ

(1)

式中，m为飞行器的质量，飞行器在飞行过程中，质量会随着燃料的消耗及飞行器高温热损耗而减小。由于质量的变化较复杂，需要考虑的问题较多，而本文研究飞行器在弹道中段的轨迹，飞行器除了发动机短暂点火外质量消耗极小，为简化分析忽略不计。

极坐标角γ可通过下式计算：

tanγ=x/(R+y)

(2)

式中，x、y分别为飞行器在发射坐标系中的坐标。

地球引力模型采用平方反比模型，即重力加速度为：

g=0.0098(R/r)2

(3)

采用实时变化的重力加速度，提高了计算精度。

2)空气动力

飞行器在飞行过程中全程受到空气动力影响。空气动力分为空气阻力和空气升力。x、y分别是飞行器在发射坐标系下的坐标。

Fx=-Lcosβ-Dsinβ

Fy=-Lsinβ+Dcosβ

(4)

式中，Fx、Fy分为x、y方向上的气动力，L为空气阻力，D为空气升力。飞行器在飞行过程中的空气动力由飞行器速度V、大气密度、特征面积SM等决定，且阻力和升力的关系由阻比L/D确定，空气阻力与升力可通过下式计算[5]：

①空气阻力

L=ρV2CxSM/2

(5)

②空气升力

D=ρV2CySM/2

(6)

式中，Cx为飞行器阻力系数，Cy为飞行器升力系数，受到飞行器形状的影响[6]。

在飞行过程中，飞行器的空气动力受到速度、结构和大气密度的影响，而大气密度是随着飞行器的高度而实时变化的，在弹道分析计算中，若将标准大气表中的上万个数据输入计算机，工作量及存储量是很大的。因此，本文使用的大气模型采用《远程火箭动力学》里的拟合公式[6]，该拟合公式是以标准大气表为依据，采用拟合法得出的从海平面到91km范围内的标准大气参数计算公式。其计算精度足够，可替代大气标准表。

3)发动机推力

在飞行器从大气外部飞入大气层时开始补偿动力，即开始进行点火机动，改变姿态并逐渐上升。飞行器在重新飞出大气层后停止加速。在飞行高度低于设定点火高度时发动机短暂点火给予推力。在给予推力过程中，假设推力是均匀稳定的，同时弹体质量减少忽略不计。

Px=Pcosα

Py=Psinα

(7)

式中，俯仰角α为攻角a(t)与速度向量V对发射点水平线的夹角β之和[7]，飞行器为达到机动的目的，一般采用攻角机动控制程序实现，而本文中对于HBG飞行器，为了保证飞行器能正确跃起以及精确控制飞行器跃起时的姿态，采用发动机短暂点火和攻角α采用机动控制程序相结合的方式来实现飞行器的跳跃机动，即：

α=β+a(t)

(8)

文献[8]中将飞行器飞行过程分为三个阶段，第一阶段为发动机点火后，弹体爬升至发动机关机，此阶段弹道类似弹道导弹“抛物线”状；第二阶段为再入大气层之后，弹头不是直接攻击目标，而是通过调整攻角使其俯冲后利用气动力再度升起；第三阶段是在大气阻力下，弹道轨迹会趋于平缓，为了提高弹头的杀伤力，需要在二次再入时调整攻角，使弹头低空俯冲落地时倾角大于70°，速度Ma数不低于1。本文中，将此过程适用于HBG，同时对此攻角程序进行改进，为了实现更大射程，将阶段提升至5个，实现弹体在大气层内的跳跃飞行，且阶段数可按射程需要实时调整。

研究发现，采用平稳的控制程序，可以实现飞行器的机动飞行。本文采用传统弹道常使用的一种攻角控制程序[9]，并对其进行改进。原始程序如下：

a(t)=-4amiZ(1-Z)

(9)

式中，Z=e-ai(t-ti)，i=1,2,3。设计值ami为基于工程实际允许的最大攻角，ai为常数，ai值的大小表征了转弯的快慢，增加ai值，转弯加快，减小ai值，转弯减慢；ti为第i阶段程序的起控时间。这种程序的优点是全程变化较为平缓，工程上易于实现，方便进行控制系统设计，同时可保证每阶段飞行器运动方程式不变，只需控制起控时间和ami、ai即可控制弹道。在弹道的前两个阶段采用式(9)的参数，在第三个阶段采用式(9)的相反数。改进时将i的值设为1,2,3,4,5，同时根据弹道初始情况修改各参数，具体参数见仿真分析。

3 仿真分析

采用美国波音公司设计的带控制翼的锥形体再入机动飞行器的相关气动参数进行优化[10]，其中最大升力系数为0.6,气动参考面积为0.35m2, 质量为907kg。弹道从中段开始，起始高度设为200km，即起始坐标为(0,200)。速度Ma数为20，即6.8km/s，最大法向过载不超过10g，弹道开始时弹体与发射点水平面夹角设为5°，升阻比L/D设为1，点火高度为30km，即在弹体低于30km时发动机点火，再次升起即高于30km时停止推力，推力大小为120000N，本文设计点火四次。攻角程序各参数值按照想要实现的弹道轨迹设计，具体参数值如表1所示。仿真结果如图3所示。

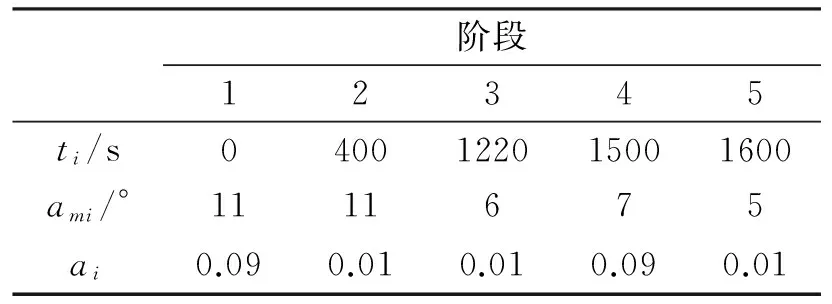
表1 攻角程序参数设计

图3 HBG弹道轨迹仿真结果

在整个飞行过程中，HBG从200km高空进入自由飞行段，在263.8s到达第一个最高点278.41km，此后再入大气层，在发动机点火推力和攻角改变的双重控制下，弹体在进入波谷后再次升起，实现跳跃飞行，在981.7s时达到第二个最高点154.43km，此后弹体运动到波谷时在控制下，再次升起，在1355.5s时到达第三个最高点72.70km，此后弹体继续运动到波谷时在控制下升起，在1579.9s到达第四个最高点43.01km，此后弹体在附加的俯冲程序下，满足弹体攻击前的姿态要求，利于打击目标。

本文算例设计的攻角变化趋势和文献[8]中设计的攻角变化对比如图4所示，可以看出，本文设计的攻角变化更加平缓，更有利于工程实现。

图4 本文算例和文献[8]攻角角度变化对比图

由于本文算例的弹道轨迹仿真结果在相同攻角程序控制下与点火次数、点火高度和推力大小有关，因此，需要对此进行仿真分析，以达到最优效果。

1)点火次数对射程的影响

在其余初始条件不变的情况下，设置点火次数如表2所示。

表2 点火次数对射程的影响

与弹道导弹相比，点火次数的增加可提高导弹突防能力。分析图5可知，在其余初始条件不变的情况下，随着点火次数的增加，弹体跳跃段的个数不断增加，射程也就不断增大，随着到达预定的攻角机动程序跳跃次数，射程会稳定在一个范围内，此时增加点火次数，射程不会有明显变化，甚至可能减小。说明发动机点火和机动程序控制缺一不可，二者相互配合才能实现最大射程的最优弹道。

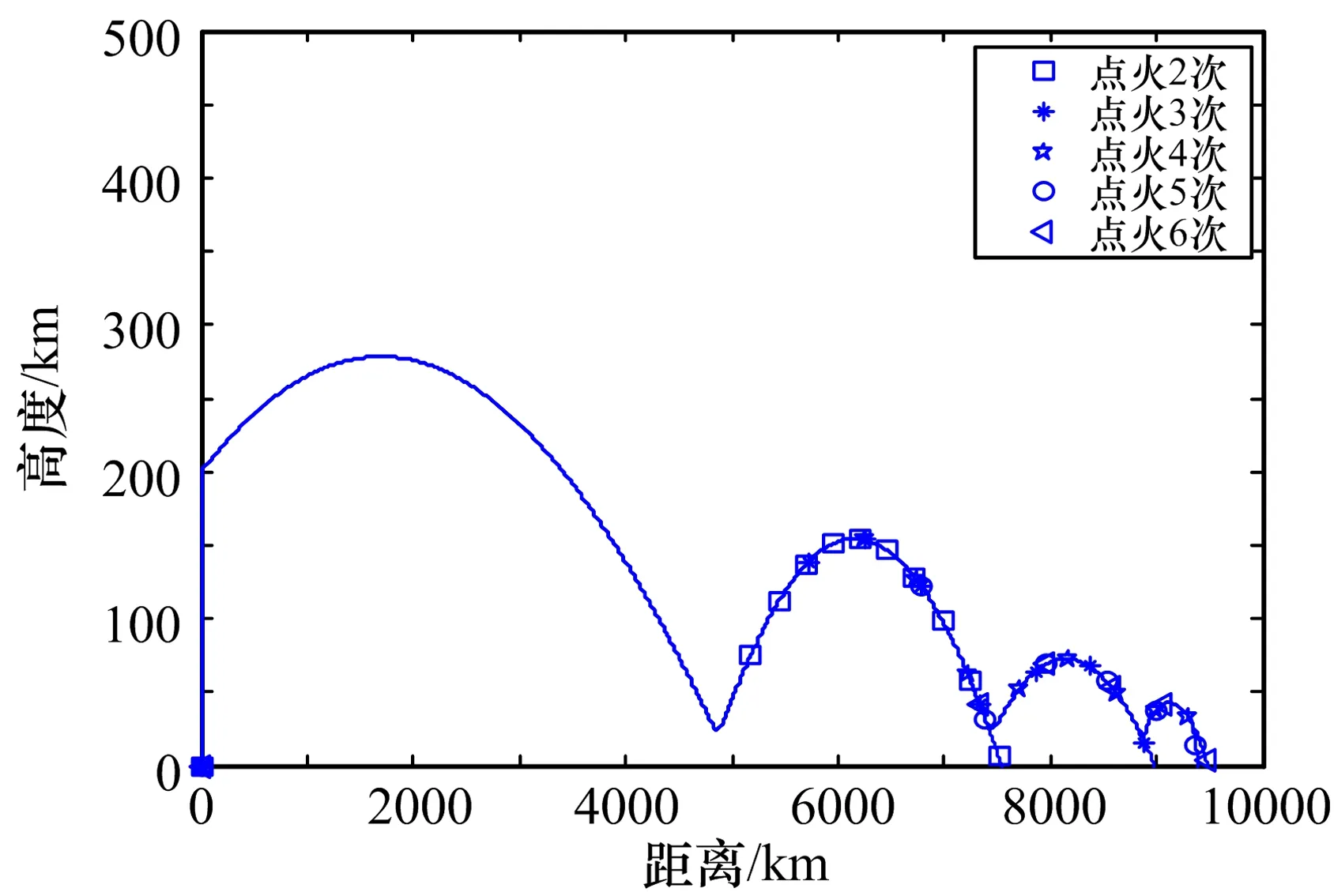
图5 点火次数对射程的影响

2)点火高度对弹道轨迹影响

在其余初始条件不变的情况下，设置点火高度如表3所示。

表3 点火高度对弹道轨迹影响

图6 点火高度对弹道轨迹影响

由仿真图6可知，在其余初始条件不变的情况下，点火高度发生改变对弹道轨迹影响较大。对第二次点火后跃起高度进行分析，在点火高度较低时，此时发动机点火提供推力已经不能够较大地改变弹体运动状态，使其再次跃起成跳跃弹道；在点火高度较高时，此时发动机点火提供推力足够对弹体的运动状态进行改变，使其再次跃起成跳跃弹道，但由于弹体跃起高度较高，超出了HBG的弹道范围，同时会产生较大的气动热量，不是理想弹道。在本次仿真中，只有当点火高度为30km左右时，才能得到理想弹道轨迹。

3)推力大小对弹道轨迹影响

在其余初始条件不变的情况下，设置推力大小如表4所示。

表4 推力大小对弹道轨迹影响

由仿真图7可知，在其余初始条件不变的情况下，改变点火时发动机推力的大小，对弹道轨迹的影响较大。通过对第二次点火后弹体跃起高度分析可知，推力较小时，在第二次发动机点火后弹体难以跃起实现跳跃式弹道；推力较大时，在第二次发动机点火后弹体跃起高度较高，超出了HBG的弹体机动范围，同时会产生较大的气动热量，不是理想弹道轨迹；在本次仿真中，只有当推力在120000N附近时，才能得到理想弹道轨迹。

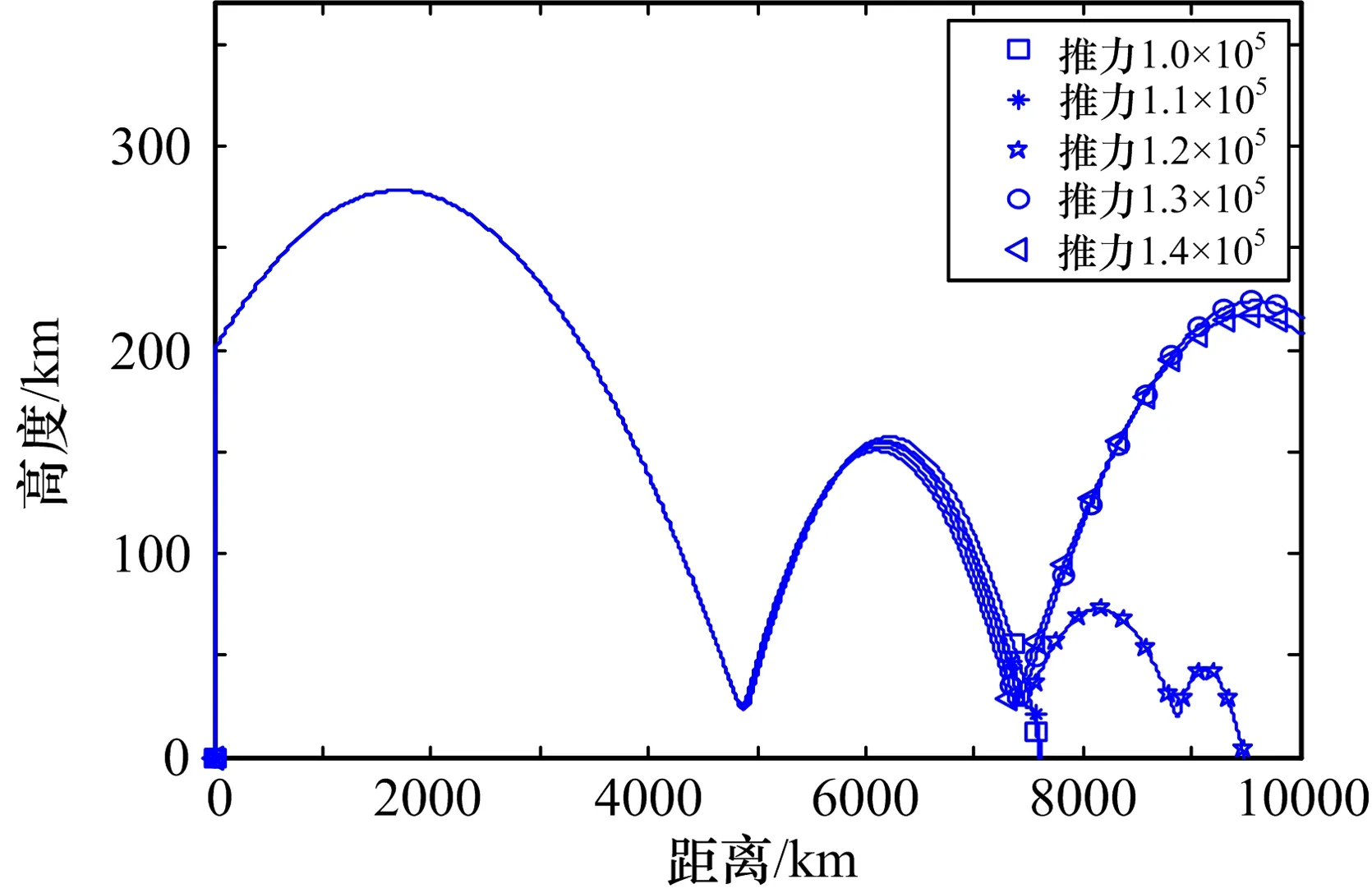
图7 推力大小对弹道轨迹影响

综合仿真结果可以看出，在攻角程序给定的情况下，点火次数对射程影响较大，而点火高度和推力大小则对弹体能否在波谷处成功跃起实现跳跃式飞行有较大影响。同时，点火次数、点火高度和推力大小与机动程序联系较紧密，在给定机动程序下，若要实现跳跃式飞行的弹道仿真结果，参数变化较为固定，有利于对高超声速助推-滑翔式飞行器进行整体设计。

4 结束语

本文结合工程实际，考虑环境等因素，提出一种采用发动机短暂点火和攻角程序控制相结合，综合考虑实时精确的空气动力和地球引力的高超声速助推-滑翔式飞行器弹道轨迹实现方法。该方法在实现HBG跳跃飞行时，可控性更强，能够精确控制弹体的跃起，实现跳跃式飞行，获得较远的射程，显示了该方法的可行性和在增大射程、提高突防能力上的性能优势。同时在仿真分析中也可看出，在攻角控制程序给定的情况下，点火次数、点火高度及推力大小可变范围较小，即攻角控制程序和发动机短暂点火的各影响参数匹配度较高，改变单独某个参数意义不大，须结合攻角控制程序进行改变，有利于对HBG的整体设计。■

[1] Wade M. Saenger bomber[EB/OL].[ 2014-12-03].http://www.astronautix.com/lvs/saenger.htm.

[2] 关世义.基于钱学森弹道的新概念飞航导弹[J].飞航导弹,2005,17(1)：245-248.[3] Wall R. Darpa contemplates:hypersonic spaceplane demo[J].Aviation Week &Space Technology,2002,157(9)：81-85.

[4] 杨秀霞，张毅，施建洪，等.助推-滑翔飞行器轨迹设计研究综述[J].海军航空工程学报，2012,27(3)：245-252.

[5] 贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,1993.

[6] 甘楚雄,刘翼湘.弹道导弹与运载火箭总体设计[M].北京:宇航出版社,1989.

[7] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997.

[8] 马英，何麟书.实现高超声速跳跃式弹道关键问题的研究[J].弹道学报，2009,21(1):35-38.

[9] He Linshu.Solid ballistic missiles design[M].Beijing:Beihang University Press,2004:49-50.

[10]Corporation TP.A common aero vehicle model, description, and employment guide[EB/OL].[2014-12-03].http:∥www .dtic. mil/matris/sbir/sbir041/srch/af031a. doc.

Study on mid-course trajectories for the hypersonic boost-glide aircraft

Xu Shenda, Wu Jing, Wang Xueying

College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410000，Hunan，China)

A design of mid-course trajectory for the hypersonic boost-glide aircraft is proposed, and the trajectory characteristic is analyzed through simulations. Firstly the concept of hypersonic boost-glide aircraft and essential trajectory are introduced, and the weakness of traditional trajectory design is analyzed. Secondly a design of mid-course trajectory which is based on the motorized dominate program and the engine transient ignition is proposed, considering the real time and accurate air power and the gravity of the earth. And ignition times, ignition height and the size of the thrust are analyzed for the trajectory simulation when the motorized dominate program is invariant. Finally, the analysis of simulation results show the feasibility of the method, the advantages of overall design and the performance superiority in raising the range and improving the penetration ability.

hypersonic boost-glide aircraft；trajectory；motorized dominate program；trajectory simulation

2014-12-13；2015-01-12修回。

徐申达(1992-)，男，硕士研究生，主要研究方向为目标特性分析与目标跟踪技术。

V412.4

A