基于相位差分算法的多相编码信号实时脉内识别技术

邹梦然，陈永游，曾德国，李志鹏

(中国航天科工集团8511研究所，江苏 南京 210007)

基于相位差分算法的多相编码信号实时脉内识别技术

邹梦然，陈永游，曾德国，李志鹏

(中国航天科工集团8511研究所，江苏 南京 210007)

为解决多相编码信号识别的难题，提出一种基于相位差分算法的脉内识别方法。首先研究相位差分的原理，提出一种改进的相位解模糊方法。然后基于多相编码信号相位跳变峰的成组和递增/递减特征，提出了一种工程可实现的多相编码信号的实时识别方法。仿真结果表明，算法在3dB信噪比下对常规、线调、BPSK、QPSK信号的识别概率大于90%；而在10dB信噪比下对多相编码信号能达到90%以上的识别概率。

相位差分；相位解模糊；多相编码信号

0 引言

复杂雷达信号的脉内调制识别一直是电子对抗的关键技术和难题。现代雷达为了提高探测距离，同时保证距离分辨能力，大量使用具有大的时间带宽积的线性调频(LFM)或相位编码等复杂调制雷达信号。利用脉内调制信号类型识别技术辨识雷达的脉内调制样式，可以有效改善电子情报截获设备的识别性能[1]。

目前研究较多的识别方法有小波变换法[2]、谱相关[3]、高阶累积量法[4]和相位差分法[5]等。小波变换适合探测信号中的瞬态突变现象，但小波基选择和计算都较复杂；谱相关理论在识别具有周期平稳性的调制信号时有较大优势，但需要对多个脉冲积累；高阶累积量法利用高斯噪声的统计特性,具有较好的抗噪性能，但计算复杂，实时处理难度较大且不能适应非对称类噪声。而相位差分法计算量小，便于硬件实时实现。

本文以相位差分算法为基础，考虑高斯噪声对相位的影响，提出了一种修正相位解模糊门限的方法，并且基于对P1、P2、P3、P4及Frank编码信号相位差分曲线的研究，提出了一种多相编码信号的识别方法。

1 相位差分方法

设射频信号经过变频预处理及采样后，得到I、Q两路的数字信号为：

XI(n)=b(n)cos(2πnfc/fs+φ(n)+φ0)

(1)

XQ(n)=b(n)sin(2πnfc/fs+φ(n)+φ0)

(2)

式中，fc是中频信号频率，fs是中频采样率，φ(n)是调制函数，φ0是初始相位，b(n)为信号包络，对于常规信号、LFM、BPSK、QPSK及多相编码信号b(n)=A为常数。

信号的瞬时相位为：

θ(n)=2πnfc/fs+φ(n)+φ0=

arctan(XQ(n)/XI(n))

(3)

接收到的雷达信号，其常用的调制方式有常规信号、LFM、常规编码信号(BPSK /QPSK)及多相编码信号等，对应的一阶相位差分为：

f1(n)=θ(n)-θ(n-1)=

(4)

式中，k是线调斜率，C1(n)是0,1码元序列，C2(n)是0,1,2,3码元序列，a(n)是多相编码序列。故对于常规信号，相位一阶差分是常数；对LFM信号一阶差分随n增大而线性增大；对相位编码信号，在无相位跳变的地方是常数，当有相位跳变时存在一个附加的跳变值，具体跳变值与编码的调制信号有关，从而可以根据以上特征识别不同调制方式的信号。

由于瞬时相位容易受噪声等因素的影响，为了提高算法在低信噪比条件下的适应能力，需要进行多重相位差分。

(5)

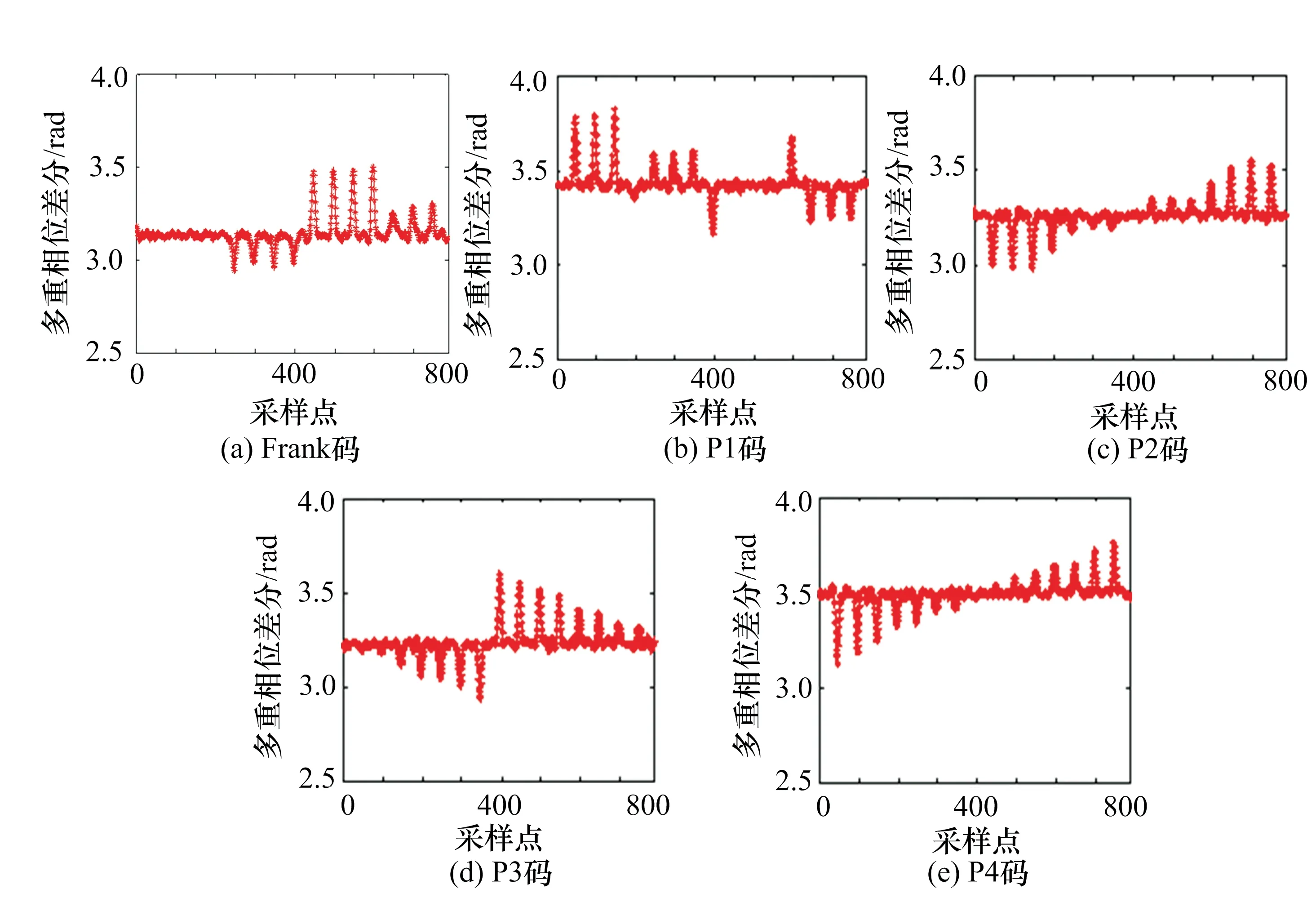
图1 5种多相编码信号的相位差分曲线

设f1(n)中的噪声服从均值为0、方差为σ2的高斯分布。可知，fN(n)中的噪声服从均值为0、方差为σ2/N的高斯分布，而N重差分后，信号的能量相对于1重差分基本不变。由此可推知，N重相位差分信噪比大约提高了10lgN1/2dB[1]。

从式(5)还可以看出N重差分时，相位编码信号的相位跳变区域会扩大为2N点。在实际工程应用中，差分重数N的选取是由信号处理器的运算能力、所需处理信号的最低信噪比和最小码元宽度等因素综合决定的。

2 多相编码信号模型

随着雷达信号越来越复杂，出现了一类多相编码信号如P1、P2、P3、P4及Frank编码信号[6]，这类信号有较好的脉冲压缩特性，其相位序列、相邻相位的差值和差分曲线如图1所示。

2.1 Frank码编码信号

Frank码编码信号的相位序列为：

θp,q=2π(p-1)(q-1)/M1/2

p=1,2,…，M1/2;q=1,2,…，M1/2

(6)

Frank码编码信号相邻相位的差值为：

θp,q+1-θp,q=

2(p-1)qπ/M1/2-2(p-1)(q-1)π/M1/2=

2(p-1)π/M1/2;p=1,2,…，M1/2;

q=1,2,…,M1/2-1

(7)

下标p变为p+1时相邻相位的差值为：

θp+1,1-θp,M1/2=-2(p-1)(M1/2-1)π/M1/2

=2(p-1)(1-/M1/2)πM-1/2

p=1,2,…，M1/2-1

(8)

考虑到相位2π的周期性，以及在相位差分曲线中相位差为Δθ和2π-Δθ的跳变仅表现为跳变峰方向相反，但是跳变峰幅度相同，所以相位解模糊之后：

2(p-1)(1-M1/2)π/M1/2=2(p-1)π/M1/2

(9)

Frank码编码信号相位差分曲线特点：从公式(7)、(9)和图1(a)可以看出Frank码的相位差分时频曲线中相位跳变成组出现，且相邻组的两个相位差是固定值。

2.2P1码编码信号

P1码编码信号的相位序列为：

θp,q=-π(M1/2-(2q-1))((q-1)M1/2+

(p-1))/M1/2

p=1,2,…，M1/2;q=1,2,…，M1/2

(10)

P1码编码信号相邻相位的差值为：

θp,q+1-θp,q=-π((M1/2-2q-1)(qM1/2+p-1)-

(M1/2-2q+1)((q-1)M1/2+p-1))/M1/2

=-π(M1/2-4q+1)+2(p-1)π/M1/2

=2(p-1)π/M1/2

p=1,2,…，M1/2;q=1,2,…，M1/2-1

(11)

下标p变为p+1时相邻相位的差值为：

θp+1,1-θp,M1/2=-π((M1/2-1)p-

(M1/2-(2M1/2-1))((M1/2-1)M1/2+(p-1)))/M1/2

=(2p-1)π/M1/2

p=1,2,…，M1/2-1

(12)

P1码编码信号相位差分曲线特点：从公式(11)、(12)和图1(b)可以看出,P1码的相位差分时频曲线成组出现，M1/2-1个相同跳变和一个不同跳变组成一组。

2.3 P2码编码信号

P2码编码信号的相位序列为：

θp,q=π(M1/2-(2q-1))(M1/2-(2p-1))/(2M1/2)

p=1,2,…，M1/2;q=1,2,…，M1/2

(13)

P2码编码信号相邻相位的差值为：

θp,q+1-θp,q=π((M1/2-(2q+1))(M1/2+1-2P)-

(M1/2-(2q-1))(M1/2+1-2p))(2M1/2)-1

=π(M1/2+1-2p)/(2M1/2)

p=1,2,…，M1/2;q=1,2,…，M1/2-1

(14)

下标p变为p+1时相邻相位的差值为：

θp,q+1-θp,M1/2=π((M1/2-1)(M1/2-1-2p)-

(M1/2-(2M1/2-1))(M1/2+1-2p))(2M1/2)-1

=π(M1/2-2p)(M1/2-1)/M1/2=2πp/M1/2

p=1,2,…，M1/2-1

(15)

P2码编码信号相位差分曲线特点：从公式(14)、(15)和图1(c)可以看出，P2码的相位差分时频曲线成组出现，M1/2-1个相同跳变和一个不同跳变组成一组。可见P1、P2码特征非常相似，很难区分。

2.4 P3码编码信号

P3码编码信号的相位序列为：

θp=π(p-1)2/Mp=1,2,…，M

(16)

P3码编码信号相邻相位的差值为：

θp+1-θp=πp2/M-π(p-1)2/M=2pπ/M-π/M

(17)

P3码编码信号相位差分曲线特点：从公式 (17)和图1(d)可以看出P3码的每次相位差递增，固定递增2π/M。

2.5 P4码编码信号

P4码编码信号的相位序列为：

θp=π(p-1)2/M-π(p-1)p=1,2,…，M

(18)

P4码编码信号相邻相位的差值为：

θp+1-θp=πp2/M-πp-π(p-1)2/M+π(p-1)

=2pπ/M-π(N+1)/M=2pπ/M-π/M

(19)

P4码编码信号相位差分曲线特点：从公式 (19)和图1(e)可以看出P4码的每次相位差递增，固定递增2π/M。可见P3、P4码特征非常相似，很难区分。

综上所述，Frank、P1、P2码的相位差分时频曲线中相位跳变成组出现，Frank码每一组相位跳变由M1/2个相同的跳变组成，而P1、P2码每一组相位跳变由M1/2-1个相同的跳变和1个不同的跳变组成；P3、P4码的相位差分时频曲线中相位跳变具有递增/递减关系。

3 相位解模糊

实际中通过反正切以及实部虚部的正负得到的只是-π～π的相位，因此会造成相位差的不连续性，所以相位差分之前需要对相位进行相位解模糊。相位解模糊的基本原理如下：

无模糊相位：

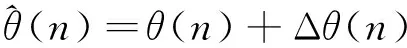
(20)

对于门限T的选定，根据最小错误概率准则推出的最佳门限为[7]：

T=2πfc/fs-π+ln(fc/(fs-fc))/(πA2/σ2)

(21)

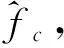
根据相位噪声的概率密度函数公式[8]：

p(Δφ)=(2π)-1exp(-d2/2)+

(2π)-1/2dcos(Δφ)exp-2-1d2(sin(Δφ))2Ф(dcos(Δφ))

(22)

式中，Δφ为相位噪声，d=A/σ，d2/2 等于信噪比，Φ为标准正态分布的分布函数。相位噪声概率密度函数曲线如图2所示。

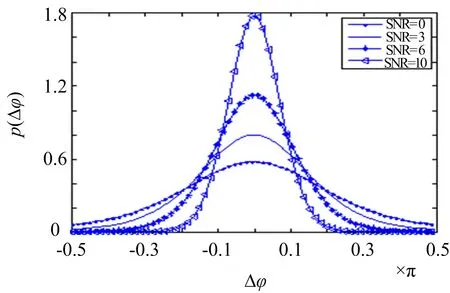
图2 相位噪声概率密度函数

由于FFT运算存在量化误差。当输入信号的频率不在FFT量化频率点处时，直接用FFT运算的最大谱线位置来估计正弦输入信号的频率，将存在量化误差，其误差范围为[-fs/(2L),fs/(2L)][9]，其中，L为FFT点数。对应的数字频率误差范围为[-π/L,π/L]，若对L=16应的频率误差范围是[-π/16,π/16]，取最大的频率误差求得出现解模糊错误时最小的相位噪声为15π/16，代入相位噪声的计算公式得：信噪比等于3 dB时，解模糊失败的概率为0.14%，可以满足后续算法要求。

4 信号调制识别

本节将分析常规、线调、BPSK、QPSK、多相编码信号的时频曲线，并提取信号带宽、线性度、跳变峰幅度、不同类型跳变点个数等特征用于区分各类信号。4种典型调制信号的相位差分曲线如图3所示。

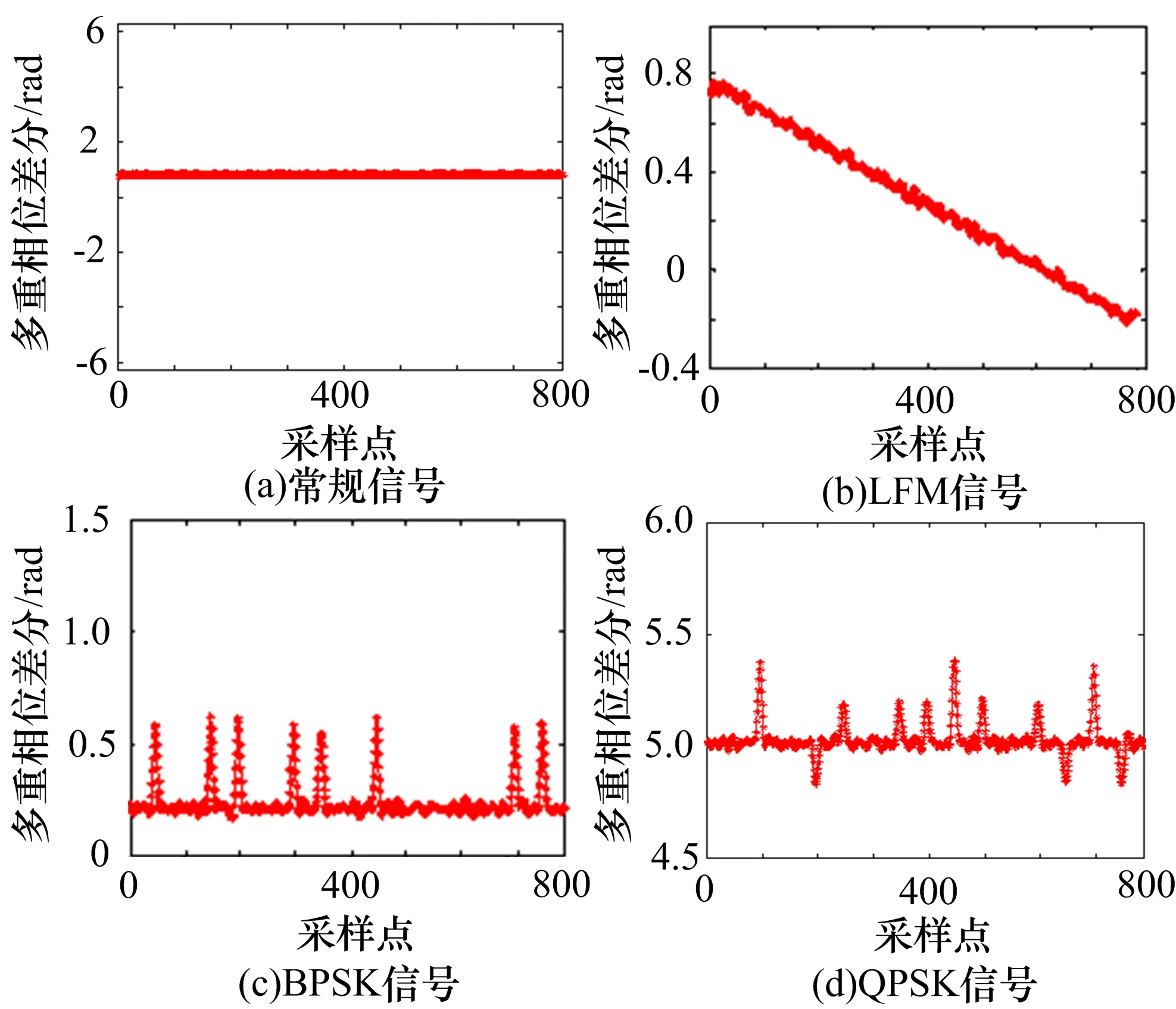
图3 4种典型调制信号的相位差分曲线

从常规、线调、BPSK、QPSK、多相编码信号的相位差分曲线可以看出，可以利用峰值检测提取出相位跳变峰，而去除相位跳变峰之后的差分曲线除了线调信号都近似一条直线，于是定义去相位跳变后的曲线最大最小值之差作为信号的带宽，用于区分宽带信号和窄带信号，并用最小二乘法估计的均方误差σLMS作为曲线线性度的度量，用于区分线调信号和NLFM信号。

多相编码信号的相位差分曲线和常规编码信号一样都是由单载频加上跳变峰组成。所以，对于窄带信号通过判断有无相位跳变峰可以分离出常规信号。然后，考虑到多相编码信号的相位跳变峰幅度和常规编码信号不同，可以通过幅度区分不同类型的跳变峰，N重相位差分曲线中π，π/2,3π/2跳变峰对应的幅度分别为：π/N,π/(2N),3π/(2N)。统计跳变π,π/2,3π/2和非π,π/2,3π/2跳变的数目，并根据π,π/2,3π/2跳变占总跳变数的比例是否大于门限，区分信号是属于常规调相信号还是属于多相编码信号。

随机码元序列的QPSK信号π的相位跳变占总跳变数的1/3，所以对于常规调相信号，π的相位跳变所占比例超过门限判为BPSK，否则判为QPSK，在相位跳变个数较多的情况下根据最小错误概率准则该门限应取为2/3。

图4 信号脉内调制识别流程图

在多相编码信号中，Frank码的相位差分时频曲线中相位跳变成组出现。P1/P2码的相位差分时频曲线中相位跳变成组出现，但是每组都有一个不相同的跳变。P3/P4码的相位差分时频曲线中相位跳变有递增递减关系。所以记录下相位跳变的幅度和位置，并通过分析其成组关系和递增递减关系判别多相编码信号。但是考虑到噪声影响P1/P2码可能会出现某个跳变检测不到，而P3/P4码可能并不会严格递增递减。所以在判决时P1/P2码并不要求每一组都含有幅度不同的跳变，而P3/P4码允许出现相邻的两个跳变和其他跳变递增递减规律不同，但是不能超过一定比例。

5 算法仿真和性能分析

综上所述，本文对常规、LFM、NLFM、BPSK、QPSK、P1/P2、P3/P4、Frank码信号的相位差分曲线识别流程如图4所示。中频信号的采样率fs=10 MHz，信号持续时间80μs，相位差分重数N=8。在信噪比SNR为3、6、10dB的情况下，分别对常规、LFM、BPSK、QPSK、Frank、 P1、 P2、 P3、P4码调相信号进行仿真。

信号具体参数为：常规信号载频fc=5 MHz；线调信号载频fc=1 MHz，带宽8 MHz；BPSK/QPSK调相信号载频fc=5 MHz，码元宽度500 ns，码元序列随机；多相编码信号载频fc=5 MHz，码元宽度500 ns，M=16。实验次数为100次。100次蒙特卡洛试验结果如表1所示。

通过表1可以看出本文中提出的算法在3 dB信噪比条件下对常规、线调、BPSK、QPSK信号的识别概率大于90%，但是对多相编码信号的识别需要更高的信噪比；在6 dB和10 dB信噪比条件下算法对多相编码信号基本能达到90%以上的识别概率。

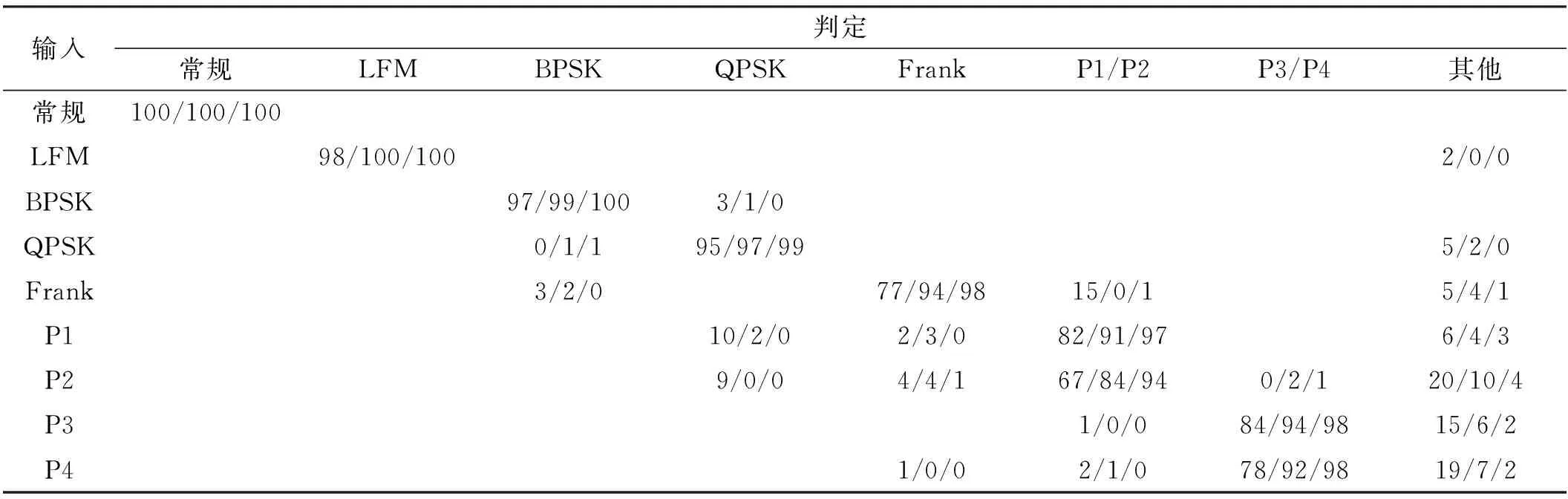
表1 SNR为3、6、10dB时,100次蒙特卡洛试验结果

6 结束语

本文在相位差分的基础上讨论了相位解模糊门限的选取，提出了利用信号的短时傅里叶频率修正解模糊门限的方法，并从理论上进行了分析。本文重点分析了Frank、P1、P2、P3、P4码调相信号等5种多相编码信号的相位差分特征，并提出了一种工程可实现的识别方法，并加以仿真验证。仿真结果说明在信噪比大于3dB时，算法对常规、线调、BPSK、QPSK信号的识别概率大于90%；在信噪比大于10dB时，算法对多相编码信号的识别概率大于90%。■

[1] 曾德国,熊辉,龙柯宇,等.基于相位差分的脉内调制信号类型识别[J].电子测量与仪器学报,2009,23(10):85-90.

[2] 廖传军,罗晓莉,李学军.小波包在声发射信号特征提取中的应用[J].电子测量与仪器学报,2008,22(4):79-85.

[3] 陈健,阔永红,李建东,等.基于小波变换的数字调制信号识别方法的研究[J].电子与信息学报,2006,28(11):2026-2029.

[4] Barbarossa S,Scaglione A,Giannakis GB.Product high-order ambiguity function for multicomponent polynomial-phase signal modeling[J].IEEE Transactions on Signal Processing,1998,46(3): 691-708.

[5] 黄知涛,周一宇,姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J]. 通信学报,2003,24(4):153-160.

[6] Yang Jie,Sarkar TK.A new doppler-tolerant polyphase pulse compression codes based on hyperbolic frequency modulation[R].IEEE Transactions on Radar Conference,2007:265-270.

[7] 宋云朝,万群,毛祺,等.一种稳健的基于解卷叠的相位差分瞬时测频方法[J].电子信息对抗技术,2008,23(4):12-15.

[8] 赵树杰,赵建勋.信号检测与估计理论[M].北京:清华大学出版社,2005.

[9] 王旭东,刘渝,邓振淼.基于修正Rife算法的正弦波频率估计及FPGA实现[J].系统工程与电子技术,2008,30(4):621-624.

Realtime recognition of polyphase pulse compression codes based on phase difference

Zou Mengran, Chen Yongyou, Zeng Deguo, Li Zhipeng

(No.8511 Research Institute of CASIC,Nanjing 210007,Jiangsu,China)

Based on phase difference,a recognition approach for polyphase pulse compression codes is presented. First, the principle of phase difference is studied, and the improvement method of phase unwrapping is presented and derived.Second,a polyphase pulse compression codes realtime recognition flow is shown based on the group character of phase hopping and the monotonic increase or decrease of hopping.Simulation results show that the algorithm can achieve the recognition probability of more than 90% for the common radar signals in 3dB SNR and the polyphase pulse compression codes in 10dB SNR.

phase difference;phase unwrapping;polyphase pulse compression codes

2014-12-22；2015-02-26修回。

邹梦然(1990-)，男，硕士研究生，主要研究方向为信号及信息处理。

TN971+.1

A