基于FRFT的抗线性函数移频干扰算法研究

张柏林, 吕亚昆, 赵凯凯

(空军航空大学，吉林 长春 130022)

基于FRFT的抗线性函数移频干扰算法研究

张柏林, 吕亚昆, 赵凯凯

(空军航空大学，吉林 长春 130022)

线性函数移频干扰可以对线性调频脉冲压缩雷达形成有效的压制性干扰，改变载频和调频斜率均无法有效对抗线性函数移频干扰。通过分析线性函数移频干扰对线性调频脉冲压缩雷达的干扰效果和原理，提出了基于FRFT的抗线性函数移频干扰算法，从理论上分析了该算法的可行性，最后通过仿真验证了该算法的正确性和可行性。

线性函数移频干扰；脉冲压缩；压制干扰；抗干扰

0 引言

线性调频脉冲压缩雷达发射时采用宽脉冲进行目标探测，接收时进行脉冲压缩，因而具有高的辐射能量和高距离分辨率，同时接收时采用匹配滤波因而具有很强的抗噪声干扰和假目标欺骗干扰的能力，因此被广泛应用到现代雷达系统中。当采用传统的噪声调幅等干扰样式对其进行干扰时，由于雷达接收时进行匹配接收，匹配滤波器的系统响应函数与信号匹配，而与噪声调幅干扰等信号失配，匹配滤波后输出信号的信干比较匹配滤波前改善压缩比BT倍(B为线性调频信号的带宽,T为信号脉冲宽度)。而线性调频信号的压缩比通常可以达到几十到几千，如果想取得预期的干扰效果，干扰机的输出干扰信号的功率必须比回波信号的功率大BT倍以上,这是十分困难的。文献[1～4]提出了几种改进的移频干扰样式，移频干扰是利用线性调频信号的距离-速度之间的强耦合性，来实现导前假目标干扰，但是雷达可利用改变调频斜率和相参积累来对抗该假目标欺骗干扰。文献[4]提出利用移频干扰实现压制干扰的干扰算法，通过改变发射信号的调频斜率和利用相参积累均不能显著改善干信比，可对线性调频信号形成较为有效的遮盖干扰，给雷达带来严峻的挑战。为了有效对抗线性函数移频干扰，本文提出一种基于FRFT(分数阶傅里叶变换)的抗干扰算法，首先分析了线性函数移频干扰的作用原理，然后对抗干扰算法进行了理论分析并给出了算法的实现流程，最后通过仿真实验证明了该算法的有效性。

1 线性函数移频干扰

1.1 线性函数移频干扰原理

为了便于分析，设雷达接收到的LFM回波信号为：

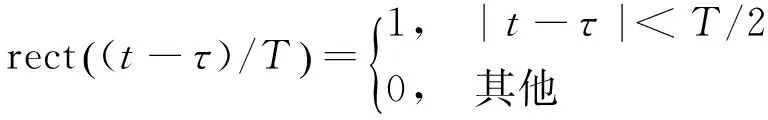
(2)

式中，f0为信号载频，fd为目标运动产生的多普勒频移，τ为目标距离对应的时延，u=B/T为调频斜率，B为带宽，T为脉宽。

匹配滤波器系统响应函数为：

h(t)=u1/2rect (t/T)exp(j2πf0t-jπut2)

(3)

匹配滤波后，目标信号输出为：

线性函数移频干扰是使移频值在雷达脉冲持续时间内随时间进行线性变化，即Δf=Δf0+u′t，Δf0为线性函数移频干扰的移频起始频率，u′为移频的调频斜率。则干扰信号为：

sj(t)=rect((t-τ)/T)A′exp(j2π(f0+fd+ Δf0)(t-τ)+jπ(u+u′)(t-τ)2)

(5)

假设进行线性函数移频干扰时的移频斜率为正。

1)当Δf0+fd-u′T>0，Δf0+fd+u′T>0时

进行匹配滤波后输出信号的频谱为：

Yj(ω)=rect(((ω-2πf0+(πu′T/2)-πΔf0- πfd)/(2πB+2πu′T-2πΔf0))B(u+u′)-1/2exp((ω-2πf0)2/(4πu)- (ω-2πf0-2πΔf0-2πfd)2/(4π(u+u′))-ωτ)

(6)

对上式进行傅里叶反变换得匹配后的干扰信号为：

yjout=A′(u/u′)1/2exp(j 2πf0(t-τ)-πu(u+u′)(t-τ)2/u′-2πu(Δf0+fd)(t-τ)/u′-π(Δf0+fd)/u′-π/4)

τ-(u′T+2Δf0+2fd)/(2(u+u′))≤t≤τ-(2Δf0+2fd-u′T)/(2u)

(7)

干扰信号宽度为：tw=(2uu′T-2u′(Δf0+fd))/(2u(u+u′))。

2)当Δf0+fd-u′T<0，Δf0+fd+u′T>0时

干扰信号宽度为：τ-(Δf0+fd-u′T/2)/(u+u′)≤t≤τ+|f0+fd-u′T/2|/(u+u′)

3)当Δf0+fd-u′T<0，Δf0+fd+u′T<0时

干扰信号宽度为：τ-|Δf0+fd-u′T/2|/(u+u′)≤t≤τ+|f0+fd-u′T/2|/(u+u′)

由以上讨论可知：

1)线性函数移频干扰经匹配滤波后输出干扰信号幅度近似为A′(u/u′)1/2，与匹配滤波前幅度之比为(u/u′)1/2；

2)干扰信号压缩后输出形成幅度近似恒定的干扰带，对于不同的Δf0和u′，干扰信号产生遮盖干扰的干扰带宽不同，且干扰信号不随调频斜率和载频的变化而改变遮盖位置。

1.2 干扰仿真

设线性调频信号的脉宽为10μs，载频f0为100MHz ，带宽B=30MHz ，目标回波时延τ=100μs,调频斜率u=3MHz/μs，A=1，fd=0Hz，线性函数移频干扰的移频起始频率Δf0=0MHz ，移频斜率u′=500kHz/μs。在进行线性函数移频干扰中设干扰机的增益为A′=7。对接收到的信号进行线性函数移频干扰时，雷达接收到的信号进行脉冲压缩后的波形仿真结果如图1(a)所示。

改变带宽使B=50MHz ，脉宽等参数不变，即改变调频斜率使u=5MHz/μs，其他条件不变，仿真后得到图1(b)。改变载频使f0为150MHz ，其他条件不变，进行计算机仿真，得到仿真图形如图1(c)所示。对比图(a)、(b)和(c)可知，改变调频斜率和载频无法有效消除干扰信号。

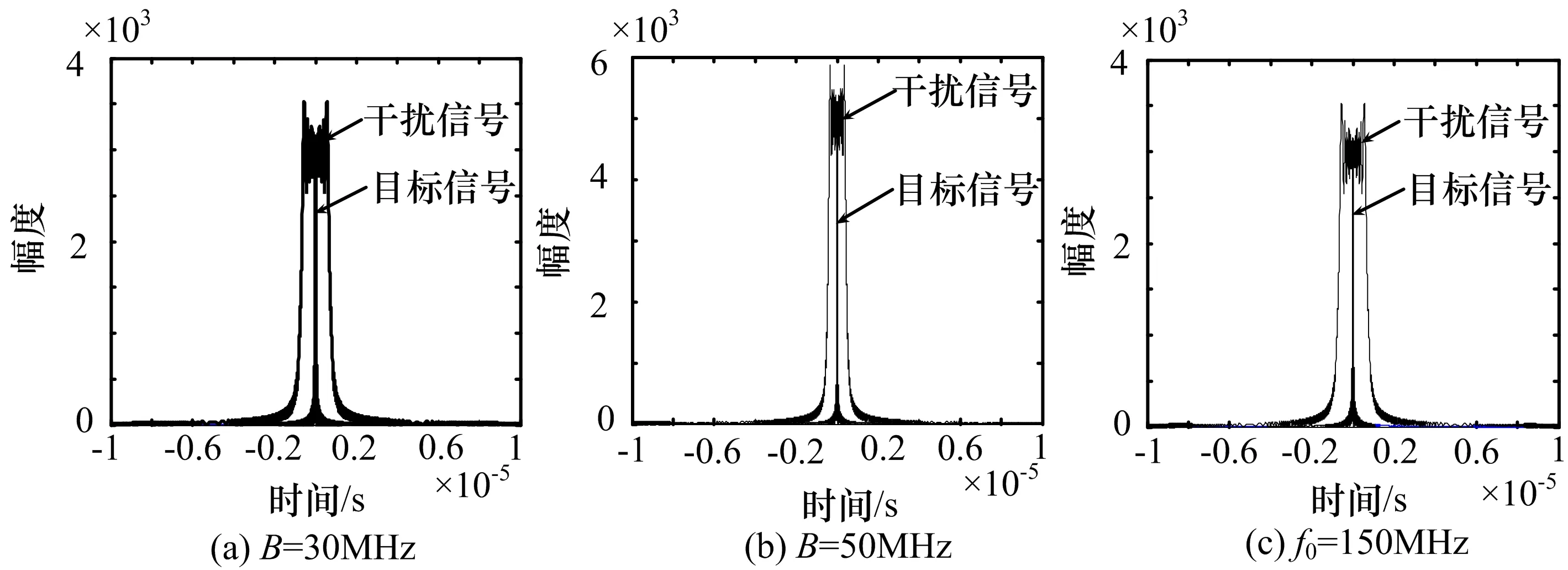
图1 线性函数移频干扰

2 抗干扰算法

2.1FRFT

传统的Fourier变换仅将时域和频域结合起来，只能反映各个频率分量，不能有效地反映信号的频率随时间的变化情况，是分析确定性信号和平稳信号的一种好工具，但不能用来分析非平稳信号。对于非平稳的LFM信号的分析必须采用时频分析的方法，时频分析是可以将时域信号映射到二维的时频平面，时频平面反映了信号的各频率成分随时间变化的分布情况。Fourier变换可以看作是将信号在时频平面上从时间轴逆时针旋转π/2到频率轴;而FRFT变换可以看作在时频平面进行旋转任意角度α的变换。因此结合Fourier变换的定义可以定义信号的FRFT。

信号f(t)的p阶FRFT定义为:

(8)

式中，FRFT的核函数Kp(u,t)为:

式中，Aa=exp(-jπsgn(sina)/4+ja/2)/|sina|1/2，a=pπ/2。当分数阶次p=1时，Aa=1，则：

可见f1(u)就是f(t)的Fourier变换。同样，f-1(u)是f1(u)的Fourier逆变换。由此，可以将FRFT看作是一种广义的Fourier变换。因为核函数中a=π/2，a1=p1π/2仅出现在三角函数的参数位置上，所以，以p为参数的定义是以4为周期的，因此只需对区间p∈(-2，2]考虑即可。当p=0时，f0(u)=f(u)，当p=±2时，f±2(u)=f(-u)。

2.2 基于FRFT的抗线性函数移频干扰算法

FRFT是一种线性变换，FRFT在与给定的LFM信号的调频斜率相一致的分数阶域内呈现脉冲函数特征,此时FRFT域谱峰位置u0与信号的变换角度a0满足以下关系：

(9)

通过对LFM信号连续进行FRFT变换,在分数阶域内搜索其局部极大值,就可以实现对LFM信号的检测和参数估计。局部极大值对应的变换角度对应LFM信号的调频斜率。线性函数移频干扰信号与目标信号可以看成是多分量信号的处理问题。由于线性函数移频干扰的作用原理是改变原有信号的调频斜率，因此在对干扰和目标信号进行接收处理时，线性函数移频干扰可以看成与目标回波信号调频斜率不同的信号，而目标信号的调频斜率已知，因此可以利用FRFT变换搜索找到干扰信号调频斜率对应的变换角度，根据估计得到的参数对干扰信号进行重构，再利用重构的信号消去干扰信号，从而完成干扰信号的滤除。在对雷达进行线性函数移频干扰时，为达到干扰雷达的目的，干扰信号能量往往远远高于目标信号，根据文献[7]所述，强信号分量会对弱信号分量形成遮盖作用，因此在利用FRFT进行检测时会先将干扰信号分量检测出来，再根据式(9)完成对干扰信号的参数估计，因此在理论上可以利用FRFT完成干扰信号与目标分离。

根据上文分析可知调频斜率变化越大，干扰信号与匹配接收机失配越严重，干扰信号所获得的增益越小，因此在实际中|u′|<0.5u，可以利用此结论来缩小FRFT变换的角度搜索范围，从而提高该算法的处理速度。

具体算法步骤为：

1)对接收到的干扰和目标信号进行FRFT变换得到x(a,u)，对x(a,u)进行谱峰搜索；

2)根据所搜索到谱峰的坐标，利用公式(9)完成干扰信号的参数估计；

算法流程图如图2所示。

图2 算法流程

当存在多个干扰信号时，可以将干扰信号从强到弱依次消除，直到检测到的峰值对应的为目标信号。

3 仿真实验

由2.2节可知，抗算法算法的有效性，依赖于对干扰信号的正确估计，对干扰信号的估计精度由FRFT的搜索步长决定，搜索步长越小估计精度越高，然而计算量也会相应地增加，通过对FRFT进行双尺度搜索可以有效减少计算量提高估计精度，即先采用大的搜索步长L1来粗略定位干扰信号，然后用L2来对干扰信号进行精确估计。

为了便于分析，选取线性调频信号作为发射信号，其载频为f0=100MHz ，脉宽T=10μs ，采样频率为fs=400MHz ，带宽B=30MHz ，调频率u=3MHz /μs，接收信号时延τ=0μs ，设目标多普勒频移fd=0Hz ，线性函数移频干扰的Δf0=0MHz ，移频斜率u′=500kHz/μs，干信比JSR=10dB，噪声信号为高斯白噪声，信噪比SNR=-5dB。

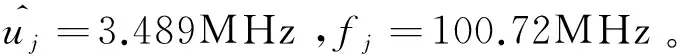
图3 尺度L1=0.2时FRFT变换的幅度图

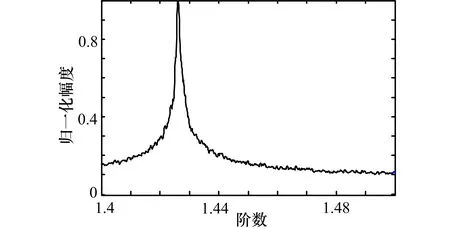
图4 尺度L2=0.001时FRFT变换的幅度图

图5 干扰滤除后匹配滤波输出波形

由以上实验可知，采用FRFT对干扰信号进行参数估计，利用估计得到的参数对干扰信号进行重构，再通过重构的信号将干扰信号滤除，可以取得很好的抗线性函数移频干扰效果。通常情况下干扰信号功率较大，因此很容易被检测估计，由于受估计精度的影响，干扰信号不能被完全滤除，大量实验证明当调频斜率估计误差不大于0.5%、载频误差不大于1%时，通过估计干扰信号参数来进行重构滤波，此时估计误差不影响正常的目标检测。

4 结束语

本文分析了线性函数移频干扰的干扰原理以及频谱特性，在此基础上提出了一种基于FRFT的抗线性函数移频干扰算法，从理论上分析了该算法的原理并给出了相应的实现步骤，最后通过仿真实验验证了该算法的正确性与可行性。随着对FRFT算法研究的深入，FRFT可以通过FFT快速实现，因此可以将其应用到工程实践中，具有很高的实际应用价值。■

[1] 王玉军，赵国庆，胡曦明. 基于延迟不变的LFM雷达移频干扰研究[J].系统工程与电子学报，2009，31(8)：1861-1863.

[2] 吕波，冯起，袁乃昌. 对LFM脉压雷达的移频压制干扰技术研究[J].现代雷达，2009，31(1)：9-12.

[3] 王玉军，赵国庆.对LFM雷达的N阶SSC盲移频干扰算法[J].电路与系统学报，2011，16(4)：70-74.

[4] 黄洪旭，周一宇.干扰合成孔径雷达的时延脉间抖动转发干扰模式研究[J].兵工学报，2012，33(9)：1031-1035.

[5] 席泽敏，贺静波.线性调频脉冲压缩雷达干扰仿真研究[J].现代雷达，2005，27(10)：5-7.

[6] 黄翀鹏，王剑，徐保国.线性调频脉冲的移频干扰性能研究[J].系统工程与电子技术，2013，35(5)：935-939.

[7] 李宝，关键，郭海燕.LFM信号的FRFT模函数对称特性及参数估计[J].雷达科学与技术，2008，6(3)：210-214.

[8] 朱建东，赵拥军，唐江.线性调频连续波信号的周期分数阶Fourier变换检测与估计[J].电子与信息学报，2013，35(8)：1827-1833.

[9] 李昕，王向前.离散分数阶Fourier变换的LFM信号时延估计[J].系统仿真学报，2012，24(4)：756-760.

[10]朱良，曹鹏，禹卫东.基于移频干扰的成像算法抗干扰性能研究[J].电子学报，2011，39(3A)：47-51.

An algorithm against linear frequency-shifting jamming based on FRFT

Zhang Bolin, Lü Yakun, Zhao Kaikai

(The University of Air Force,Changchun 130022,Jilin,China)

A linear frequency-shifting jamming can effectively form blanket jamming on LFM pulse-compression radar. Carrier frequency and chirp rate changes are not effective against the linear frequency-shifting jamming. By analyzing the interference effect and principle of the liner frequency-shifting jamming on the LFM pulse-compression radar, an algorithm against linear frequency-shifting jamming based on FRFT is put forward and the feasibility of the algorithm is analyzed in theory. Finally the correctness and feasibility of the algorithm is verified by simulation.

linear frequency-shifting jamming;pulse-compression;blanket jamming;anti-jamming

2014-10-22；2014-12-23修回。

张柏林(1990-)，男，硕士研究生，主要研究方向为航空航天电子侦察。

TN974

A