脉冲串信号的时差和频差估计新方法*

肖学兵，郭福成，姜文利

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

脉冲串信号的时差和频差估计新方法*

肖学兵，郭福成，姜文利

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

针对脉冲串信号的互模糊函数多峰特性以及时差频差估计运算量大的问题，提出一种时差和频差联合估计新方法。该方法首先基于信号频差与时差变化率的关系，利用时差序列引导互模糊函数的时差频差搜索范围，然后利用脉冲串信号的时域稀疏特性改进了基于互模糊函数的时差频差估计方法。理论和仿真分析表明，该算法可有效抑制频差模糊，并在估计精度损失不大的前提下有效降低运算量。

脉冲串信号；时差；频差；互模糊函数

0 引言

时差频差定位体制利用同一辐射源信号到多个不同观测站的到达时间差(TDOA)和到达频率差(FDOA)信息，可以在被动接受条件下估计得到辐射源位置。该体制最少利用两个观测站就可以实现二维定位，最少三个观测站就可以实现三维定位。时差频差联合定位体制相对于多站测向交叉定位、时差定位等无源定位体制定位精度更高[1]，在电子侦察、预警探测和传感器网络等领域具有重要的应用价值[1-4]。雷达信号是一类重要的辐射源目标，而其信号带宽较宽、单个脉冲持续时间可能很短(μs量级)，通过分别测量雷达信号脉冲频率和到达时间来得到时差频差的方法，其估计精度很差。因此必须寻求一种新的稳健的时差频差估计算法。

针对窄带信号，Stein在文献[5]中详细论述了基于互模糊函数(CAF)的时差频差联合估计方法，提出了滤波抽取、粗精搜索和插值拟合等经典处理方式，并且进一步证明了在高斯白噪声背景下，CAF是一种最大似然估计方法[6]。为了降低CAF的运算量，文献[7～8]介绍了分维估计算法。针对相关噪声，文献[9～10]引入高阶累积量，构造了新的CAF，提高了相关噪声情况下的CAF的估计性能。但是当把上述CAF法应用到脉冲串信号时就会发现存在如下两个方面的问题：一是脉冲串信号的CAF具有多峰特性，并且真实时差频差对应峰与虚假峰幅度可能相差很小(如小于1 dB)，这样在噪声影响下就容易发生错误估计的情况；二是由于脉冲串信号的时域稀疏特性，CAF的直接计算需要对数据补零后才能进行，而且会造成大量的不必要运算。文献[11]首先提出了一种利用时差变化规律来估计时差和时间多普勒差的方法，将观测数据时域分段后分别采用互相关法估计每一段信号时差从而得到一个时差序列，继而利用时差变化规律估计出观测起始时刻的时差和时间多普勒差。但该方法得到的频差估计精度较低。

本文针对上述方法应用于脉冲串信号时差频差估计的不足，提出了一种时差序列引导CAF的时差频差联合估计新方法。通过测量脉冲到达时间(TOA)得到时差序列，然后估计时差变化率，再利用时差变化率得到观测起始时刻时差和频差的粗估值，在时差频差粗估值的小范围内进行CAF二维搜索得到时差频差的精确估计值。该算法利用时差序列缩小时差频差的搜索范围，可有效抑制频差模糊的发生。另外，本文针对脉冲串信号时域稀疏的特点对经典CAF进行一定近似计算后，提出了一种适合小范围时差频差搜索的改进CAF计算方法，可在对精度影响不大的前提下有效降低运算量。

1 时差序列引导时/频差搜索范围

若辐射源辐射的是窄带信号(带宽远小于载频)，则两个几何上分置的被动观测站接受到的信号观测模型可表示为[5]：

y1(t)=x(t)+n1(t)

y2(t)=Ax(t-τ)exp(-j2πv(t-τ))+n2(t)

(1)

式中，v为两观测站观测到信号的频差；τ为两观测站观测到信号的时差；A为两观测站观测到信号的相对幅度增益；x(t)为接收机1接收到的真实信号；ni(t)为观测噪声。其中：

v≈fc(vr2-vr1)/c

(2)

式中，fc为信号载频；vri为辐射源相对于观测站的径向速度。

对于运动轨迹平滑的低速运动目标或较短观测时间内(一般小于1s)的高速运动目标，可假设观测时间内辐射源做匀速直线运动，辐射源相对于观测站的径向速度近似保持不变[11]，则TDOA满足：

Δτ(t)≈τ0+kτt

(3)

式中，Δτ(t)为随时间变化的TDOA；τ0为观测起始时刻时差，起始时刻定义为主站(观测站1)首个脉冲的TOA；kτ为时差变化率。其中：

kτ≈(vr2-vr1)/c

(4)

对比式(2)和式(4)可知，时间差变化率kτ与频差之间存在如下关系：

v≈fckτ

(5)

由此通过对时差序列进行直线拟合估计出截距和斜率，便可估计出观测起始时刻的时差和频差。为此，可以采用最小二乘法进行拟合估计。设观测站在观测时间内接收到k个脉冲，两观测站脉冲经过分选配对后第k个脉冲对的TOA分别为t1k,t2k，Δtk=t2k-t1k表示第k个脉冲对的两脉冲分别到达两个观测站的时间差。由式(3)可得：

Δtk≈kτt1k+τ0

(6)

将式(6)表示为矩阵形式：

y=Hx+n

(7)

(8)

(9)

(10)

(11)

当通过视频包络法测量TOA时，TOA的估计均方根误差σT可近似为σT≈tr/(2γ)1/2，其中脉冲前沿从10%到90%的时间tr可近似表示为tr≈1/B，B为包络形成时低通滤波带宽，γ为中频数据信噪比。设两观测站观测噪声不相关，且观测站观测数据信噪比相等，则σΔt近似表示为σΔt≈1/Bγ1/2。

以固定脉冲重复间隔(PRI)信号为例，设积累时间0.1 s，信号带宽10 MHz，脉冲重复频率1 kHz，中频数据信噪比10 dB，信号载频1.5 GHz，频差估计均方根误差为164.3 Hz。时差序列法得到的频差估计精度并不能达到定位要求(一般在Hz量级或更小)，但是可以用来获得无模糊的频差搜索范围。通过时差序列法得到无模糊的频差搜索范围后，还要在该范围内进行CAF二维搜索得到时差频差的精确估计值。此外，雷达脉冲串信号占空比小，通常需要补零后才能进行经典CAF运算，造成大量不必要运算。针对这种情况，下面介绍一种针对脉冲信号的改进CAF计算方法。

2 脉冲串信号的CAF计算方法

设观测站接收到信号经过分选配对后有K个脉冲对，t1k,t2k分别表示观测站1和观测站2所观测到的第k个脉冲的TOA，L1k,L2k则分别表示观测站1和观测站2观测到的第k个脉冲的采样点数。由此脉冲信号可以表示为：

(12)

其中:

(13)

式中，ai为观测站i接收到信号相对于原始信号的幅度增益，fk(n)为辐射源信号第k个脉冲的脉内调制函数，包括初相、脉内调制方式的信息。

对于脉冲样点序列x1(n),x2(n)，经典的CAF计算方法为：

(14)

下面结合式(12)的信号模型，给出一种利用脉冲串信号时域稀疏特性的改进CAF计算方法。在利用TOA差值引导时差频差搜索范围后，假设时差搜索范围小于脉冲重复周期且脉冲已配对，有：

(15)

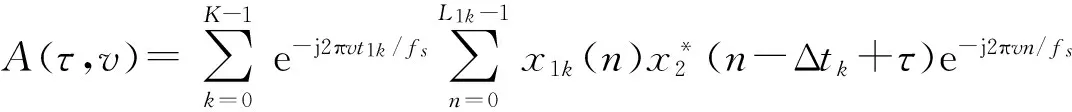
(16)

式中，Δtk=t2k-t1k，又e-j2πvn/fs≈1，所以有：

(17)

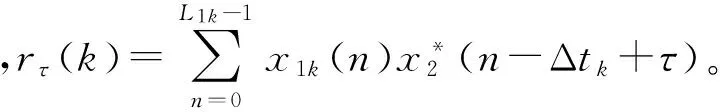
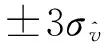
下面对比两种计算方法的运算量。设采样率fs，信号积累T，脉冲重复间隔Tp，脉冲宽度Pw，时频差的二维搜索中时差搜索Nτ点，频差搜索Nv点。另外，e-j2πvn/fs的值通过查表得到，并且需要一次实数乘法来得到数据在表中存储的位置。这样式(14)中实数乘法次数为9fsTNτNv，实数加法次数为6fsTNτNv。设处理器乘法和加法运算都可单指令周期实现，则式(11)总的运算量为15fsTNτNv。式(16)中实数乘法次数为(4PwfsT+5T)NτNv/TP，实数加法次数为(2TPwfs+T)NτNv/Tp，则式(17)的总运算量为：(6TfsPw+6T)NτNv/Tp。这样CAF经典计算方法与脉冲串信号CAF计算方法的运算量之比η为：

η=15fsTTp/(6TfsPw+6T)≈5Tp/(2Pw)

(18)

3 频差解模糊性能分析

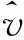
(19)

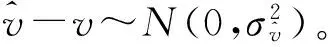
(20)

式中，频差的估计方差由式 (11)给出，解模糊成功概率可通过数值积分或者查高斯分布概率表的方法得到。结合式(11)，频差解模糊性能受中频数据信噪比、脉冲重频、信号带宽、信号积累时间等因素影响。以第1节介绍的固定重频典型应用为例，频差解模糊成功概率为99.77%，算法可有效抑制频差模糊。

4 时差频差估计仿真

4.1 时差序列法的频差估计性能

不同信噪比条件下，时差序列引导CAF得到的频差估计标准差以及频差解模糊成功的概率，如图1所示。仿真条件如下：固定PRI，重频为1kHz，信号积累时间80μs，脉内调制方式为线性调频，调制带宽5MHz，信号载频1.5GHz，信噪比范围[10dB,25dB]。

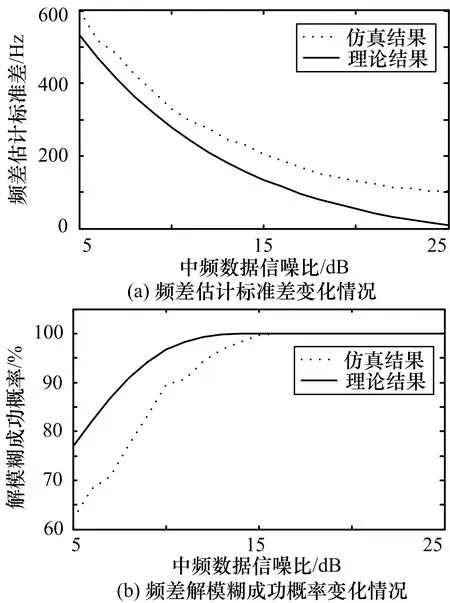
图1 频差估计性能随性噪比变化

从图1可以看出仿真结果与理论结果基本一致，随着信噪比的提高,频差解模糊成功概率增加。在信噪比大于15dB时频差解模糊成功概率可接近100%。该算法可以有效抑制频差模糊。

4.2 改进CAF计算方法的估计性能

不同信噪比条件下，脉冲串信号的CAF计算方法与经典CAF法的时差频差估计性能的对比，如图2所示。时差频差搜索范围不存在模糊，旨在研究这两种计算方法在估计精度方面的差异。仿真条件如下：脉冲重复频率1kHz，脉宽5μs，脉内调制方式为线性调频，调制带宽2MHz，时差搜索范围[-0.00002s,0.00002s]，频差搜索范围为[-500Hz,500Hz]，信噪比变化范围为[5dB,25dB]。图2显示经典CAF时差频差的估计精度略优于改进CAF计算方法，两种方法频差估计标准差的差值不大于 0.2Hz，时差估计标准差的差值不大于10ns。这主要是改进CAF法计算过程中进行了近似运算引起的。

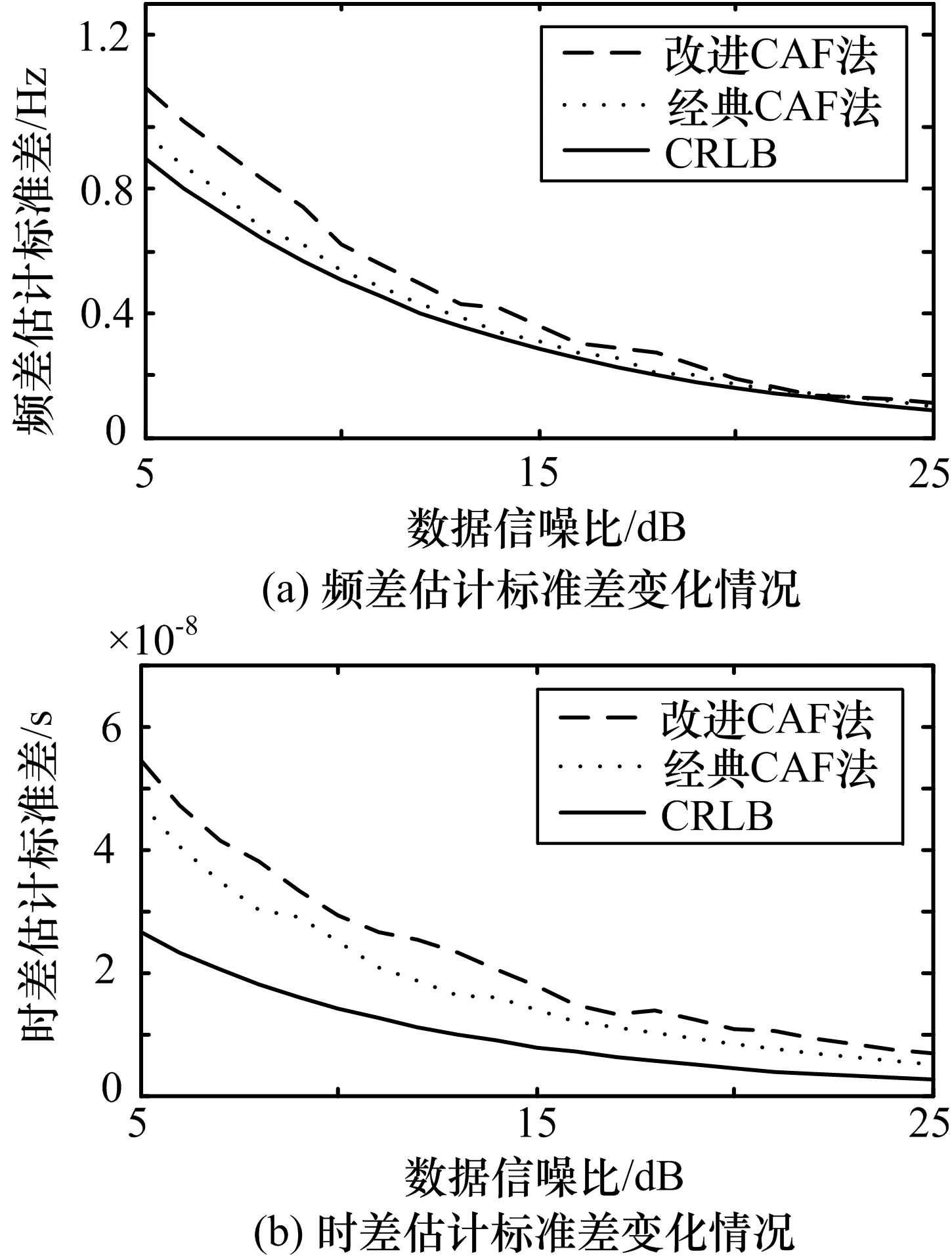
图2 时差频差估计性能

同一信号分别采用经典CAF与脉冲串信号的改进CAF计算方法所需运算时间的对比，如图3所示。仿真条件为脉宽10μs，脉冲重复频率1kHz，采样频率100MHz，脉内调制方式为线性调频，调制带宽2MHz。仿真中针对同一批数据，在相同的时频差搜索范围和搜索步进条件下分别统计两种算法程序的运行时间，在一定程度上反映两种算法运算量的大小。仿真结果表明脉冲串信号的改进CAF计算方法在运算量方面要优于经典CAF两个数量级左右，与理论分析一致。

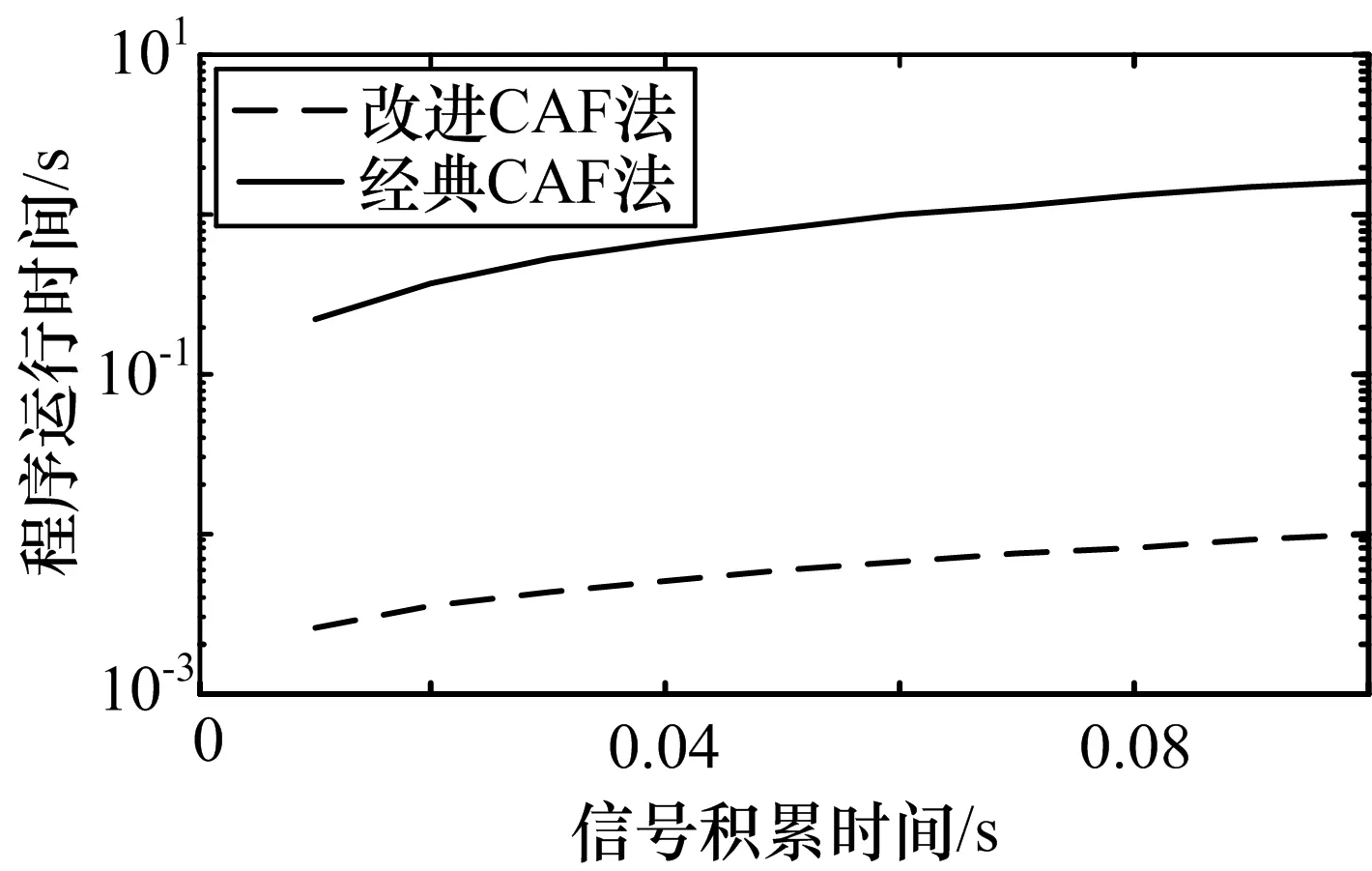
图3 算法运算时间

5 结束语

针对脉冲串信号CAF多峰特性以及传统时差频差估计方法运算量较大的特点，本文提出了一种时差序列引导CAF的时差频差联合估计新方法，并且针对脉冲串信号时域稀疏的特点对CAF计算方法做了改进。仿真分析表明该方法不仅可以有效抑制脉冲串信号的频差模糊，而且在对估计精度影响很小的前提下有效地降低了运算量。■

[1] 朱伟强，黄培康，马琴，等. 多站时差频差高精度定位技术[J]. 数据采集与处理，2010,25(3): 307-312.

[2]HoKC,LuX,KovavisaruchL.SourcelocalizationusingTDOAandFDOAmeasurementsinthepresenceofreceiverlocationerrors:Analysisandsolution[J].IEEETrans.onSignalProcessing, 2007, 55(2): 684-696.

[3] 郭福成，樊昀. 双星时差频差联合定位方法及其误差分析[J]. 宇航学报，2008, 29(4):1381-1386.

[4] Huang YT, Benesty J, Elko GW, et al. Real-time passive source localization: A practical linear-correction least-squares approach [J]. IEEE Tran. on Speech and Audio Processing, 2001, 9(8): 943-956.

[5] Stein S. Algorithms for ambiguity function processing [J]. IEEE Trans. on Acoustics, Speech, and Signal Processing, 1981, 29(3):588-599.

[6] Stein S. Differential delay/doppler ML estimation with unknown signal [J]. IEEE Trans. on Signal Processing, 1993, 41(8): 2717-2719.

[7] Naghsh-Nilchi AR, Mathews VJ. An Efficient Algorithm for joint estimation of differential time delays and frequency offsets[C]∥Proceeding of JCASSP-92. 1992: 309-312.

[8] Ulman J, Geraniotis E. Wideband TDOA/FDOA processing using summation of short-time CAF’s [J]. IEEE Trans. on Signal Processing, 1999, 47(12): 3120-3193.

[9] Shin DC, Nikias CL. Estimation of frequency-delay of arrival (FDOA) using fourth-order statistics in unknown correlated gaussian noise sources [J]. IEEE Transactions on Signal Processing, 1994, 42(10):2771-2780.

[10]Dandawate AV, Giannakis GB. Differential delay-doppler estimation using eecond- and high-order ambiguity functions [J]. IEE Proc.-Radar Sonar Navig, 1993, 140(6):410-418.

[11]Weinstein E, Kletter D. Delay and doppler estimation by time-space partition of the array data [J]. IEEE Trans. on Acoustics, Speech, and Signal Processing, 1983, 31(6): 1523-1535.

A novel estimation method of TDOA and FDOA for pulse train signal

Xiao Xuebing, Guo Fucheng, Jiang Wenli

(School of Electronic Science and Engineering,National University of Defence Technology,Changsha 410073,Hunan,China)

Concerned with the character of multi-peak of CAF of pulse train and the heavy computation load, a new method for jointing estimation of TDOA and FDOA is proposed. Based on the relationship between the FDOA and the slope of TDOA, a sequence of TDOA is used to guide the searching range of TDOA and FDOA of CAF. The estimation method of TDOA and FDOA based on CAF is improved by the sparse character of pulse train in time domain. Theoretic derivation and simulation show that this approach can ascertain the ambiguity effectively as well as reduce the compute load without decreasing the estimation accuracy.

pulse train; TDOA; FDOA; CAF

国防科技重点实验室基金(9140C860304)

2014-07-05；2014-12-24修回。

肖学兵(1990-)，男，硕士研究生，主要研究方向为无源定位、雷达信号侦察。

TN974

A