开关磁阻电机转矩脉动与铜耗最小化控制研究

王喜莲,　许振亮,　王翠

(北京交通大学 电气工程学院,北京 100044)



开关磁阻电机转矩脉动与铜耗最小化控制研究

王喜莲,许振亮,王翠

(北京交通大学 电气工程学院,北京 100044)

摘要:针对开关磁阻电机(switched reluctance motor, SRM)的双凸极结构导致其运行时产生很强的转矩脉动现象,根据SRM非饱和特性下电感与角度关系曲线,提出一种基于指数函数的SRM转矩脉动与铜耗最小化转矩分配综合控制方法,该方法综合转矩计算式和查表法将参考转矩直接转化为参考电流,避免了对转矩的测量。与正弦转矩分配控制进行比较分析,在电机工作效率方面验证了该控制系统性能的优越性;提出将转矩脉动抑制作为主要优化对象,抑制定子绕组换相电流作为次级条件,利用加权函数实现转矩脉动抑制与运行效率的优化平衡方案。以一台3 kw的12/8极开关磁阻电机为控制对象,建立控制系统仿真模型,验证了方案的有效性。

关键词:转矩分配; 指数函数; 开关磁阻电机; 铜耗; 转矩脉动; 权重值

许振亮(1986—),男,硕士研究生,研究方向为开关磁阻电机及其控制；

王翠(1989—)，女，硕士研究生，研究方向为开关磁阻电机及其控制。

0引言

开关磁阻电机(switched reluctance motor, SRM)具有结构简单、成本低和可靠性高等优点,自20世纪80年代问世以来,得到了迅猛发展。随着科技发展,对电机驱动系统的转矩脉动、效率和噪声等指标要求越来越高,但开关磁阻电机自身双凸极结构的特点,导致转矩脉动和噪声大成为限制其发展的主要因素。为了使SRM产生恒定转矩和最小化转矩脉动,各国学者提出了多种控制方法,如PWM斩波调压控制[1]、直接转矩控制(direct torque control,DTC)[2]、电流双幅值斩波控制、自适应控制[3]、人工神经网络控制[4]等。这些控制方法在很大程度上降低了SRM的转矩脉动,但没有考虑电机运行效率的问题。如直接转矩控制方法,虽然其转矩脉动很小,但其开关管的开关规则执行起来很繁琐,高速时在换相阶段易出现转矩失控现象,运行效率很低[5]。转矩分配函数控制方法[6-7]有效地减小了转矩波动,但没有综合考虑运行效率、转矩——速度特性等优化指标。文献[8]提出了转矩波动与铜耗最小化的综合控制概念,并基于线性的、正弦的转矩分配函数以及考虑铜损及电流电压限制的优化转矩分配函数法进行了研究,有效地改善了系统性能。

本文提出基于指数函数的综合优化控制方案,同时考虑了SRM驱动系统的转矩脉动和运行效率问题,将转矩脉动作为主要考虑因素,将运行效率作为次要考虑因素。并在传统转矩分配控制的基础上进行改进,实现对转矩脉动和运行效率的优化处理。利用Matlab建立了基于查表模块的12/8极SRM的非线性动态仿真模型[9],给出了改进后的转矩分配控制方法,建立了换相重叠角与换相电流的数学关系。最后对传统转矩分配控制和改进的转矩分配控制都进行了仿真,仿真结果表明本文提出的方法可以实现开关磁阻电机的转矩脉动和铜耗的最小化,在运行效率方面与传统转矩分配控制相比具有很大的优势。

1开关磁阻电机的本体仿真模型

由于开关磁阻电机的磁路非线性以及存在相间耦合,导致其精确模型很难建立。本文建立其简化模型,并在建模过程中假设:IGBT的开通、关断均无过渡过程,电机各相对称,忽略相间电感,功率电路的工作方式采用斩双管,当半桥上下桥臂的IGBT均处于导通时,其电压方程为

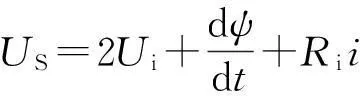
(1)

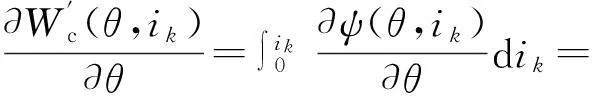
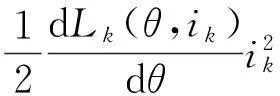
(2)

针对一台3相12/8极开关磁阻电机,借助JMAG-11.0软件进行电磁有限元分析,该电机的铁心材料为DW540-50,叠压系数为0.95,定子外径为155 mm,定子内径为90 mm,定子绕组电阻为1.4 Ω,额定功率3 kW。通过有限元分析得到电机每相磁链ψk(θ,ik)的离散数据,对磁链数据ψk(θ,ik)进行逐段3次埃米特反向插值来得到ik(θ,ψk)离散数据,如图1所示。

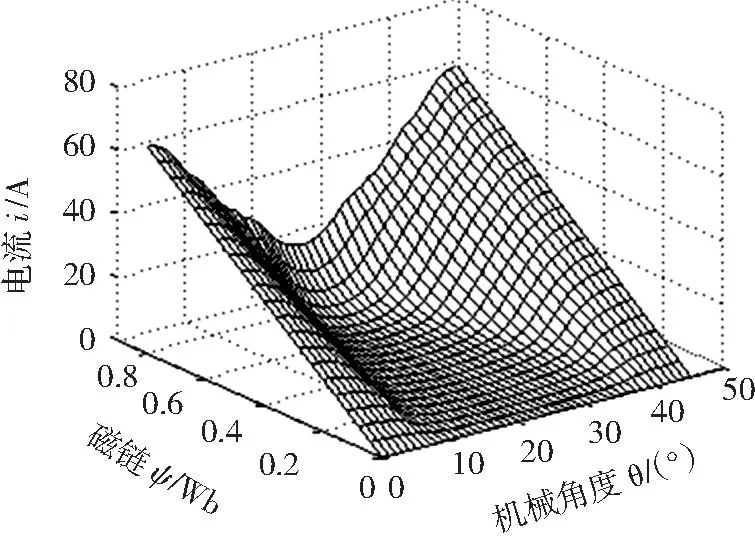
图1　SRM的电流曲线

有限元分析同时得到了转矩Tk(θ,ik)的离散数据,如图2所示。

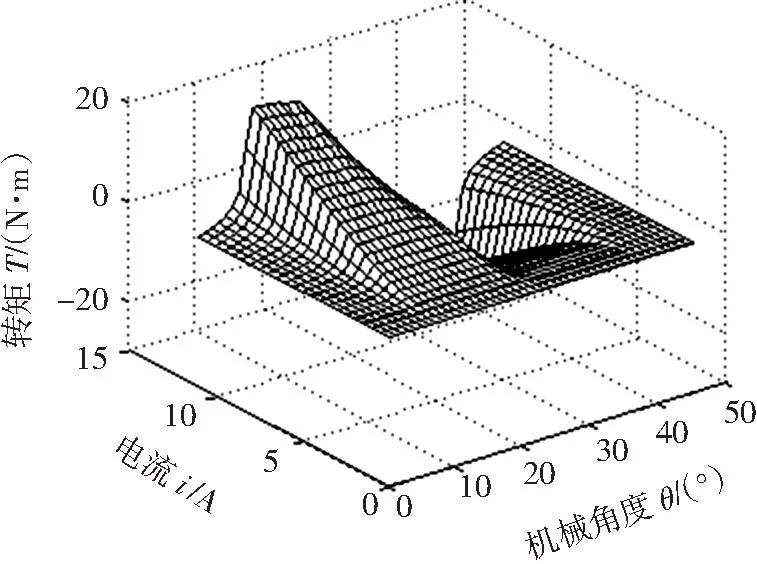
图2　SRM的转矩曲线

结合式(1)和式(2)利用Matlab/SIMULINK的查表模块,建立开关磁阻电机的仿真模型,图3为三相开关磁阻电机中A相的仿真模型。

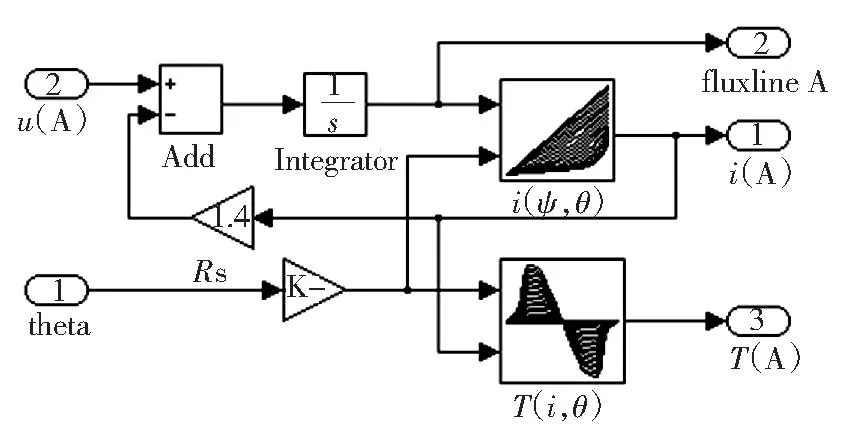
图3　SRM非线性磁链仿真模型

2转矩分配函数(TSF)控制理论

2.1　SRM的转矩表达式分析

由于开关磁阻电机的双凸极结构和磁路易饱和的特点,电感Lk不仅与转子位置角θ有关,而且与定子绕组相电流ik有关,图4为绕组电流分别为1 A,2 A,3 A,4 A,5 A,6 A和7 A时所对应的电感值。

图4　SRM的电感曲线

由图4可以看出,绕组电流值为1 A,2 A,3 A和4 A时的电感曲线几乎都叠加在一起,在绕组电流超过5A后电感值明显下降,说明此时电机进入磁路饱和状态,最大差值不超过0.05 H。

图5为绕组电流分别为1 A,2 A,3 A,4 A,5 A,5.5 A和10 A时所对应的dLi(θ,ik)/dθ波形。

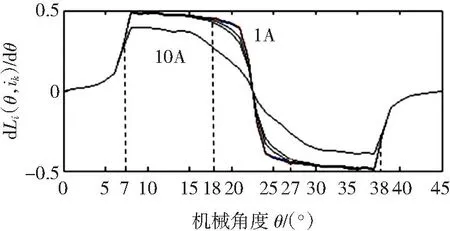
图5　电感关于转子位置角的微分曲线

由图5可见电流小于5.5 A时各dLi(θ,ik)/dθ波形基本叠加在一起,只有在18°≤θ≤27°时各波形差值较大。电流为10 A时磁路饱和较严重,但在转子位置角度低于7°时,其波形未出现明显饱和现象。由于转矩分配控制的特点,一般在每一相初始阶段(定子齿与转子槽中心线对齐附近)就会被分配较大的转矩,因此每一相只有在初始阶段才会有较大的换相电流,而图5所示,在每一相的初始阶段是不易出现饱和的。因此可忽略在SRM中的磁路饱和影响,将图5中的曲线簇用一条曲线表示。对1 A,2 A,3 A,4 A,5 A和5.5 A时的dLi(θ,ik)/dθ波形进行求平均值计算,其平均值波形如图6所示。

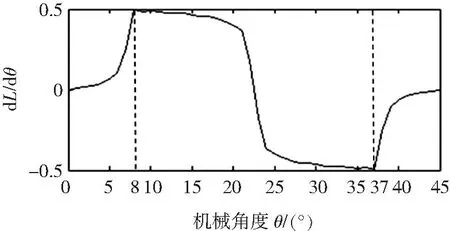
图6电感平均值关于转子位置角的微分曲线

Fig. 6Average inductance derivative

curves on rotor angle

在上述情况下,式(2)可以改写成[10]

(3)

2.2　基于指数函数的转矩分配函数(TSF)

通过转矩分配函数将合成转矩Ts分解为对应于每相的独立转矩,常用的转矩分配函数有线性和一次正弦函数两种,其中基于正弦函数的转矩分配波形如图7所示。

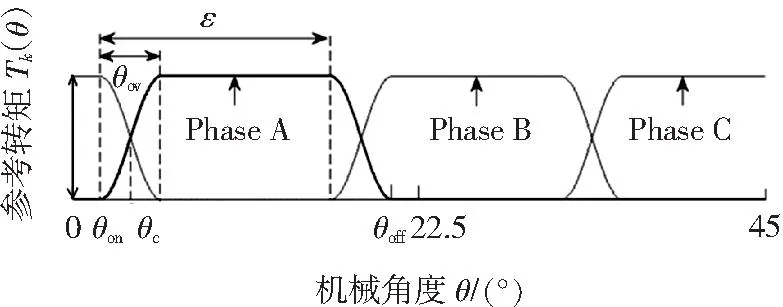
图7　基于正弦函数的理想转矩分配波形

Fig. 7Ideal torque distribution waveform based

on sinusoidal function

图7中θov为换相重叠角,θon为A相开通角,θoff为A相关断角,θc为换相时相邻相参考转矩相等时的角度,ε为相邻相间的相移角度。

由式(2)可知,开关磁阻电机的转矩波形应与图6类似,在0°到8°时的转矩波形与线性及一次正弦函数波形相差较大,如果采用线性或正弦函数,则在开通的初期导通相就被分配到很大的转矩,这将增大换相时定子绕组电流峰值,而这些多出的尖峰电流无疑将增大电机的铜耗。因此本文提出基于指数函数的综合考虑转矩波动及铜耗最小化的转矩分配函数法。本文利用指数函数组建转矩分配函数,其转矩分配波形如图8所示。

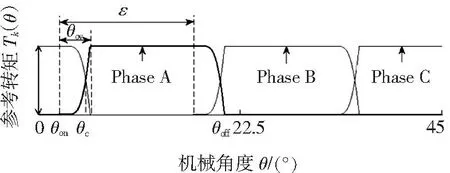
图8　基于指数函数的理想转矩分配波形

Fig. 8Ideal torque distribution waveform based

on exponential function

根据转矩分配函数,每相参考转矩的函数定义为

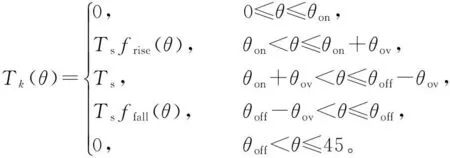
(4)

其中frise(θ)和ffall(θ)分别为

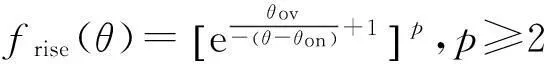
(5)

(6)

由图8可知,式(5)和式(6)中的p取值越大,每一相初始阶段被分配的转矩越小,关断阶段被分配的转矩越大,进而每相初始阶段电流值越小,关断阶段电流越大。基于转矩分配函数的三相SRM控制系统方框图如图9所示。

图9　SRM的转矩分配控制系统方框图

3转矩分配控制的运行效率优化

采用转矩分配控制的主要目的是减小转矩脉动,其中转矩分配函数的可变量包括θov,θon和θoff。铜耗作为次级考虑因素,铜耗直接影响到电机的运行效率。转矩分配函数以及可变量的选择直接影响转矩脉动和各相参考峰值电流的大小。其中,对应采用正弦函数的转矩分配理论中θc,θov,θon和θoff满足式(7)和式(8)的关系。

θoff-θon=θov+ε，

(7)

θov=2(θoff-θc-ε)。

(8)

而对应采用指数函数的转矩分配理论中θov,θon和θoff只满足式(7)。由于SRM的一个运行周期包括3个ε,因此ε可由式(9)来确定。

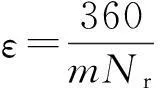
(9)

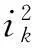
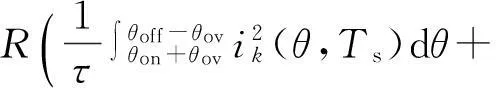
(10)

对于输出合成转矩已经确定的情况,由式(2)和图6可知,铜耗的差异主要取决于换相阶段两个相邻相电流值之和,因此以式(10)中的第二项作为优化对象,对于第二项中的积分部分可以定义一个表达式为

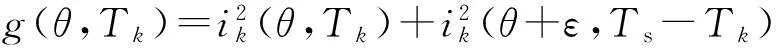
(11)

将式(11)与式(3)联立,可进一步得出

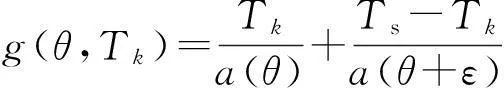
(12)

对于特定电机而言,a(θ)已固定不变,由式(12)和式(10)可知,θov越小,式(10)中的第二项越小,但定子绕组为感性,存在充放电时间,电机转子旋转时,θov不可能为0,因此需要确定最小重叠角θovmin。若忽略绕组的电阻Ri和IGBT管压降Ui,式(1)可以变形为

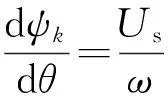
(13)

理论最小重叠角θovmin可表示为

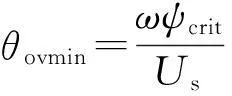
(14)

其中ψcrit为在直流电压US作用下,在θc和θc+ε范围内能产生参考转矩TS所需的磁链。由式(3)可知,式(14)还可以进一步变形为

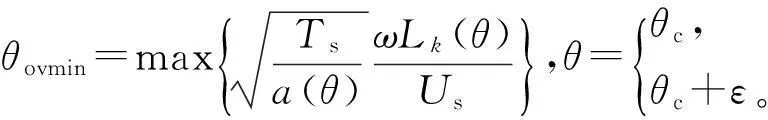
(15)

由图6,图8和式(3)可知,在绕组电流相同情况下,相邻两相所产生的转矩在转子位置角θc处应相同,因此得到确定θc的公式为

a(θ)=a(θ+ε) 。

(16)

4TSF综合控制系统仿真分析

对于该12/8极开关磁阻电机,根据式(16)和图6,通过SIMULINK建计算模型,得到θc为6.78°。设定直流电源电压US为280 V,转速为200 r/min,合成参考转矩Ts为2.6 N·m。本文对基于正弦函数和指数函数的两种转矩分配控制方法进行了仿真,当采用一次正弦函数的转矩分配控制策略,由式(8)和式(15)可计算出其θovmax和θovmin分别为1.45°和0.11°,当采用指数函数的转矩分配控制策略,由式(7)和式(15)可计算出其θovmax和θovmin分别为7.5°和0.11°,但为了进行比较,其换相重叠角的取值范围也定为0.11°到1.45°之间。

为了对比基于正弦函数和指数函数的两种转矩分配控制方法在电机运行效率方面的差别,将在不同换相重叠角下通过仿真得到的换相区域相邻相电流平方和的积分的标幺值数据建立成曲线,基数为采用正弦函数的转矩分配控制策略,且θov为1.45°时换相区域相邻相电流平方和的积分值,具体如图10所示。其中带有方块标识的曲线为采用指数函数的转矩分配控制策略,带有三角标识的曲线为采用正弦函数的转矩分配控制策略。

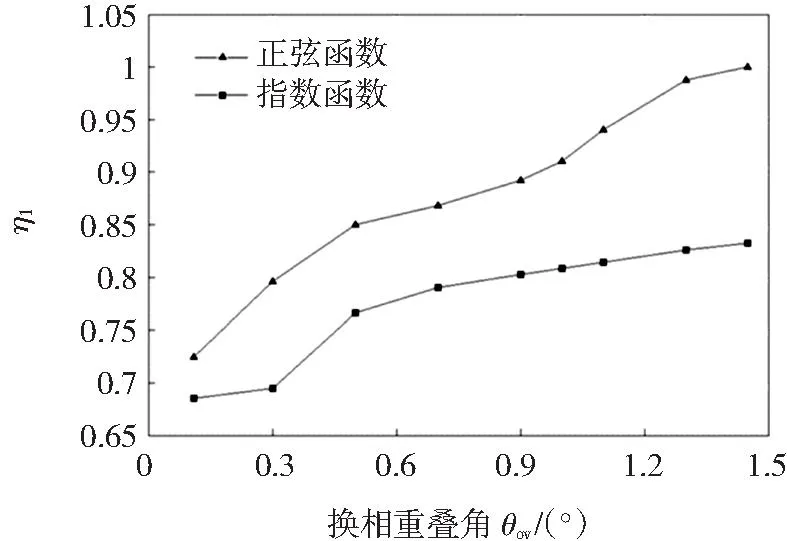
图10　η1与换相重叠角的关系曲线

其中,η1为换相区域相邻相电流平方和的积分的标幺值。从图10可以看出,当采用基于指数函数的转矩分配控制策略时,η1明显减小。并且当θov越大,换相重叠区导通相的峰值电流越小,这是由于换相重叠区增大,各相参考转矩的上升斜率减小,从而导通相的电流上升斜率也减小,但这却导致了换相区域相邻相电流平方和的积分值的增大。

此外,针对基于指数函数的转矩分配控制策略,其最大换相重叠角θovmax可达到7.5°,为了达到运行效率和转矩脉动的平衡,本文引入了加权函数为

B(θov)=0.3η(θov)+0.7A(θov)。

(17)

其中,η(θov)为换相区域相邻相电流平方和的积分的标幺值,基数为θov是7.5°时换相区域相邻相电流平方和的积分值。A(θov)为转矩最大值与最小值之差的标幺值,基数为θov是0.11°时转矩最大值与最小值之差。式中权重值的选取主要取决于对电机运行效率和转矩脉动的侧重程度,本文将转矩脉动抑制作为主要条件,将电机运行效率作为次要条件,因此将其权重值分别取为0.7和0.3。

η(θov)的曲线如图11(a)所示,A(θov)的曲线如图11(b)所示,B(θov)的波形如图11(c)所示。

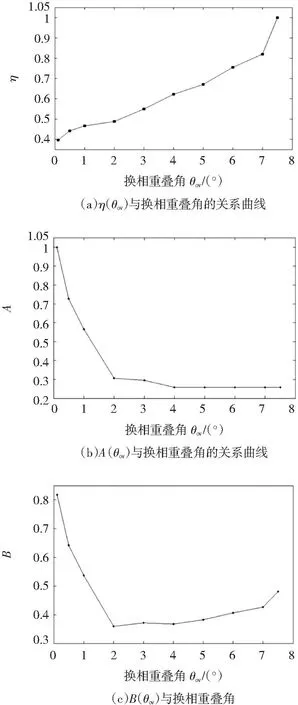
图11　η(θov)、A(θov)和B(θov)与换相重叠角的关系曲线

由图11(b)可知,由于电流闭环中滞回比较器的作用,一相单独导通时转矩波形存在振荡,在换相重叠角θov大于4°后,换相阶段产生的转矩脉动低于单相导通阶段转矩的振荡,因此A(θov)恒定为0.25。由图11(c)可知,当θov为2°时,B(θov)达到最小值,即为0.36。

当θov为2°,转速为200 r/min,负载转矩为2.6 N·m时,该开关磁阻电机的合成转矩、磁链和定子绕组电流的仿真波形如图12(a)所示。当θov等于2°,转速为1 000 r/min,转矩为1.8 N·m时,该开关磁阻电机的合成转矩、磁链和绕组电流的仿真波形如图12(b)所示。

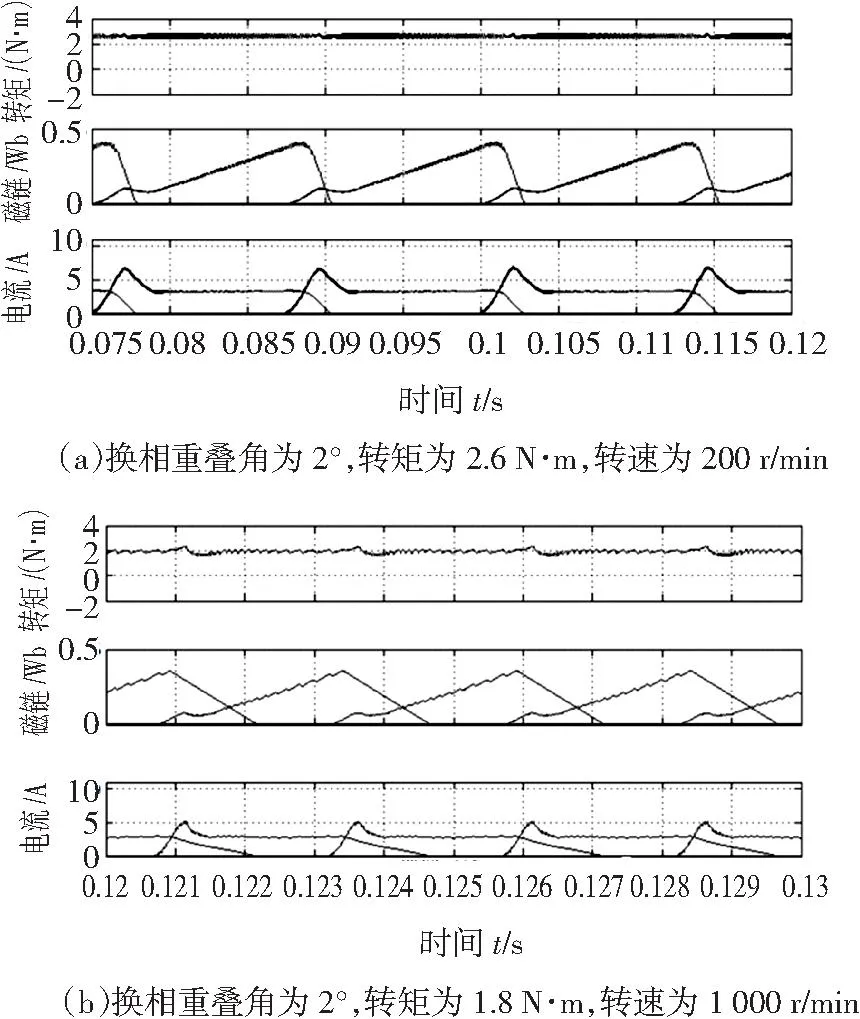
图12　SRM驱动系统的仿真结果

通过图12(a)可以看出,在低速运行时,开关磁阻电机的转矩脉动很低,克服了开关磁阻电机低速运行时步进状态明显的缺点,而图12(b)则表明开关磁阻电机在1 000 r/min时,运行状态稳定,转矩脉动略微增大,证明这种控制策略具有较好的转矩——速度特性,即电机在较高速运行时转矩脉动不出现大的变化。因此,由图10和图12可知基于指数函数的综合转矩波动与铜耗最小化的转矩分配控制策略在电机运行效率提高和转矩脉动抑制方面的有效性。

5结论

基于指数函数综合转矩波动与铜耗最小化的转矩分配控制方法,针对3 kW 12/8极开关磁阻电机进行仿真分析,通过转矩表达式和查表模块,将参考转矩直接转化为参考电流,从而不必检测电机的输出转矩。与传统正弦转矩分配策略相比,该策略在电机运行效率方面具有优势。从抑制转矩脉动和提高电机运行效率两个方面进一步综合考虑,利用加权函数达到优化平衡。结果表明本文提出的控制策略有效的提高了电机运行效率,降低了转矩脉动。同时,仿真结果对开关磁阻电机调速系统的设计具有很好的参考价值。

参 考 文 献:

[1]HUSAIN I, EHSANI M. Torque ripple minimization in switched reluctance motor drives by PWM current control[J]. IEEE Transactions on Power Electronics, 1996, 11 (1):83-88.

[2]漆汉宏, 张婷婷, 李珍国, 等.基于DITC的开关磁阻电机转矩脉动最小化研究[J].电工技术学报, 2007,22(7):136-140.

QI Hanhong, ZHANG Tingting, LI Zhenguo, et al. SRM torque ripple minimization based on direct instantaneous torque control [J]. Transactions of China Electrotechnical Society, 2007, 22(7):136-140.

[3]OMEKANDA A M. A new technique for multi-mensional performance optimization of switched reluctance motors for vehicle propulsion [J]. IEEE Transactions on Industry Applications, 2003, 39(3):672-676.

[4]夏长亮, 陈自然, 李斌.基于RBF神经网络的开关磁阻电机瞬时转矩控制[J].中国电机工程学报, 2006,26(19):127-132.

XIA CL, CHEN ZR, LI B. Instantaneous torque control of switched reluctance motors based on RBF neural network [J]. Proceedings of the CSEE, 2006, 26(19): 127-132.

[5]许爱德, 樊印海, 李自强.空间电压矢量下SRM转矩脉动最小化[J].电机与控制学报, 2010, 14(1):35-40.

XU Aide,FAN Yinhai,LI Ziqiang. SRM torque ripple minimization based on space voltage vector [J]. Electric Machines and Control, 2010, 14(1):35-40.

[6]ILIC-SPONG M, MILLER T J E, MACMINN S R, et al. In-stantaneous torque control of electric motor drives[J]. IEEE Transactionson Power Electronics, 1987, 2(1):55-61.

[7]XUE XD, CHENG KWE, HO SL. Optimization and evaluation of torque-Sharing functions for torque ripple minimization in switched reluctance motor drives[J]. IEEE Transactions on Power Electronic, 2009, 24(9): 2076-2090.

[8]VLADAN P, VUJICIC. Minimization of torque ripple and copper losses in switched reluctance drive [J]. IEEE Transactions on Power Electronics, 2012, 27(1):388-399.

[9]刘闯,严利,严加根,等.开关磁阻电机非线性磁参数建模方法[J].南京航空航天大学学报,2007, 39(6): 706-710.

LIU Chuang, YAN Li, YAN Jiagen, et al. Nonlinear magnetization data modeling method based on MATLAB/SIMULINK of switched reluctance motor system [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(6):706-710.

[10]PAN J F, NORBERT C Cheung, YU Zou. An improved force distribution function for linear switched reluctance motor on force ripple minimization with nonlinear inductance modeling [J]. IEEE Transactions on Magnetics, 2012, 48(11):3064-3067.

(编辑：刘琳琳)

Torque ripple and copper losses minimization control study of switched reluctance motor

WANG Xi-lian,XU Zhen-liang,WANG Cui

(School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract:Torque-ripple of switched reluctance motor (SRM) is inevitable for its double saliency construction and switch power supply. To minimize the torque-ripple, according to unsaturation inductance-angle characteristics curve of the SRM, a torque distribution synthesis control method based on exponential function to decrease SRM torque ripple and copper losses was proposed. The reference torque was directly translated into the reference current using the torque figure and lookup table method to avoid the torque measure. Meanwhile, the proposed method was compared with the traditional sinusoidal torque distribution control method. The results show its superiority of the operational efficiency. The optimal balance scheme employing weighting function of torque ripple minimization and operational efficiency was proposed by setting torque ripple minimization as the major optimal object, reducing the stator winding commutation current as a secondary condition. The control system simulation model of a 3kw 12/8 poles switched reluctance motor was built to verify the validity of the proposed method.

Keywords:torque-sharing function; exponential function; switched reluctance motor; copper losses; torque ripple; value weighted

通讯作者:王喜莲

作者简介:王喜莲(1974—),女,教授,研究方向为开关磁阻电机、无轴承电机及其控制；

基金项目：财政部、教育部基本科研业务费(2014JBM111)；国家自然科学基金(50907004)

收稿日期:2013-12-06

中图分类号:TM 352

文献标志码:A

文章编号:1007-449X(2015)07-0052-06

DOI:10.15938/j.emc.2015.07.008