基于LM算法优化的RBF网络学生体质综合评价模型

2015-03-16李革

河池学院学报 2015年2期

李革

(柳州职业技术学院公共基础部，广西柳州 545006)

体质的好、坏对大学生的学习和工作都会产生影响，而体质是由人体形态结构、生理机能、心里因素以及运动能力等各要素组成的一个综合概念，因此，对大学生体质进行评价，是一项繁琐且复杂的工作。很多学者针对大学生体质综合评价问题进行了研究，旨在寻找一种有效和准确的综合评价学生体质的方法。

文献［1］针对体质综合评价中评价指标过于复杂的问题，引入权重概念对评价指标进行分级，最后利用层次分析法对学生体质进行综合评价;文献［2］利用层次分析法合理地确定各指标权重，建立灰色关联度综合评价模型;文献［3］利用主成分分析法对反映学生耐力素质和心肺功能的指标进行综合评价，从而反映学生的体质状况;文献［4］采用当前流行的BP神经网络算法建立了一种体质综合评价模型。以上方法对体质进行综合评价都取得了一定的效果，但准确率不够理想。本文借鉴文献［1－4］的思想，利用径向基函数(Radial Basis Function，简称RBF)神经网络具有良好非线性逼近能力的特点，采用Levenberg－Marquardt(简称LM)算法优化RBF神经网络权值，构造一个大学生体质综合评价模型，以期能客观、准确的反映大学生的体质状况，从而能够有针对性的引导学生进行锻炼，增强学生的体质，为工作和生活打下良好的基础。

1 LM算法优化的RBF神经网络模型

1.1 RBF神经网络概述

RBF神经网络［5］是一种前馈型网络，该网络性能优良，具有全局逼近能力。通过选择合适的核函数，RBF神经网络可以按指定的精度逼近任意的非线性函数，泛化能力强。RBF神经网络拓扑结构简单，基本的RBF网络结构包含三个层，分别为输入层、隐藏层和输出层，每个层上布满了神经元，不同层之间通过权值来连接各自的神经元。RBF神经网络的核函数和训练方法有很多种，它们各有优、缺点。本文采用高斯函数作为核函数，采用梯度下降法作为网络的训练方法。由于采用梯度下降法作为RBF神经网络的训练方法，此时网络存在训练时间过长且容易陷入早熟。为了能减少RBF神经网络的学习时间，避免陷入早熟的问题，引入LM算法对RBF神经网络的权值进行优化，以此提升RBF网络的性能。

1.2 LM优化算法概述

LM算法［6］是一种优化算法，它能对大规模的参数进行优化处理。该方法是高斯—牛顿算法和梯度下降法的结合，因此该方法具有高斯—牛顿算法的局部收敛性，又能利用梯度下降法对全局展开搜索。LM算法采用近似二阶求导，因此它比梯度下降法的运算速度快。LM算法基于以下原理［6］:

设W(k)表示第k次迭代的权值和阈值组成的解向量，通过以下指定的规则进行迭代求解:

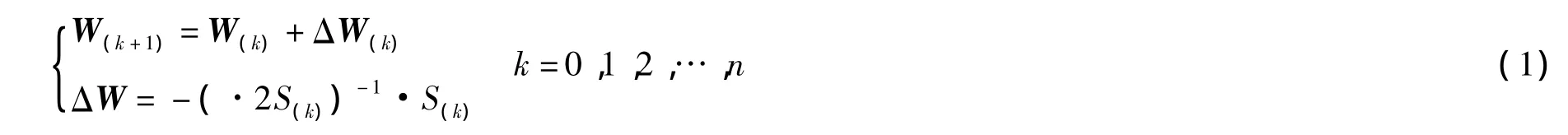
其中，S(k)为误差指标函数，与它对应的Hessian矩阵和梯度向量分别为·S(k)和·S(k)。

高斯—牛顿算法采用最小二乘法对函数的解进行估计，因而其误差指标函数可以用下式表示:

其中，ei(x)为误差(i=1，2，…，N);N是输出的向量维数。此时，算法第k次计算的ΔW可以表示为:

其中，J是S的雅可比矩阵。

作为一种改进的高斯—牛顿算法，LM算法的形式可以表示为:

其中，μ称为阻尼系数，它通常为指定的常数，且μ＞0，I是单位矩阵。

从公式(5)中可以看出，作为高斯—牛顿法和梯度下降法的结合体，当μ=0时，算法就转变为高斯—牛顿法;当μ趋向于一个很大的值时，算法可以近似认为是梯度下降法。当阻尼系数μ足够大的时候，总可以保证［JT(x)J(x)+μI］－1可逆。在实际的求解过程中，μ是一个动态的参数，本文实验部分所用LM算法的阻尼μ=JT(x)e(x)。

1.3 基于LM算法优化的RBF神经网络

LM算法具有很好的泛化能力。利用LM算法优化RBF神经网络权值的具体步骤如下［6］:

step1:初始化RBF神经网络的权值和阈值，并设定训练的误差值ε以及LM算法的阻尼系数μ以及微调系数 β，并令k=0;

step2:计算RBF神经网络的输出，同时按公式(2)和(4)分别计算网络的误差指标S(k)以及ΔW;

step3:如果S(k)＜ε则算法停止，否则算法进一步迭代，计算X(k+1)及其误差指标S(k+1);

教师在教学过程中一定要要求学生完全根据想象中的练习进行实践，这样才能达到提升练琴效率的目的，并且能够在更少的练习情况下能更高校的巩固加深对音乐片段的学习。同时，在想象练习时已一定要具体，具体到每一个音怎么谈，且不能有错，这样才能保证在实践时精准无误的演奏。实践时一旦发现有误，一定要及时更正相应的想象，务必从意识上更正错误，否则对于错误的想象大脑在加深印象后也会更难修正。在钢琴演奏中，教师会发现很多学生会在同一个地方不停的犯错，这就是因为学生对错误的演奏没有从大脑意识里及时更改并加深对正确演奏的想象。

step4:如果S(k+1)＜S(k)，则令k=k+1，μ =μ/β，跳转到 step2，否则不做任何更新，μ = μβ，算法跳转到step3。

2 大学生体质综合评价指标的选取

体质的综合评价是一个富有挑战性的课题，主要的原因是人体结构复杂，而反映人的体质好坏，则是一系列综合因素影响的结果。一般而言，体质综合评价因素主要由人体自身的形态、身体的机能、人体的运动能力以及人的心里素质等构成。影响人体综合评价的每一个因素又由若干个指标来体现，这些评价指标相互联系、相互制约。对大学生体质进行综合评价，必须要选择科学合理的评价指标。对影响大学生体质的评价指标必须遵循科学性和可行性的原则进行选取［7］:(1)科学性是指选取的指标必须符合人体生长的基本规律，必须符合医学和体育的学科理论;(2)可行性是指所选取的指标应该简单化和规范化，便于测量，易于操作。

在借鉴了文献［1－4］所采用的评价指标后，本文依据现行的《大学生体质健康标准》，根据科学性和可行性的原则，经过充分考虑后，选择身体形态、运动能力和身体技能这三个因素构建体质的综合评价体系。本文构建的体质综合评价体系见表1［8］。

从表1中可以看到，身体形态因素主要采用克托莱指数来体现，其计算公式为:克托莱指标=体重(kg)/身高(cm)×1 000，该指标能间接反映出人体胸围的宽度和厚度，从而反映出人体形态的发育情况。人体自身的肺活量与体重的比值称为肺活量体重指数，用该指标来反映人体的机能状况，它主要用来做一个定量的比较分析，用于比较不同性别、年龄的个体和群体之间的差别。人体机能的另一个重要指标是台阶试验指标，它主要通过持续的、有节律的登台阶运动所用的时间和人体恢复平静后测量的脉搏次数的比值来反映人体心血管系统机能的状况，该指标越高则表明人体的心血管系统机能越好，通过该指标还可以间接的反映人体的耐力。在本文设定的指标体系里，主要通过50米短跑和立定跳远分别体现人体运动的速度和灵敏度，而人体静力性力量主要通过引体向上来体现，这三个指标综合的体现了人体的运动能力。

表1 大学生体质综合评价指标

3 评价模型的具体应用

3.1 数据的采集

国家要求各高校每年都要进行体质测试，为了能更好的说明问题，我们对数据进行了挑选，选取某学院2012～2014年大一和大二的男生共6 000名的体质测试成绩来进行网络的训练和测试，所挑选出来的数据见表2。

表2 部分大学生体质测试原始数据

3.2 模型的训练

公式(5)中，同组数据中的最大最小值分别用max(x)和min(x)来表示，归一化后的数据用表示。归一化后的数据如表3所示。

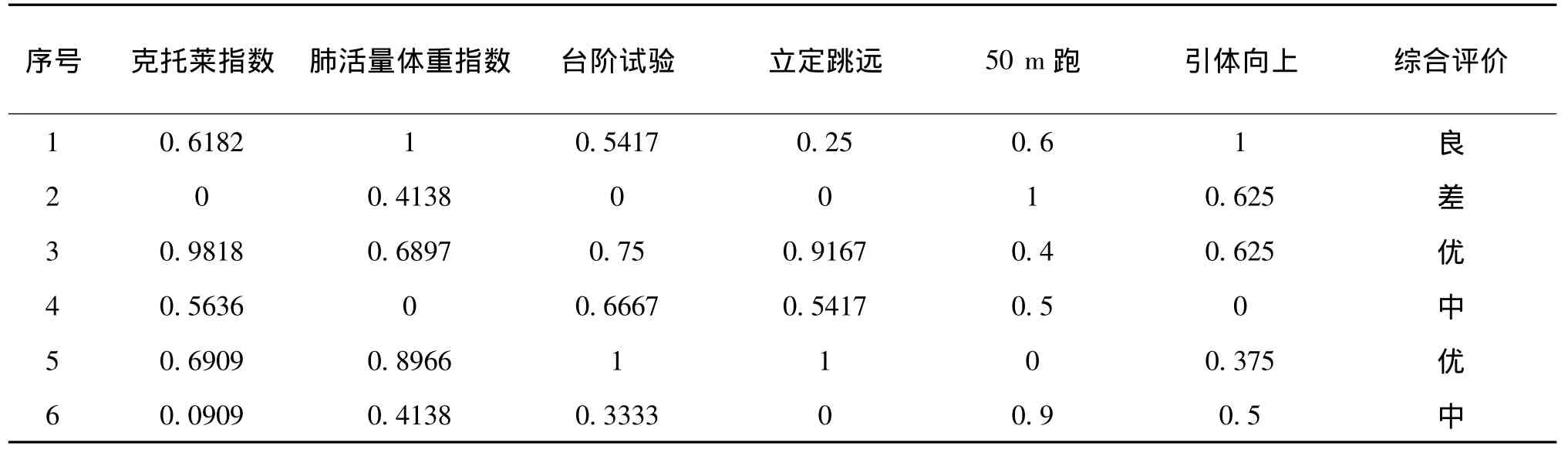
表3 大学生体质测试归一化数据

根据本文设定的体质综合评价指标可知RBF网络的输入层为6。本例中，网络的输出目标是优、良、中、差四个等级，为了便于网络处理必须对输出的目标进行转换，见表4所示。

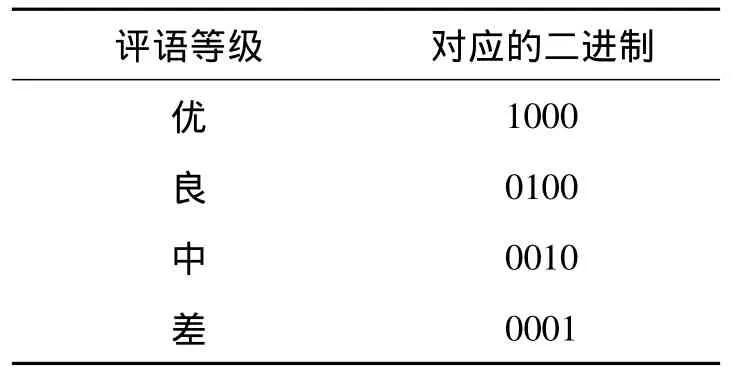
表4 转换的评语等级对照表

随机选取5 000笔数据作为训练的样本，剩余的1 000笔数据作测试。本实验硬件环境为酷睿i3 2.2 GHz CPU，4 G内存，在win7 64位系统下，采用Matlab7编程实现。通过训练，经过LM算法优化的RBF神经网络综合评价模型的输出结果接近值，准确率达98.1%，证明该评价模型可信度较高。为了证明经过LM算法优化的RBF神经网络模型(简称LMRBF)比没有经过优化的RBF神经网络模型(简称RBF)和文献［4］所采用的BP神经网络模型(简称BP)优秀，我们还做了对比实验，实验结果如图1所示。

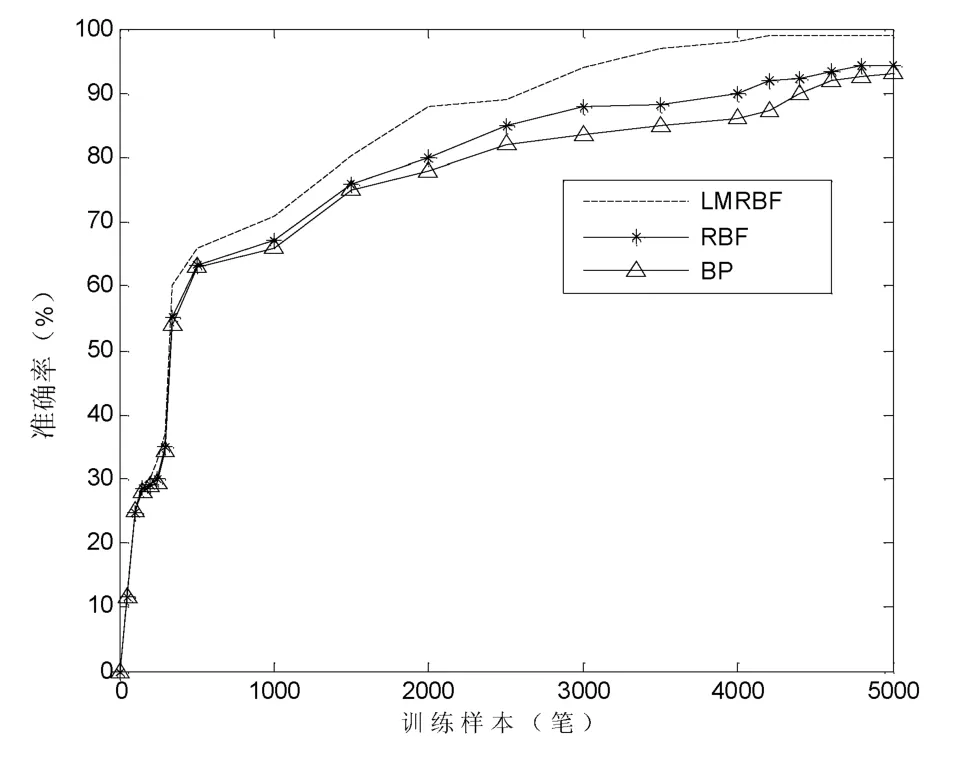
图1 三种算法准确率的比较

3.3 结果分析

从图1我们可以看到，三种算法在前1 000笔训练数据的时候，由于样本量不大，三种算法的准确率都相差不多，但LMRBF算法的准确率一直都比另外两种算法要高，这证明，LM算法起到了很好的优化作用。通过对2 000笔数据的训练，LMRBF算法的准确率提升很快，这说明训练样本的数量在很大程度上决定了模型所能获取的精度，也就是说，必须要保证足够的训练样本才能保证模型的准确率。从图1的结果可以看到，LMRBF算法准确率高，可以满足实际的应用要求。