脉冲离散切换系统的指数稳定性

韦佳，罗日才

(1.贵州师范大学附属中学，贵州 贵阳 550025;2.河池学院 计算机与信息工程学院，广西 宜州 546300)

脉冲切换系统是脉冲混杂系统里最重要的一类，至今仍然处于发展阶段。1998年Lakshmikantham和Liu最先提出脉冲混杂系统概念，并利用Lyapunov函数和比较原理讨论该系统的稳定性［1］。2003年Liu等利用Lyapunov函数方法和Riccati不等式建立一类拟线性脉冲混杂系统稳定和鲁棒稳定的充分条件［2］。国内专家近几年来也对脉冲混杂系统和脉冲切换系统进行研究，并取得了阶段性的成果［3-9］。

本文研究了如下线性脉冲离散切换系统

其中，X(k)∈Rn为状态变量，i(τ)∶R+→I={1，2，…，m}，τ∈{0}∪N，Δx(k+1)=x(k+1)-x(k)=Bkx(k)⇒k=kτ，x(k+1)=(I+Bk)x(k).

在研究了线性脉冲离散切换系统的指数稳定的基础上，本文还考虑了不确定性对此系统稳定的影响，研究了如下具有非线性不确定扰动项的脉冲离散切换系统

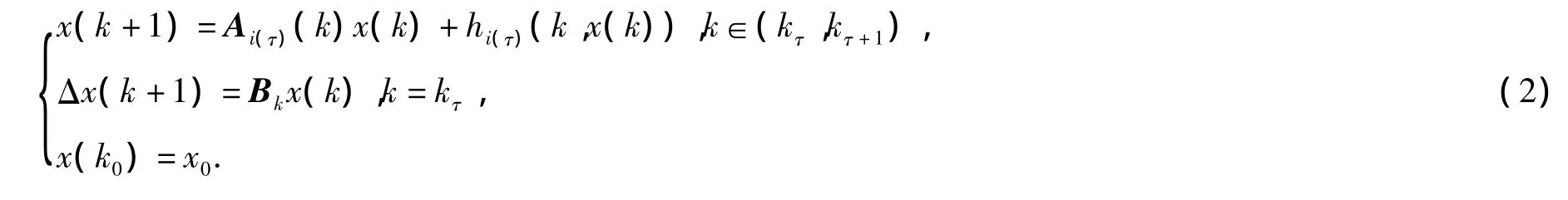
其中，hi(τ)(k，x(k))表示非线性不确定扰动项，其它符号含义与系统(1)相同。

假设脉冲切换系统(1)、(2)的解为x(t)，根据有关文献，我们给出如下定义:

定义1［10］:若∃α ＞0，∀ε ＞0，∃δ(ε)＞0，∀k0≥0，当‖x0‖＜ δ时，对所有的k≥k0，有‖x(k)‖ ＜εe-α(k-k0)‖x0‖，则称脉冲离散切换系统的零解指数稳定。

定义 2［11］:A=(aij)n×n，x=(x1，x2，…，xn)T，y=(y1，y2，…，yn)T∈Rn，|A|=，如果 x≤y，当且仅当xi≤yi(i=1，2，…，n)。

定义 3［12］:记S={kτ，iτ)|τ∈N+，iτ∈{1，2，…，m}}表示切换模式，m∈N+是有限数，{kτ}是任一无穷数列，称为切换序列。在切换模式和脉冲模式作用下构成的系统，其发生切换的同时也发生脉冲，如图1所示。

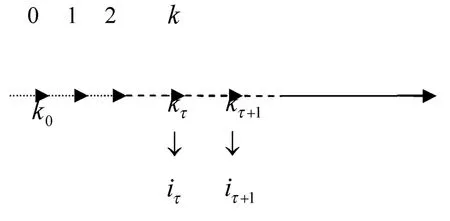
图1 切换序列图

另外，我们给出如下假设:

H1:系统(1)、(2)中各系统的整体解存在唯一。

H2:为了避免整个系统频繁切换引起的颤动，要求系统在有限时间内切换的次数是有限的。

H3:系统在每个切换时刻产生脉冲，并且当系统切换至同一个子系统时，所受的脉冲作用是一样的。

H4:序列{kτ}，满足:kτ∈N，k0=0 ＜k1＜k2＜… ＜kτ＜…，且kτ+1-kτ≥2，

因此，kτ≥kτ-1+2≥kτ-2+4≥…≥k0+2τ=2τ.

H5:对于任意i(τ)∈N，都存在某个有界常数 σi(τ)＞0，使得‖hi(τ)‖≤σi(τ)‖x‖成立，i(τ)∈N。

1 引理

引理1［13］:当X，Y及Σ∈Σ*为适当维数矩阵，‖Σ‖≤1，对于任意ε＞0，则下列不等式成立:

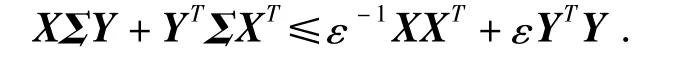
引理 2［13］:X∈Rn×n为正定矩阵，Q∈Rn×n为对称矩阵。对于∀x∈Rn，下列不等式成立:

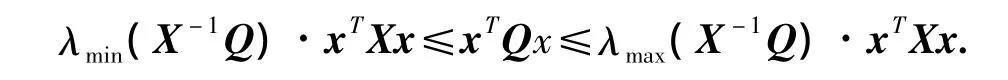
引理 3［14］:如果存在一个正定函数V(x)∶Rn→R+，∃β ＞0，满足

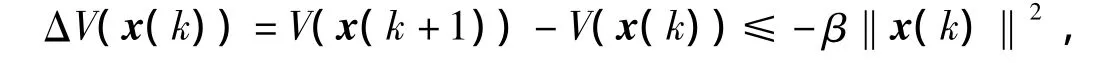
则系统是渐近稳定的。

引理4［15］:对于任意常对称矩阵 M∈Rn×n，M=MT＞0，标量s∈Z+/{0}，向量函数 W∶［0，s］→Rn，我们有

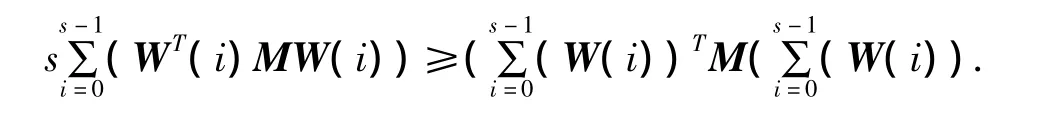
引理5(Schur补定理)［16］:设A，B，C是适当维数的矩阵，那么下面三式等价:

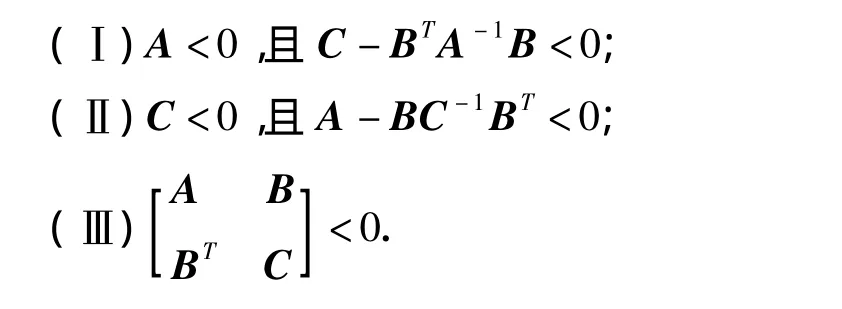
2 主要结论

2.1 线性脉冲离散切换系统

定理2.1 假设 H4 成立，对于系统(1)，如果存在一个常数 α ＞0，对于任意k∈(kτ，kτ+1］，τ∈N，使得

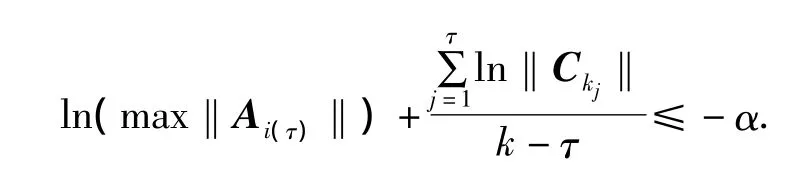
成立，则系统(1)为指数稳定的。

证明:对于任意k∈(kτ，kτ+1］，τ∈N，我们得到

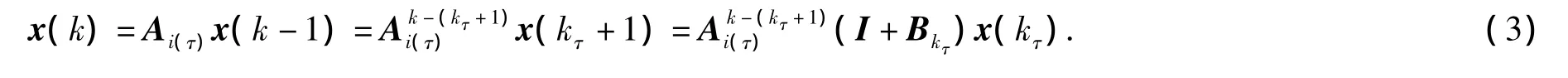
令 Ckτ=I+Bkτ，则

由式(3)和式(4)可以得到

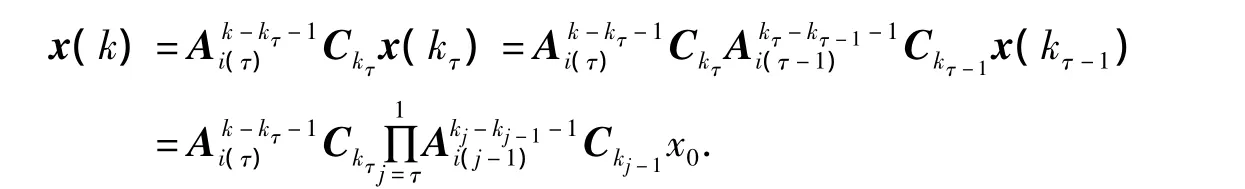
两边取范数，得到(取k0=0)

根据假设 H1，得到kτ≥kτ-1+2≥kτ-2+4≥…≥k0+2τ=2τ.因此，对于任意k∈(kτ，kτ+1］，得到‖x(k)‖≤e-α(k-τ)‖x0‖ ＜e-ατ‖x0‖.根据定义，显然系统(1)的状态轨线是指数稳定的。

接下来讨论非线性不确定扰动项的脉冲离散切换系统的指数稳定性。

2.2 非线性脉冲离散切换系统

定理2.2 假设 H5 成立，如果存在正定矩阵 Pj∈Rn×n和常数 εj＞0，使得∑∞j=0lnγj=-∞.成立，这里

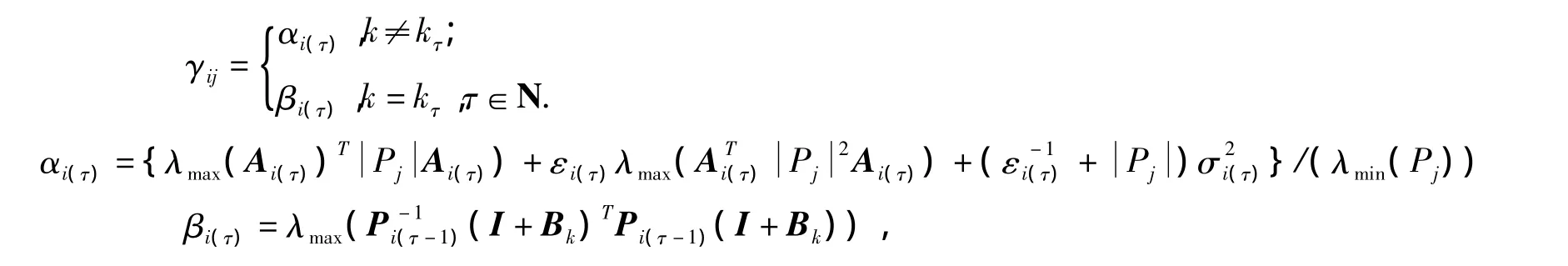
此时，系统(2)是指数稳定的。

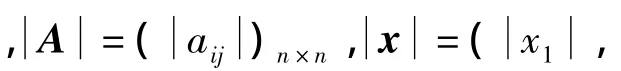
证明:考虑切换 Lyapunov 函数形式为:V(x)=xTPjx，k∈(kτ，kτ+1)，j=i(τ)，

当k=kτ，根据引理 2，得到

由式(5)和式(6)，对于任意k∈(kτ，kτ+1］，得到

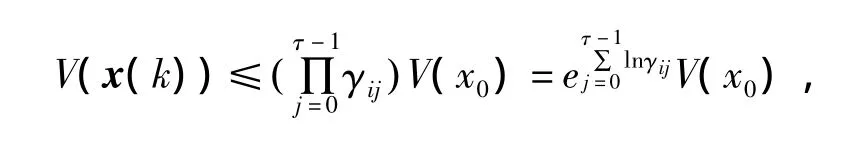
因此，系统(2)是指数稳定的。

3 数值仿真

这一节我们给出数值仿真例子来验证定理的有效性。

例1:考虑线性脉冲离散切换系统(1)，取子系统的个数n=2，切换子系统系数矩阵为

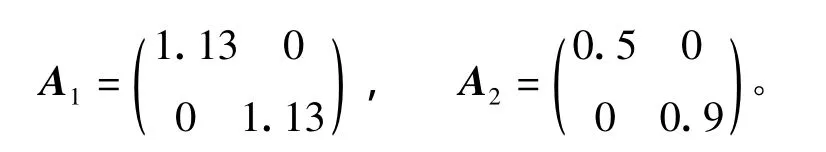
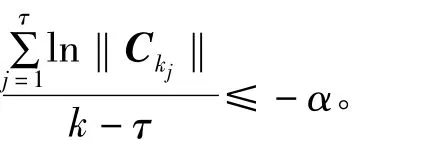
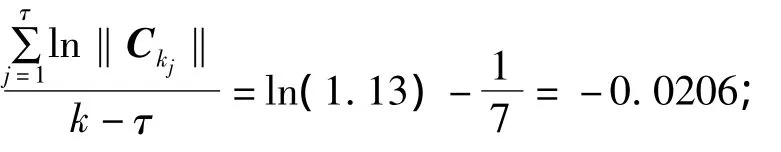
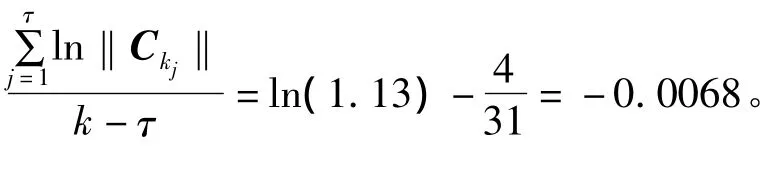
当k∈(k4，k5］时，k-τ＞k4- τ=k4-4=31，ln(max‖Ai(τ)‖)+

由以上运算可知，对于任意k∈(kτ，kτ+1］，∃α ＞0，st.ln(max‖Ai(τ)‖)+

根据定理2.1，可知系统(1)为指数稳定的，如图2所示。

例2:考虑具有非线性不确定扰动项的非线性脉冲离散切换系统(2)，子系统的个数n=2，切换子系统系数矩阵为

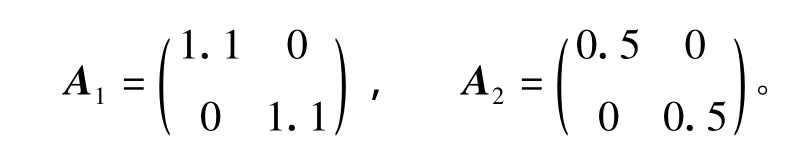
由于λ1(A1)=λ2(A1)=1.1＞1，即∃λ1(A1)=λ2(A1)≥1。故，当系统(2)的系数矩阵切换到A1时，此时的子系统为不稳定的。

由于λ1(A2)=λ2(A2)=0.5＜1，故，当系统(2)的系数矩阵切换到A2时，此时的子系统为稳定的。

取 Pj=I，εj=1，j=i(τ)，kτ=4k，取干扰项

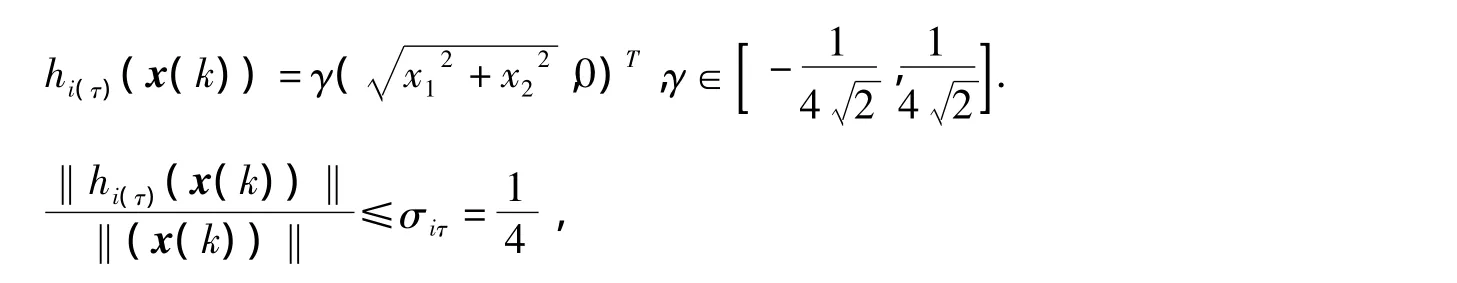
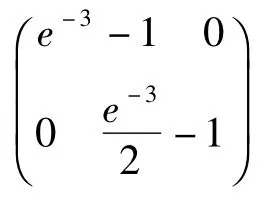
当系统切换到A2时，

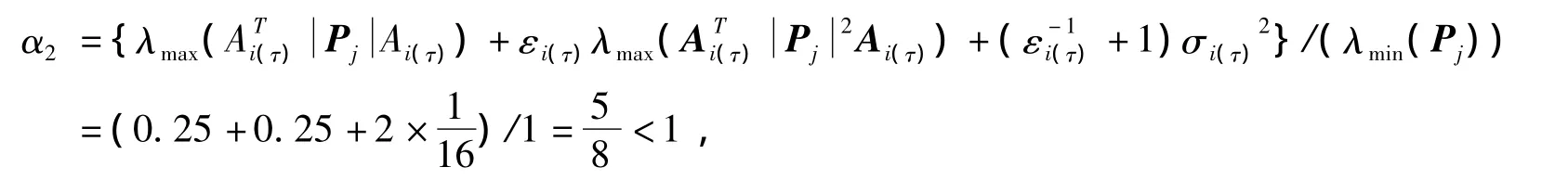
所以 lnα2=-0.47;

当系统切换到A1时，

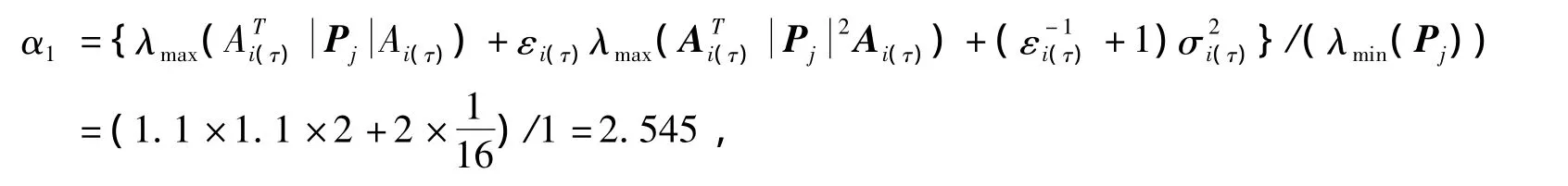
所以 lnα1=0.9341;

当k∈(kτ，kτ+1］，即k∈(4k，4(k+1)］时，令 Sk=lnγj≤(0.9341 ×3-3)k+0.9341 ×3=-0.0659k+2.8023，从而

根据定理2.2，可知系统(2)的状态轨线是指数稳定的，如图3所示。

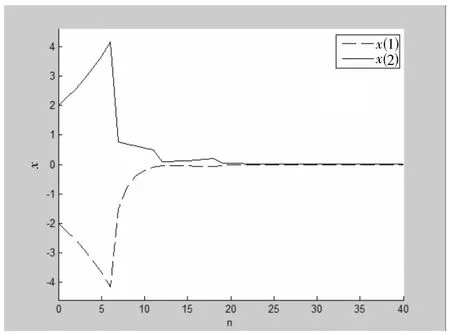
图2 子系统的个数n=2时，系统(1)的状态轨迹序列图

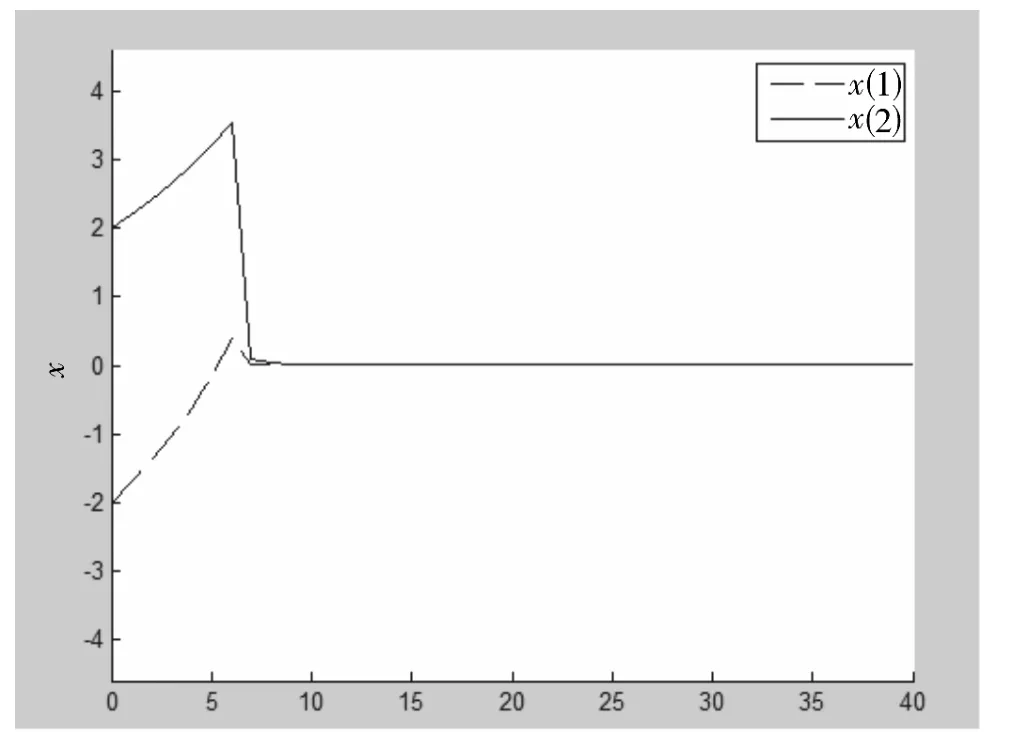
图3 子系统的个数n=2时，系统(2)的状态轨迹序列图

4 结论

脉冲离散切换系统是一类复杂混合系统，具有广泛的实际背景和理论研究意义。这类系统的离散动态与时滞、脉冲行为相互作用，使系统的动态行为变得十分复杂，系统运行机制远未清楚，大量的分析和综合问题等待解决。本文根据指数稳定的定义，研究了线性脉冲离散切换系统的指数稳定性，又利用切换Lyapunov函数方法研究了具有非线性不确定扰动项的脉冲离散切换系统的指数稳定性，从而得到其在任意初始状态及切换序列下指数稳定的充分条件。由于脉冲切换系统的稳定性研究方法尚在发展之中，而且对脉冲切换系统的研究比经典的切换系统更加复杂和困难，因此仍然存在许多有待进一步深入研究和探讨的问题。

［1］Lakshmikantham V，Liu X Z.Impulsive hybrid systems and stability theory［J］.Dynamic System and Application，1998，7:1-9.

［2］Liu B，Liu X Z，Liao X X.Stability and robustness of quasi-Linear impulsive hybrid systems［J］.Journal of Mathematical Analysis and Applications，2003，283:416-430.

［3］刘玉彬，冯伟贞.带时滞二阶时变线性脉冲切换系统的稳定分析［J］.惠州学院学报，2006，26(6):17-21.

［4］董学平，王执铨.一类分布参数脉冲切换系统的稳定性分析及仿真研究［J］.中国科学技术大学学报，2008，38(3):261-265.

［5］Long F，Fei S M.Neural networks stabilization and disturbance attenuation for nonlinear switched impulsive systems［J］.Neurocomputing，2008，71:1 741-1 747.

［6］Zong G D，Xu S Y，Wu Y Q.Robust H-infinity stabilization for uncertain switched impulsive control systems with state delay:An LMI approach［J］.Nonlinear Analysis:Hybrid Systems，2008，2:1 287-1 300.

［7］Xu H L，Kok Lay Teo.Robust stabilization of uncertain impulsive switched systems with delayed control［J］.Computers and Mathematics with Applications，2008，56:63-70.

［8］Li R，Feng Z G，Kok Lay Teo，et al.Optimal piecewise state feedback control for impulsive switched systems［J］.Mathematical and Computer Modeling，2008，48:468-479.

［9］Li Z G，Soh Y C，Wen C G.Switched and impulsive systems:analysis，design and applications［J］.Automatica，2006，42:1 617-1 620.

［10］廖晓昕.稳定性的数学理论及应用［M］.武汉:华中师范大学出版社，1988.

［11］Liu B，Liu X Z.Robust stability of uncertain discrete impulsive systems［J］.IEEE Transactions on Circuits and Systems，2007，54(5):455-459.

［12］Sun Y，Yu G.delay-dependent exponential stability criteria for nonlinear time-varying discrete systems with multiple time delays［J］.Journal of Franklin Institute，1997，334(4):659-666.

［13］Liu B，Liu X Z.Robust stability of uncertain discrete impulsive systems［J］.IEEE Transactions on Circuits and Systems，2007，54(5):455-459.

［14］F Callier，C A Desoer.linear System Theory［M］.Hongkong:Springer-Verlag，1992.

［15］Joäo P Hespanha，Ā Stephen Morse.Switching between stabilizing controllers［J］.Automatica，2002，38:1 905-1 917.

［16］俞立.鲁棒控制—线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002:158-207.