扑翼飞行器平面形状对气动力的影响研究

张小俊, 胡淑玲

(西安交通大学 航天航空学院, 陕西 西安 710049)

扑翼飞行器平面形状对气动力的影响研究

张小俊, 胡淑玲

(西安交通大学 航天航空学院, 陕西 西安 710049)

为了了解扑翼飞行器在扑动过程中的气动力,采用非定常涡格法模拟扑动过程中的气动力计算,得到了刚性扑翼在扑动周期内气动力的变化及尾涡的形态。在此基础上,研究了扑翼的周期平均气动力随扑动频率、幅度、迎角及来流速度的变化关系,并进一步研究了不同的机翼平面形状对气动力的影响。计算结果表明,迎角和扑动频率的增大能够增加扑翼的升力,不同翼面形状的扑翼在升力特性及推力特性方面具有不同的优势。

扑翼飞行器; 非定常涡格法; 机翼平面形状; 平均气动力

force

0 引言

微型扑翼飞行器因具有灵活性、能同时产生升力、推力以及效率方面的优势,不断地吸引着人们的注意,在环境监测、战场侦查及通信中继等领域的应用前景广阔,而实现可控的扑动飞行更是人们自古以来的愿望。对微型扑翼飞行器进行设计的前提是掌握扑翼气动力的变化规律以及确定扑翼本身的平面形状。目前,国内的一些高校已经对扑翼机的气动力开展了一些研究[1-3]。

本文针对扑翼流场的非定常特征,根据非定常涡格法[4]编制了适用于快速求解扑翼飞行器机翼气动力的Fortran程序。应用该程序求得了刚性扑翼在扑动周期内气动力以及扑翼在不同扑动频率、幅度、迎角及流速时的平均气动力。在此基础上,研究了不同的翼面形状对扑翼气动力的影响,研究时保持各个不同形状的翼面具有相同的面积及展弦比,具体采用文献[5]中的部分形状及对其中一个的变化。对不同形状扑翼在不同运动参数下的气动力进行了比较,确定了气动特性较好的几个扑翼形状。本文研究结果对扑翼飞行器的设计及优化具有一定的参考价值。

1 非定常涡格法简介

涡格法采用在翼面上合适位置分布涡环的方法来模拟翼面及尾涡,根据边界条件及离散化的控制方程求解流场的速势方程,进而求得翼面附近流场速度及机翼所受气动力。而非定常涡格法在每个时间步采用上述方法求解一次速势方程,采用机翼尾缘处涡环的脱落模拟尾涡的脱落,能够求解机翼在非定常运动时所受的气动力。非定常涡格法翼面、尾涡环见文献[1]。

除物面及尾涡外,流体视为无粘无旋的,其控制方程为:

2Φ*=0

(1)

式中:Φ*为流场中某处总的势函数,Φ*=Φ+Φ∞;Φ为翼面及尾涡上分布的涡环产生的扰动量。

需满足两种边界条件:

(1)物面边界条件,即无穿透边界条件:

(Φ+v)·n=0

(2)

其中:

v=-vsurface=-[V0+vref+Ω×r]

式(2)表明分布的涡环所诱导的速度与物面相对空气运动速度之和在物面法向的分量为0。

(2)远场边界条件,即无穷远处的扰动为零:

(3)

在机翼后缘还需满足Kutta后缘条件,涡格法的Kutta后缘条件形式为:

-Γup+Γlow+Γwake=0

(4)

式中:Γup和Γlow为上下翼面涡环环量;Γwake为尾缘处尾涡的环量。

此外,机翼后缘在每个时间步将有一尾涡环脱落(见图1),脱落的尾涡与翼面上同一弦向的涡环环量满足Kelvin定律,即某时刻从后缘脱落的尾涡的环量等于翼面上涡环环量随时间的变化:

Γ(t)-Γ(t-Δt)+Γwt=0

(5)

其中:

用涡环模型代表翼面及尾涡将使得流场中的势函数自动满足控制方程及远场边界条件,对物面边界条件离散化,提取出涡环间的影响系数,将使问题变为在每个时间步求解一次线性方程组,这样可求得翼面及尾涡的涡环量分布,进而,根据非定常伯努利方程

可以求得翼面所受法向力,用压力系数可表示为:

(6)

对于刚性翼,vref=-[V0+Ω×r]。将此力沿来流方向及垂直来流向上方向分解即可得机翼所受阻力与升力。

2 扑动飞行算例验证

刚性扑动模型的运动包括前飞及同时伴有的扑动和俯仰运动。前飞速度确定了来流的速度,对于另外两个自由度的运动,本文不考虑俯仰运动,只保留扑动这一自由度的运动,扑动规律也为简单正弦扑动,其俯仰和扑动自由度的运动方程如下:

(7)

算例中:初始迎角α0=5°;初始扑动角β0=0°;扑动角幅度βmax=45°;扑动相位差φβ=0°;扑动角速度ω则随扑动频率f变化。

算例扑翼形状采用文献[2]的形状A,翼面总面积为185.14 cm2,半展长15 cm。与文献中试验运动机构需安装在机身上不同的是:本文不考虑其机身部分,仅计算其翼面部分扑动产生的气动力。在来流速度VT=5 m/s,迎角α=5°,扑动角频率f=8 Hz条件下,扑翼按照如上运动规律在一个扑动周期内产生的尾涡的形态如图1所示。

图1 一个周期内扑翼及尾涡位置示意图Fig.1 Positions of flapping wing and wake vortex in one period of flapping

尾涡能反映扑翼在各个时间的受力情况,目前对扑翼飞行中尾涡的可视化试验并不多。将计算的尾涡结果与文献[4]试验拍得的类似形状扑翼尾涡形态进行比较,两者具有一定的一致性,表明该方法能计算扑翼所受气动力。而扑翼在一个扑动周期内的升力系数和推力系数如图2、图3所示。

图2 一个扑动周期内升力系数的变化Fig.2 Variation of lift coefficient in one period of flapping

图3 一个扑动周期内推力系数的变化Fig.3 Variation of thrust coefficient in one period of flapping

由图2和图3可见,升力在扑动周期内有一正峰值与负峰值,其周期平均值与迎角有关;推力在扑动周期内则有两个峰值。

3 不同平面形状扑翼气动特性

3.1 扑翼的平面形状

扑翼平面采用文献[2]中的A,B,C,D,E,F翼面形状,以及将形状A沿弦向反转后得到的一个形状,面积和展长分别为185.14 cm2和15 cm,排序后如图4所示。其中,形状A前缘平直、后缘接近椭圆曲线的形状常被用作扑翼机翼面形状。为了加强翼面刚度同时保持翼面柔性,常常会在翼面合适角度布置一根加强杆;形状D则类似昆虫翅膀的形状,具有较为圆润的前后缘。几个形状的差别体现在:前后缘的形状不同;翼面前后、内外侧面积分布不同。

图4 六种平面形状示意图Fig.4 Six shapes of wing plane

3.2 扑翼气动力随扑动频率的变化

保持来流速度VT=5 m/s、扑动角幅度βmax=45°及迎角α=5°,在扑动频率变化时,上述形状的扑翼升力系数和推力系数如图5、图6所示。

图5 扑翼升力系数随频率的变化曲线Fig.5 Curve of lift coefficient with frequency

图6 扑翼推力系数随频率的变化曲线Fig.6 Curve of the thrust coefficient with frequency

由图5可见,在其他条件相同时,扑翼平均升力系数在一定频率范围内随扑动频率的增加而增加。不同形状扑翼升力特性排列顺序为:E>C>A>D>B>F,其中前三者(E,C,A)的升力特性差别并不大,而形状F的升力特性最差。

由图6可见,在其他条件相同时,扑翼平均推力系数在一定频率范围内也随扑动频率的增加而增加。不同形状扑翼推力特性大致为:F>D≥A>B>C>E,而形状F的推力特性明显高于其他形状扑翼,形状E的推力特性最差。

3.3 扑翼气动力随扑动角幅度的变化

保持来流速度VT=5 m/s、扑动频率f=8 Hz及迎角α=5°,在扑动角幅度βmax变化时,上述形状的扑翼升力系数和推力系数如图7、图8所示。

图7 扑翼升力系数随扑动角幅度的变化曲线Fig.7 Curve of the lift characteristics with βmax

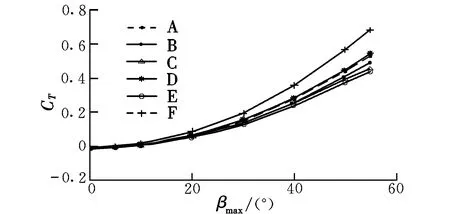
图8 扑翼推力系数随扑动角幅度的变化曲线Fig.8 Curve of the thrust characteristics with βmax

由图7可见,对于多数扑翼形状(A,B,C,E),扑动角的增加对升力影响不大;对于D,F形状的扑翼,扑动角的增加会导致升力的一定下降;不同形状的扑翼在不同的βmax下的升力特性表现并不相同。总的来看,形状A,C,E的扑翼升力特性较好。

由图8可见,扑动角幅度的增加将导致扑翼推力的增加。扑翼推力特性排序为:F>D≥A> B>C>E,推力特性表现与频率变化时相同。

3.4 扑翼气动力随迎角的变化

保持来流速度VT=5 m/s、扑动频率f=8 Hz及扑动角幅度βmax=45°,在迎角α从0°至18°变化时,上述形状的平扑翼升力系数和推力系数如图9、图10所示。

图9 扑翼升力系数随迎角的变化曲线Fig.9 Curve of the lift characteristics with AOA

图10 扑翼推力系数随迎角的变化曲线Fig.10 Curve of the thrust characteristics with AOA

由图9可见,迎角的增大将显著提高扑翼的升力特性。与频率及扑动角幅度变化相比,在飞行速度相同的情况下,迎角是影响扑翼升力的主要因素。不同形状的扑翼升力特性排序为:E>C>A> D>B>F,其中前三者(E,C,A)差距并不大,形状F的升力特性仍然是最差的。

由图10可见,迎角的增大将导致扑翼推力一定程度的降低。不同形状扑翼的推力特性排序为:F>D>A>B>C>E,其中形状F的推力特性仍明显高于其他形状扑翼,而形状E的推力特性仍是最差的。

3.5 扑翼气动力随流速的变化

保持迎角α=5°、扑动频率f=8 Hz及扑动角幅度βmax=45°,在来流速度VT从5 m/s至10 m/s变化时,扑翼升力系数和推力系数如图11、图12所示。

图11 扑翼升力系数随流速的变化曲线Fig.11 Curve of the lift characteristics with velocity

图12 扑翼推力系数随流速的变化曲线Fig.12 Curve of the thrust characteristics with velocity

由图11可见,其他条件相同时,流速的增大将导致扑翼的升力系数一定程度的降低,不过升力系数随流速增大将逐渐趋于一个稳定的值,可见扑翼的实际升力将随流速的增大而增大。扑翼升力特性排序为:E>A>C>D>F>B,其中前三者(E,A,C)差距并不大,此时形状B的升力特性最差。

由图12可见,其他条件相同时,流速的增大将导致扑翼推力系数的降低。扑翼推力特性排序为:F>D>A>B>C>E。

3.6 综合比较

综上所述,不同扑翼形状的特性为:形状E的升力特性最好但推力特性最差;形状F与之相反;形状A的升力特性及推力特性都排在第三,综合性能较好;形状B的升力特性及推力特性都排在后三位内,综合性能不佳;而形状C和D分别在升力特性及推力特性方面有一定优势,其中形状D的两种特性基本上都排在前四个以内,故综合性能好于C。综合性能较好的形状排序为:A>D>C,所以形状A这种前缘平直而后缘近似椭圆的类似鸟翼的平面形状成为众多扑翼机选用的形状,形状D这种类似昆虫翅膀的形状在气动特性方面也具有一定优势。

4 结论

(1)在扑动频率、扑动角幅度、迎角及流速这几个扑翼的运动参数中,对扑翼升力系数增加起决定作用的是迎角,而扑动频率的增大也能在一定程度上增大扑翼的升力系数。

(2)扑动频率及扑动角幅度的增加都能增大扑翼的推力,而增大迎角将使扑翼推力有一定程度的减小。

(3)来流速度的增加将使得扑翼的升力系数及推力系数同时下降,并使升力系数渐趋于一个稳定值,扑翼实际的升力将随来流速度的增加而增加。

(4)机翼的平面形状对于扑翼气动特性的影响是可观的。不同翼面形状的扑翼在升力特性及推力特性方面具有不同的优势。从翼根到翼尖以及从前缘到后缘过于剧烈的形状变化不利于产生好的综合气动特性,类似鸟翼及昆虫翅膀的形状(A和D)则具有较好的综合气动特性。

[1] 余春锦.柔性扑翼微型飞行器的气动特性研究[D].南京:南京航空航天大学,2008.

[2] 肖天航,段文博,昂海松.仿鸟柔性扑翼气动特性与能耗的数值研究[J].空气动力学学报,2011,29(6):709-718.

[3] 杨淑利,宋文萍,宋笔锋,等.微型扑翼飞行器机翼气动特性研究[J].西北工业大学学报,2006,24(6):768-773.

[4] 曾锐.仿鸟微型扑翼飞行器的气动特性研究[D].南京:南京航空航天大学,2004.

[5] Malolan V,Dineshkumar M,Dr Baskar V.Design and development of flapping wing micro air vehicle [R].AIAA-2004-40,2004.

(编辑：李怡)

Influence of wing shape on the aerodynamic characteristics of flapping-wing vehicle

ZHANG Xiao-jun, HU Shu-ling

(School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China)

To know the aerodynamic force of flapping-wing vehicle during the flight, aerodynamic force calculation was simulated by using the unsteady vortex lattice method. The aerodynamic force’s change and the wake’s shape of some flapping wings were obtained. Then, the change of the average aerodynamic force with some parameters was analyzed, such as flapping frequency, flapping angle range, AOA and the inflow speed. Furthermore, the influence of different shapes of flapping wings on the aerodynamic force was analyzed. The results show that the increase of the AOA and flapping frequency could contribute to the increase of average lift. The shape of wing has an influence on the lift and thrust.

flapping-wing vehicle; unsteady vortex-lattice method; wing shape; average aerodynamic

2014-05-29;

2014-09-22;

时间:2014-11-04 08:28

张小俊(1990-)，男，江苏扬州人，硕士研究生，研究方向为扑翼飞行器气动特性; 胡淑玲(1971-)，女，陕西西安人，副教授，博士生导师，研究方向为计算流体力学。

V211.3

A

1002-0853(2015)01-0017-04