基于蒙特卡洛仿真的高空尾涡运动特性

2021-12-22魏志强李晓晨

空军工程大学学报 2021年5期

魏志强，李晓晨

(中国民航大学空中交通管理学院，天津，300300)

飞机机翼在产生升力的过程中，上翼面及下翼面之间的压强差将会导致在左右翼尖处形成转向相反的翼尖涡流场[1]。当后方飞机不慎进入前机的尾涡流场时，可能会发生失速、滚转、急剧俯仰等危险情况，严重威胁飞行安全[2]。近年来，空域繁忙程度的增加以及空域资源的日趋紧张使得充分利用高空资源越来越迫切，其中尾涡遭遇问题是高空飞行高度层垂直间隔缩减的重要限制因素。

空中交通流量的持续增长对空域利用效率提出更高要求。我国在8 900～12 500 m的平飞巡航高度区间内实施缩小最低垂直间隔(reduced vertical separation minimum, RVSM)，将飞行高度层之间的垂直间隔标准由600 m缩小到300 m，增加了空域容量。近年来，国际民航组织(international civil aviation organization，ICAO)开始着手研究在RVSM空域上扩高度层中实施缩小垂直间隔的可行性[3]，但尚未考虑飞机尾流的消散和运动对下方飞机飞行安全的影响问题。

目前针对尾涡流场参数的仿真计算在技术上可分为基于流体动力学方法的数值模拟技术和基于涡流演变机理的快速仿真计算技术。飞机尾涡流场的数值模拟主要包括大涡模拟、雷诺平均及分离涡模拟方法[4-6]。受计算机计算方法及运算能力的限制，在对飞机尾涡进行数值模拟时，有限的网格数量使得对尾涡形成阶段的模拟较为清晰，但对于尾涡的消散和运动阶段的数值模拟效果尚不够理想。在尾涡流场参数的仿真计算方面，国外研究者通过建立数学模型描述尾涡消散机制。Holzäpfel等建立两阶段尾涡消散模型(two-phase wake vortex decay，D2P)来计算尾涡强度的衰减情况[7]。Sarpkaya等基于数值模拟数据的分析，认为尾涡的消散速率与雷诺数关系不大，而主要取决于大气湍流度[8-9]。Proctor等建立了尾涡流场快速预测模型，并应用于终端区尾流仿真系统平台。这些数学模型由于响应快速、运算高效、相对简化而被广泛应用于尾涡流场参数的仿真计算中[10-11]。

国内研究者主要致力于尾涡流场建模及尾涡参数计算方面的研究。魏志强等利用“天河一号”超级计算机进行数值模拟实验，计算分析了不同侧风下的涡量衰减、涡心速度等参数的变化情况[12]。沈淳等基于雷达探测反演方法预测飞机尾流行为及尾涡危险区域，为尾流动态安全间隔标准制定提供支撑[13]。谷润平等建立多目标优化模型，以诱导滚转力矩系数反映尾涡遭遇严重度，应用于飞机编队飞行的前后机相对位置优化[14]。魏志强等分析了飞机加装翼尖小翼后尾流安全间隔的变化情况，以及航空器重新分类时的尾流遭遇风险问题[15-16]。国内外研究者在尾涡流场参数仿真计算和安全间隔标准的制定方面开展的研究主要针对中低空及飞机的起降阶段，未对12 500 m以上高空空域的尾涡流场特性进行分析。

为解决上述问题，文中首先建立了飞机尾涡物理模型。然后以某重型飞机为例分析12 500 m飞行高度以上的高空尾涡流场运动特性，根据蒙特卡洛方法仿真计算高空与中低空的尾涡下沉高度差异；最后分析高空尾涡涡核下沉运动的影响因素。研究结果为在RVSM空域上扩高度层中实施缩小垂直间隔标准提供参考，以期提高空域利用效率，降低高空尾涡遭遇风险。

1 飞机尾涡物理模型

1.1 尾涡初始强度计算模型

飞机尾涡一般使用涡旋环量Γ表示其强度。根据圆柱绕流气动力知识，机翼微元上的升力计算公式为：

l(x)=ρ∞v∞Γ(x)

(1)

式中：ρ∞为大气密度；v∞为飞机真空速；Γ(x)为翼剖面附着涡环量；x为翼剖面与飞机纵轴之间的距离。对整个翼展积分，飞机升力L的计算公式为：

(2)

式中：B为飞机翼展。对于后掠翼飞机，翼剖面环量的计算公式为：

(3)

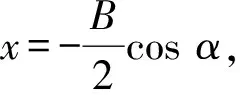
(4)

所以，得尾涡初始强度计算公式如下：

(5)

式中：n为飞机法向过载；W为飞机质量。由上式可以看出，尾涡初始环量的大小与飞机质量、空气密度、飞机速度、翼展等因素相关。

1.2 尾涡消散过程

综合考虑尾涡消散的随机特性，Holzäpfel和Robins应用激光雷达开展多次尾涡探测试验[17]，在D2P模型基础上添加随机扰动项，形成尾涡随机两阶段消散模型(probabilistic two-phase wake vortex decay，P2P)。尾涡的消散主要受大气参数及飞机特性影响，P2P模型可以用来描述不同飞行高度处的尾涡消散情况。

为了计算方便，通常使用无量纲基准参数。常用的无量纲基准参数包括参考下沉速度w0和尾涡参考时间t0，具体计算公式如下：

(6)

(7)

式中：b0为尾涡初始涡核间距，通常为πB/4。

根据P2P模型，尾涡的消散可分为2个阶段：扩散阶段及快速衰减阶段。在扩散阶段，尾涡消散的速率较为缓慢，尾涡环量计算公式如下：

(8)

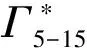
(9)

ε*=(εb0)1/3/w0

(10)

用浮力频率N表征大气层结稳定度，无因次浮力频率N*的计算公式如下：

(11)

(12)

式中：hf为飞机的飞行高度；T为所在飞行高度的温度；Cp为定压比热。与平流层相比，通常对流层内大气层结稳定度较低。

1.3 尾涡下沉模型

尾涡形成后由于相互诱导作用而向下运动，涡核位置发生变化。涡核下沉速度vs及经时间t涡核下沉高度hs的计算公式如下：

(13)

(14)

在实际大气中，尾涡的强度消散和涡核下沉运动会对下方飞机的飞行安全造成不利影响。通过计算并对比高空和中低空的尾涡运动差异，可以定量地评估在高空实施缩减尾流垂直间隔的可行性及安全性。

2 尾涡运动特性计算分析

2.1 计算模型的验证分析

SESAR和EUROCONTROL针对欧洲空域内飞机巡航阶段的尾涡遭遇安全问题联合开展R-WAKE项目[18]。分别以形成尾涡流场的前机为A320、A330、B777，飞行高度为39 500 ft，在涡流耗散率ε及浮力频率N均为0的条件下，参考文献[18]给出R-WAKE项目的尾涡遭遇模拟数据。统计前机后方不同纵向位置处的尾涡涡核下沉高度，与第1节中模型的计算结果进行对比，如表1所示。相对误差基本在4.2%范围内，说明文中模型的计算精度可以接受。

表1 尾涡涡核下沉高度数据对比

2.2 仿真实验条件

考虑在飞机飞行过程中飞机的重量、速度及大气参数的不确定性，采用蒙特卡洛方法(Monte-Carlo approach)对尾涡的运动情况进行仿真模拟。蒙特卡洛模拟属于概率分析法，使用随机变量代替常量，同时保证随机变量符合一定的概率分布，使最终结果更加逼近使用常量时所得到的计算结果。蒙特卡洛仿真的具体实验条件如表2所示。

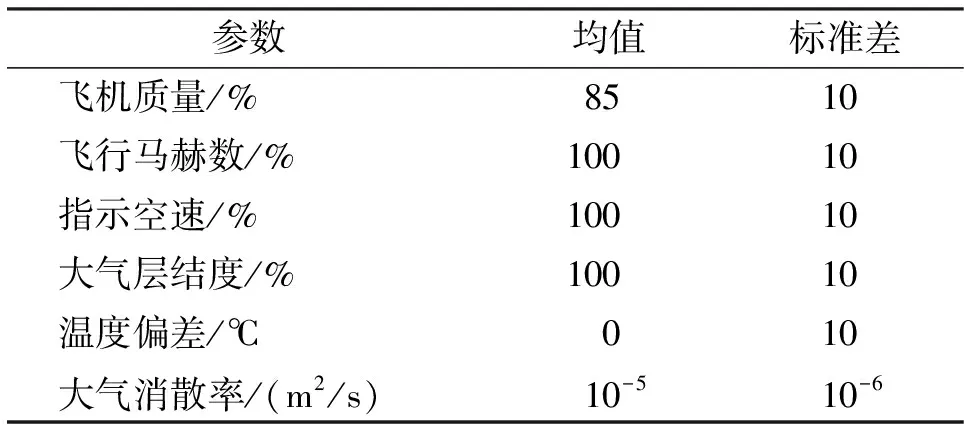
表2 蒙特卡洛仿真实验条件

2.3 尾涡涡核下沉计算分析

根据式(1)～(5)，使用蒙特卡洛方法对某重型机在不同飞行高度处的尾涡初始环量进行10 000次仿真计算，得到不同飞行高度处的尾涡初始环量均值如图1所示。由图1可以看出，高空中的尾涡初始环量较大，15 000 m飞行高度处的尾涡初始环量约为中低空尾涡初始环量最小值的3.1倍。因此在高空飞行范围内，仍有尾涡遭遇不安全事件的发生和报道。

图1 蒙特卡洛仿真模拟的尾涡初始环量Γ0均值

前机下方形成的尾涡危险区与后机所能承受的尾涡强度Γa有关，尾涡危险区在垂直范围上表示为尾涡环量消散到Γa时的涡核下沉高度。为反映不同飞机所能承受的尾涡强度不同，令Γa分别为150 m2/s、100 m2/s、50 m2/s，计算尾涡涡核下沉高度。依据机型性能数据和仿真实验条件，使用蒙特卡洛方法对某重型机在不同飞行高度处的尾涡涡核下沉高度进行10 000次仿真计算，得到尾涡下沉高度平均值和标准差，仿真结果如图2和图3所示。

从图2可以看出，12 500 m以上的高空中，尾涡环量消散到Γa时涡核下沉高度随飞行高度的增加而增加。这是因为飞行高度增加后，尾涡初始环量增大，因此由涡核的下沉高度计算公式可知，飞行高度增加，高空涡核的下沉速度相对较大，导致高空涡核下沉高度增加。从图3可以看出，12 500 m以上的高空中，随飞行高度增加，涡核下沉高度的标准差降低，因此外界因素的不确定性变化对高空涡核下沉运动的干扰较小。

图2 蒙特卡洛仿真模拟的涡核下沉高度均值

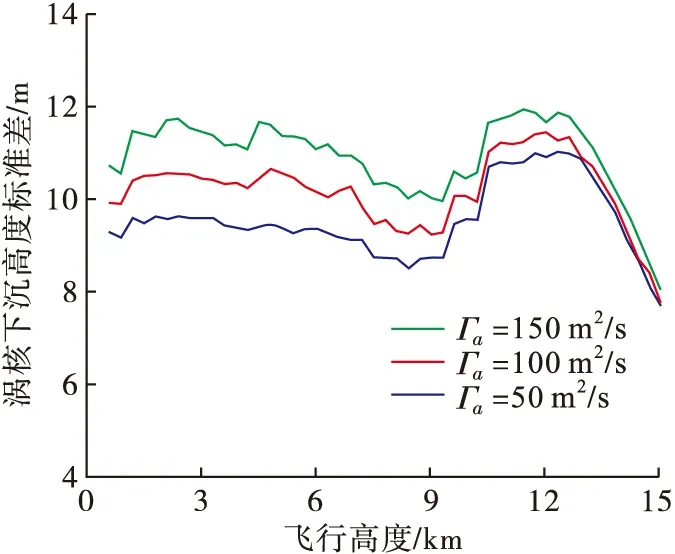
图3 蒙特卡洛仿真模拟的涡核下沉高度标准差

与中低空相比，12 500 m以上高空中的涡核下沉高度在增大。为了计算12 500 m以上高空尾涡涡核下沉高度增大的幅度，设尾涡环量消散到Γa时，高空尾涡涡核最大下沉高度为hmax，中低空尾涡涡核最小下沉高度为hmin，则尾涡涡核下沉高度差值Δh的计算公式如下：

Δh=hmax-hmin

(15)

2.4 高空与中低空的涡核下沉运动差异性分析

计算不同蒙特卡洛仿真实验次数下的Δh，统计平均值与相对标准差，结果如图4及图5所示。可以看出，高空尾涡涡核下沉高度平均增加量为42.4～49.7 m，相对标准差为14.4%～17.6%。当实验次数超过10 000次后，计算结果与仿真实验次数基本无关联。

图4 不同实验次数下的Δh平均值

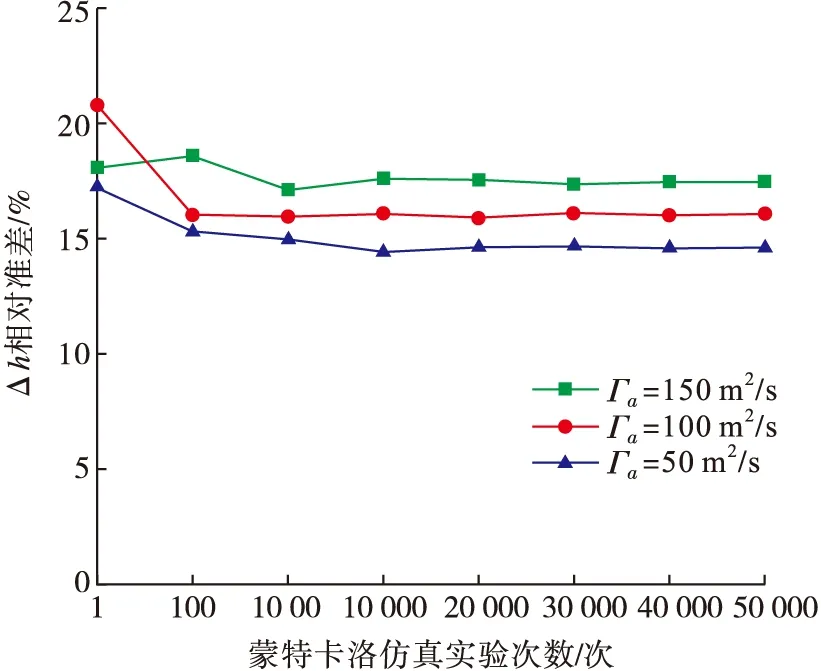
图5 不同实验次数下的Δh相对标准差

当环量消散到100 m2/s，统计50 000次蒙特卡洛仿真实验下的Δh分布情况，绘制频数分布直方图及对应的概率密度函数曲线，如图6所示。由图6可以看出，Δh的仿真值大部分分布在35～55 m范围内，呈正态分布规律。

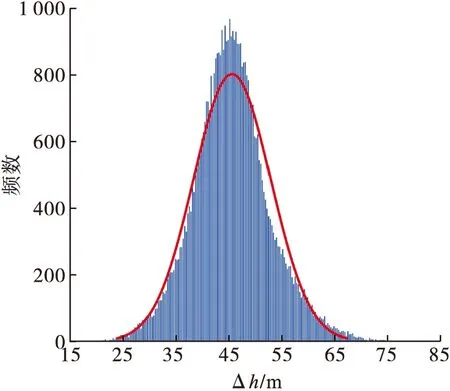
图6 Δh的分布概率密度函数

表3为Δh的具体区间分布情况。由表3可以看出，Δh最大值所在区间为80～85 m，最小值所在区间为15～20 m。涡核下沉高度差值在45～50 m区间内出现次数最多，占比约为28.3%。根据蒙特卡洛仿真模拟得到的计算数据，当飞机参数及外界因素发生不确定性变化时，高空与中低空尾涡涡核下沉高度存在较大差异。

表3 Δh的区间分布

3 影响因素分析

飞机特性及大气条件均会对尾涡的消散及运动造成影响。此节分析飞机质量以及大气湍流度的变化对RVSM空域上扩高度层中的尾涡涡核下沉高度的影响。

3.1 飞机质量对尾涡下沉高度的影响

飞机的形状和质量影响形成尾涡的初始强度，进而影响尾涡的消散和涡核的运动，其中飞机质量是主要的影响因素[19]。为了分析飞机质量对尾涡下沉高度的影响，按照飞机质量350～390 t，其余初始条件同2.2节的条件，由尾涡物理模型计算15 000 m飞行高度处当尾涡环量消散到100 m2/s时对应的尾涡下沉高度。图7为不同飞机质量下进行10 000次蒙特卡洛仿真实验数据的统计值，包括中位数、60%～90%概率值等。

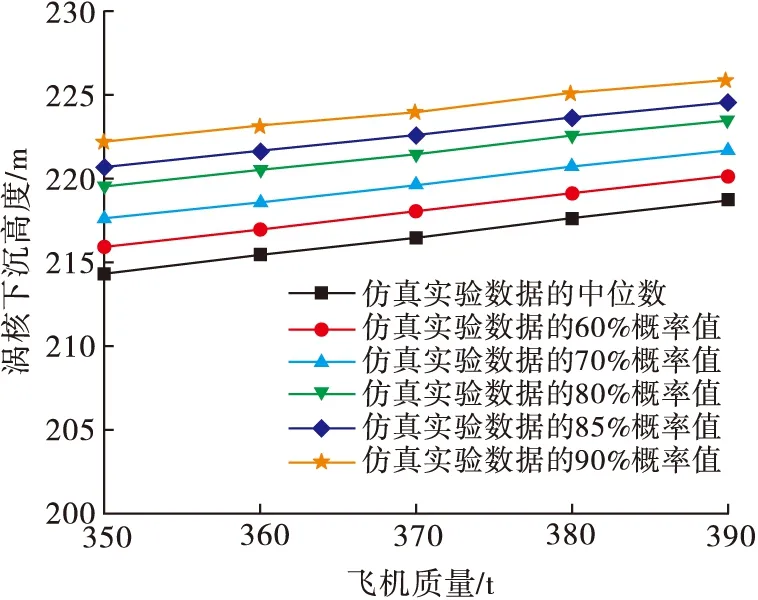
图7 不同飞机质量下尾涡下沉高度变化趋势

从图7可以看出，高空尾涡涡核下沉高度随飞机质量的增加而增加。这是因为飞机质量增加后，导致尾涡初始环量增加，涡核的下沉速度相对较大，因此由涡核下沉高度的计算公式可知，飞机质量增加，导致涡核下沉高度增加。飞机质量从350 t增加到390 t的过程中，涡核下沉高度最大增加4.4 m，变化范围为1.7%～2.1%。

3.2 大气湍流度对尾涡下沉高度的影响

高空中的大气湍流度较低，为了分析大气湍流水平对尾涡涡核下沉高度的影响，按照涡流耗散率10-5～10-3m2/s3，其余初始条件同2.2节的条件计算15 000 m飞行高度处当尾涡环量消散到100 m2/s时对应的尾涡下沉高度。图8为不同大气湍流度下进行10 000次蒙特卡洛仿真实验数据的统计值，包括中位数、60%～90%概率值等。