结构模型制作中的相贯线展开应用

何大治， 赵艳霞， 闫磊源

(华北水利水电大学土木与交通学院，河南 郑州 450011)

结构模型制作中的相贯线展开应用

何大治， 赵艳霞， 闫磊源

(华北水利水电大学土木与交通学院，河南 郑州 450011)

按相贯线裁剪制作结构模型，可大量节省构件连接时的材料用量，是结构模型质量优化的一个重要途径。讨论了在模型制作过程中常见的两杆相贯和三杆相贯的情况，利用圆柱坐标矩阵旋转变换的方法，构建了相贯线及其展开曲线的方程，分析了使用相贯线进行杆件剪裁的方法，将该方法应用于结构模型制作过程，可使模型在质量上得到了很大优化。

结构模型；节点；相贯线；展开曲线；坐标变换

结构模型制作是检验土木工程专业大学生专业知识应用能力的一种有效手段，近年来，已发展成为全国九大大学生学科竞赛之一，各省的大学生结构模型竞赛也相继出现，极大地提高了土木工程专业大学生的实践动手能力和知识理解深度。

在设计模型时，多选择圆管形杆件，这类杆件的制作较为方便，且受力性能良好，但是在节点连接处较难处理，许多模型在制作时，为保证节点的安全，对连接做了过多的粘结处理，从而出现节点处过分臃肿，杆件受力路径不明确，结构自重增大等缺陷，这些问题的出现表明学生们在节点的细节处理上精确度不足，且解决问题的手段较少。笔者曾带领学生参加过两届河南省结构模型竞赛，在参赛中发现上述问题是较多参赛队伍的通病，即使在全国大赛中也存在相同的问题[1-2]。实际上，在处理模型节点时，只要合理运用画法几何中关于圆柱相贯线展开的知识就可以使问题得到解决，在不降低承载能力的前提下减少模型的自重。本文通过对模型制作过程中常遇到的T形和K形节点进行相贯线分析，构建相贯线展开曲线的一般数学方程，为今后参加同类竞赛提供一些思路。

1 相贯线展开的数学方法

常用的立体相贯线的求解方法有两种，图解法[3-4]和解析法[5-7]，在设计和制作模型时，需对模型进行多次优化，使用图解法绘制相贯线效率较差。如使用解析法，可根据相贯线的解析方程编制计算程序，进行模型优化时，直接调整初始参数，即可得到相贯线的数值曲线，能极大地提高设计的效率。

1.1 T形节点

模型结构不同，在节点处相交的杆件数量也不相同。在一个节点上通常是两杆或三杆相交，以“T”或“K”形节点居多，如果是“T”形节点，可将节点构建成如图1所示的两半径为r1和r2圆柱体相交形式，以r1圆柱的旋转轴为z轴建立直角坐标系O1x1y1z1，以r2圆柱的旋转轴为z轴建立直角坐标系 O2x2y2z2，圆柱 r1与圆柱 r2之间的夹角为两坐标系 z轴之间的夹角α。此外，由于模型杆件多为轴线相交形式，坐标原点偏移值为零，两个圆柱的坐标系原点为同一点。

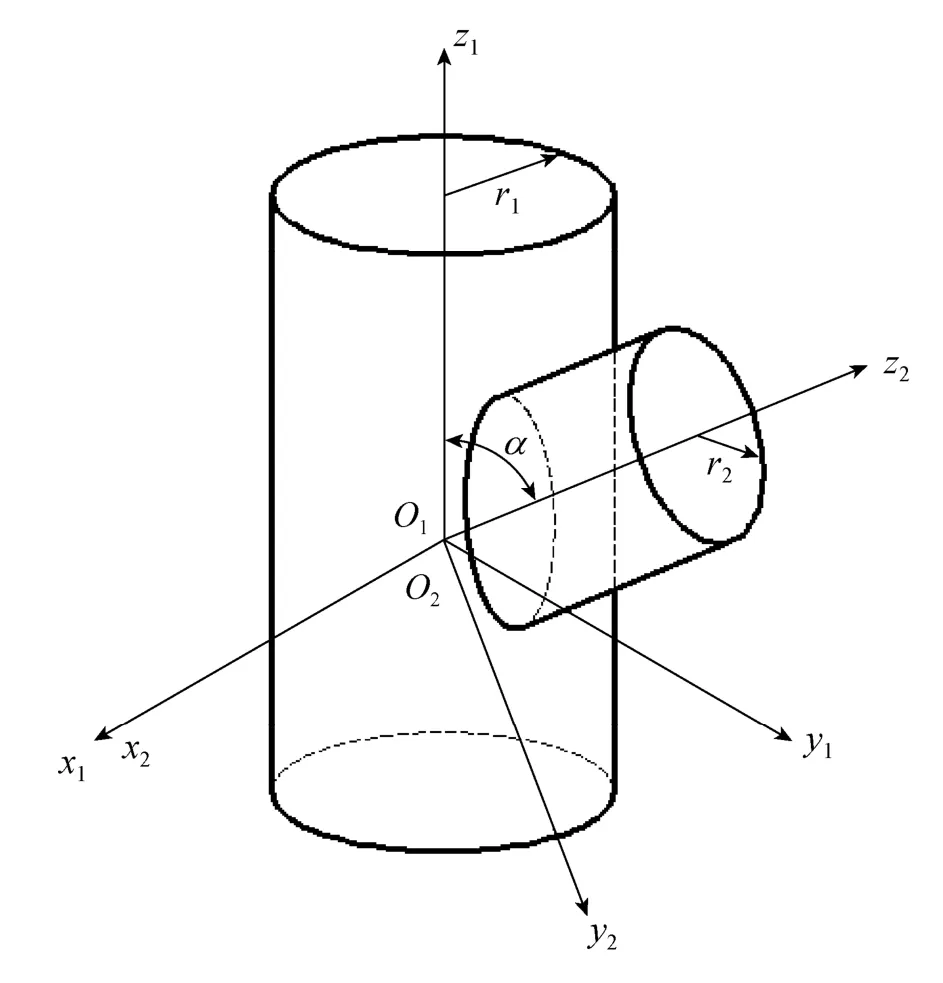
图1 T形节点

圆柱体r1与圆柱体r2的柱面坐标可以表示：

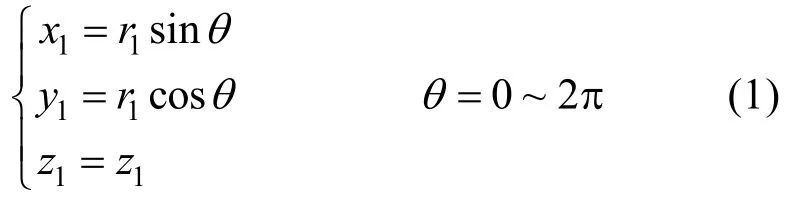
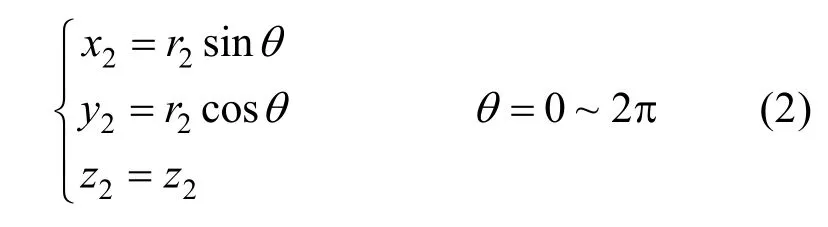
求解两圆柱体的交线，必须将两组方程通过旋转变换统一到相同坐标系下，圆柱体r2的表达式变换到直角坐标系O1x1y1z1下，其变换矩阵为：

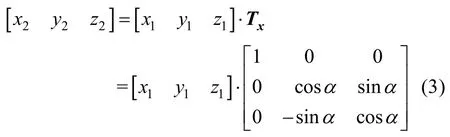
写成方程组的形式为：

上式即为圆柱体 r2的坐标在直角坐标系 O1x1y1z1下的表达式，将式(1)代入式(4)中，可得两圆柱体相贯线在O1x1y1z1坐标系下的表达式：

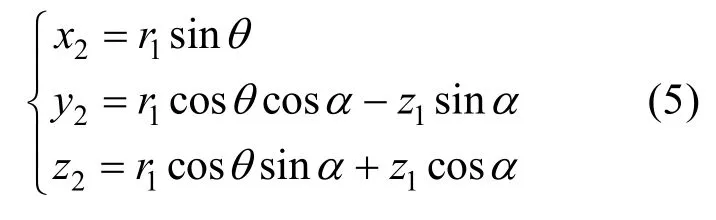
圆柱体r2的直角坐标形式可表达为：

将式(5)代入式(6)中，可得相贯线的z1坐标表示：

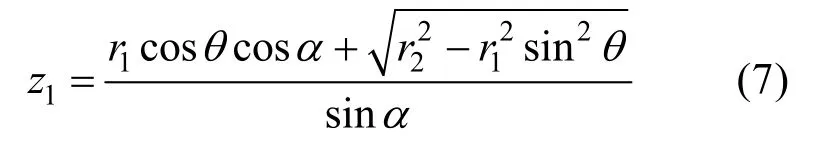
式中，α、r1和r2为常数，θ为从0到2π的变量，取θ=0，0.1π，··，2π，根据式(7)即可绘制出两圆柱体的相贯线。

式(7)为 O1x1y1z1坐标系下的相贯线表达式，根据计算得到的数值可在杆件 r1上绘制相应曲线，若是在O2x2y2z2坐标系下表达相贯线，则旋转角度为-α，并按式(4)～(7)方式计算z2的值。式(8)为O2x2y2z2坐标系下相贯线的解析表达式。

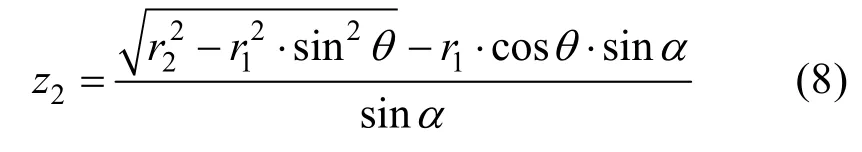
需要注意的是，如果两根杆件的半径是相同的，式(8)中θ取值区间可为[0，2π]，若两杆件半径不同，按图2所示不同直径杆件相贯俯视图，由图中投影关系可知，在直径较小杆件坐标系O2x2y2z2下，相贯线的 θ取值区间仍为[0，2π]，而在较大直径的杆件坐标系O1x1y1z1下表示时，θ取值区间取为[-φ，φ]，φ的取值可根据式(9)确定。

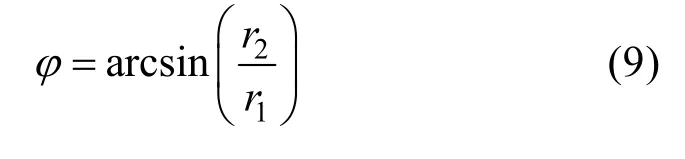
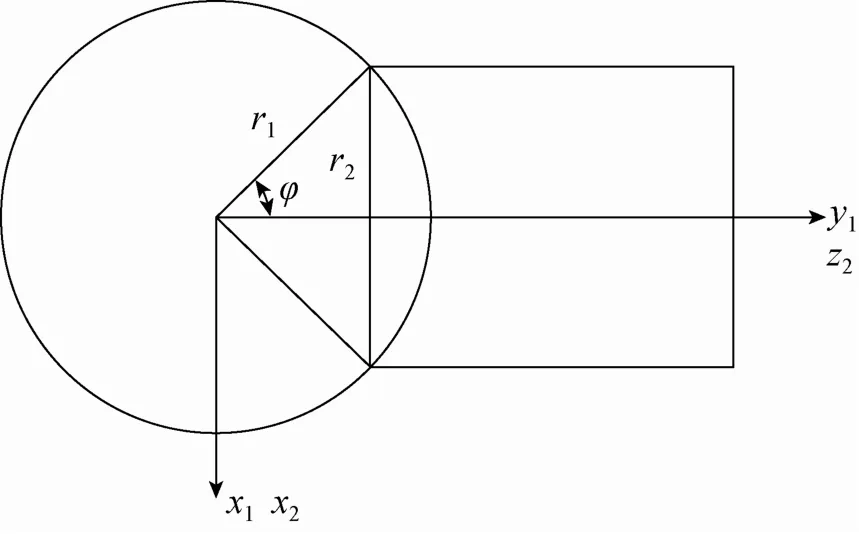
图2 θ取值区间

图3所示为半径均等于10 mm的杆件相交时的相贯曲线展开图，两杆件之间的夹角α等于60°。

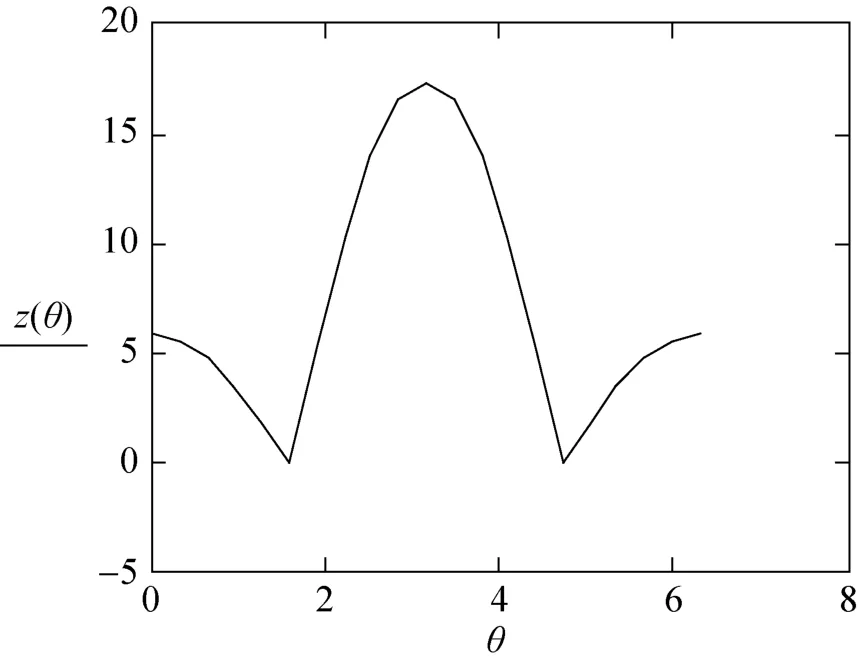
图3 T形节点相贯线展开

1.2 K形节点

K形节点有三根杆件相交，其中一根为贯通直杆，另外两根除与贯通直杆相交外，两根杆件之间也存在相交关系。在结构模型中为避免构件偏心，及在节点处产生弯矩作用，通常都将节点设计为所有杆件的相交点，因此，在本文中，也针对此情况进行讨论。

K形节点相贯线的计算方法与T形节点类似，求解贯通直杆与另外两根杆件之间的相贯线方程，得到两组方程，并再次求交，得到相贯曲线之间的交点。

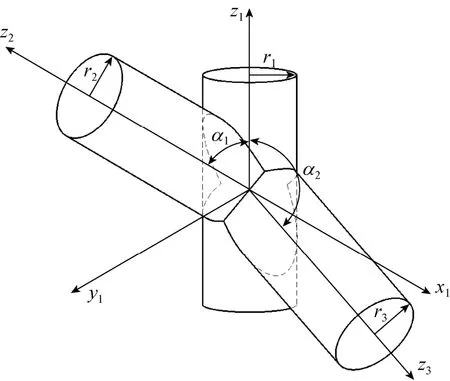
图4 K形节点

如图4所示，在节点处三杆相交，半径为r2的杆件2可看作是半径为r1杆件1绕其x1轴旋转

1α所得，半径为r3的杆件3可看作是杆件1绕其y1轴旋转2α所得，根据T型节点的计算方法，分别对杆件1与杆件2、杆件1与杆件3，以及杆件2与杆件 3求解相贯线方程，其中，求解杆件 1与杆件2和杆件3之间的相贯线可参考T型节点做法，杆件2与杆件3之间的相贯线则需要将其中一个杆件旋转两次，具体做法如下：

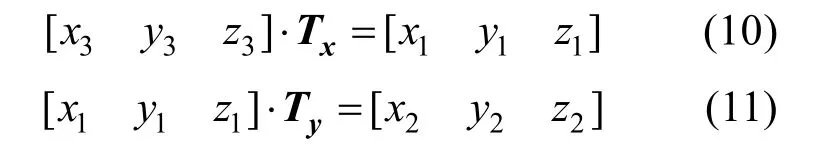
将式(10)带入式(11)可得：

式(12)展开后可得：

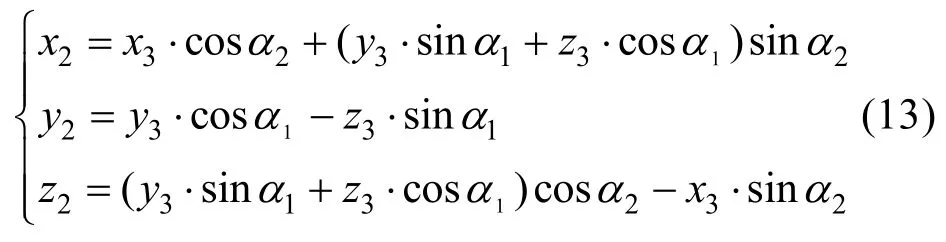
将式(13)中x3、y3用圆柱坐标表示则为：

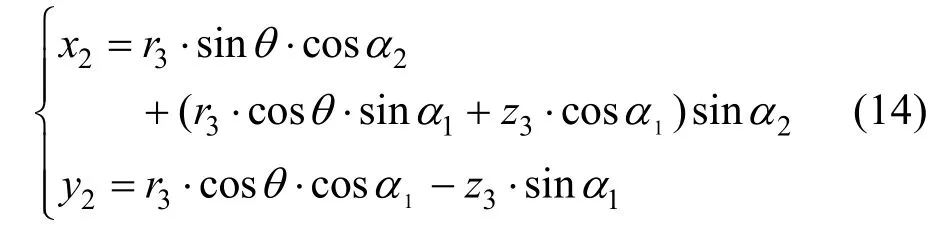
将式(14)代入式(6)，可得杆件2与杆件3之间相贯线 z3坐标的解，z3坐标的求解过程可借助数学软件计算得到，如式(15)所示。

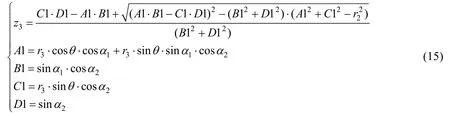
如果两根杆件的半径是相同的，式(15)中θ取值区间可为[0，2π]，若两杆件半径不同，r3〉 r2，则θ取值范围为[-φ，φ]，φ的取值可根据式(16)确定。

同理，式(15)表示的相贯线也可在坐标系O3x3y3z3下表示，解析过程不再详述。

图5所示为杆件半径均等于10 mm，杆件之间夹角1α=30°，2α=45°时的相贯线曲线图形。

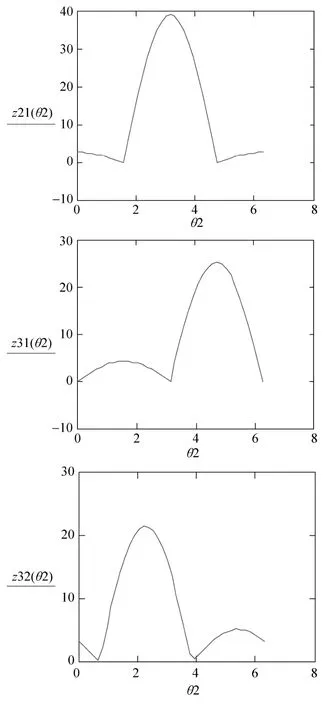
图5 K形节点相贯线展开图

2 K形节点相贯线的其他情况

相比较T形节点而言，K形节点的相贯线的计算较为复杂，这是因为要考虑杆件相交的不同情况，在前述内容中，在K形节点处，三根杆件两两相交，组成了三个平面，其中两个平面是相互垂直的，这只是K形节点中一般情况的一个特例，实际上，按三个平面两两之间的关系，K形节点的相交情况应有如下3种：

(1) 三根杆件组成的一个平面；

(2) 三根杆件组成三个平面，其中两个相互垂直；

(3) 三根杆件组成三个平面，均相互不垂直。

情况(1)是三根杆件组成了一个平面，此时 K形节点处的相贯线计算方法与T形节点相同，但需要进行两次T形节点相贯线的计算，同时，两次计算的相贯线不会相交。

情况(2)为本文讨论的情况，情况(3)是情况(2)的一般化，如图6所示，杆件r3的绕x1轴从r1的位置旋转2α至图中虚线3r′位置后，再绕1y′轴旋转一个角度3α至图中r3位置，由此可知，其相贯线的计算方法是在情况(2)的基础上对r3杆件多进行一次绕1y′轴的旋转变换计算即可。该情况下杆件r2和 r3的 z坐标求解过程仍为二次方程的计算求解，在此不再详述。

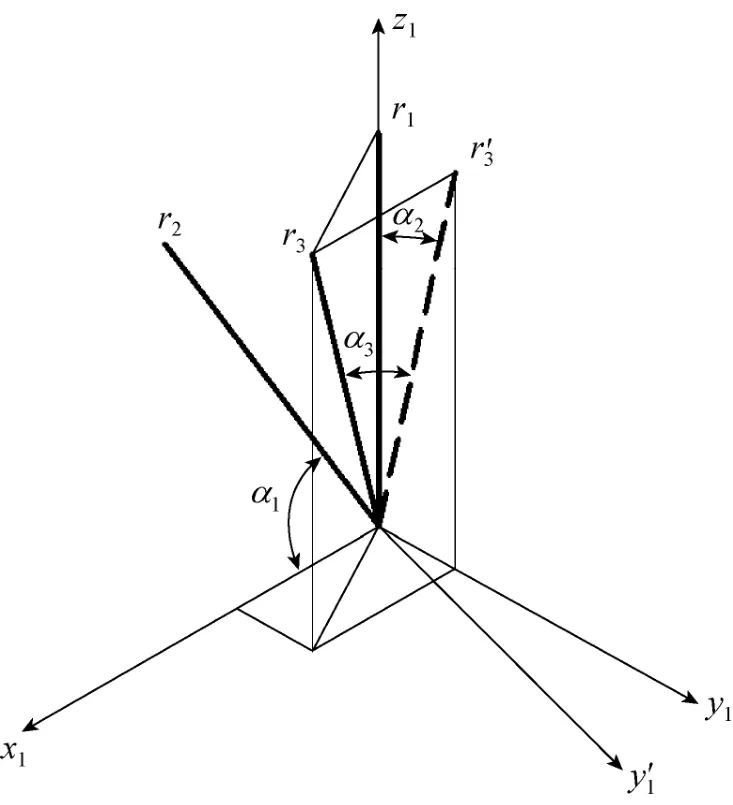
图6 第3种情况下的K型节点

如果结构模型在设计时，杆件之间有特殊角度，如90°，其正弦和余弦值都可直接按计算值先行带入公式，以减少计算量。如采用程序计算，则可直接按设计条件输入。

3 模型制作

在制作模型过程中，不必将杆件沿相贯线裁剪，这样不利于杆件的粘结，可将杆件沿相贯线裁剪成条状，如图 7所示，然后将这些纸条作为粘结端与其他杆件包裹粘贴，图 8所示为按该方法制作的K形节点。在构件制作过程中，如果有直径大小不同的杆件组成的节点，应保证直径较大杆件的完整性，对较小的杆件进行裁剪。

图7 杆件剪裁

图8 K形节点模型

比较不同方法制作的模型重量，使用相贯线裁剪的方法制作的模型质量为136.5 g，未使用该方法制作的模型质量为 157.4 g(河南省大学生结构模型竞赛数据)，效果明显。在承载能力方面，使用相贯线裁剪方法制作的模型都达到了比赛要求的上限(50 kg)，继续加载后，模型破坏均由杆件屈曲造成，节点未出现先破坏的情况。同时，由于节点的外形和质量都得到了减小，结构传力途径也得到了进一步的明确，模型整体破坏的部位与软件分析的结果接近。

4 小 结

本文针对结构模型竞赛中常见的节点处理问题，通过分析模型制作过程中常见的T形和K形节点杆件相贯的情况，构建了这两种节点下圆管相贯线展开的一般数学模型，并编制计算程序，为模型设计和制作提供了有利手段。通过竞赛结果证明：该方法在保证模型承载能力的前提下能较大幅度地减少模型重量。

[1]金伟良. 第一届全国大学生结构设计竞赛作品选编[M]. 北京： 中国建筑工业出版社, 2006： 63-64.

[2]陈庆军. 第1～6届全国大学生结构设计竞赛回顾[EB/OL]. [2012-10-31]. http：//202.38.193.234/hntjg/index. aspx.

[3]夏巨谌, 陈国清, 王 英, 等. 实用钣金工[M]. 北京：机械工业出版社, 2000： 16-24.

[4]郝立华, 孟 政. 基于斜投影变换研究画法几何中相贯线图解[J]. 沈阳师范大学学报： 自然科学版, 2014, 32(1)： 65-67.

[5]赵 龙, 郭艳玲. 基于OpenGL的相贯线切割轨迹的建模与仿真[J]. 工程图学学报, 2010, 31(2)： 198-203.

[6]季 忠, 刘 韧. 管管相贯数学模型及其在数控加工中的应用[J]. 工程图学学报, 2002, 23(2)： 139-144.

[7]张晓东, 王园宇, 郝鹏飞, 等. 相贯线及其展开曲线的方程构建方法的研究[J]. 机械设计与研究, 2008, 24(2)：21-24.

Using Developmental Figure of Intersecting Line to Make Structure Model

He Dazhi, Zhao Yanxia, Yan Leiyuan
(School of Civil Engineering and Communication, North China University of Water Resources and Electric Power, Zhengzhou Henan 450011, China)

Weight is an important indicator to evaluate a model in structure model design contest. Intersecting curve cutting is an efficient way to save material content. This method is widely used in plate work. In this paper, how to use the method of intersecting curve cutting to make paper structure model is discussed. Two cases are analyzed that is two intersecting pipes and three intersecting pipes. The geometric relationship and coordinate transformation are used to derive the expansion formula. The developed curve of intersecting curve can be drawn accurately and conveniently. Practice of model-making process shows the model has been greatly optimized in weight.

structure model; joint; intersecting line; developmental curve figure; coordinate transformation

TB 23

A

2095-302X(2015)01-0012-05

2014-06-13；定稿日期：2014-07-25

华北水利水电大学高层次人才科研启动资助项目；华北水利水电大学本科教学工程资助项目

何大治(1977-)，男，河南洛阳人，副教授，博士。主要研究方向为工程图学应用与计算机仿真。E-mial：hdz@ncwu.edu.cn