可控性的双层粒子刚体脆性破裂模拟动画

陈沸镔， 王长波， 谢步瀛

(1. 同济大学建筑工程系，上海 200092；2. 华东师范大学软件学院，上海 200062)

可控性的双层粒子刚体脆性破裂模拟动画

陈沸镔1， 王长波2， 谢步瀛1

(1. 同济大学建筑工程系，上海 200092；2. 华东师范大学软件学院，上海 200062)

提出一种可控性的双层粒子模型的刚体脆性破裂动画的模拟框架。首先，使用接触力学分析撞击时固体内部产生的弹性位移并采用光滑粒子流体动力学进行离散求解，在此基础上建立一个可控性的内力分析模型。其次，提出一种双层粒子模型来对刚体进行建模，在保证内力计算精度的同时提高了刚体动力学中碰撞检测的效率。最后实现了多个刚体脆性模型场景的动画。该算法可适用于刚体脆性破裂模拟的动画应用。

可控性模型；双层粒子；刚体脆性破裂模拟；光滑粒子流体动力学

固体的脆性破裂是一种常见的自然现象，如摔碎的瓷器、玻璃的碎裂等。表现这些现象并进行真实感绘制，在游戏动画、影视特效等领域有着重要的应用。在计算机图形学领域，脆性破裂的模拟已经引起了许多研究人员的注意，并做了许多工作。然而，现有的脆性破裂模拟方法仍然有值得改进的地方。首先，对于脆性破裂的力学分析往往直接采用了连续介质力学的方法，计算的结果虽然有较高的精度然而模拟的结果比较单一，缺乏对动画模拟的可控性；其次，在大型场景的模拟时，大量的刚体运动和碰撞受力计算对于模拟系统会造成比较大的计算量，如何提高系统的运行效率也是值得改进的一个方面。

针对固体脆性破裂的特点，本文提出了一种具有可控性的双层粒子的刚体脆性破裂模拟算法，能够有效地对模拟结果进行控制并提高计算的效率。该方法能有效处理刚体受到撞击后发生的破裂现象，使其有效地应用于动画以及影视特效模拟中。

1 相关工作

对于脆性破裂的模拟最早可以追溯到上世纪80年代。Terzopoulos等[1-2]将固体表示成网格，将开裂的模拟假定为弹性受力问题并使用了有限差分法进行计算，类似的研究工作还有Norton等[3]。这些早期的固体脆性破裂模型的共同点是采用了弹簧-质点模型对固体进行建模，将固体的质量集中在各个质点上，并使用弹簧来模拟质点间的受力。这类模型简单且计算速度快，但计算开裂点时其精度较低，无法准确地确定裂纹尖端，对于各项异性材料的模拟也有较大的难度。为了克服弹簧-质点模型的缺点，研究人员从力学上借鉴了很多更为精确的模型。在工程领域作为一种基于网格的方法，有限元(finite element method，FEM)在模拟变形和破裂方面已经被证明是一种具有较高精度的数值模型。因此在图形学领域，有限元方法最早由O＜ Brien等人所引进用来模拟脆性破裂[4]和塑性破裂[5]，是将固体离散成一系列的节点和单元，由外部撞击产生的内力通过对一个由所有节点的属性组成的大型线性方程组进行求解计算而得到的。这种直接求解线性方程组的计算量是比较高的，而在图形学领域中的模拟往往不需要如此高的精度，因此可以进行一定程度地简化，如将撞击问题假定为准静态问题[6-7]。

在力学及工程领域，相对于基于网格的力学模型，近年来人们更关注的是无网格方法，即稳定且精度较高的数值方法。无网格方法使用粒子对求解区域进行离散建模，其求解不受网格的约束因而有较大的灵活性，对于开裂这一类求解区域不连续的问题有着较好地应用。在图形学领域，最早使用无网格方法进行固体模拟的是Desbrun和Cani[8]。光滑 粒 子 流 体 动 力 学 (smoothed particle hydrodynamics，SPH)作为一种无网格方法，已经应用在流体模拟[9]，颗粒介质模拟[10]和固体变形模拟[11]方面。在固体破碎模拟方面，目前采用无网格方法进行破碎模拟的有无网格局部 petrov-galerkin法(meshless local petrov-galerkin，MLPG)[12]和移动最小二乘法(moving least squares，MLS)等方法[13]，而SPH模型尚未应用到固体破碎模拟上。

从几何学角度看，开裂的模拟实际上是一个网格的分解，这涉及到对一系列三角形或者四面体进行切割，即一个曲面模型的分解与合并的计算，在计算代价上，只在网格的节点上进行分解操作比直接切割网格的计算效率要高，因此许多模型均采用在节点上进行分解操作，如四面体网格模型[6]、规则八面体网格模型[14]、Molino等[15]提出的虚节点算法等，均是在对原始的几何模型采用Voronoi图的网格剖分后进行了一定的约束限制再进行网格的分解操作。最近，Müller等[16]提出了一种凸包的近似分解算法(volumetric approximate convex decomposion，VACD)可以在实时的程度上进行三角形的切割操作。总而言之，一种有效的几何模型在破碎模拟上有着很重要地应用。

在计算机图形学领域，对于一个模拟算法而言，如何在模拟规模比较大的时候提高计算效率是一个很重要的问题。对于一个粒子系统而言，在求解问题规模较大的时候效率往往是系统的一个瓶颈。针对这个问题，近些年研究人员也提出了许多方法，其中包括双层/多层粒子建模技术。双层/多层粒子的核心思想是在一个框架中通过采用不同尺度粒子同时对同一区域进行离散建模，从而产生不同层次的粒子，各层次的粒子在框架中的作用各不相同，该模型已经应用到固体形变模拟[17]、流体模拟[18]、颗粒物质(沙子)模拟[19]等，而在固体破裂模拟方面却很少见到，从双层/多层粒子模型的特性来看，其应用于固体脆性模拟具有很大的优势。

2 固体脆性模拟框架

2.1 弹性接触模型

为了使用基于物理的方式进行固体脆性模拟，必须建立一种合适的力学模型来分析撞击产生的应变和应力，与以往采用的基于连续介质力学模型不同，为了提高模拟结果的可控性，本文采用了基于接触力学的物理模型[20]。假定两个物体之间产生了碰撞，首先将碰撞力分解为两个方向的力：与接触面所垂直的法向力P和与接触面平行的切向力Q。以碰撞点O为坐标中心，建立一个坐标轴Oxyz，其中Oz的方向是与接触面垂直的法向。根据接触力学[20]中的势能理论(由Love提出)，由于碰撞力P在碰撞点O产生弹性位移可以表示为：

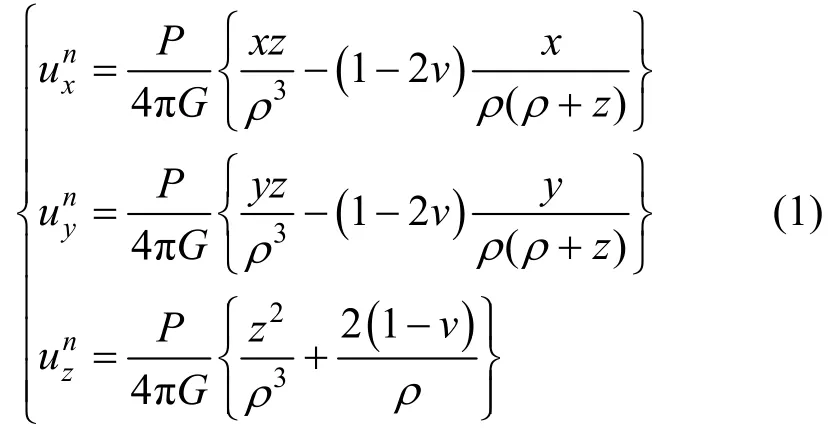
同时，将切向力在碰撞点产生的弹性位移tU在 Ox和Oy轴上进行分解，在Ox轴方向上的弹性位移可以表示为：

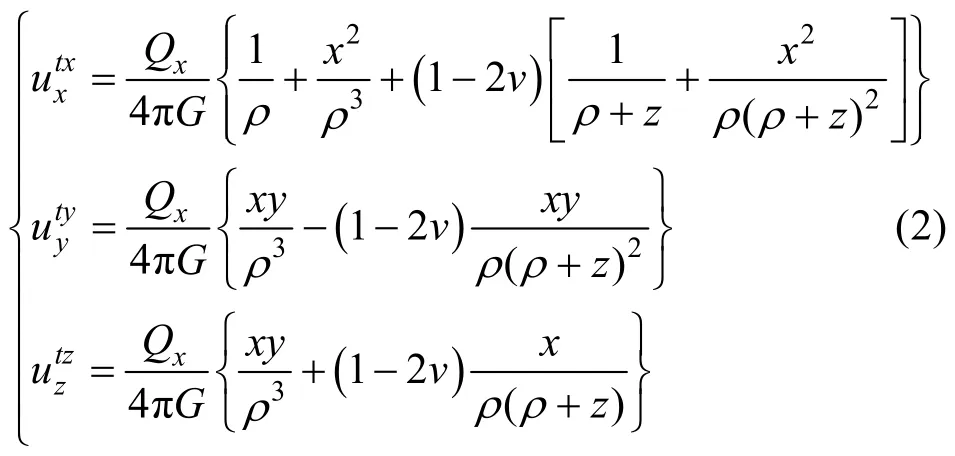
式(1)～(3)给出了总弹性位移U，总接触力P Q+ 以及固体内部任意一点到接触点的距离ρ之间的关系，从上述公式中可以看出，在物体之间产生撞击时，其接触力越大，产生的弹性位移越大，离接触点的距离越远，则弹性位移越小。使用上述公式能在碰撞时对接触域内任意点的位移进行求解计算，从而得到整个物体内部的位移场，在得到位移场后，根据green-saint-venant应变ε的定义，可以得到：

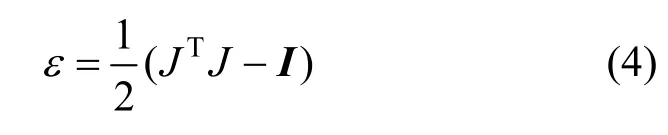
其中，I是单位矩阵，TJ u=∇ ， u∇ 是位移的梯度场，根据线弹性材料的虎克定律[21]，应力σ可表示为：

其中，C是一个由材料特性决定的6阶方阵。

2.2 光滑粒子流体动力学的数值离散

SPH是一种无网格数值方法[22]，其核心是用一系列分散的粒子对问题区域中的某一个物理量进行求解，如位移、速度、应力等。求解区域中任意一个点的物理量值是由其支持域中所有邻接粒子所对应的值来进行加权求和得到。

在SPH中，任意连续的物理场〈 〉f 在某个位置i的物理量值〈 fi〉可以由其支持半径 h所定义的支持域中所有邻接粒子对应的属性值使用核函数 W( xij,h)来进行加权求和得到：

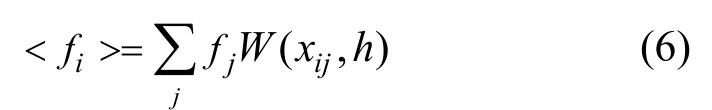
其中， xij是该求解点与邻接粒子之间的距离。核函数 W( xij,h)通常取为具有归一、对称、非负的光滑函数。可以利用上式对上节的位移梯度场 ∇ u进行离散求解：

其中， mj和 ρj分别是粒子j质量和密度，uji= uj- ui，ui和 uj分别是由式(3)计算得到的粒子i和j位置处的位移。

2.3 可控性的内力分析模型

在动画和电影特效的制作过程中，制作人员往往需要根据所绘场景的需要对模拟结果进行调整，如控制模拟物体运动的速度，调整物体运动的位移等。在破裂模拟中，模拟模型是否能对破碎的结果进行一定控制，并使模拟的结果具有可控性，是其应用价值所在。合适的模型动画制作人员通过几个参数就可以对模拟的结果进行人为干预，并得到预期的结果。针对这个问题，本节提出一种具有可控性的内力分析模型。

为了模拟固体的开裂，需要选择一定的材料屈服准则来确定开裂点以及开裂法向。对于脆性模拟，可以选择经典的Rankine准则[23]：当固体内部某个点的主应力超出了某个指定的阈值时，材料达到屈服，发生开裂，其开裂面的法向为主应力的方向。

计算主应力的方向和大小时，先根据2.1节中的公式通过接触力大小(这里的接触力是由刚体动力学计算得到的)来计算位移场，再使用2.2节中的SPH式(7)计算位移的梯度场，最后根据式(4)和(5)可以得到应力的大小和方向。

本文使用 SPH数值离散方法来计算位移的梯度场。SPH方法的一个重要特性是某个位置的值是由其邻接粒子相应的值所决定的。从式(7)可以看出，某个位置位移的梯度是通过该点的邻接粒子位移值的加权求和计算的。如能选择性地使用邻接粒子的位移来计算该点的位移梯度值，所得的应力主方向必然是不相同的，在模拟的结果上表现为同一点产生多条不同的裂缝。尽管从数值方法的角度上说此方法无法保证精度，然而从图形学的角度来看，却能达到人为干预裂缝生成的要求。图1是内力分析的过程，具体的内力分析流程如下：

对某个应力分析点：

获得在SPH光滑半径内的邻接粒子对所有的邻接粒子：

计算与分析点间的距离

根据人为设定的裂纹数量n进行分组对于每个邻接粒子组：

使用式(3)～(5)计算应力大小得到n个应力

对于计算的每个应力：

计算应力张量的大小maxd 及方向

如果： max threshold

d d＞

材料达到屈服极限，产生裂纹

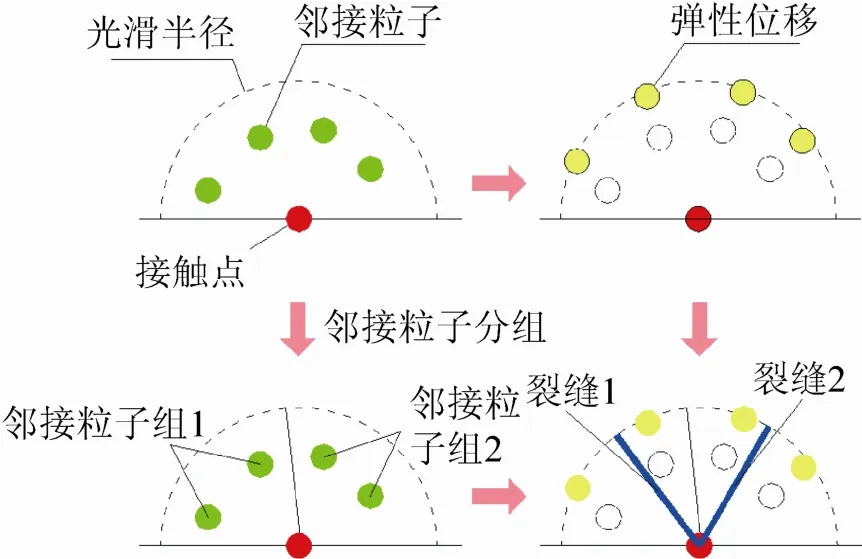
图1 内力分析示意图

3 双层粒子模型

如图2所示，本文提出了一种双层粒子的模型来对固体的运动过程进行模拟，通过将其离散成两个不同层次的粒子(物理层粒子边界层粒子)来分别进行内力分析和动力学计算。从而在保证模拟细节的同时提高了模拟的效率。

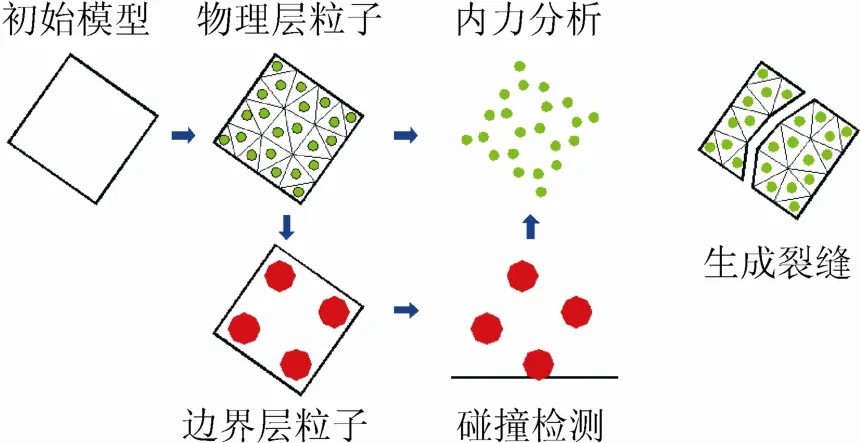
图2 双层粒子模型示意图

3.1 物理层粒子

力学分析模型是采用 SPH方法进行内力分析计算的，因此，需将原始的固体模型离散成一系列的粒子。使用文献[23-24]中的方法对固体进行离散建模，首先将固体离散成一系列的四面体，再根据四面体生成相应的粒子。在四面体离散算法上，采用了 Delaunay网格[25]计算对初始的固体模型进行四面体网格化。具体模型的粒子化过程可见图3。

图3 物理层粒子生成过程示意图

初始的固体模型通过 Delaunay三角化算法得到一个整体的四面体网格；在每个四面体的形心分配一个粒子，其质量等于四面体的质量，粒子的半径 r是由相应四面体体积 V计算得到的：为了避免开裂处理时网格维护几何拓扑的计算开销过大，使用了文献[24]中基于约束的方法进行几何网格的切割操作，从而能够有效地减少计算代价。

在刚体动力学计算时，直接采用上述物理层的粒子进行碰撞检测是一个简单而有效的方式。然而，为了保证内力分析时的计算正确性，物理层的粒子尺度往往需要比较小，在碰撞检测过程中会增加计算代价。当模拟的场景规模比较大时，大量的粒子碰撞检测会降低模拟计算的速度。为了解决这个问题，在物理层粒子的基础上额外建立一个边界层的粒子用来进行刚体动力学检测的运算。

3.2 边界层粒子

将物理层的粒子分为两类：内部粒子和表面粒子，内部粒子是位于固体内部，而表面粒子是位于固体表面。在碰撞检测时，可使用表面粒子进行碰撞检测计算。但是直接采用表面粒子进行碰撞检测计算会受制于物理层粒子的离散尺寸。为了提高检测效率，在固体表面的物理层粒子的基础上，需建立一个边界层的粒子用来进行碰撞检测。

边界层粒子的计算过程见图4。一个由用户定义的采样数量n被引入，本文实验将采样数量定为4。在所有的边界粒子中，将每n个物理层表面粒子合并为一个边界层粒子，每个边界层粒子的质量与其所对应的物理层表面粒子的总质量相等，其位置为n个物理表面层粒子。在边界层粒子的生成过程中，可以发现有些物理层表面粒子(如位于固体表面比较尖锐处的粒子)无法被合并成一个边界层粒子，这个问题可以有两种解决方法：直接使用这些粒子作为边界层粒子，或者将这些粒子忽略。

当使用边界层粒子进行碰撞检测时，在动力学计算的每个时刻，所有边界层粒子的位置都会随着刚体的运动而改变，因此便于下一步碰撞检测。只有在进行内力分析计算时，才会更新物理层粒子的位置来进行内力的分析计算，通过以上方法可以有效地提高计算的效率。

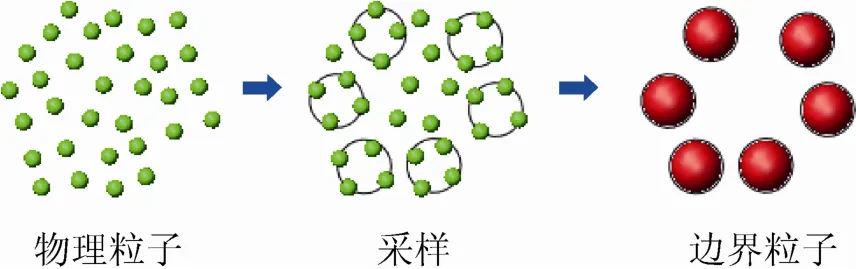
图4 边界层粒子采样示意图

4 算法的实现与结果分析

根据用上述章节提出的模拟框架，在Intel (R) Core i3-2100 (R) 3.2 GHz CPU、4 GB内存、NVIDIA GeForce GTX460 图形卡、1 GB显存的微机上进行模拟系统的算法编制，实现了多个刚体脆性模拟的场景，并采用3dmaxV-Ray对模拟结果进行离线渲染，以期达到真实感绘制的效果。固体模型的四面体 离 散 化 采 用 了 NETGEN 工 具(sourceforge.net/projects/netgen-mesher)进行生成。刚体动力学部分的算法在第三方物理引擎“Newton Game Dynamics” (newtondynamics.com)的基础上进行了一定的改进从而实现。

图5是一个圆环形瓷器下落摔碎的模拟场景，图 5(b)～(d)是使用本文内力分析模型进行开裂控制的结果，通过使用不同的邻接粒子组在同一个碰撞点进行开裂法向的计算可以得到不同的结果。

图6是一个较为复杂的场景的模拟，同时有13个圆环瓷器下落并破碎，对于每一个圆环，在内力分析时均采用了不同参数对裂纹生成进行控制。图7是3个玻璃墙受到撞击后连续破碎的效果。表1是图5～7不同场景模拟的复杂度统计表。

表1 不同场景模拟的复杂度统计

表2是本文方法在不同场景的物理计算时间的统计，由于使用了双层粒子的模型，在刚体动力学以及碰撞检测上的时间开销有了很大降低。

图5 圆环摔碎的模拟场景通过不同邻接粒子组来进行开裂法向的计算

图6 多个圆环摔碎的模拟场景

图7 3个玻璃墙被撞碎的模拟场景

表2 不同场景的物理计算时间的统计(ms)

5 总结与展望

本文提出了一种刚体脆性破碎的模拟算法。该算法具有如下特点：

(1) 该算法在接触力学和SPH数值方法内力分析的基础上进行了改进，提出了一种具有可控性的内力计算模型，从而能够达到对模拟结果进行用户交互控制的目的

(2) 针对粒子系统模拟效率的不足，提出了一种双层粒子的模型对固体进行建模，在保证模拟的精度上又提高了系统运行的效率。

本文的提出模拟框架还有一定的局限性，首先，无法模拟一些复杂的裂纹，如环形的裂纹，需要在现有的内力分析模型上做进一步地改进。其次，双层粒子的采样算法需要进行进一步的优化使得能够支持复杂的几何模型。

未来的工作包括：采用 GPU技术应用到文中的算法上，将算法扩展到塑性破裂模拟上，进行更为复杂场景的模拟。

[1]Terzopoulos D, Platt J, Barr A, et al. Elastically deformable models [C]//Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, California, USA, 1987： 205-214.

[2]Terzopoulos D, Fleischer K. Modeling inelastic deformation： viscolelasticity, plasticity, fracture [C]// Proceedingsof the 15th Annual Conference on Computer Graphics and Interactive Techniques, Atlanta, Georgia, USA, 1988： 269-278.

[3]Norton A, Turk G, Bacon B, et al. Animation of fracture by physical modeling [J]. The Visual Computer, 1991, 7(4)： 210-219.

[4]O′Brien J F, Hodgins J K. Graphical modeling and animation of brittle fracture [C]//Proceedings of the 26 th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ＇99, Los Angeles, California, USA, 1999： 137-146.

[5]O＇ Brien J F, Bargteil A, Hodgins J K. Graphical modeling and animation of ductile fracture [J]. ACM Transactions on Graphics, 200, 21(3)： 291-294.

[6]Müller M, McMillan L, Dorsey J, et al. Real-time simulation of deformation and fracture of stiff materials [C]// Proceedings of the Eurographic Workshop on Computer Animation and Simulation, Manchester, UK, 2001：113-124.

[7]Bao Zhaosheng, Hong J M, Teran J, et al. Fracturing rigid materials [J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(2)： 370-378.

[8]Desbrun M, Cani M P. Space-time adaptive simulation of highly deformable substances [R]. Rapport de Recherche RR-3829, INRIA (1999).

[9]Müller M, Charypar D, Gross M. Particle-based fluid simulation for interactive applications [C]//Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, California, USA, 2003： 154-159.

[10]Alduan I, Otaduy M A. SPH granular flow with friction and cohesion [C]//Proceedings of the 2011 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Vancouver, British Columbia, Canada, 2011：25-32.

[11]Becker M, Ihmsen M, Teschner M. Corotated SPH for deformable solids [C]//Proceedings of the Fifth Eurographics conference on Natural Phenomena, Munich, Germany, 2009： 27-34.

[12]Liu Ning, He Xiaowei, Li Sheng, et al. Meshless simulation of brittle fracture [J]. Computer Animation and Virtual Worlds, 2011, 22(2/3)： 115-124.

[13]Pauly M, Keiser R, Adams B, et al. Meshless animation of fracturing solids [J]. ACM Transactions on Graphics, 2005, 24(3)： 957-964.

[14]Müller M, Teschner M, Gross M H. Physically-based simulationof objects represented by surface meshes [C]// Proceedingsof the Computer Graphics International, Hersonissos, Crete, Greece, 2004： 26-33.

[15]Molino N, Bao Zhaosheng, Fedkiw R. A virtual node algorithm for changing mesh topology during simulation [J]. ACM Transactions on Graphics, 2004, 23(3)： 385-392.

[16]Müller M, Chentanez N, Kim T Y. Real time dynamic fracture with volumetric approximate convex decompositions [J]. ACM Transactions on Graphics, 2013, 32(4)： 115：1-115：10.

[17]Adams B, Pauly M, Keiser R, et al. Adaptively sampled particle fluids [J]. ACM Transactios on Graphics, 2007, 26(3)： 115-120.

[18]Solenthaler B, Gross M. Two-scale particle simulation [J]. ACM Transactios on Graphics, 2011, 30(4)： 81：1-81：8.

[19]Ihmsen M, Wahl A, Teschner M. High-resolution simulation of granular material with SPH [C]// Proceedings of Workshop on Virtual Reality Interaction and Physical Simulation, Darmstadt, Germany, 2012：53-60.

[20]Johnson K. Contact mechanics [M]. Cambirdge：Cambridge University Press, 1985： 108-112.

[21]Fung Y. A first course in continuum mechanics [M]. Englewood Cliffs, N.J： Prentice-Hall, 1969： 75-95.

[22]Liu M B, Liu G R, Smoothed particle hydrodynamics (sph)： an overview and recent developments [J]. Archives of Computational Methods in Engineering, 2010, 17(1)：25-76.

[23]Gross D, Seelig T. Fracture mechanics： with an introduction to micromechanics [M]. Springer Verlag, 2006： 42-52.

[24]Smith J, Witkin A, Baraff D. Fast and controllable simulation of the shattering of brittle objects [J]. Computer Graphics Forum, 2001, 20(2)： 81-90.

[25]Chen Siuwing, Dey T K, Shewchuk J. Delaunay mesh generation [M]. Boca Raton, Florida： CRC Press, 2012：1-8.

Controllable Two Scale Particles for Fracture Animation of Brittle Materials

Chen Feibin1, Wang Changbo2, Xie Buying1
(1. Department of Architectural Engineering, Tongji University, Shanghai 200092, China; 2. Software Engineering Institute, East China Normal University, Shanghai 200062, China)

A controllable two scale particle framework for simulate the brittle fracture is presented. Firstly, the elastic displacement induced by the collision between two rigid bodies is analyzed based on contact mechanics and solved by using of smoothed particle hydrodynamics, and a stress analysis model is proposed to control the result of simulation. Secondly, a two scale particle model is introduced to present the rigid; this two scale particle system serves for the purposes of more accurate fracture modeling and more effective collision handling. Finally, rendering the fracture of brittle material is achieved in some scenes. Our method can apply for simulating the fracture of brittle material.

controllable model; two scale particles; simulation of brittle fracture; smoothed particle hydrodynamics

TP 391.1

A

2095-302X(2015)01-0111-06

2014-08-11；定稿日期：2014-08-20

国家自然科学基金面上资助项目(61272199)；教育部博士点基金资助项目(20130076110008)；上海市教委科研创新项目重点资助项目(12ZZ042)

陈沸镔(1983-)，男，福建南平人，博士研究生。主要研究方向为基于物理的仿真、流体模拟。E-mail：feibin.chen@gmail.com

王长波(1976-)，男，湖北随州人，教授，博士。主要研究方向为计算机图形学、虚拟现实等。E-mail：cbwangcg@gmail.com