燃气轮机仿真中部件特性处理方法的准确性研究

孙 博，彭淑宏，吴克梁

（上海电气燃气轮机有限公司，上海201612）

燃气轮机仿真中部件特性处理方法的准确性研究

孙 博，彭淑宏，吴克梁

（上海电气燃气轮机有限公司，上海201612）

在基于部件的燃气轮机性能仿真建模过程中，部件特性线处理方法的准确性是影响整个机组仿真精度的关键因素。分别介绍了采用传统离散插值处理方法、人工神经网络法和偏最小二乘法进行部件特性线处理的原理和方法，利用一部分已知样本特性数据和不同处理方法对某燃气轮机进行性能仿真，并将仿真结果与另一部分已知样本特性数据进行比较，分析不同处理方法对部件特性和整机性能计算精度的影响。结果表明：在仿真过程中利用偏最小二乘法可直接使用重构方程求解部件特性，无需对部件特性离散化和插值处理，避免了传统部件特性处理方法的计算误差，提高了燃气轮机热力模型求解的精度。

燃气轮机；性能仿真；特性线；建模；处理方法

符号表

IGV 进口可调导叶

n*C压气机相对折合转速

π*C压气机相对压比

m*压气机相对折合质量流量

ηC压气机相对等熵效率

n*Τ涡轮相对折合转速

πΤ涡轮相对压比

m*T涡轮相对折合质量流量

ηT涡轮相对等熵效率

角标

C 压气机

T 涡轮

0 设计工况

* 滞止/总参数

0 引言

燃气轮机是由包括涡轮、压气机、燃烧室等多部件组成的复杂的成套动力机械装备。对燃气轮机进行变工况性能预测仿真过程中涉及到对部件特性的描述，特别是对压气机和涡轮这样的关键部件而言，特性曲线的描述和处理方法关系到整个仿真计算的准确性。对现代重型燃气轮机轮机而言，压气机具有高压比及进口可调导叶（IGV），而涡轮冷却设计复杂，其部件特性曲线的描述过程和描述方法也更为复杂，因此有必要对关键部件特性处理方法作详细地分析研究。

部件特性建模方法有多种，传统方法是将部件特性线离散为数组形式，并在仿真过程中以插值方式进行变工况特性匹配。随着现代计算机技术的发展，许多新技术应用到燃气轮机仿真过程中。Changduk Kong[1]将遗传算法应用于燃气轮机压气机特性图的重构计算，并将仿真结果与传统模型方法及试验数据进行比较，证明了该方法的可行性；尹大伟[2]使用基于空间分布权系数邻域选点的Kriging方法计算了压气机变工况特性，证明其优于传统插值方法；Wang Zhiao，M Gholamrezaei，K.Ghorbanian等[4-7]将人工神经网络技术引入部件特性模拟，比较了广义回归网络（the rotated general regression）和多层感知器神经网络的特性线处理方法的精度和优缺点。

以导叶不可调的压气机为研究对象已不能满足现代重型燃气轮机的仿真需求；传统的部件特性线拟合插值方法计算精度差，而神经网络又存在泛化能力差的问题。本文针对以上问题，提出了采用偏最小二乘法PLS（Partial least square regress，偏最小二乘回归方法）[10]对压气机和涡轮2个部件进行特性重构，比较了各种工况下偏最小二乘法、传统插值方法、人工神经网络法的部件特性计算精度。以某燃气轮机为例，利用ISPEpro过程分析软件，建立了该燃气轮机的稳态仿真模型，经过计算，比较分析了使用不同部件特性线处理方法对燃气轮机整体热力性能精度的影响。

1 部件特性常用处理方法

压气机和涡轮的特性通常是将其主要参数，包括IGV开度、转速、压比/膨胀比、流量和效率等，以无因次折合参数的形式，绘制成为流量特性线和效率特性线。在燃气轮机仿真过程中，需要将这些特性线以特定的处理方法放入部件模型，并联立其他的控制方程求解，本文针对几种常用处理方法展开讨论。

1.1 传统方法

对部件特性线进行处理的传统方法常常是把部件特性线离散化，以数组表格的形式放入部件模型中，在求解时采用插值方法获得部件变工况特性。这种方法最关键的2步是离散化和插值，其优点是使用方便，但也存在以下问题：

（1）在对特性线进行离散化时，不可避免的带来部件特性的信息缺失，可能无法正确表达特性线的形状；

（2）特性图中各等转速线的压比范围不同，但以2维表格的形式处理特性线时则要求各转速下的范围一致，给表格表达带来困难；

（3）压比较小时，等转速线上流量呈近似垂直直线，在制作离散化表格时，很难准确捕捉到流量随压比的微小变化。

因此在传统特性线处理过程中，特性线表格与实际特性线之间存在着不可避免的偏差。另外，传统方法采用表格线性插值或样条插值的方法求取部件变工况特性。当插值点不在表格节点上时，计算要经过多次插值，带来工作量增大、精度降低等问题。

1.2 神经网络法

神经网络法在部件特性方面有较多应用[8-9]，被采用的神经网络类型多样，但基本原理类似。一般来说，神经网络法特性线拟合是将已有特性线数据作为学习样本，经过训练后建立起部件特性的神经网络模型。以压气机为例，具体表达如下

式中：Y为{效率，流量}；X为{IGV，转速，压比}。

训练好的神经网络f（）即可用于求解不同X参数下的部件的变工况特性Y，可有效避免插值误差，但也存在以下问题：

（1）学习过程需要大量的样本数据，才能训练出精确反映特性线形状的神经网络。

（2）由于泛化能力较差，对已有样本区域以外的点，计算精度差甚至会大大偏离实际值。

1.3 回归分析法——偏最小二乘法PLS

PLS是从化工领域发展起来的1种新型多元数据统计分析方法，于1983年由伍德（S.Wold）和阿巴诺（C.Albno）等首次提出。集多元线性回归分析、典型相关分析和主成分分析的功能为一体，将建模预测类型的数据分析方法与非模型式的数据认识性分析方法有机结合起来[11-12]。其建模机理如下：设有2组变量，p个自变量{x1，x2，…，xp}和q个因变量{y1，y2，…，yq}，进行了n次采样得到样本点n个，构成自变量数据表X=[x1，x2，…，xp]n×p与因变量数据表Y=[yi1，yi2，…，yiq]n×p。偏最小二乘法分别在X和Y中提取成分t1和u1，t1和u1分别是x1，x2，…，x p和y1，y2，…，yq的线性组合，并且t1和u1需满足：应尽可能多地携带各自数据矩阵中的变异信息；t1和u1的相关程度能够达到最大。

在第1个成分t1和u1被提取后，偏最小二乘法分别实施X对t1的回归以及Y对t1的回归，如果回归方程已经达到满意的精度，则算法终止；否则，将利用X被t1解释后的残余信息以及Y被t1解释后的残余信息进行第2轮成分提取。如此循环，直到达到较满意的精度为止。若最终对X共提取了m个成分t1，t2，…，tm，偏最小二乘法将通过实施yk对t1，t2，…，tm的回归，然后再表达成yk关于原变量x1，x2，…，xp的回归方程，k=1，2，…，q，至此偏最小二乘建模完成。

偏最小二乘回归法用最简单的方法求得一些绝对不可知的真值，而令误差平方之和为最小。主要有以下优点：

（1）能够在自变量存在严重多重相关性的条件下进行回归建模；

（2）偏最小二乘回归模型更易于识别系统信息和噪声；在偏最小二乘回归模型中，每个自变量的回归系数更容易解释，通常用于曲线拟合。

2 基于偏最小二乘法定部件特性重构和建模

燃气轮机在低转速尤其是起动工况运行时，由于空气流量小于设计值，前几级压气机很容易因强烈的旋转脱离而进入喘振工况[13-16]。在现代燃气轮机设计中，为了改善压气机喘振特性和燃气轮机低负荷性能，通常会采用进口可调导叶（IGV）。

在压气机空气流量变化或者变工况条件下，压气机轴向速度与圆周速度的配合关系不协调时，可以关小或者开大可变导叶的安装角度γ，使气流绝对速度C1的方向变化，消除偏离设计值的正负冲角，以保证气流进入动叶的相对速度W1的方向恒定不变，达到防喘振的目的。同时，导叶安装角γ的变化，会使压气机特性线向左或者向右移动。

可见，对于进口导叶可调的压气机，表示工作性能的主要参数除了压比、效率、流量、转速和进气的压力及温度外，还有IGV。为了解决变工况和数量级差异，采用通用特性进行描述，即将压气机的通用特性用IGV、相对折合流量、相对折合转速、相对压比和相对效率5个参数表示，相比导叶固定不可调压气机多了1个参数——IGV。只要其中任意3个参数确定，那么压气机就有1个完全确定的工作状态，因此压气机运行工况的独立参变量有3个。压气机的通用特性可表达为

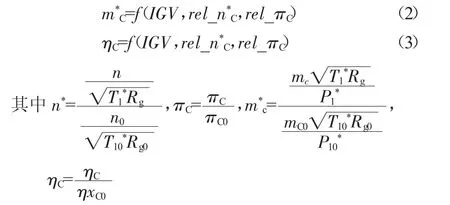
式中：n为转速；T1为压气机进口总温；Rg空气气体常数；πc压气机压比；mc为压气机进口流量；p1*为压气机进口总压；ηc为压气机效率。

压气机特性重构时，将IGV，nc*，πc，mc*和ηc进行组合，将前3个参数作为自变量进行线性回归分析，即采用3元偏最小二乘法PLS-3，得到压气机特性线的3元偏最小二乘法回归模型

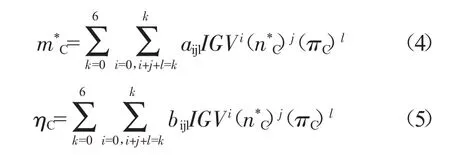
可调进口导叶压气机特性由一系列φIGV（为进口可调导叶开度）下的几组等折合转速特性线表示。如果将各φIGV下的特性线分别用2个参数作为自变量进行独立重构，并将得到的特性在不同φIGV所对应的曲线之间进行插值，也可以满足热力模型中对压气机特性计算的需求。在这种情况下可将各φIGV下的相对折合转速、相对压比、相对折合流量和相对效率组合，将相对折合转速、相对压比作为自变量进行线性回归分析，即采用2元偏最小二乘法PLS-2，得到压气机特性线的2元偏最小二乘法回归模型

对于涡轮来说，其特性线处理方法与不包含φIGV的压气机特性线回归模型相似，不同的是主要参数为膨胀比πc、效率ηc、流量mc、转速n和进气的压力p3*及温度T3*，表示为通用特性参数mT*、nT*、πT和ηT4个参数。

进行涡轮仿真时，将通用特性参数进行组合，将相对折合转速和相对膨胀比作为自变量进行线性回归分析，得到涡轮特性线的偏最小二乘法回归模型

利用偏最小二乘法进行部件特性重构后，可将重构方程直接放入部件模型中，当压气机采用PLS-2，在变工况计算时，要经过1次关于φIGV的插值计算。压气机采用PLS-3和涡轮采用PLS-2，在变工况计算时，直接采用数学方法计算工作点，无需插值。

3 不同部件建模方法比较

3.1 不同建模方法对部件性能的影响

以某燃气轮机的压气机为例，通过利用已知的样本点对其特性线进行重构，比较采用传统方法、人工神经网络法和偏最小二乘法3种建模方法计算结果的精度。其中人工神经网络采用最典型的BP（Back Propagation，反向传播）3层神经网络，根据精度最高原则自动选取训练精度和隐层节点数。

在特性线重构过程中，使用了共705个特性样本点，φIGV范围为60.5%～100%，相对折合转速范围为0.75～1.10，相对压比范围为0.29～1.24，利用其中660个样本点作为3种建模方法的已知输入数据（称为原样本点），其余45个样本点作为验证数据（称为测试样本点），对3种不同的样本点进行比较：

（1）完全落在原样本点上的数据，即用于比较的重构数据与某些原样本点φIGV、相对折合转速和相对压比相同。

（2）落在已知φIGV上的数据，即用于比较的重构数据与某些原样本点φIGV相同，其他数据不同。

（3）3个变量均不存在对应值的数据，即用于比较的重构数据具有与原样本点不同的φIGV、相对折合转速和折合压比。

3.1.1 完全落在原样本上的数据比较

φIGV为100%，nc*=1时，3种方法建立的压气机流量重构特性线及原始样本点组成的压气机流量特性线比较如图1所示；该条流量特性线数据相对于原数据的相对误差如图2所示。φIGV为100%，nc*=1时，3条效率重构特性线及原始样本点组成的效率特性线如图3所示；该条效率特性线数据相对于原数据的相对误差图4所示。从图1～4的对比结果可见，对于正好落在原样本的数据点，PLS-2部件特性重构方法计算得到的结果误差最小，PLS-3计算得到的结果误差最大。但是3种部件重构方法计算结果相对误差绝对值均小于0.11%，由此可见，BP和PLS-2都能够很好地拟合原有数据点。

图1 压气机流量拟合比较

图2 压气机流量误差比较

图3 压气机效率拟合比较

图4 压气机效率误差比较

3.1.2 落在某个已有φIGV上的数据比较

可调导叶压气机的特性线是以不同φIGV下的几组特性线表示的。本文的原特性线样本中包含有φIGV=100的特性线数据。BP和PLS重构法计算得到的各不同转速和压比时的压气机流量和效率的相对误差如图5、6所示。

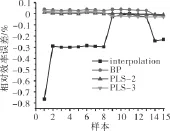
图5 φIGV=100%压气机效率误差比较

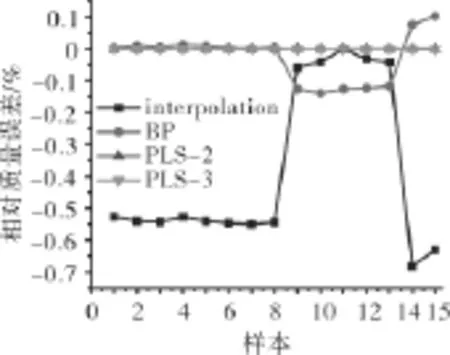
图6 φIGV=100%压气机流量误差比较

从图中可见，插值计算结果误差远大于其他3种方法；由于神经网络的泛化能力有限，BP计算得到的结果误差比采用PLS的大；对于正好落在已有φIGV上的数据，PLS-2不需进行关于φIGV的插值计算，PLS-2计算得到的结果相对误差最小，比PLS-3的计算结果误差低1个数量级。由此可见，对于正好落在某个已有φIGV上的数据点，PLS-2特性重构方法精度最高。

3.1.2 3个变量均不存在对应值的数据比较

使用1组与原样本完全不重合的测试样本进行重构流量和效率相对误差比较，如图7、8所示。采用插值法需要多次插值，采用PLS-2需做关于φIGV的1次插值计算，BP和PLS-3重构法则不需插值计算。从图中可见，插值计算结果误差最大；由于BP泛化能力差，个别点计算误差较大（如图8所示），稳定性不足；对于压气机效率，采用PLS-3计算结果误差比PLS-2的小，而对于压气机流量，采用PLS-2计算结果误差比PLS-3的小。因为本文采用的压气机特性样本数据不能覆盖全部φIGV和压比范围，使得部件重构中存在一定的形状辨识误差，导致采用PLS-3时压气机效率计算结果误差较大。

由于压气机流量误差对燃气轮机整机性能的影响大于压气机效率，因此，3个变量均不存在对应值的数据点，仍建议采用PLS-2，使得压气机特性误差对燃气轮机整机性能影响最小。

图7 压气机效率误差比较

图8 压气机流量误差比较

3.2 不同建模方法对燃气轮机整机性能的影响

由以上分析可知，在燃气轮机部件特性计算中，偏最小二乘法部件重构法具有显著优势。以某燃气轮机为研究对象，采用PLS-2和传统方法对压气机特性和涡轮特性重构，并在IPSEpro平台中建立起该燃气轮机的稳态模型，进一步比较2种方法对燃气轮机整机性能的精度影响。在不同环境工况（各环境工况压力均为1.01325 MPa），采用2种部件建模方法对燃气轮机轴功输出和热效率的误差影响比较如图9、10所示；在ISO工况下，不同负荷率和不同折合转速时2种部件建模方法对整机效率和轴功的误差影响比较如图11、12所示。

从图中可见，无论是不同环境工况还是同一环境工况不同运行点下，采用PLS部件特性重构方法都使整机轴功和热效率误差大大减小。因此，偏最小二乘法能够显著提高燃气轮机热力模型求解的精度。

图9不同环境下部件重构方法对轴功误差的影响

图10 不同环境部件重构方法对热效率误差的影响

图11 不同负荷率下部件重构方法对轴功的影响

图12 不同转速下部件重构方法对热效率误差的影响

4 结论

（1）在燃气轮机仿真中，相比传统方法和神经网络法，采用偏最小二乘法进行部件特性重构，能够提高燃气轮机部件特性求解精度和整机热力模型求解精度。

（2）对于还原样本数据点，BP神经网络和偏最小二乘法计算精度都较高；对于预测与样本点不重合的其他数据点，则采用PLS部件重构方法，计算精度比传统方法和BP神经网络的高，稳定性比BP神经网络的好。

（3）对于压气机来说，采用2元偏最小二乘法还是3元进行特性重构，要具体问题具体分析，主要受部件特性线形状、样本数量等的影响。对于本文分析的情况，建议使用2元偏最小二乘法。

[1]Changduk K，Seonghee K，Jayoung K.Component map generation of a gas turbine using genetic algorithms[J].Journal of Engineering for Gas Turbines and Power，2006，128（1）：92-96.

[2]尹大伟，李本威，王永华.基于Kriging方法的航空发动机压气机特性元建模[J].航空学报，2011，32（1）：99-106. YINDawei，LIBenwei，WANGYonghua.Aeroenginecompressor characteristics metamodeling using Kriging method [J]. Acta Aeronautica etAstronautica Sinica，2011，32 （1）：99-106.（in Chinese）

[3]崔茂佩.压缩机特性线的系数拟合法 [J].热能动力工程，1999（1）：43-46. CUI Maopei.A coefficient fitting method for compressor characteristic curves[J].Journal of Engineering for Thermal Energy and Power，1999（1）：43-46.（in Chinese）

[4]王志涛，李淑英，谭智勇.基于BP和RBF神经网络压气机特性曲线拟合方法的研究[J].汽轮机技术，2009，51（2）：94-96. WANG Zhitao，LI Shuying，TAN Zhiyong.Comparing study on the fitting method of compressor characteristic curve based on BP and RBF neural network [J].Turbine Technology，2009，51（2）：94-96.（in Chinese）

[5]MaciejL.Jetengine turbine and compressor characteristics approximation by means of artificial neural networks[C]//Adaptive and Natural Computing Algorithms.Warsaw：8th International Conference. ICANNGA 2007：143-152.

[6]Gholamrezaei M，Ghorbanian K.Compressor map generation using a feed-forward neural network and rig data：Part A [J].Proceedings of the Institution of Mechanical EngineersJournal of Power and Energy，2010，224（1）：97-108.

[7]Ghorbanian K，Gholamrezaei M.An artificial neural network approach to compressor performance prediction[J].Applied Energy，2009，86（7-8）：1210-1221.

[8]段绍栋，肖玲斐，申涛.基于功率反馈的涡轴发动机神经网络PID控制研究[J].航空发动机，2012，38（2）：11-14. DUAN Shaodong，XIAO Lingfei，SHEN Tao.Neural networks PID control of turboshaft engine based on power feedback[J].Aeroengine，2012，38（2）：11-14.（in Chinese）

[9]雷积红，陈策，李军，等.基于BP神经网络的涡扇发动机部件特性研究[J].燃气涡轮试验与研究，2003，16（4）：15-17. LEI Jihong，CHEN Ce，LI Jun，et al.A study of turbofan component characteristic based on back-propagation network [J].Gas Turbine Experiment and Research，2003，16（4）：15-17.

[10]王惠文.偏最小二乘法及其应用 [M].北京：国防工业出版社，1999：150-171. WANG Huiwen.Partialleastsquaresregression method and applications[M].Beijing：National Defence Industry Press，1999：150-171.（in Chinese）

[11]Svante W，Paul G，Kim E，et al.Multi way principal components and PLS analysis[J].Journal of Chemometrics，1987，1（1）：41-56.

[12]Svante W，Michael S，Lennart Er.PLS-regression：a basic tool of chemometrics[J].Chemometrics and Intelligent Laboratory Systems，2001，58（1）：109-130.

[13]马文通，苏明，余南华.变几何多级轴流式压气机特性估算[J].中国电机工程学报，2008，28（11）：72-76. MA Wentong，SU Ming，YU Nanhua.Characteristic estimation method of variable geometry multistage axial-flow compressors[J].Proceedings of the Chinese Society for Electrical Engineering，2008，28（11）：72-76.（in Chinese）

[14]马文通，刘永文，苏明.基于平均微元级特性的压气机特性线外推方法[J].动力工程学报，2007，27（3）：323-326. MA Wentong，LIU Yongwen，SU Ming.Extrapolation of performance curves ofcompressors based on averaged infinitesimalstage characteristics [J].Journal of PowerEngineering，2007，27（3）：323-326.（in Chinese）

[15]曾进，任庆生，翁史烈，等.基于神经网络的燃气轮机动态过程仿真[J].热能动力工程，2000，15（4）：423-425. ZENG Jin，REN Qingsheng，WENG Shilie，et al.Simulation of a gas turbine dynamic process on the basis of a neural network[J].Journal of Engineering for Thermal Energy and Power，2000，15（4）：423-425.（in Chinese）

[16]Robbins W H，Dugan J F.Prediction of off-design performance of multi-stage compressors [M].Washington：NASA SP-36，1965：297-310.

（编辑：赵明菁）

Accuracy Research on Processing Methods of Component Characteristics in Gas Turbine Simulation

SUN Bo1，PENG Shu-hong1，WU Ke-liang1
（Shanghai Electric Gas Turbine Co.，Ltd.，Shanghai 200240，China）

In the gas turbine performance simulation process based on component characteristics,the accuracy description of component characteristics curve affect the simulation results significantly.Different component characteristics curve methods including traditional modeling method,neural network method and PLS （partial least square）method were introduced.An actual gas turbine was taken as an example,and the effect on performance simulation accuracy of components and entire machine using different characteristic processing methods was analyzed based on part of given performance data.The results were compared with the other part of the given performance data.Results show that PLS method can be used in refactoring equation directly in the simulation process,it could avoid the interpolation errors of component characteristics compared with traditional processing methods,improve the accuracy of the gas turbine thermodynamic model.

gas turbine;performance simulation;characteristic curve;modeling;processing method

V 231.1

A

10.13477/j.cnki.aeroengine.2015.05.009

2015-05-27

孙博（1982），女，博士，从事燃气轮机性能仿真，控制策略分析及二次空气系统计算分析等工作；E-mail：sunbo@shanghai-electric.com。

孙博，彭淑宏，吴克梁.燃气轮机仿真中部件特性处理方法的准确性研究 [J].航空发动机，2015，41（5）：43-48.SUN Bo，PENG Shuhong，WU Keliang.Accuracy research on processingmethods ofcomponents characteristics curve in gas turbine simulation [J].Aeroengine，2015，41（5）：43- 48.