基于粗糙集的BP神经网络空气品质预测模型

徐凌雁

(中国电信吉林市分公司，吉林吉林132012)

近几十年以来，由于世界各国工业的高速发展以及人口的急剧扩张导致世界范围内能源需求与交通规模的持续扩大，世界人口的急剧膨胀也使得人们各类生产和生活中所产生大量的有害物质被排放到大气中从而改变了空气的组成成分最终形成“空气污染”［1］。空气污染是世界大多数工业化国家所面临的极为严重的环境问题。随着人们对城市空气质量的关注逐渐提高，民众希望能够得到城市环境空气质量的监测结果，以使广大民众及城市环保部门对城市环境空气质量的情况做到如天气预报一样可以提前预知，便于对即将出现的城市空气问题采取及时有效的风险预控措施。利用基于人工神经网络的模式识别法来进行空气品质预测，可以不需要使用白盒的方法来确定显式模型而是根据输入的监测数据来创建黑盒模型。依靠模式识别方法的非线性问题处理能力和噪声冗余能力，可以基于不同地区空气品质系统的实际工况，构建属于特定地区空气品质特点的人工神经网络预测模型［2］。

1 基于粗糙集的BP神经网络

1.1 BP结构

倒传递类神经网络是将输出层的误差，逐层往输入层倒向传递分配给各层，以提供各层的误差参考，进而改善相应的连结权值，并调整实际输出值与期望输出值间的误差。

1.1.1 BP算法

倒传递学习算法是广泛使用的监督式学习模式。倒传递学习算法可分为向前馈入和误差向后推导，而这两部分皆需由迭代演算处理［3］。向前馈入步骤是将欲学习数据由输入层输入，再向前传至第一隐藏层，经隐藏层节点的转换函数处理后，得到相对应的输出值，此输出值又向前传至第二隐藏层，变成第二隐藏层的输入值;如此逐层的向前传送，最后由输出层输出结果。接着比较向前馈入步骤中的实际输出值与期望输出值。若误差符合系统要求，则学习宣告结束，并将各连结上的权值当成是训练后的知识;相反的，若是误差超过系统要求，则进行误差向后推导的步骤。此时，误差将由输出层向后逐层的往输出层传递，并修改各层连结上的权值，经反复迭代运算达到系统误差要求为止。

1.1.2 BP神经网络的缺点

BP神经网络算法的提出，有效的解决了针对非线性连续函数求解多层前馈神经网络的权值的难题。此外，BP神经网络给出了完整的数学公式推导。由于BP神经网络在数学上的完整性使其广泛地应用于多种领域。

尽管如此，BP神经网络算法也存在一些缺点，主要表现在:

(1)无法确定BP神经网络的泛化能力;

(2)BP神经网络在误差梯度平摊处收敛缓慢;

(3)BP神经网络在训练过程中可能陷入局部极值点;

(4)学习算法的收敛速度慢。

1.2 粗糙集理论

在本世纪70年代，波兰学者Z.Paw lak和一些波兰科学院、波兰华沙大学的逻辑学家们，一起从事关于信息系统逻辑特性的研究。粗糙集理论就是在这些研究的基础上产生的。1982年Z.Paw lak发表了经典论文Rough Set s，宣告了粗糙集理论的诞生。此后，粗糙集理论引起了许多数学家、逻辑学家和计算机研究人员的兴趣，他们在粗糙集的理论和应用方面作了大量的研究工作。目前，粗糙集已成为人工智能领域中一个较新的学术热点，在机器学习、知识获取、决策分析、过程控制等许多领域得到了广泛的应用［4，5，6］。

基于粗糙集的数据分析方法实际是对决策表进行约简的过程，这个处理过程具体如下:首先把智能数据进行离散归一化处理，即把连续的数据进行离散化整理，变换成若干个属性值，这样的处理既满足属性值尽量少，又满足离散化的信息丢失尽量少;然后将数据用知识表达属性表的表格来实现;删除决策表中重复的实例，即消去重复的行，重复的行表示同样的决策，因此被消去;删除多余的属性，即从知识表达属性值表中消去某些列;删除每个实例中多余的属性值，求出最小约简;由最小约简求出逻辑规则，即最小控制决策算法。

本文采用粗糙集方法对济南市环境空气质量与污染源数据库中的数据进行数值离散化、字段筛选等操作，以实现属性约简，并抽取精简规则，以简化神经网络的拓扑结构，提高训练样本的质量，缩短训练时间。

1.3 算法结构

基于BP神经网络算法的模型结构与特点，可使该算法应用于空气污染物浓度分析预测。空气污染监测的主要污染物是空气中二氧化硫(SO2)、可吸入颗粒物(PM10)与二氧化氮(NO2)的含量。选择与污染物扩散有关的主要气象数据即风向、风速、气压、湿度、温度作为特征参数。通过使用气象参数对选择特定气象条件的污染物排放时间段对空气品质监测站中采集到的各时段数据进行粗糙集属性约简，然后进行特征提取。根据这些规则构造BP神经网络算法中隐含层神经元的个数，然后定义对应节点间的权值连接，故而确定了BP神经网络算法的初始结构。将空气品质监测站采集到的数据作为BP神经网络的训练样本，将选定区域污染源排放的相关数据作为输入量，空气品质监测站的污染物浓度数据作为输出量，对三种不同的污染物、不同的气象参数形成多个训练样本并进行算法迭代训练，求出BP神经网络的各种相关参数，建立对应不同污染物的空气品质预测网络模型，BP神经网络模型如图1所示。

图1中，第1层为神经网络的数据输入层，输入层的数据是监测站实际测量到的污染物浓度，表示为输入矢量x=(X1，X2，，，Xn)T″，在本文中为经过数据归一化处理后所得到的污染源的污染物实际排放出的数据，用粗糙集理论的属性约简中的算法对输入层的数据进行属性约简，由于监测的污染源为25种，污染物检测站总共为8个，得到空气品质监测系统的属性是25个，因此空气品质监测系统输入层的节点数为25。

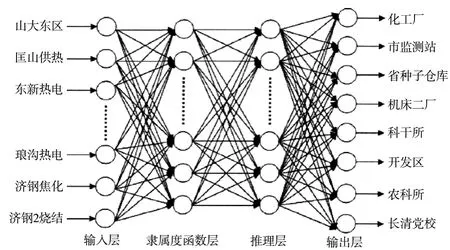
图1 BP神经网络模型

第2层为隶属度函数层，该层分别将输入层中的n个输入分量(Xl，X2，…，Xn)中的每一个输入分量依照某种不可分辨关系离散化处理得到ri个不同的数值，这些数值在［0，1］之间，空气品质监测系统的节点数为5。

使用Gauss函数作为该层神经元的作用函数:

其中i=1，2，…，n;j=l，2…，ri;n=25。

第3层为推理层，推理层中的每个节点分别对应一条规则。这些规则是通过上述的粗糙集约简后所得到的，所以空气品质监测系统中推理层的节点数也就是规则数是5。

假设有k(k＜n)条规则，推理层节点的作用函数为公式(2):

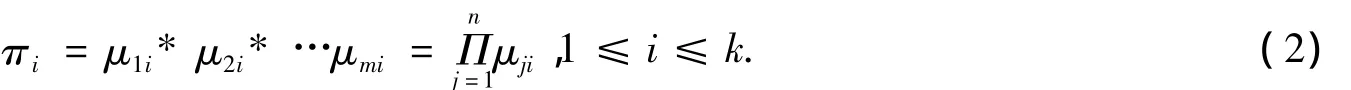
第4层为输出层，输出层的节点表示输出变量，在本文中为经过离散化处理的空气品质监测站的监测数据。由于监测的污染物为25种，污染物检测站总共为8个，所以空气品质监测系统输出层的节点数为8，空气品质监测系统输出层权值的初始值wij(1＜j＜8)是预先设定在推理层中各规则的置信度值，所以空气品质监测系统输出层节点的值为:

1.4 BP预测模型的训练

根据上述空气品质预测模型，BP神经网络的输入层有25个节点，第二层隶属度函数层有5个节点、第三层推理层有5个节点数、第四层输出层有8个节点。此外空气品质监测系统中第三层推理层与其第四层输出层之间的连接权值用选取的各规则的置信度作为初选值，经计算可知其初选值为{0.82，0.94，0.92，0.89，0.87}，BP神经网络其他层的参数取［0，1］之间的随机数作为空气品质监测系统的初选值。空气品质监测系统中误差初始值将直接影响BP神经网络模型的训练时间以及输出的精确性，因此本文选取误差范围取i=0.000 001，学习速率为0.5。

根据不同的气象环境参数与针对监测不同污染物浓度而构建的BP神经网络模型，在空气品质监测数据库中选择针对不同气象参数的空气污染物排放源的污染物排放量和空气品质监测站的污染物浓度监测值作为神经网络的训练样本。选择好训练样本后，将每一条样本数据输入空气品质监测模型进行计算。如果模型的输出值与设定值之间的误差小于误差参数E，则停止本条样本数据的计算，并将下一条样本数据输入模型进行训练;如果输出值与设定值的偏差大于E，就需要调整模型的中间参数权值，并对该条样本数据重新进行计算，直到输出值与设定值的偏差小于E为止。通过上述方法训练后，空气品质监测模型的各项权值参数全部调整完成。

根据需要预报污染物浓度所在地区的气象参数，选择相同时间段，相同气象参数的空气品质监测站的监测数据作为监测模型的输入数据，并对该数据进行归一化处理。输入具有相同气象参数的已经调整好各项参数的空气品质预测模型进行计算。将计算后的输出数据经过归一化算法反推出的数据就是这种污染物在该气象参数条件下的污染物浓度预测值。

2 数据分析

2.1 样本数据

取2013年5月18日，下午15时的数据，下午15时的气象参数是:风向西南风，风速为1.2 m/s，温度是15℃，相对湿度是25%(用气象局中的数据)，气压是820百帕。则25个监测污染物排放源的NO排放浓度(单位:kg/h)如表1所示。

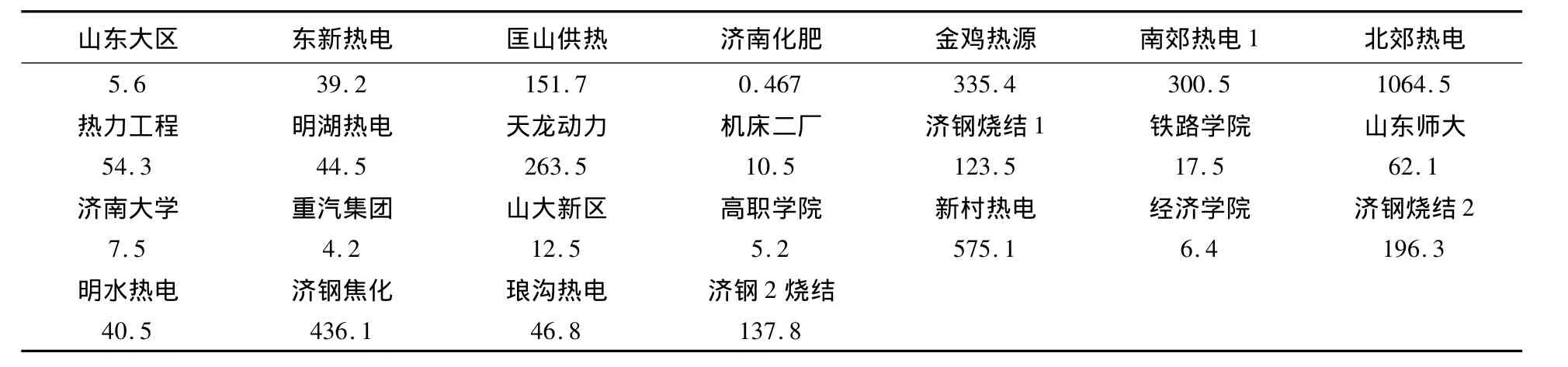
表1 2013年5月18日15时NO排放量(单位:kg/h)

对输入的数据进行参数归一化算法处理，为便于模型处理，将各污染物的排放源的数据除10 000，使得它们归入O和1之间，得到如表2所示的数据。

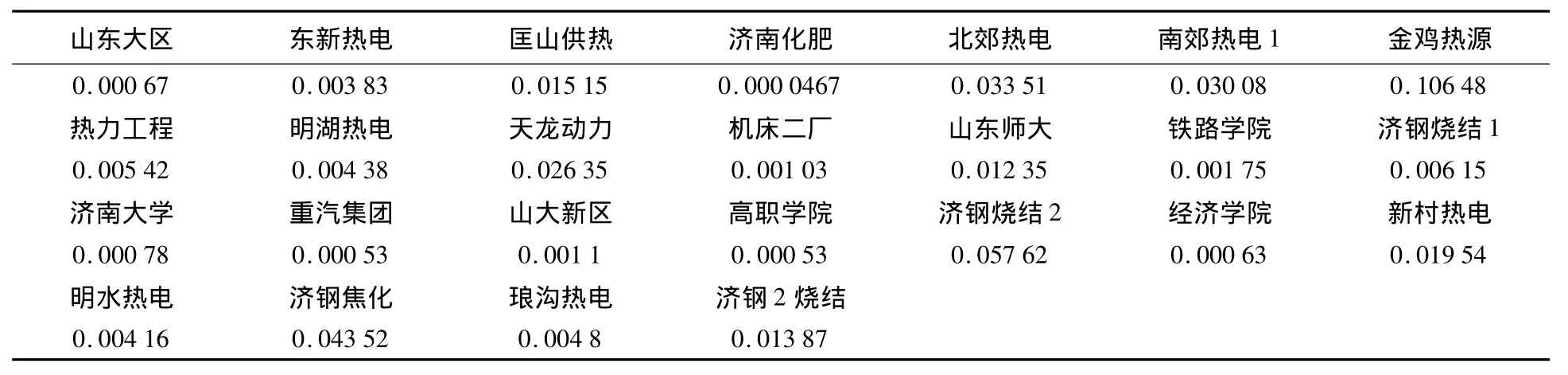
表2 归一化的污染源NO排放数据

8个空气品质监测站的NO监测浓度(单位:mg/tns)，如表3所示。

表3 2013年5月18日下午15时的空气品质监测值(单位:mg/tns)

2.2 网络初始化

中间隐层数为2，隶属度函数层和推理层的单元数均为5。初始化网络权值，输入层与隶属度函数层之间的连接权值为W12。

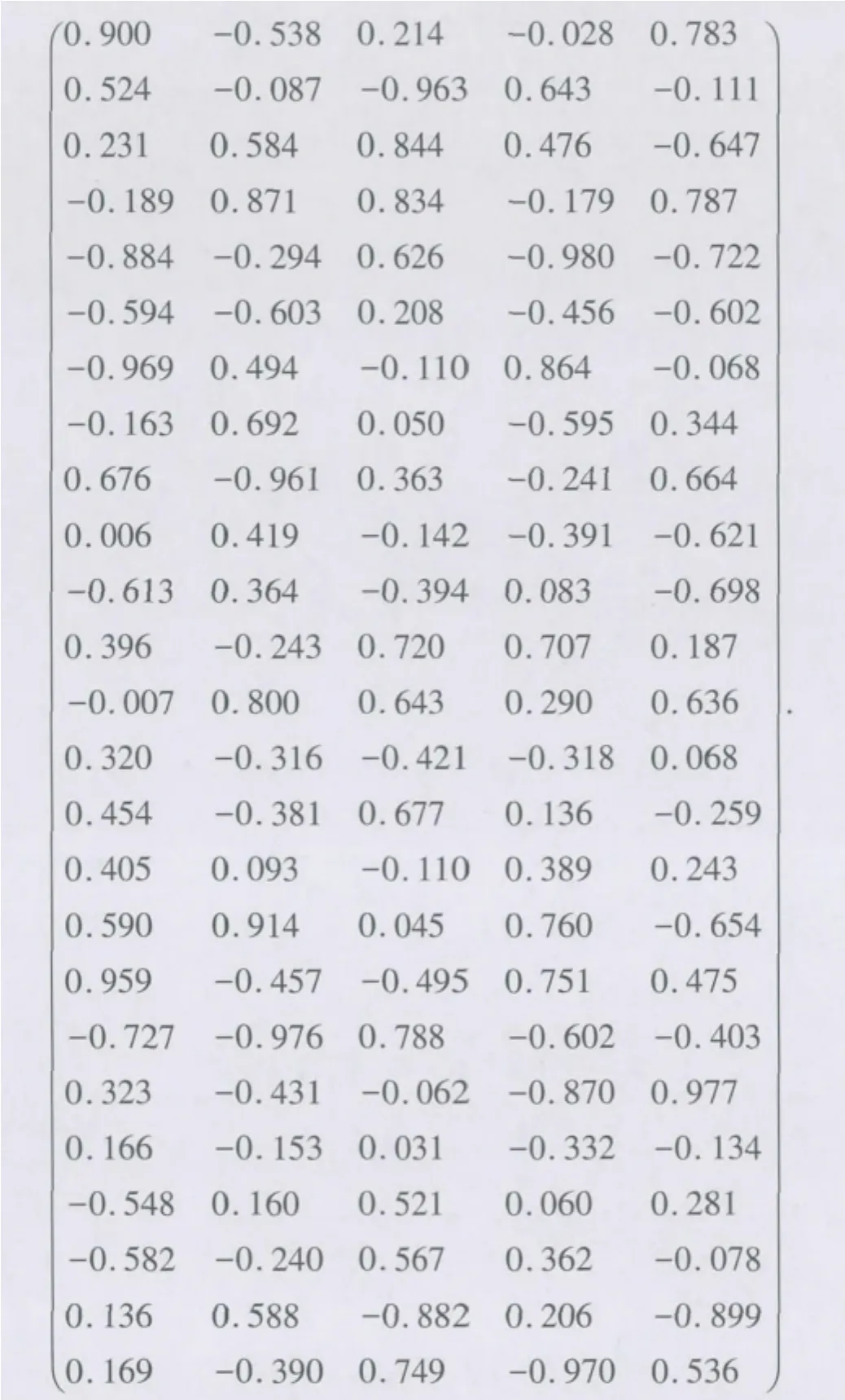
第二层隶属度函数层与第三层推理层之间的连接权值为W23

第三层推理层与空气品质监测系统第四层输出层的连接权值W34为空气品质监测系统中BP算法各规则的置信度，即为

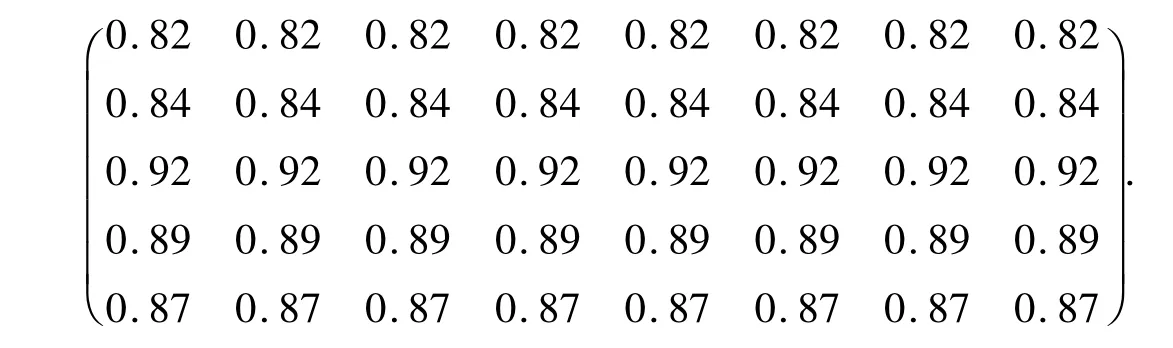
对系统的第2、3、4层的节点阈值进行初始化，阈值如表4所示。

表4 BP算法第2、3、4层节点阈值θ

2.2 污染物浓度预测

选择2013年6月26日下午15时污染物排放源数据进行污染物浓度预测，当时的气象条件是:风向是西南风，风速是1.3 m/s，温度是19℃，湿度是25%，气压是825 Pa和用于神经网络训练所使用的2013年5月18日，下午15时的气象条件基本相似。污染物NO排放数据如表5所示。

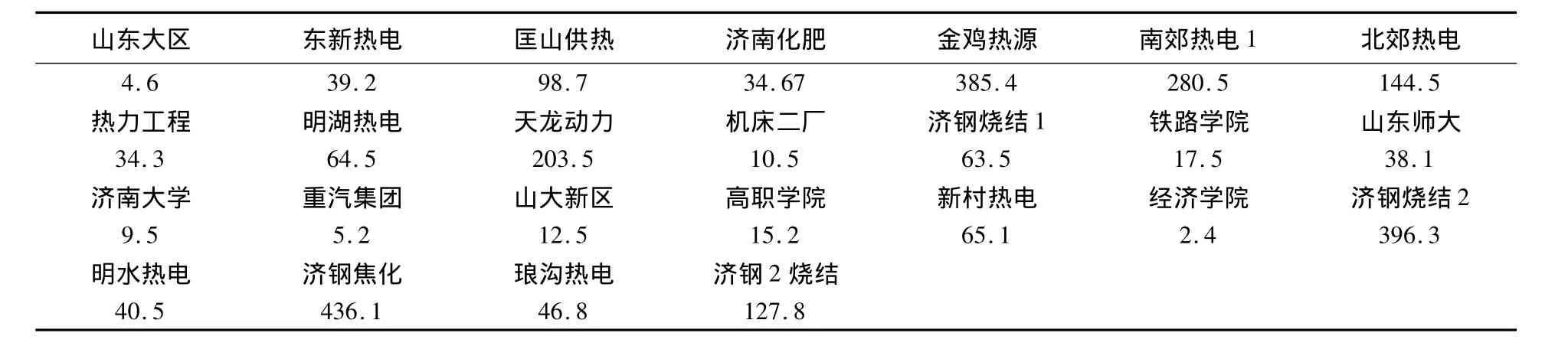
表5 2013年6月26日15时污染源NO排放数据(单位:kg/h)

2.3 两种预测模型的预测结果比较

用基于粗糙集的BP神经网络污染物浓度预测模型与一般神经网络的空气品质预测模型分别进行污染物浓度预侧，得到的结果如表6所示。

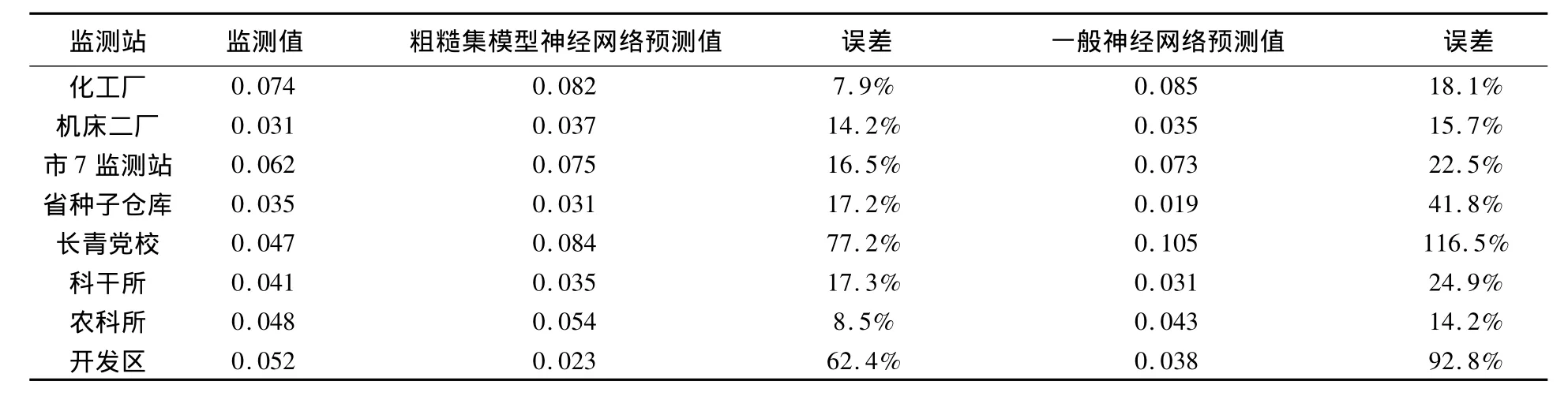
表6 两种空气品质预测模型比较结果

从表6中可以看出基于粗糙集的空气品质预测模型比一般的BP神经网络的空气品质预测模型在污染物浓度预测准确性方面具有一定的优势。因为基于粗糙集的空气品质预测模型的中间隐层数为2，隐层节点的数目由粗糙集抽取出的满足最小置信度条件的规则的条数决定;但是普通的BP神经网络空气品质预测模型的中间隐层数为1，此外BP神经网络的隐层节点数由人为指定的，主要依靠经验值并没有没有科学依据。

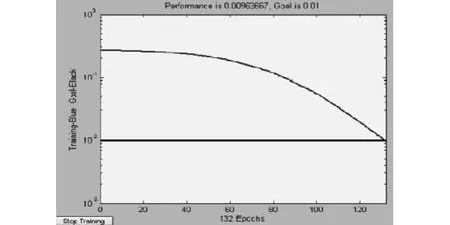
图2 基于粗糙集的BP算法误差变化曲线

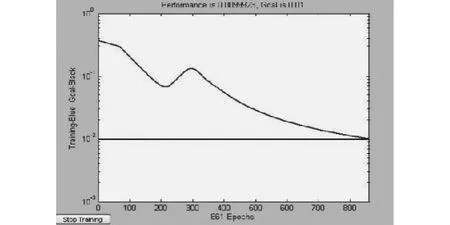
图3 基于BP算法误差变化曲线

对图2与图3进行比较明显可以看出，实现同样训练目标误差精度时，BP算法需要861步训练后网络性能达到要求，基于粗糙集的BP算法仅需要132步训练后网络性能达到要求。由此可见，采用粗糙集BP算法训练网络提高了网络收敛的速度，具有较好的自适应性。

4 结论

综上所述，利用基于人工神经网络的模式识别方法来进行环境空气品质预测模型的研究并将空气品质监测站获得的海量空气污染物浓度数据的可视化分析以及研究区域空气品质与区域空气品质监测数据的相关性对于定量分析特定区域范围内的环境空气品质状况、污染物的扩散情况有着重要的作用。这不仅在论证人们的生产活动和生活活动对地球环境空气品质产生何种影响这个哲学问题上有着重要理论意义，而且对区域的环保管控、污染物控制、城市规划、环保规划、交通建设此外公共卫生都具有十分重要的实际价值。

［1］唐易达，肖德玲，王会燃.室内空气品质的远程监测与评价［J］.仪器仪表与分析监测，2005，20(1):12－13.

［2］刘建龙，张国强，郝俊红，等.便携式CO2红外分析器检测室内环境时的使用方法［J］.分析仪器，2004，17(2):56.

［3］武尚，程红福，明晓乐.基于优势关系的粗糙集扩展研究［J］.计算机与数字工程，2014，8(6):943－947.

［4］孙文兵，曾祥燕，杨立君.BP网络和多元回归在葡萄酒质量模型中的应用［J］.计算机工程与应用，2014，3(15):267－270.

［5］刘丽丹，温静雅，刘建华.校园空气质量监测与综合评价［J］.东北电力大学学报，2013，33(4):43－47.

［6］邓冠男.聚类分析中的相似度研究［J］.东北电力大学学报，2013，33(1):156－161.