基于DEA的全国电网供热效率综合评判模型的研究

曲如，楚帅

(东北电力大学理学院，吉林吉林132012)

电网规划综合评判决策［1－4］影响因素较多且复杂，由于城市高压配电网规模很大，在电网规划综合评判时，决策者需要考虑电网的技术性、经济性以及对社会未来的适应性等多种评价指标。数据包络分析法可以很好的综合各种因素，对城市高压配电网进行评判。

从目前的实际应用看，国内使用较多的两个模型是C2R模型和BC2模型，其中，C2R模型可以用来评价决策单元是否同时达到规模有效和技术有效，BC2模型则可以用来评价决策单元的技术有效性。而城市配电网的发电量规模受城市用电量影响，所以我们不需要考虑其规模有效性。因此，利用BC2模型就可以对各城市配电网进行评判。

传统的BC2模型无法对各个有效的决策单元进行排序，为了得到最优的效率值，我们在计算时，引入改进后的DEA交叉效率模型［5，6］。经实例验证，结果可信、客观合理。

1 BC2模型

BC2模型是评价决策单元技术有效性的一个重要模型，在整个DEA理论体系中具有重要地位。BC2模型不考虑生产可能集满足的锥性，其规划模型(DBC2)为:其中:xij和yrj分别为第j个决策单元对第i种输入的投入量和对第r种输出的产出量，xij＞0，yrj＞0;其中，i=1，2，…，m;r=1，2，…，s;j=1，2，…，n。为方便起见，记xj=(x1j，x2j，…，xmj)T，yj=(y1j，y2j，…，ysj)T，j=1，2，…，n。

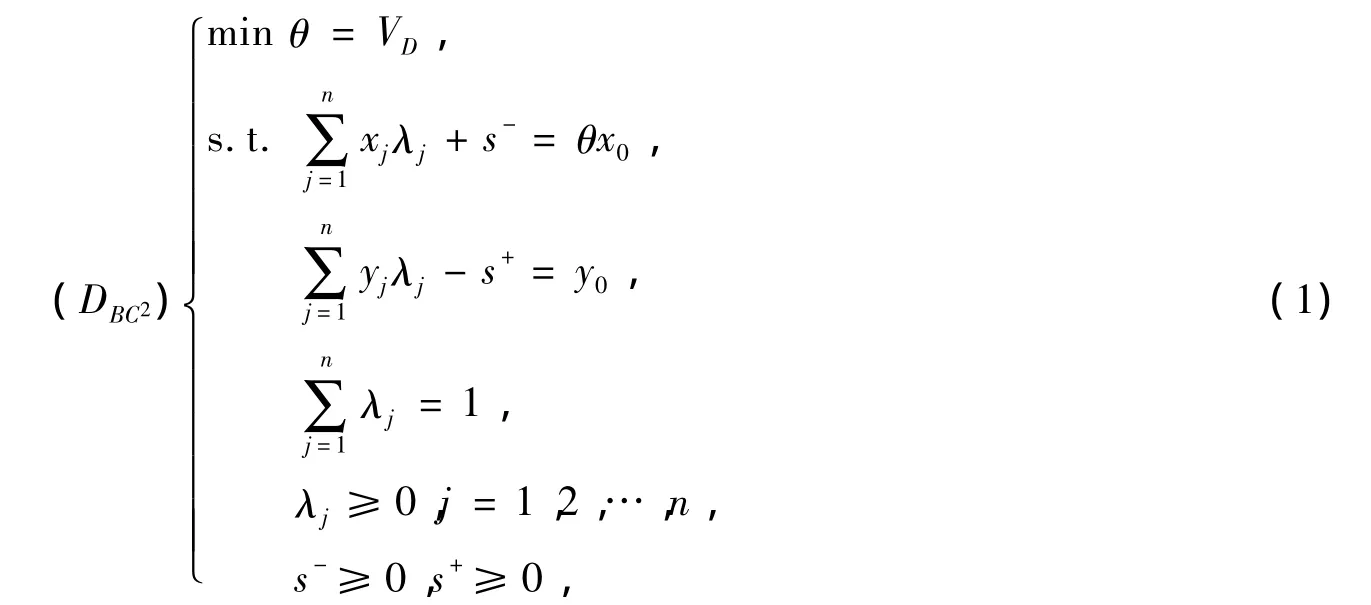
对于线性规划(DBC2)的任意最优解λ0，s－0，s+0，θ0都有:

(1)若θ0=1，则决策单元j0为弱DEA有效(BC2);

(2)若θ0=1，并且s－0=0，s+0=0，则决策单元j0为DEA有效(BC2)。

2 BC2模型的改进

2.1 基于BC2的交叉效率模型

在实际计算时，可能遇到多个决策单元的效率值都是1，这是因为传统的BC2模型无法对各个有效决策单元进行排序，为了得到最优的效率值，我们在计算时引入改进后的交叉效率模型，该模型的表达式如下

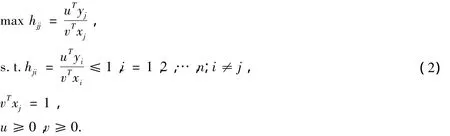
模型(2)的对偶模型如下:

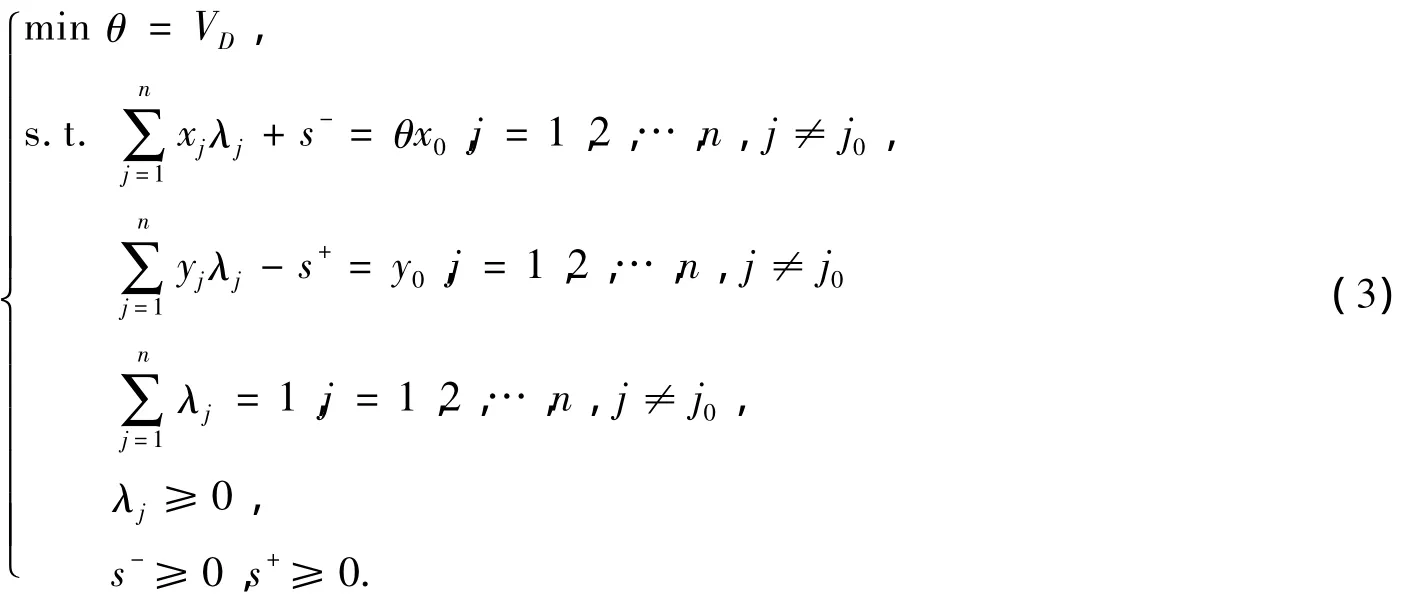
改进后的模型的主要改进点在于评价第j0个单元时，使该决策单元与其他所有的决策单元的线性组合做比较，让第j0个决策单元的产出和投入被其他所有的决策单元的产出与投入的线性组合替代，即将第j0个决策单元排除在外。因为没有了hjj≤1的约束，所以对于DEA有效的单元效率评价值可大于1。这样会使交叉效率评价结果更加客观、合理。

2.2 BC2模型改进后的交叉效率矩阵

由模型(2)可以得到，对于每一个决策单元DMUj都有相应的效率评价指数

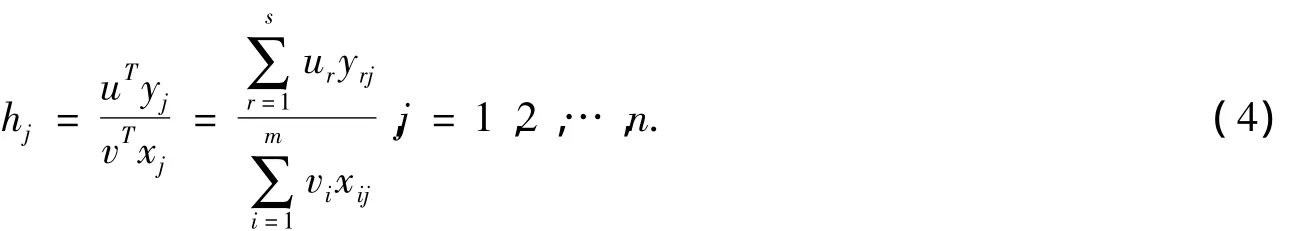
基于BC2改进后的模型，本文定义交叉效率矩阵

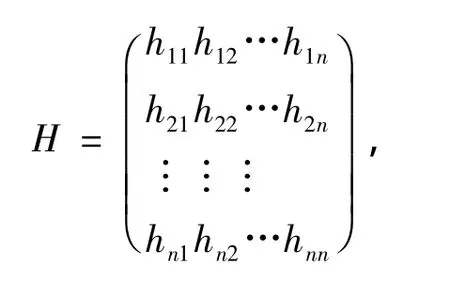
其中:主对角元素hjj(j=1，2，…，n)为自我评价值;非主对角元素hji(j≠i)为交叉评价值。

对于每个DMUj，通过求解模型(2)确定输入与输出权重向量，当得到最优权重和后是DMUj自我评价数值，进一步可计算出其他单元的交叉评价值hji(j≠i)，即可计算得到交叉效率矩阵H。

3 基于DEA的交叉效率模型的应用

电网规划涉及了多方面影响因素，不但包括配电网赖以生存的社会经济环境、配电网服务对象、自身的经济技术条件，而且还包括配电网发展趋势等因素。因此，评价指标选取的优劣直接影响了电网规划的科学合理性。本文建立评价指标的层次结构(详见图1)，确定技术经济评价的核心指标，在充分考虑供电方和用户的利益基础上，最终通过此评价方法使经济效益和社会效益总体达到最优。

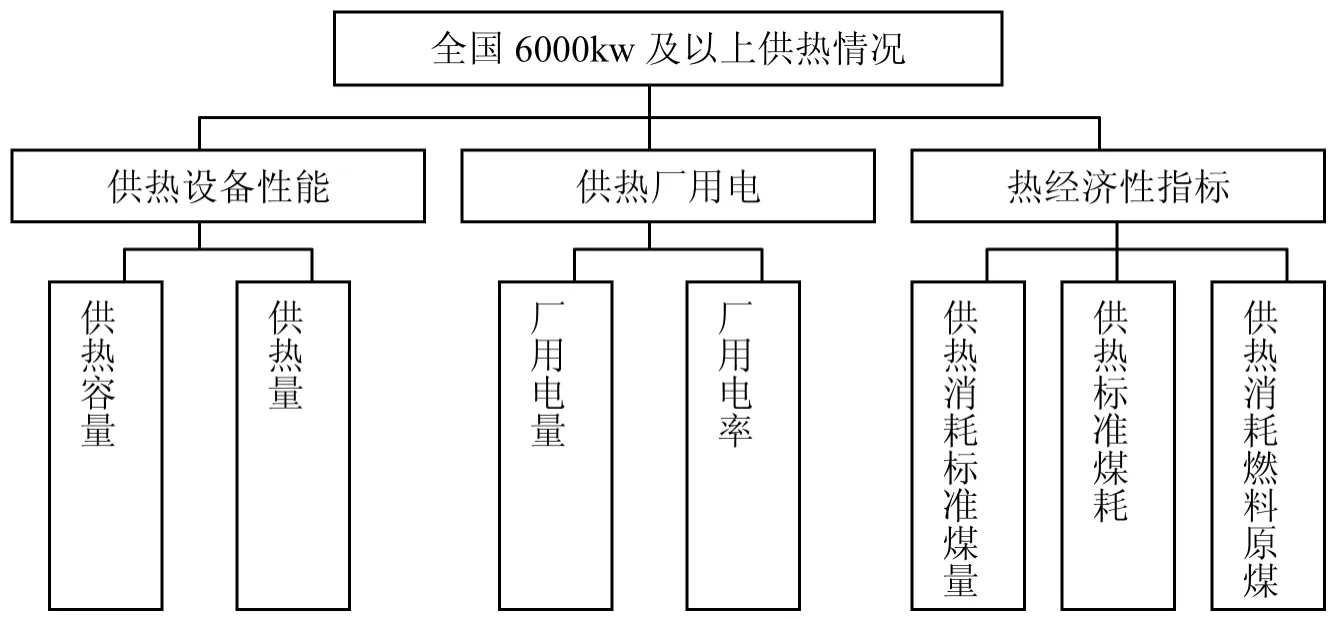
图1 电网供热效率评价指标集

4 实例分析

为了验证本文方法的科学有效性，采用文献［7］中的2013年中国电力年鉴中电力行业统计资料，按照本文建立起来的评价体系流程进行计算。

算例概述:通过对全国各城市6 000 kW及以上的电厂供热情况进行评判，然后对全国各城市的供热效率进行排序。

确定输入和输出指标。结合电网规划实际情况，依据最原始经典BC2模型的选择条件，本文选取“越小越好”的评价指标作为该模型的输入量，选取“越大越好”的评价指标作为模型的输出量，输入指标有供热厂用电量、供热厂用电率、供热消耗标准煤量、供热标准煤耗、供热消耗燃料原煤;输出指标有供热容量、供热量。

表1是运行未经改进的BC2模型得到的效率值，可以观察到，有12个城市的效率值为1，因此，运用传统的BC2模型无法对这12个城市进行排序。表2是对上述12个城市，应用改进后的交叉效率模型得到的结果。可以看出，各决策单元的效率值均大于1，并且各不相同，从而可以对决策单元的技术有效性进行排序，排序结果见表3。

在表3的计算结果中，我们可以清晰的观察到全国各城市的发电供热效率(即燃煤利用率)排名。从经济发达的角度来看，全国的一线城市排名较为靠前，其发电供热率较高，例如北京、上海、广东等，这说明经济相对发达的城市，在发电供热时资源投入这方面做的也很好。从地域划分来看，北方地区的发电供热效率则相对较高，例如山西、内蒙古等地区，其排名非常靠前。

5 结论

(1)本文将基于DEA的交叉效率评价模型应用在全国电网发电效率的综合评判决策中，建立了一套完整的电网发电效率评价决策的综合评价指标体系，计算过程清晰、简便，结果科学可信，具有较大的推广性。

(2)本文提出的方法较DEA模型的效率值大小分布更加合理，降低了DEA模型评价值的极端与不合理情形，切实客观地体现了决策单元实际效率状况。

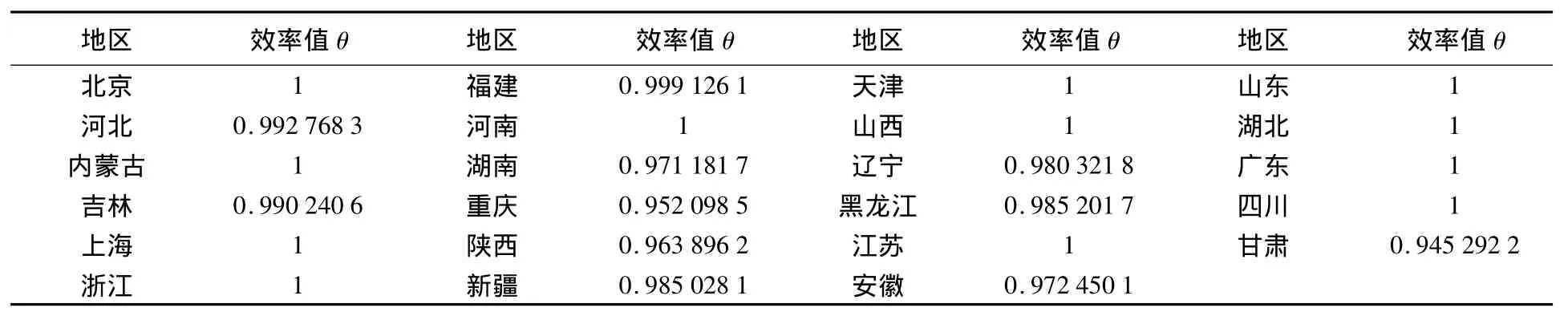
表1 各决策单元在BC2下的效率值

表2 各决策单元在改进后的交叉矩阵下的效率值

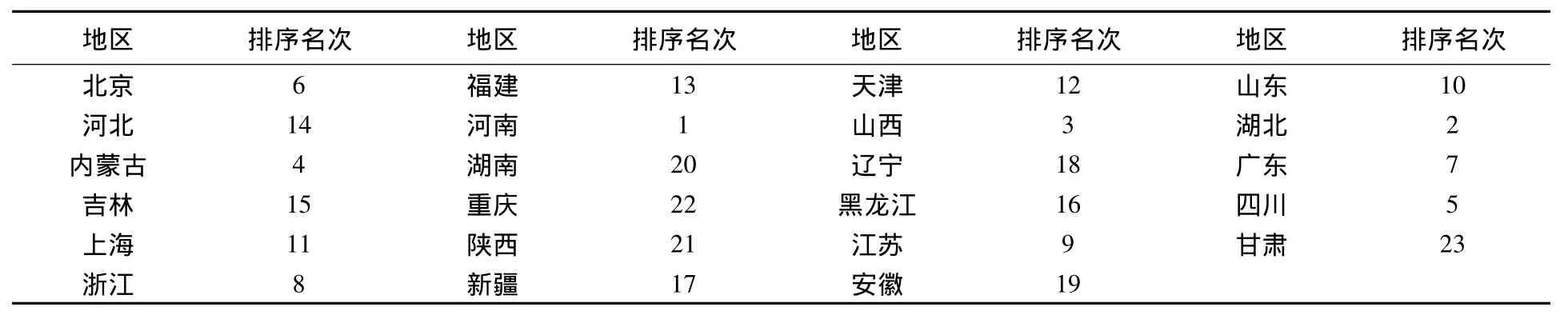
表3 各城市的排序结果

［1］Sheehan M，Willeams S H.Optimal allocation of resources to distribution investments using the analytic hierarchy process to balance the impacts of investments on safety，customer interruption costs，levelized annual revenue requirement contribution to margin and other considerations［C］.Power Engineering Society Summer Meeting，IEEE，2000，3:1311－1316.

［2］刘佳，韦钢，吴伟力.应用PCA－C2R模型综合评判电网规划方案［J］.电力系统保护与控制，2008，36(20):20－24.

［3］韦钢，吴伟力，刘佳等.基于SE－DEA模型的电网规划方案综合决策体系［J］.电网技术，2007，31(24):12－27.

［4］万国成，吴日升，樊亚亮.城市电网规划建设与城市规划的关系探讨［J］.广东电力，2006，19(5):28－31.

［5］曲如，李晗，刘悦.基于DEA方法的学生有效努力程度的评价研究［J］.东北电力大学学报，2013，33(6):1－4.

［6］王香柯，王金柱.基于数据包络分析模型的学习效率评价研究［J］.东北电力大学学报，2002，18(1):66－68.

［7］魏昭峰.中国电力年鉴2013［Z］.中国电力，2013:619－624.