真域贴近模糊推理算法

邓冠男，宋莲莲

(东北电力大学理学院，吉林吉林132012)

模糊推理是进行模糊信息处理和实现机器智能的重要工具，也是模糊控制器的核心［1，2］。给定一组模糊规则:

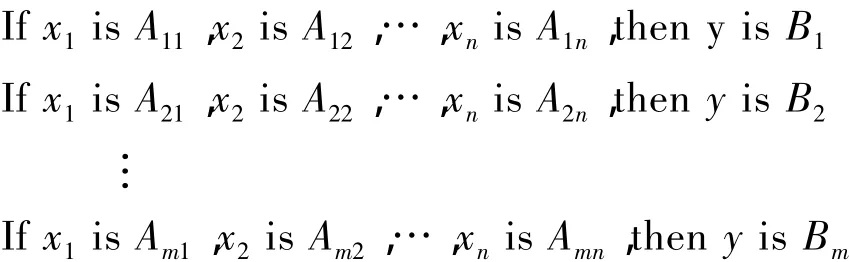
以及某一事实x1is，x2is，…，xnis，模糊推理的基本问题是根据给定模糊规则，按照给定事实，确定能够得到怎样的推理结果y，这里Aij和(i=1…m，j=1…n)是论域Xj上的模糊集，Bi是论域Y上的模糊集。这样的模糊推理问题以简单的FMP(Fuzzy Modus Ponens)模型为基础，即给定规则If x is A，then y is B及事实x is A*，求推理结果y。

为解决模糊推理问题，1973年，Zadeh［3］首先给出模糊推理理论中最基本的规则即模糊分离规则，随后Mamdani等人［4］又将其算法化，形成如今广泛使用的CRI方法(Compositional Rule of Inference)。CRI方法首先利用蕴涵算子将模糊规则A→B转化成一个X×Y上的模糊关系R，然后将A*与R进行复合即得到B*:

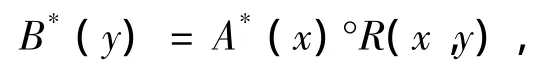
其中，R通常称作A→B的真域。CRI方法由于其简单易用的特点，自从其产生以来，逐渐成为广泛使用的一种模糊推理算法。然而，模糊推理远较经典逻辑学中的二值推理复杂得多，李洪兴［5］指出基于CRI方法的模糊系统本质上是一种插值器。王国俊［6］指出CRI方法在求B*时采用了复合运算，这一步带有一定的随意性，偏离了语义蕴涵的框架。

为了解决CRI方法的不足，许多学者提出了多种模糊推理算法，如真值推理法［7］、全蕴涵三I算法［6］、基于相似度的模糊推理算法［8，9］、真值流推理法［10］、变权综合模糊推理［11］、简易插值模糊推理［12］、SIS算法［13］、基于神经网络的模糊推理［14］、最优模糊推理方法［15］等等，更多的可见参见文献［16］。然而，尽管模糊推理的算法有很多，但是这方面的研究大多停留在理论层面，在实际中很少有成功的运用，并且由于推理结果缺乏评价机制，因此无法直接衡量各个算法的优略。

近来，我们在文献［17］中提出一种新的模糊推理算法，称之为真域贴近模糊推理算法，其基本思想是通过最大化A→B的真域与A*→B*的真域之间的贴近度来获得推理结果。本文中，我们将进一步对这种算法进行研究，探讨真域贴近模糊推理算法与CRI方法的联系，研究采用最大－最小贴近度及某些常用蕴涵算子的真域贴近模糊推理算法，比较真域贴近模糊推理算法与CRI方法及全蕴涵三I算法的推理能力。

1 真域贴近模糊推理算法的基本原则

真域贴近模糊推理算法基于模糊推理的一种假设，即在FMP问题中，当给定事实A*与规则前件A偏离不大时，推理结果B*与规则后件B偏离也不大。因而，为了保持原有推理规则的正确性，应该使A*→B*的真域R*尽可能地接近A→B的真域R。在模糊集理论中，通常采用贴近度来度量模糊集之间的接近程度，因此若设δ为一个贴近度函数，则真域贴近模糊推理可以描述为一个优化问题，即

一般来说，(1)式的求解并不容易，然而通过观察R*的构造可以发现，对于给定的yj∈Y，B*(yj)仅用来构造R*的第j列，也就是说B*(yj)仅与R*的第j列有关系，因此要最大化R与R*的贴近度，不如转化为对于∀yj∈Y，最大化R与R*第j列之间的贴近度，即

由此，给出真域贴近模糊推理算法的基本原则。

真域贴近模糊推理原则(FMP)设X与Y是非空集合，A，A*∈F(X)，B∈F(Y)，则FMP问题的解B*是使对∀yj∈Y(2)式均成立的F(Y)中的模糊集。

注:1)FMT问题的真域贴近模糊推理可以转化成FMP问题的真域贴近模糊推理，即

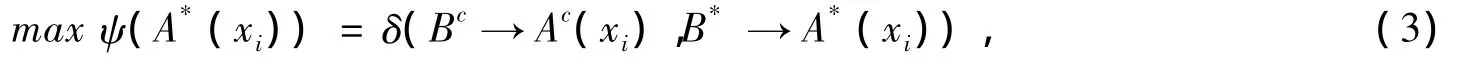
其中，Ac，Bc为A与B的补集。

2)满足(2)式的模糊集有时并不唯一，选择哪一个作为最终的推理结果建议结合贴近度函数及蕴涵算子进行考虑。

2 真域贴近模糊推理算法与CRI方法

单点模糊化是实际中最常用的，也是最简单的一种模糊化方法。设论域为X，输入变量为x*，采用单点模糊化方法，则有

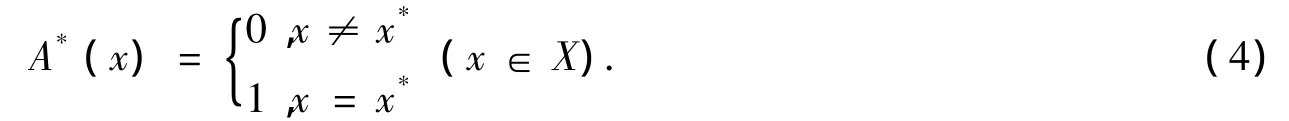
下面，考虑采用单点模糊化的真域贴近模糊推理算法及CRI方法。

定理1设X与Y是非空集合，A∈F(X)，B∈F(Y)，A*为满足(4)式的模糊集，若蕴涵算子I满足对∀b∈［0，1］，I(0，b)=c(c为常数)且映射f(b)=I(1，b)为关于b的双射，则满足(2)式的模糊集为

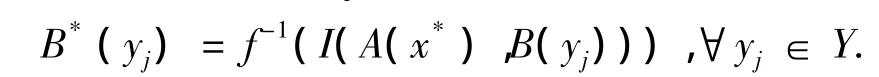
证明:∀yj∈Y，利用蕴涵算子I将A→B(yj)和A*→B*(yj)表示成向量形式，设分别为

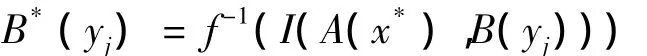
时，Rj与的贴近程度最大。

推论1设X与Y是非空集合，A∈F(X)，B∈F(Y)，A*为满足(4)式的模糊集，若蕴涵算子I满足对∀b∈［0，1］，I(0，b)=c(c为常数)且I(1，b)=b，则满足(2)式的模糊集为B*(yj)=I(A(x*)，B(yj))，∀yj∈Y。

定理2设X与Y是非空集合，A∈F(X)，B∈F(Y)，A*为满足(4)式的模糊集，I为蕴涵算子，采用CRI方法的FMP问题的解为

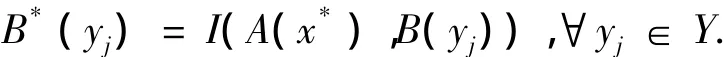
证明:对∀xi∈X，yj∈Y，R(xi，yj)=I(A(xi)，B(yj))，B*=A*°R，因此，

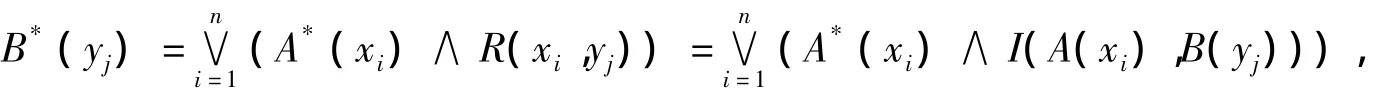
注意到(4)式，因此有B*(yj)=I(A(x*)，B(yj))。

事实上，许多常用的蕴涵算子，如

Mamdani蕴涵:RM(a，b)=a∧b，Zadeh蕴涵:RZ(a，b)=(1－a)∨(a∧b)，

Lukasiewicz蕴涵:RLK(a，b)=1∧(1－a+b)，Gougen蕴涵均满足推论1所需的条件∀b∈［0，1］，I(0，b)=c及I(1，b)=b。对比推论1与定理2可知，当蕴涵算子满足∀b∈［0，1］，I(0，b)=c及I(1，b)=b时，采用单点模糊化的真域贴近模糊推理算法与CRI方法的推理结果是一致的，这从侧面反映了CRI方法具有某些合理性。

3 采用最大－最小贴近度的真域贴近模糊推理算法

本节考虑采用最大－最小贴近度(简称δ1贴近度)

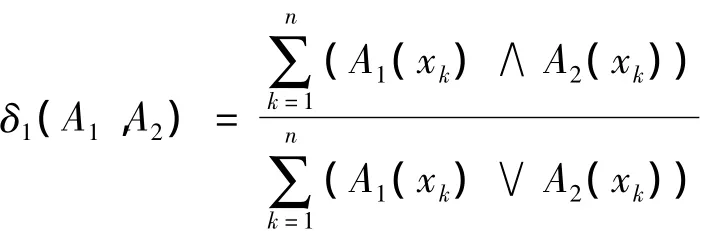
的真域贴近模糊推理算法。

上文提到，满足(2)式的模糊集有时并不唯一，对于δ1型真域贴近模糊推理算法给出如下的结果选择策略:

1)若蕴涵算子I满足I(0，b)=I(a，0)=c(a，b∈［0，1］，c为常数)，那么选择满足(2)式的最小模糊集;

2)若蕴涵算子I满足I(0，b)=I(a，1)=c(a，b∈［0，1］，c为常数)，那么选择满足(2)式的最大模糊集。

在这一策略下，当给定事实A*偏离规则前件A太多时，推理结果为可分辨的无意义或者无信息的结果，如B*=Y或者B*=∅。这样，在实际问题中将无意义或无信息的推理结果过滤掉，就可以得到正确的推理结果。下面给出采用δ1贴近度及RM、RZ、RLK、RGG的真域贴近模糊推理算法及其还原性。

定理3(δ1＆RM型真域贴近模糊推理算法)设X，Y为非空集合，A，A*∈F(X)，B∈F(Y)，则满足(2)式的最小模糊集为

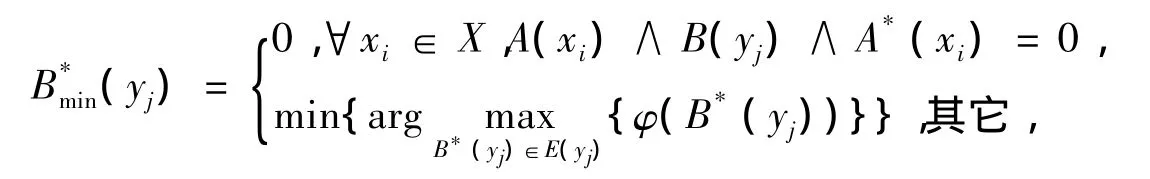
其中，E(yj)={0，1}∪{A(xi)∧B(yj)∧A*(xi)|xi∈X}∪{A*(xi)|xi∈X}。

定理4设X，Y为非空集合，A∈F(X)，B∈F(Y)，则δ1＆RM型真域贴近模糊推理算法满足还原性当且仅当对∀yj∈Y，B(yj)满足下面两个条件之一:

1)∃xk∈X，使得B(yj)＜A(xk);

2)B(yj)=。

定理5(δ1＆RZ型真域贴近模糊推理算法)设X，Y为非空集合，A，A*∈F(X)，B∈F(Y)，则满足(2)式的最大模糊集为

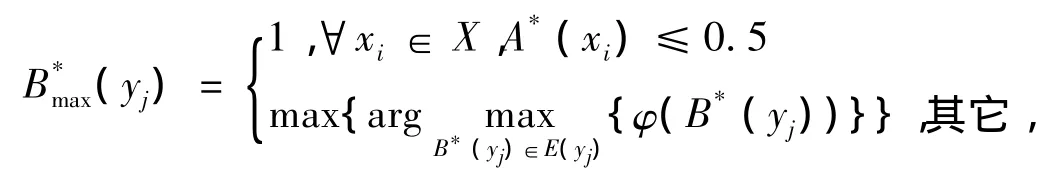
其中，

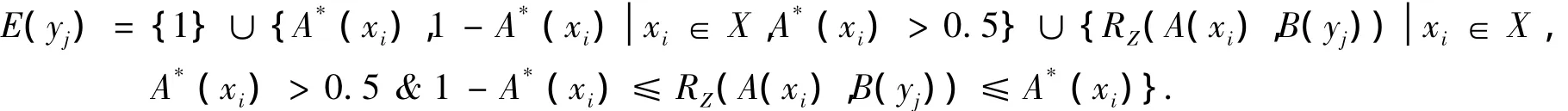
定理6设X，Y为非空集合，A∈F(X)，B∈F(Y)，则δ1＆RZ型真域贴近模糊推理算法满足还原性当且仅当对∀yj∈Y，B(yj)满足下面两个条件之一:

1)∃xk∈X，使得A(xk)＞0.5＆1－A(xk)≤B(yj)＜A(xk);

2)B(yj)=1。

定理7(δ1＆RLK真域贴近模糊推理算法)设X，Y为非空集合，A，A*∈F(X)，B∈F(Y)，则满足(2)式的最大模糊集为

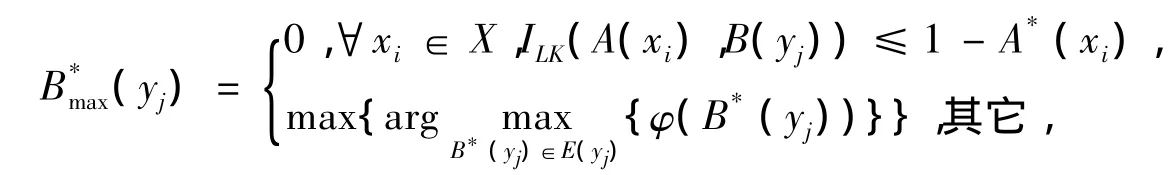
其中，

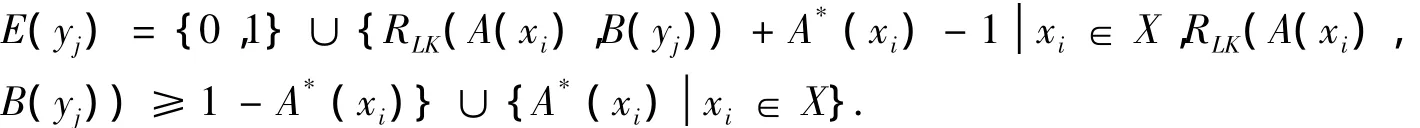
定理8设X，Y为非空集合，A∈F(X)，B∈F(Y)，则δ1＆RLK真域贴近模糊推理算法满足还原性当且仅当对∀yj∈Y，B(yj)满足下面两个条件之一:

1)∃xk∈X，使得B(yj)＜A(xk);

2)B(yj)=1。

定理9(δ1＆RGG真域贴近模糊推理算法)设X，Y为非空集合，A，A*∈F(X)，B∈F(Y)，则满足(2)式的最大模糊集为

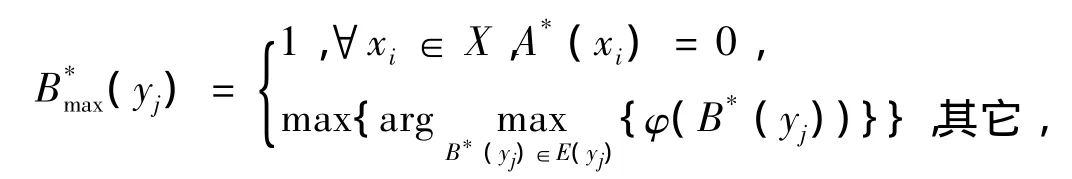
其中，E(yj)={RGG(A(xi)，B(yj))·A*(xi)，A*(xi)xi∈X}∪{1}。

定理10设X，Y为非空集合，A∈F(X)，B∈F(Y)，则δ1＆IGG真域贴近模糊推理算法满足还原性当且仅当对∀yj∈Y，B(yj)满足下面两个条件之一:

1)∃xk∈X，使得B(yj)＜A(xk);

2)B(yj)=1。

由定理4、定理6、定理8及定理10可知，若模糊集A为正规模糊集，即∃xk∈X，使得A(xk)=1，则采用RM、RZ、RLK、RGG的δ1型真域贴近模糊推理算法均为还原算法。事实上，对于满足I(1，b)=b，∀b∈［0，1］的蕴涵算子I，若A为正规模糊集，则δ1＆I型真域贴近模糊推理算法为还原算法。

定理11设X，Y为非空集合，A∈F(X)，B∈F(Y)，蕴涵算子I满足I(1，b)=b，∀b∈［0，1］，如果A为正规模糊集，则δ1＆I型真域贴近模糊推理算法满足还原性。

当然，A为正规模糊集仅是δ1＆I型真域贴近模糊推理算法满足还原性的一个充分条件，事实上可以将这个条件进一步扩展。

定理12设X，Y为非空集合，A∈F(X)，B∈F(Y)，若存在xk∈X，使得g(b)=I(A(xk)，b)为关于b的单调函数，则δ1＆I型真域贴近模糊推理算法满足还原性。

4 真域贴近模糊推理算法与CRI方法及全蕴涵三I算法的比较

CRI方法及全蕴涵三I算法(简称三I算法)是两种广受关注的模糊推理算法，其中，CRI方法因其简单易于实现的特点，被广泛应用于模糊控制等许多实际问题，而三I算法具有较好的逻辑语义特性，目前是模糊推理领域研究的热点内容。本节我们将通过实验对比真域贴近模糊推理算法与CRI方法及全蕴涵三I算法的推理能力，其中蕴涵算子使用上节提到的RM、RZ、RLK、RGG四种蕴涵算子，相应的三I算法使用文献［18］的结论。

设A为定义在［0，16］上的模糊集，B为定义在［0，12］上的模糊集，如图1所示。

推理规则依然为If x is A，then y is B，设输入模糊集A*为如下四种情形:

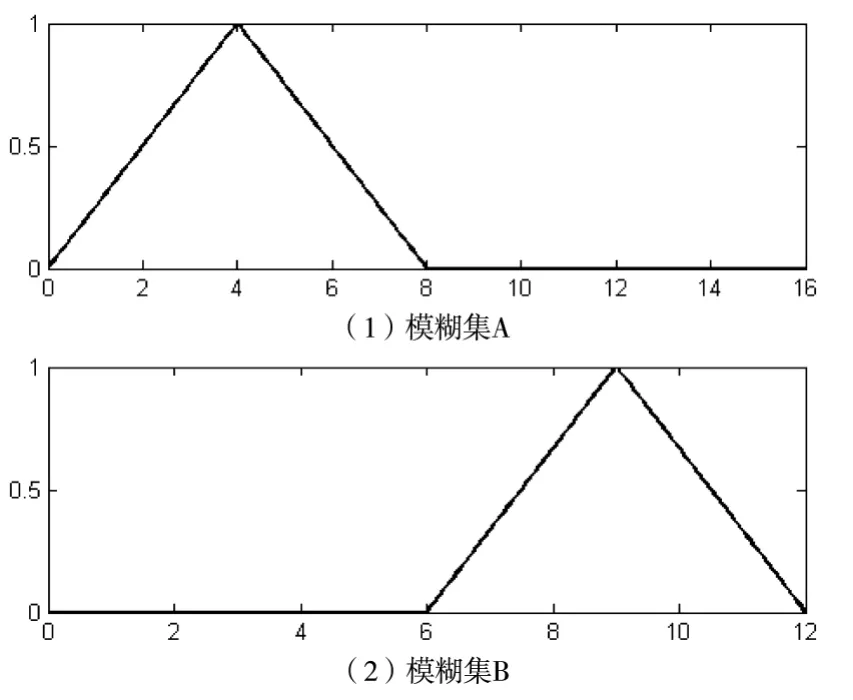
图1 模糊集A与B

1)A*=很A=A2;2)A*=略A=;

3)A*=A左倾;4)A*=A右倾很多。

具体如图2所示。这里，我们没有考虑A*=A的情

形，即考虑算法的还原性问题，事实上由于A为正规模糊集，因此三I算法及真域贴近模糊推理算法均满足还原性的条件。

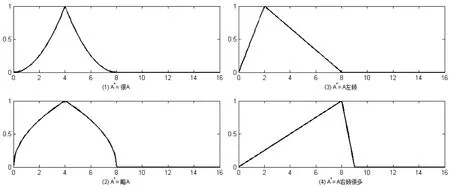
图2 模糊集A*

1)采用Mamdani蕴涵，分别计算使用CRI方法、三I算法以及真域贴近模糊推理算法的推理结果，如图3所示，其中OS表示真域贴近模糊推理算法。

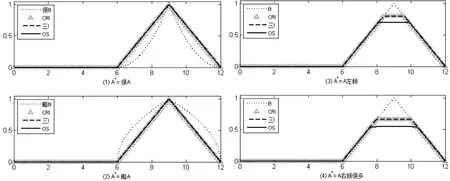
图3 采用Mamdani蕴涵的推理结果

由图3可以看出，采用Mamdani蕴涵时，若A*为很A或者略A时，这三种方法得到的推理结果都不是期望的很B或者略B，由此可见Mamdani蕴涵不适用于这种类型的模糊推理。当A*为A左倾或右倾时，CRI方法与三I算法的推理结果是一样的，真域贴近模糊推理算法的结果略小于CRI及三I算法的推理结果。由于算法无法判断推理结果B*应当左倾或右倾，因此推理结果没有明显的倾向性这是合理的，实际问题中通过规则库及合适的去模糊化方法均会得到合理的推理结果。

2)采用Zadeh蕴涵，分别计算使用CRI方法、三I算法以及真域贴近模糊推理算法的推理结果，如图4所示。

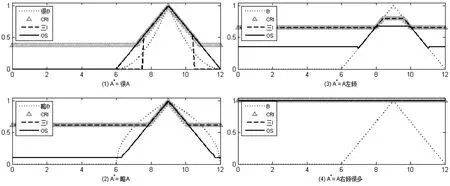
图4 采用Zadeh蕴涵的推理结果

由图4可以看出，无论哪种情形，采用Zadeh蕴涵的推理结果都不是十分理想，当A*为很A或者略A时，真域贴近模糊推理算法得到的结果能够尽量维持为B或B附近，而CRI方法及三I算法的推理结果已经偏离B很多。当A*为A左倾时，CRI方法及三I算法的推理结果接近一条直线，推理结果已经没有太多意义。当A*为A右倾很多时，这三种推理方法得到的结果均为B*=Y，但是需注意真域贴近模糊推理算法得到的结果与CRI方法及三I算法存在着不同，CRI方法及三I算法得到B*=Y是由于存在点xi∈X，使得A(xi)=0且A*(xi)=1，这也是CRI方法及三I算法的一个弊端，而真域贴近模糊推理算法得到B*=Y是由于A*偏离A较多的缘故，此时算法认为A*与A贴近程度不高，所得推理结果B*=Y为便于分辨的无意义结果，这种情形在后边两个蕴涵算子中也有体现。

3)采用Lukasiewicz蕴涵及Gougen蕴涵，分别计算使用CRI方法、三I算法以及真域贴近模糊推理算法的推理结果，如图5及图6所示。

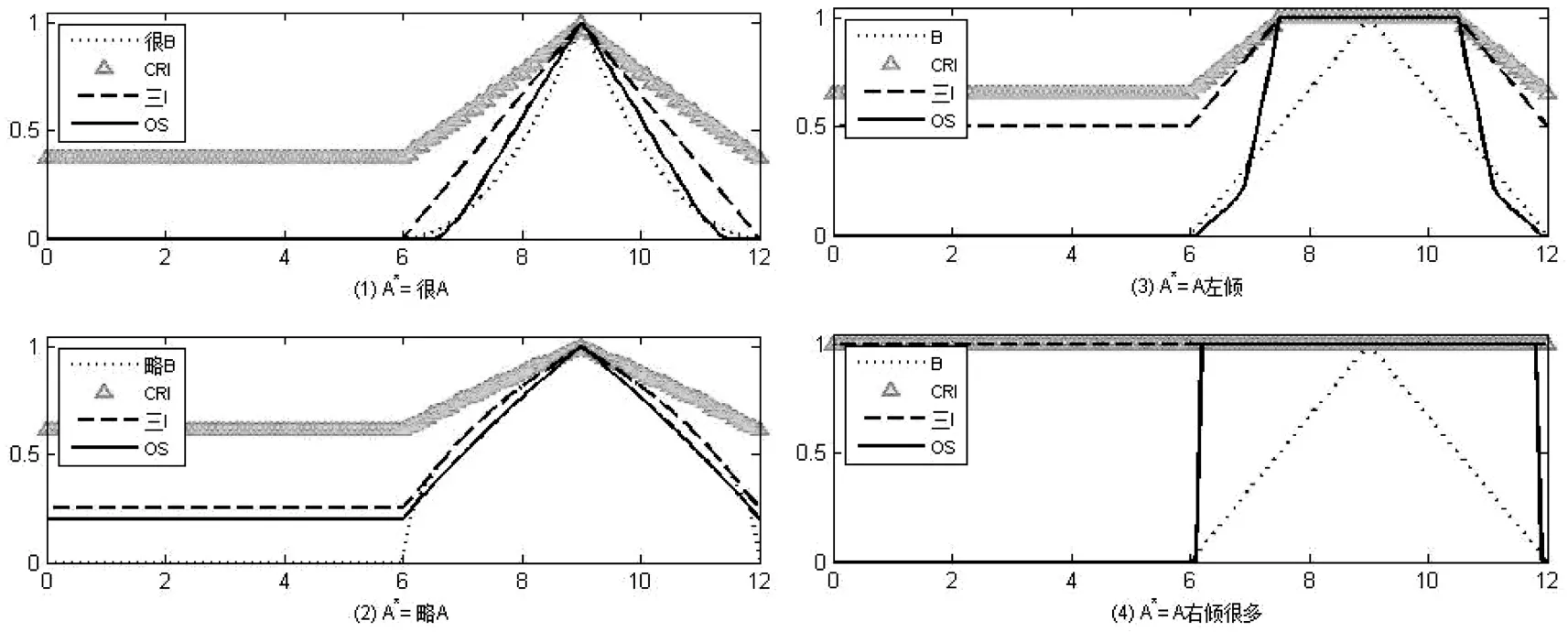
图5 采用Lukasiewicz蕴涵的推理结果

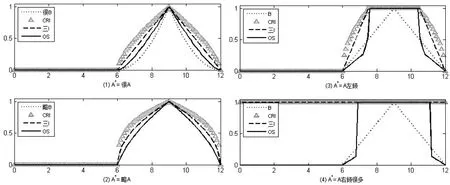
图6 采用Gougen蕴涵的推理结果

由图5及图6可以看出，采用Lukasiewicz蕴涵及Gougen蕴涵的真域贴近模糊推理算法推理结果明显要好于CRI方法及三I算法，当A*为很A时，推理结果接近于很B;当A*为略A时，推理结果接近于略B;当A*为A左倾或A右倾很多时，推理结果也相对合理。

从以上的实验可以看出，与CRI方法及三I算法相比，真域贴近模糊推理算法具有较好的推理能力，如果采用恰当的蕴涵算子，如Lukasiewicz蕴涵或Gougen蕴涵时，可以满足多种情形的模糊推理问题。

5 结论

本文提出并研究一种新的模糊推理算法，称为真域贴近模糊推理算法，其基本思想是通过最大化真域的贴近度来获取推理结果。基于这一思想，给出真域贴近模糊推理的基本原则，并以单点模糊化为例分析了真域贴近模糊推理算法与CRI方法之间的关系，进一步地，给出采用最大－最小贴近度的真域贴近模糊推理算法。最后，本文构建实验比较真域贴近模糊推理算法、三I算法以及CRI算法的推理能力。真域贴近模糊推理算法是一种全新的模糊推理算法，其思想简单自然，推理算法具有一定的逻辑基础，而且通过实验比较可以看出真域贴近模糊推理算法具有较好的推理能力。接下来，我们将分析真域贴近模糊推理算法的函数逼近性;构造模糊系统的响应能力;真域贴近模糊控制器的构建及应用等等。

［1］赵君，冯玉昌，赵柏林.模糊免疫PID在电站主汽温控制系统中的应用［J］.东北电力大学学报，2012，32(3):42－45.

［2］刘寅东.基于两级Smith预估的纯滞后系统串级模糊控制仿真［J］.东北电力大学学报，2012，32(3):46－48.

［3］L.A.Zadeh.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems，Man and Cybernetics，1973，3(1):28－44.

［4］E.H.Mamdani.Application of fuzzy logic to approximate reasoning using linguistic Synthesis［J］.IEEE Transactions on Computers，1977，26(12):1182－1191.

［5］李洪兴.模糊控制的插值机理［J］.中国科学(E辑)，1998，28(3):259－267.

［6］王国俊.模糊推理的全蕴涵三I算法［J］.中国科学(E辑)，1999，29(1):43－53.

［7］J.F.Baldwin.A new approach to approximate reasoning methods［J］.Fuzzy sets and systems，1979，2(4):309－325.

［8］I.B.Turksen，Z.Zhong.An approximate analogical reasoning approach based on similarity measures［J］.IEEE Transactions on Systems，Man and Cybernetics，1988，18(6):1049－1056.

［9］S.M.Chen.A new approach to handling fuzzy decision－making problems［J］.IEEE Transactions on Systems，Man and Cybernetics，1988，18(12):1012－1016.

［10］汪培庄，张洪敏.真值流推理及其动态分析［J］.北京师范大学学报，1989(1):1－12.

［11］张宇卓，李宇成，李洪兴.模糊推理的变权综合算法及其构造的模糊系统响应能力分析［J］.模糊系统与数学，2006，20(6):66－72.

［12］赵海良.简易插值模糊推理方法［J］.模糊系统与数学，2010，24(6):12－20.

［13］邹祥福，裴道武.模糊推理的SIS算法［J］.模糊系统与数学，2010，24(6):1－7.

［14］陈文伟，黄金才.基于神经网络的模糊推理［J］.模糊系统与数学，1996，10(4):26－30.

［15］K.Y.Cai，L.Zhang.Fuzzy reasoning as a control problem［J］.IEEE Transactions on fuzzy systems，2008，16(3):600－614.

［16］邓冠男.模糊推理算法的研究进展［J］.东北电力大学学报，2013，33(6):64－70.