数学估计及中国数学课程标准对其的培养要求

沈 威，曹广福

（广州大学 数学与信息科学学院，广东 广州 510006）

数学估计及中国数学课程标准对其的培养要求

沈 威，曹广福

（广州大学 数学与信息科学学院，广东 广州 510006）

摘要：数学估计包括定量数学估计和定性数学估计两类.定量数学估计分为3个方面：估数，估算和估测.而对定性数学估计的研究尚没有研究者涉及，经过探究发现，定性数学估计既是认知对象，也是元认知的重要成分.中国数学课程标准对数学估计能力的培养要求是从以定量数学估计为主向以定性数学估计为主方向发展，开发适合于不同学段的教学材料和教学策略是今后数学估计研究的重要任务之一.

关键词：估计；估数；估测；估算；定量数学估计；定性数学估计

估计（Estimation）在美国早已被列入数学课程标准[1~6]，1980年美国数学教师理事会（NCTM）在《行动的纲领》中建议“教师应该经常地有规律地将估计（Estimation）活动结合到数学程序中去，特别地，应鼓励学生在提出和选择对象以及研究结果的合理性时进行估计练习.”1990年NCTM颁发了《美国中小学数学课程标准》，把估计作为“数学的合法部分”，将估计能力作为一条重要的标准.中国在2001年由教育部颁布了《义务教育数学课程标准（实验稿）》，将估算（Computational Estimation）纳入小学数学教学内容，与“口算”、“计算”地位并重.自从估算被列入2001年《义务教育数学课程标准（实验稿）》便受到中国教育研究者的高度关注，既有数学教育内部的研究者[7~13]，也有数学教育外部的研究者[14].从已有研究文献来看，估计与估算混用常有出现，这样不但不利于对估算的理论研究和教学实践，而且容易混淆估计与估算的本质.研究拟对与数学学习有关的数学估计研究及中国数学课程标准对其的培养要求作一探讨.

1　数学估计

估计是重要的数学活动之一，也被认为是数感的重要组成部分[15].Beishuizen[16]认为快速而相对准确的估计能力有两个好处：一是可以让学生通过其他方式检查自己答案的合理性；二是可以帮助学生发展较好的位值理解、数学操作和一般数感.

鲍建生[6]对估计做了深入细致的研究，他认为“对估计的研究还不够广泛和深入，国外（主要是美国）的讨论基本集中在估算这一比较狭窄的范围内，而国内对此的研究更少.”“估计常被等同于估算，而估算又常常局限于近似计算，这是一种片面的看法，实际上，估计是人类的一种最频繁的心理活动.”鲍建生认为估计至少包括5种类型的估计：日常生活中的估计；测量中的估计；有效的精确度；价值性估计；利用计算机的估计.他总结了估计的3个特点：一是估计是一种介于推理和猜想之间的心理活动；二是估计是一种开放性的创造活动；三是估计是一种实用性的社会活动.

据此可以归纳出估计的一些本质特征：运用已有经验；结合实际情境；相对快速；满足一定条件；是心理活动；估计的结果是产生一个判断.所以，估计可以界定为：估计是主体结合实际情境运用已有经验产生一个相对快速且满足一定条件的判断的心理加工过程.把估计运用于不同的领域便表现出相应领域的估计特征，把估计运用于数学领域则表现出数学的估计特点.因此，数学估计是主体结合实际情境运用已有的数学经验产生一个相对快速且满足一定条件的数学判断的心理加工过程.从数学估计产生的结果来看，有的数学估计是获得一个量的判断，有的数学估计是获得一个猜想、思路或方法等非量的判断，称前者为定量数学估计，后者为定性数学估计.

2　定量数学估计

从现有研究来看，主要涉及3种定量数学估计类型：数量估计（numerical estimation简称估数）、测量估计（measurement estimation简称估测）和计算估计（computational estimation，简称估算）[17].

2.1对估数的研究

估数被认为是一种有关数字判断的数学问题解决形式，是灵活运用数学知识的一种适应性问题解决方式.估数实际是在没有足够时间数出物体的数量，或要数的物体数量过大，或对非静止的物体根本无法做出计数的情况下做出一种粗略估计，是一种高层次的认知加工过程[18].估数的研究主要涉及估数的精确性、表征方式和策略.研究表明，估数的精确性随年龄的增长而提高；物体特性、时间向度和空间向度是影响个体数量估计精确性的主要因素，物体的大小、图形形状和规则性等物体特性均影响数量估计的精确性.

司继伟[19]认为不同数学学业水平小学生数量估计准确性存在显著差异，优生的估计准确性显著高于差生；图形排列方式不同对儿童数量估计的准确性会产生显著影响.均匀排列的图形会比不均匀排列的图形高估；规则排列的图形会比随机排列的图形高估.在表征方式研究上，目前主要认为个体对数量估计的表征存在两种模型：对数规则模型和累积模型.对数规则模型认为人类和其他动物一样依靠单一的对数规则进行表征；累积模型则认为所有的人都把数量表征为随数量的增加呈线性增长.尽管这两种模型为人类及其他如何进行数量表征提供了有力的解释，但似乎还没有一种模型能够完整描述人们进行数量表征时所使用的表征方式.在估数策略上，人们倾向于使用3种策略：相加、相减和估计[18].

2.2对估测的研究

估测是一种非常实用的日常数学技能，主要包括对长度、面积、重量、温度和价格等日常数学范畴的估计[20].Bright将估测界定为“在不使用一般的测量工具的情况下，以某种方法推测出测量结果的一种心理加工过程”[21].估测研究主要包括估测能力发展及影响因素和估测的策略.已有研究成果已经初步揭示了个体估测能力发展的趋势，发现个体在估测能力上，从小学到中学，从低年级到高年级，是不断发展的，成人的估计能力比学生好许多；也有研究显示估测能力可能与性别有一定关系，即男性在估计距离和高度时要好于女性，但是估计重量和温度时则没有发现类似情况[20].庄维展的研究结果却显示男女儿童在面积、长度、容量、重量等4种估测任务上的表现并无明显差别[22].关于估测的策略，一般认为，常见有效估测策略大体可分为3类：单位迭代、参照点（又称基准点）、在估计前把估计物进行心理转换.单位迭代是指估计者在估计时，使用某个标准单位（如厘米），反复将标准单位与估计物相对照，记住上次标准单位结束的位置，开始下一次对照，计算单位的数目，从而得出估计结果.这种策略要求估计者在估计时若没有呈现单位，需要回忆这个单位并对估计物进行分解.在已发现的估测策略中，单位迭代运用得最为普遍[20].

司继伟对青少年估测能力的发展状况进行了研究[23]，认为：（1）青少年的总体估测能力普遍较低；（2）青少年的估测能力在初中阶段会显著提高，但之后的发展相对缓慢；（3）青少年的估测成绩易受任务类型和题目形式的影响，对长度任务的估测成绩好于对面积的估测；对图形题目的估测成绩好于对实际物体的估测；（4）青少年的估测能力不存在明显性别差异.

2.3对估算的研究

比起估数和估测，关于估算的研究成果相对较多.司继伟对小学儿童估算能力做了深入的研究，他把估算界定为“个体未经过精确计算而只借助原有知识对问题提出粗略答案的一种估计形式，是心算、数概念和算术计算技巧之间相互作用的过程”[24].司继伟认为小学儿童的估算能力存在非常明显的题目类型差异，他们给估算值距离精确值的偏离程度随问题难度上升而逐渐增加；三年级可能是整数和小数估算能力发展的一个关键期，而五年级则是分数估算能力发展的较好时期；在不同问题特点影响下，小学儿童的估算成绩随问题难度上升而明显下降，数字大小、调整幅度和问题形式等问题特征都对估算速度有明显影响，实际背景中多余条件的出现会明显延长儿童的估算时间等.

陈丽兰研究了9~12岁儿童估算策略选择的发展特点[25]，她认为儿童在估算时选择了多种策略，且策略的使用频率并不相同，取整使用最频繁，其次是先补偿，转换和分解策略的使用频次最小；随着问题特征难度的增加，估算策略选择的最佳击中率降低；随着年龄的增长，估算策略选择的个数增加，估算策略选择的最佳击中率上升，其中四、五年级儿童的最佳击中率上升尤为显著；估算策略的选择不存在性别差异.

张云仙对学业不良生与学优生的估算能力做了比较研究[26]，她认为：（1）数学学业不良儿童的整数和小数的估算成绩没有达到显著差异，但都与分数估算成绩达到显著差异，分数估算成绩最差，等级性估算成绩显著好于参考数估算和开放式估算成绩，但参考数估算和开放式估算成绩差异不显著；（2）学优儿童的整数估算成绩显著高于小数成绩，而小数估算成绩又显著高于分数成绩，等级性估算成绩显著高于参考数估算成绩，开放式的估算成绩也显著好于参考数估算成绩；（3）学业不良儿童与学优儿童比较，更容易犯盲目猜测错误、运算规则执行错误、小数点位置错误和位值错误.

虽然估算的研究文献相对多些，却对估算没有形成统一认识.例如张奠宙认为：小学估算的基础是精确计算，没有精确度的估算是“胡算”[13]；而司继伟则认为：估算是个体未经过精确计算而只借助原有知识对问题提出粗略答案的一种估计形式，是心算、数概念和算术计算技巧之间相互作用的过程[24].事实上，他们对估算的界定都只抓住了估算的某一个方面，并没有从数学的全貌来研究估算，从而他们的界定都有失偏颇.针对张奠宙的界定，在小学阶段有“401接近一个什么样的数？”的问题，这不需要精确计算，只要比较或观察就可以得到401接近400的结果，所以这种估算不是在精确计算的基础上；针对司继伟的界定，在解决问题过程中，往往不能直接得到结果，要在一定严格演绎计算基础上可以通过估算把握结果，这是是建立在严格的逻辑演绎基础上的估算，例如，函数极限的e-d中的d确定就是在严格精确计算基础上估算的.因此，估算可以进一步界定为：估算是主体结合数学情境运用已有数学计算经验产生一个相对快速且满足一定条件的、与计算有关的、判断的心理加工过程.

2.4对定量数学估计能力的研究

刘效贞[27]等以数学估计由估数、估测和估算3种类型构成为依据，研究了初中生的数学估计能力及其与元认知监控的关系.经过研究发现：（1）中国初中生的估计能力发展相对不充分，在估数、估测、估算等任务上得分均较低.初二学生在不同估计任务中的表现相对较好；在估算任务中，男生的表现显著优于女生.估计能力从整体上并无稳定的性别差异.（2）元认知的4个维度与估计表现均存在显著正相关.自我意识维度可以显著正向预测估计表现，是估计表现的一项良好的预测指标.具体来说，计划维度可以正向预测估数和估算表现，而自我意识维度可以正向预测估测和估算表现.

2.5对定量数学估计心理模型的研究

Alexander[28]认为数学估计由估算与估测构成，并根据实验研究建构了数学估计的心理模型（如图1），他根据研究解构把数学估计心理模型分为相关的两类：参照估计和解构/重构估计.参照估计是个体知道参照标准于运用被估计项目（To-Be-Estimated item (TBE)）的过程；对于一些估计问题没有参照标准可用时，主体第一步要把TBE解构为足够小的样本以至于运用参照估计，然后再重构这些样本得到最终的估计.Alexander研究了6种类型的估计问题：整数长度参照估计，分数长度参照估计，正则长度解构/重构估计，正则数字解构/重构估计，非正则长度解构/重构估计，非正则数字解构/重构估计.根据研究结果，他建构出如下的数学估计心理模型.

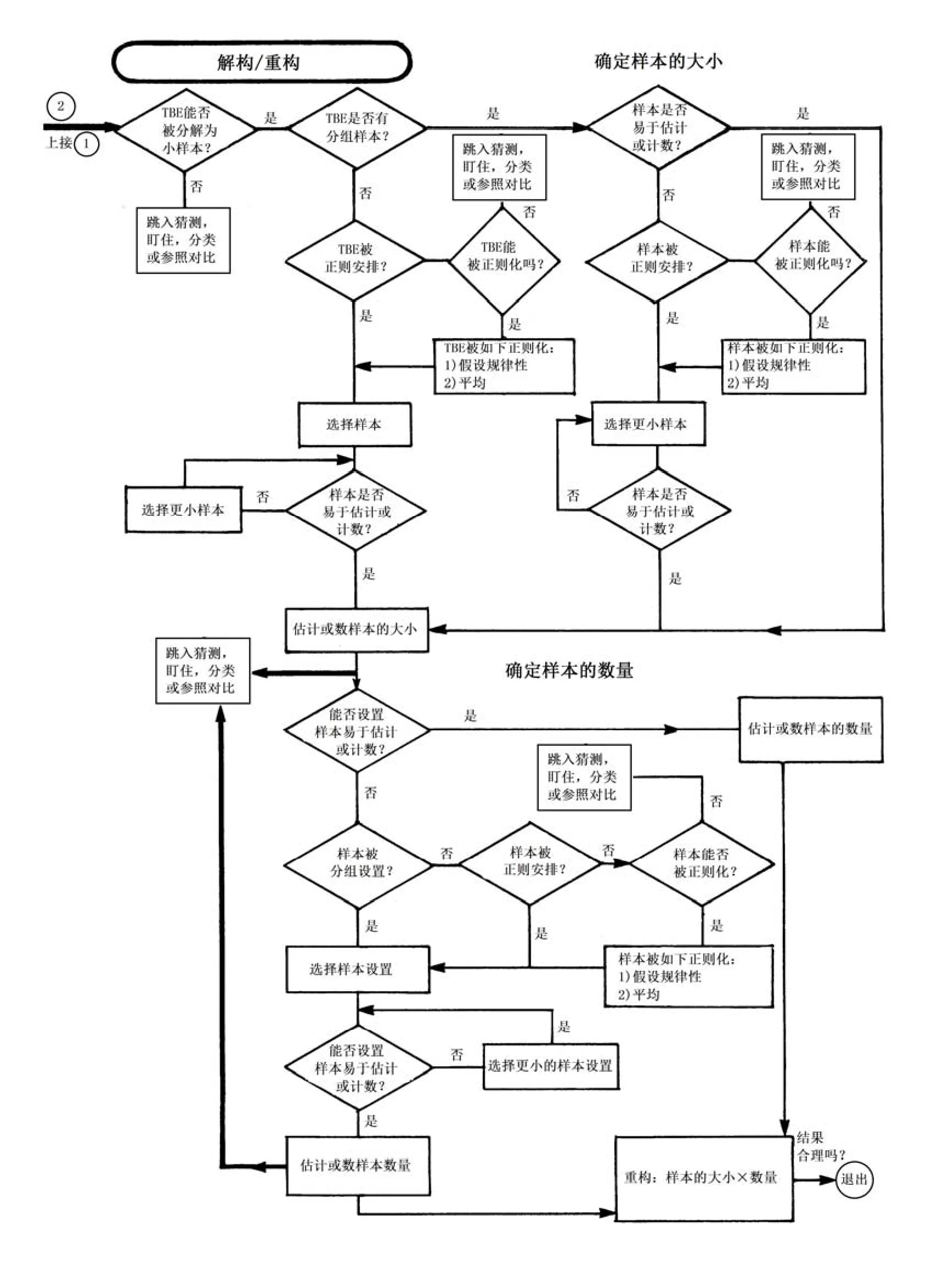
图1　估计模型

3　定性数学估计

目前所讨论的数学估计都是定量数学估计，与定量数学估计相对应的是定性数学估计，对定性数学估计的研究尚没有研究者涉及，但是定性数学估计在数学问题解决或数学研究过程中无处不在.定性数学估计不但作为认知的直接对象，还是监控认知过程的元认知的重要成分.

作为认知对象，定性数学估计在数学问题解决或数学研究中的表现之一则是猜想.解题者在问题解决过程中，经过一定的逻辑演绎的计算或推理，对逻辑演绎的非数字结果做出估计，估计演绎结果的结构与特征，这种估计的结果就是猜想.定性数学估计的表现之二则是对解题模式或解题方法的估计.题者在问题解决过程中，经过一定的逻辑演绎的计算或推理，对接下来的计算或推理做出估计，估计下一步或若干步计算或推理需要的方法，估计下一步或若干步计算或推理需要的解题模式.定性数学估计的表现之三则是统计估计，即研究者在获得一定的统计数据的基础上，根据数据所反映的某种统计规律或特点对今后一段时间发生该情况做出估计，不同的研究者对同一现象的统计结果是不同的，有些研究者的估计比较准确，而有些研究者的估计却欠准，这也反映了统计研究者估计能力的不同.

作为元认知成分，估计就是预见的主要成分，在元认知监控过程中，预见是非常重要的，通过预见主体可以把自身置于非常有利的位置上.例如，在数学解题的整个过程，主体随时估计自己的处境，判断问题的性质，展望问题的前景.对数学问题的性质、特点和难度以及解题的基本策略和基本思维做出大致的估计、判断和选择；猜想问题的可能答案和可能采取的方法，并估计各方法的前景和成功的可能性等，要设法使自己置身于一个最便于行动的位置上，处在一个最易于抓住问题的位置上[29].事实上，定性估计离不开定量估计，定量数学估计也离不开定性数学估计，而定性数学估计是发明创造的基础，从某种意义上讲，定性数学估计要比定量数学估计更加重要.

4　中国数学课程标准对数学估计能力的培养要求

数学估计是一种重要的数学能力，培养学生的数学估计能力显得非常必要与迫切.表1列出了《义务教育数学课程标准（2011）》[30]和《普通高中数学课程标准（实验）》[31]对数学估计的课程要求，从中能够看出中国数学课程标准对数学估计能力培养的重点与规律.

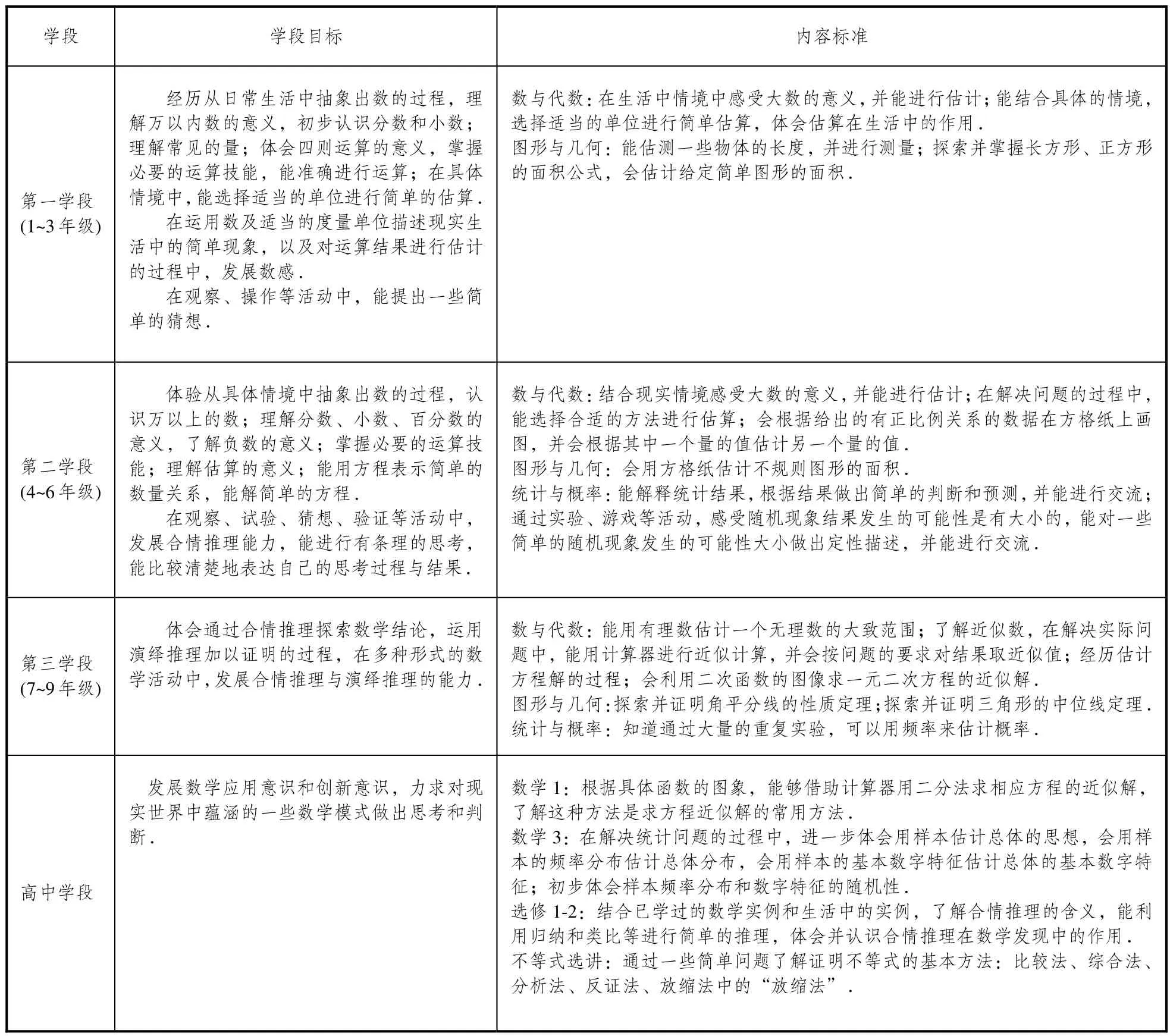
表1　中国数学课程标准对数学估计能力的培养要求

由表1可知，在第一学段，课程标准对数学估计能力的培养放在“数与代数”和“图形与几何”上，没有把数学估计能力的培养放在“统计与概率”上，这是由第一学段学生的认知水平决定的.第一学段学生的年龄小，其认知水平处于对确定性对象的认知，没有达到认识随机现象的认知水平.培养重点是定量估计，即与四则运算、度量单位、面积计算等有关的估测和估算.通过这些简单的定量估计发展学生的数感.第二学段，以定量估计为主，以定性估计为辅.在定量估计中，以估算为主，估测为辅；在定性估计中，主要是能对一些简单的随机现象发生的可能性大小做出定性描述.第三学段，定量估计和定性估计并重.定量估计主要表现在估计数的范围、求近似数等；定性估计表现为猜想、预测结论，用频率来估计概率等.高中阶段，以定量数学估计为辅、定性数学估计为主.定量数学估计表现为对近似数的估计，定性数学估计表现为对解题模式、方法的估计，对统计数据的估计，对合情推理结果的估计等.如果以同心圆环的面积表示各个学段数学估计能力的发展，由内向外扩张，前一学段的数学估计能力是后一学段发展的基础，随着学生学段的升高，其知识和认知能力也在不断提升，学生数学估计能力也发展得更高，整个大圆的面积就是学生数学估计能力发展的总体状况，图2可以表征中国数学课程标准对数学估计能力培养要求的模型.

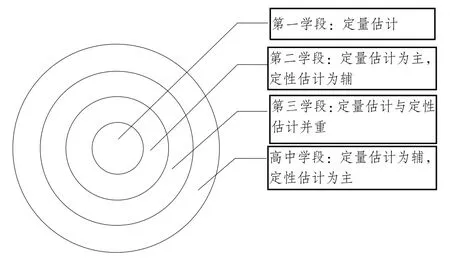
图2　中国数学课程标准对数学估计能力培养要求的模型

5　展 望

数学估计潜浸在人类的数学思维过程中，表现出数学估计无所不在，但是真正认识到数学估计及其价值比较晚，对数学估计开展相关研究的文献不多.从已有研究文献来看，数学估计的研究主要涉及估数、估测和估算3种类型，这3种类型的数学估计都是定量数学估计，即从量的角度研究数学估计；而比定量数学估计更加重要的定性数学估计更加需要深入研究.即便在定量数学估计中，是不是只含有估数、估测和估算3种类型？是否还有其他类型的定量数学估计？估数、估测和估算之间有何区别与联系？从中国《义务教育数学课程标准（2011）》对数学估计的培养要求看，只提到估算与估测，并没有把估数纳入课标体系.在《中国数学课程标准对估算要求的变化探析》[32]一文中，估算与估测等数学估计的概念之间关系表述不清，没有明确估计、大约、估测、推测等与估算之间的层级关系.因此，对有关数学估计的研究需要做出进一步探讨.

目前有关数学估计的研究比较松散，缺少对数学估计的系统理论研究，而且对一些核心概念还没有大致的统一认识，因此有必要对数学估计进行理论梳理，建构能被国内数学教育工作者基本认同的数学估计理论框架和分析框架.在相应的框架下析出相应的二级、三级或多级的数学估计层级概念，并保持内在的一致性.研究各层级可检测的行为指标，通过可检测的行为指标使得数学估计便于把握和研究，根据各级指标制定相应的各年级或各学段量表，这样能够正确测量目前中国学生数学估计能力的水平，为教学提供客观依据.研究数学估计的目的是促进学生数学估计能力的发展，因此，要根据数学估计的研究成果开发促进学生数学估计能力发展的教学策略.从上述的讨论来看，小学生、中学生对数学估计能力发展的需要是不同的，小学生的估计能力发展偏重以定量数学估计为主，随着年龄的增长，应该逐渐从培养定量数学估计能力为主过渡为培养定性估计数学能力为主，所以对不同年龄或不同学段学生的数学估计能力培养的教学材料和教学策略也是不同的，开发与不同年龄学生相适应教学材料和教学策略也是今后数学估计研究的重要任务之一.

［参 考 文 献］

[1]National Council of Supervisors of Mathematics. National Council of Supervisors of Mathematics Position Paper on Basic Mathematical Skills [EB/OL]. http://midcentral-coop.org/uploads/Basic%20Skills%20Position%20Paper.pdf. 1977.

[2]National Council of Supervisors of Mathematics. Essential Mathematics for the Twenty-first Century: The Position of National Council of Supervisors of Mathematics [EB/OL]. http://www.jstor.org/discover/10.2307/27966331?uid=37378 00&uid=2129&uid=2&uid=70&uid=4&sid=21103127658691. 1989.

[3]National Council of Teachers of Mathematics. Agenda for Action: Recommendations for School Mathematics of the 1980’s [EB/OL]. http://www.nctm.org/standards/content.aspx?id=17278. 1980.

[4]National Council of Teachers of Mathematics. Curriculum and Evaluation for School Mathematics [EB/OL]. http://www.mathcurriculumcenter.org/PDFS/CCM/summaries/standards_summary.pdf. 1989.

[5]National Council of Teachers of Mathematics. Principles and Standards for School Mathematics [EB/OL]. http://www.nctm.org/standards/content.aspx?id=16909. 2000.

[6]鲍建生.估计——数学教育面临的新问题[J].教育研究，1997，（10）：69-72.

[7]曹一鸣.从数学本质解读数学课程改革[J].数学教育学报，2005，14（1）：42-45.

[8]吴晓红.口算的本真意义及其在小学数学教学中的异化[J].数学教育学报，2005，14（2）：83-85.

[9]田中.4~7岁儿童空间认知和推理能力的测试研究[J].数学教育学报，2007，16（4）：35-41.

[10]杨豫晖.小学数学教材中数学史的内容及呈现方式探析[J].数学教育学报，2007，16（4）：80-83.

[11]戎松魁.关于人教版小学数学新教材中若干问题的思考[J].数学教育学报，2008，17（2）：58-60.

[12]汤服成.中学生数学元认知知识的调查研究[J].数学教育学报，2009，18（3）：39-41.

[13]张奠宙.小学数学中若干科学性问题的探讨[J].小学数学（教学版），2011，（1）：6-9.

[14]司继伟，张庆林.估算：来自心理学的心声[J].心理发展与教育，2002，（2）：38-42.

[15]Greeno J G. Number Sense as Situated Knowing in a Conceptual Domain [J]. Journal for Research in Mathematics Education. 1991, (22): 170-218.

[16]Beishuizen M, van Putten C M, van Mulken F. Mentalarithmetic and Strategy Use with Indirect Number Problems up to One Hundred [J]. Learning and Instruction, 1997, (1): 87-106.

[17]Koen Luwel, Lieven Verschaffel. Estimation of Real Numerosities in Elementary School Children [J]. European Journal of Psychology of Education, 2008, (3): 319-338.

[18]徐继红.数量估计研究的回顾[J].心理科学，2010，（3）：646-648.

[19]司继伟.不同数学水平儿童的数量估计：图形排列方式的影响[J].心理发展与教育，2008，（3）：84-88.

[20]司继伟.测量估计研究：回顾与展望[J].心理科学，2007，（6）：1 466-1 468.

[21]Swan M, Jones O. Comparison of Students. Percepts of Distance, Weight, Height, Area, and Temperature [J]. Science Education, 1980, (64): 297-307.

[22]庄维展.国小学童估量能力之分析研究——以高高屏三县市五年级学童为例[D].台湾屏东师范学院数理教育研究所，2001.

[23]司继伟.青少年测量估计能力的发展状况及相关因素[J].心理发展与教育，2010，（4）：351-356.

[24]司继伟.小学儿童估算能力研究[D].西南师范大学，2002.

[25]陈丽兰.9~12岁儿童估算策略选择的发展特点[J].数学教育学报，2012，21（1）：48-51.

[26]张云仙.学业不良生与学优生估算能力对比研究[J].数学教育学报，2008，17（4）：49-52.

[27]刘效贞.初中生的数学估计能力及其与元认知监控的关系[J].心理发展与教育，2009，（2）：35-40.

[28]Alexander W Siegel. Skill in Estimation Problems of Extent and Numerosity [J]. Journal for Research in Mathematics Education, 1982, (3): 211-232.

[29]涂荣豹.数学解题学习中的元认知[J].数学教育学报，2002，11（4）：6-11.

[30]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2011.

[31]中华人民共和国教育部.普通高中数学课程标准（实验）[M].北京：北京师范大学出版社，2003.

[32]孙卫红.中国数学课程标准对估算要求的变化探析[J].数学教育学报，2013，22（5）：27-31.

[责任编校：张楠]

Athematical Estimation and It’s Training Requirements in Our Country’s Mathematics Curriculum Standards

SHEN Wei, CAO Guang-fu
(School of Mathematics & Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

Abstract:Mathematical estimation including quantitative mathematical estimation and qualitative mathematical estimates. Quantitative mathematical estimation including: numerical estimation, measurement estimation, and computational estimation. The study of qualitative mathematical estimation that there is no the researchers involved, we found that Qualitative mathematical estimates is the cognitive object and important component of metacognition. Mathematics curriculum standards’ Training Requirements for mathematical estimation ability is from qualitative mathematical estimation to quantitative mathematical development.

Key words:estimation; numerical estimation; measurement estimation; computational estimation; quantitative mathematical estimation; qualitative mathematical estimation

作者简介：沈威（1982—），男，安徽灵璧人，博士生，讲师，主要从事数学课程与教学论研究.

基金项目：2014年教育部人文社会科学规划基金项目——我国农村中小学教师的TPACK及其教学表现研究（14YJA880054）；2014年广东省教育研究院一般项目——最新中美数学教材编写与数学教学特色研究（GDJY-2014-A-b210）

收稿日期：2015-03-10

中图分类号：G40-034

文献标识码：A

文章编号：1004-9894（2015）04-0033-07