多随机参数下的配电网多目标无功优化

张杭，丁晓群，何健，邓吉祥

(1.河海大学能源与电气学院，南京市 211100;2.国网河北省电力公司检修分公司，石家庄市 050070)



多随机参数下的配电网多目标无功优化

张杭1，丁晓群1，何健2，邓吉祥1

(1.河海大学能源与电气学院，南京市 211100;2.国网河北省电力公司检修分公司，石家庄市 050070)

针对实际中时序性负荷模型难以直接运用于无功优化的问题，提出基于枢轴量法的负荷建模新方法。由于配电网中多随机参数是并行的，提出基于贝叶斯公式时空解耦的配电网系统场景划分策略，建立多随机参数下的配电网多目标无功优化场景概率模型。最后运用改进的IEEE33标准节点测试系统验证上述模型的有效性，结果证明了此文方法是高效和灵活的。

配电网；多随机参数；贝叶斯公式；枢轴量法

0 引 言

当前关于含DG的配电网无功优化国内外已有较深入的研究，但大都集中在某一随机参数的随机特性对无功优化影响的研究，而多随机参数并行的研究很少。文献[1-2]采用P-Q模型进行确定性无功优化，未考虑DG出力的随机性；文献[3-5]运用Monte Carlo成功模拟了出力的随机性，但该方法无法反映风速变化的快速性，且相当耗时；文献[6-7]采用分时段法描述DG的间歇性和负荷的波动性，然而只能采用理想模型且当前的预测精度不高；文献[8-10]采用场景划分法分析了DG出力的变化，但均未考虑负荷的波动性。

针对上述无功优化未考虑多随机参数并行和实际负荷模型难以直接应用的不足，本文根据序性负荷模型，运用枢轴量法建立适用于无功优化的负荷概率模型。采用改进的场景分析法实现系统场景的精确划分，运用贝叶斯(Bayes)公式计算出各场景的场景概率，从而建立多随机参数下的配电网多目标无功优化模型，然后运用基于分解的多目标差分进化算法(MOEA/D)求解该模型。最后采用改进的IEEE33节点系统验证本文所提方法的可行性和有效性。

1 计及多随机参数动态变化的配电网场景概率模型

场景概率分析法[8-9]是将难以直接计算的不确定因素转化为多个易于计算的确定性场景问题，并运用场景概率来描述每个场景发生的频率。为体现多随机参数(DG出力的变化、负荷等)动态变化对无功优化的影响，本文建立了基于Bayes公式的配电网时空解耦场景概率模型。其中，风电场出力服从Weibull分布，光伏发电的光强以Beta分布描述，负荷的波动以参数未知的正态分布描述[11]。

1.1 多DG随机出力的场景划分

含DG出力的典型配电网中一般存在多个风电场和光伏电站，而不同DG出力的差别很大，因此有必要对多DG的场景划分法进行分析。风电场[10]中的风机处于同一区域，因而可以假设风机出力服从同一分布，仅考虑其切入/出风速、额定容量和额定风速的差异，先采用拉丁超立方进行抽样[12]，然后根据粗糙集理论消减拉丁超立方抽样产生的冗余风速场景，提高计算效率和样本拟合精度。风电场的场景可以根据各个风电机组的风速区间进行划分，其场景功率与场景概率为

(1)

(2)

实验之前大致选择了两种方法作为选择进一步优化实验的基础（方法见1.3.3），对所得样品前处理产物进行色谱分析，分析条件见1.3.2，实验所得的色谱图如图6所示。

(3)

(4)

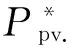
(5)

(6)

(7)

式中：N为DG出力总场景数；NDG为总的DG个数；Nl为第l个DG的独立场景数；Nw为风电场个数；Npv为光伏电站个数；Pi为第i个场景的DG场景功率向量；Pw.im和Ppv.in分别第i个场景下风电场m和光伏电站n的场景概率。

1.2 基于枢轴量法的负荷波动场景划分

本文采用解析法中的枢轴量法对负荷进行分析，假设系统负荷服从正态分布，正态分布的均值为负荷的预测值，方差采用枢轴量法[13]确定。设负荷总体X～N(μ，σ2)，选取的负荷样本为{X1，…，Xn}，选取置信度为1-α，μ已知，由概率统计的知识可知，样本方差是正态总体方差σ2的有效估计，因而可以选取样本方差为枢轴量；

(8)

(9)

式中：Sμ2为负荷样本方差；η为枢轴量；n为样本容量；χ2(n)为自由度为n的χ2分布。令置信度水平1-α和枢轴量η满足如下等式约束

(10)

由等式可以求出置信度为1-α时正态总体方差σ2的置信区间

(11)

得出正态总体方差的置信区间后，可按实际情况选取区间中点及边界点中的某一点作为正态总体的具体方差，一般选区间中点。根据概率论关于正态分布的理论，正态分布的取值为(-∞，+∞)，但落入区间(μ-3σ，μ+3σ)的概率为99.74%，故本文将正态分布离散化为7段作为负荷波动的场景划分如图1所示，各区间高度为各段中点值，区间概率为各段面积。

图1 离散化的正态分布Fig.1 Discrete normal distribution

1.3 基于Bayes公式的全场景概率模型

为实现多随机参数(DG出力、负荷等)的并行场景划分，提出一种基于离散Bayes公式的全场景概率建模方法。设配电网中多DG组合的场景离散分布为{S1，S2，…，Si，…SN}，对应的场景离散分布概率为{P1*，P2*，…，Pi*，…，PN*}；负荷场景的离散分布为{L1，L2，…，Lj，…LM}，对应的场景概率为{Pload(L1)，Pload(L2)，…，Pload(Lj)，…，Pload(LM)}，其中M为负荷场景数，Pload()为对应的负荷场景概率。将运行参数的动态随机变化用基于场景划分的DG出力和负荷离散分布的确定的组合状态代替，组合状态的2个因素具有部分相关性，其离散概率由Bayes公式求得。由概率论知识，事件S1，S2，…，Si，…SN构成一个完备事件组，L∈{L1，L2，…，Lj，…LM}，对于每个Sk有:

(12)

(13)

式中：P(Sk|L)和P(L|Sk)分别为事件L发生的情况下事件Sk发生的条件概率，以及事件Sk发生的情况下事件L发生的条件概率；P(SkL)为事件Sk和事件L同时发生的概率。

2 多随机参数下的配电网无功优化模型

2.1 目标函数

以有功损耗和电压偏移量最小为目标函数，建立基于多随机参数下的配电网无功优化模型：

(14)

(15)

式中：f1、f2分别为有功损耗和电压偏差；Ui、Uj分别为节点i和j的电压值；Gij、Bij和θij为节点i、j的互电导、互电纳和相位差；NL、Bi为系统节点总数和节点i的邻近节点集合；Uimax、Uimin分别为节点i的电压的上下限。

2.2 约束条件

(16)

(17)

(18)

式中：式(16)为潮流平衡方程，Pi、Qi为节点i的注入有功和无功；N为系统总节点数；式(17)为控制变量约束方程，Cimax、Cimin分别为电容器的无功容量最大值、最小值；QDGimax、QDGimin分别为配网中DG无功出力的最大值、最小值；KTmax、KTmin分别为有载调压变压器的分接头的上、下限值；NC、NDG分别为电容器数目和配电网中的DG数量；式(18)为状态变量约束条件，Uimax、Uimin分别为节点i电压的上限和下限。

3 算例分析

采用如图2所示的IEEE 33配电网节点系统[11]，检验所提算法的有效性。节点33、13分别接入DG1和DG2，其额定容量为1 MW和0.5 MW；节点6和31处各安装5组并联无功补偿电容器，每组50 kvar。风力发电机组的有功和无功输出曲线[2]和负荷数据[4]进行归一化处理，基准值取负荷最大容量值，电压允许偏差为-5%～+5%。采用MOEA/D算法求解上述多目标无功优化问题具体见文献[14-15]，其参数设置为：种群数目为25，最大进化代数为50，变异因子为0.6～0.9。为简化计算，假设DG的有功输出为其当前出力上限，DG无功输出在一定范围内可控和负荷功率因素恒定；枢轴量法的检验水平α取0.05，置信度取1-α，方差值σ2取置信区间中点值。

图2 IEEE 33配电系统接线图Fig.2 Wiring diagram of IEEE distribution system

改进后的测试系统中随机参数主要有DG出力和负荷，由公式7可计算出全场景数为63，运用公式12、13可得各场景出现的概率，部分场景中DG有功百分数PDG、负荷百分数PL和场景概率P如表1所示。

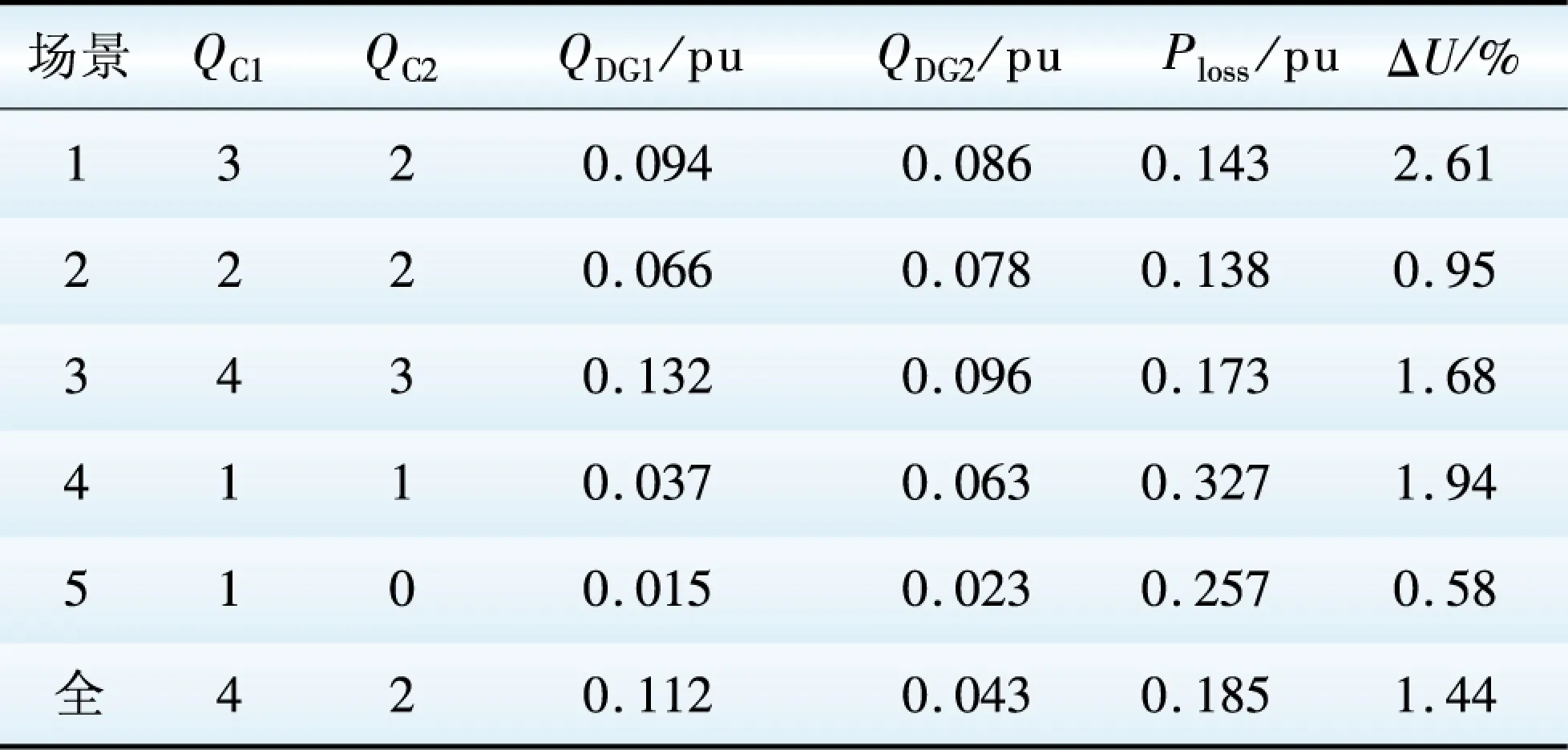
部分优化结果如表2所示，全场景网损Ploss、电压偏移ΔU%、DG无功出力QDG和电容器投切组数QC为各自对应的期望值。此外，场景1和场景2的DG出力相同负荷不同，场景3和场景4的DG出力不同负荷相同。优化前场景4的网损大于场景3，电压偏移则相反；优化后网损与电压偏移均有所改善，场景2的目标函数值均优于场景1，场景4的目标函数值均优于场景3，由此说明了计入多随机参数变化及DG并网后无功优化的必要性。

表1 部分典型场景的主要参数

Table 1 Main parameters of part typical scenes

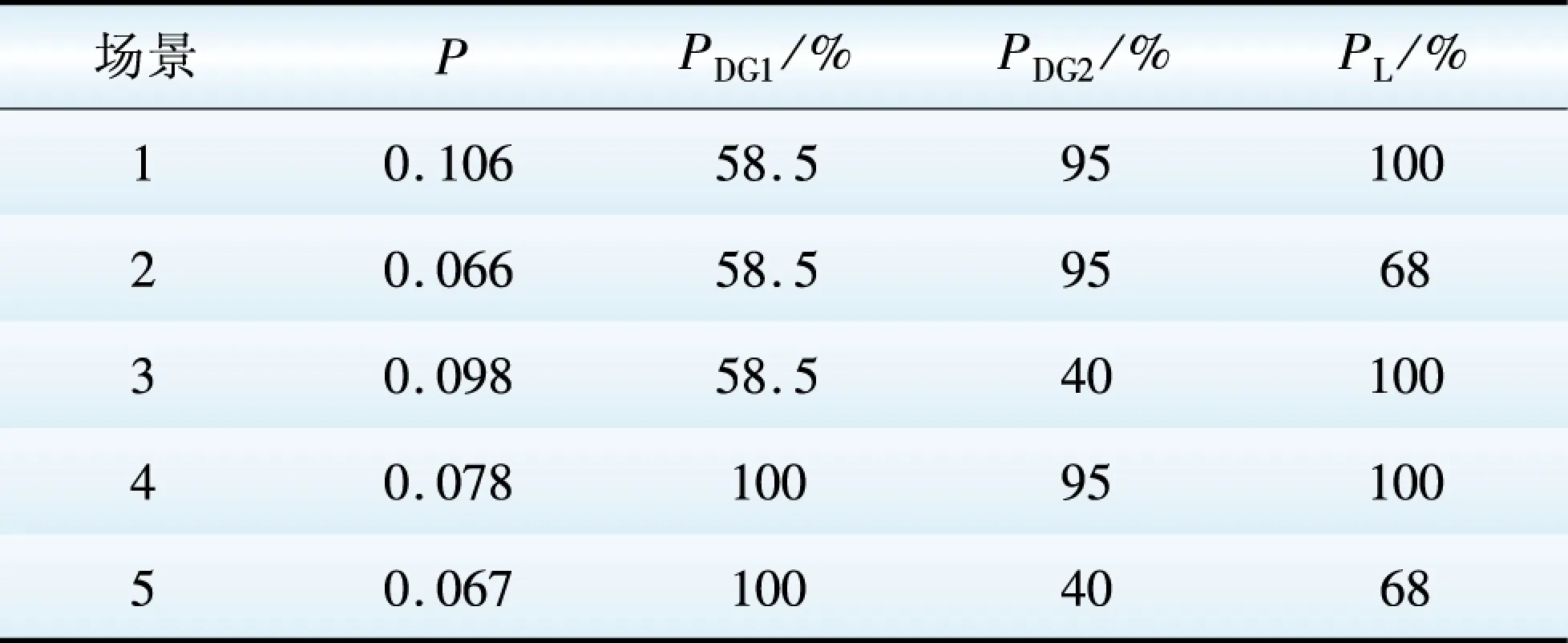
表2 部分无功优化结果Table 2 Part of reactive power optimization results

如图3所示，s1和s2分别是将典型场景1与全场景的优化方案分别应用于所有场景，画出的节点6电压概率密度曲线，其中纵坐标为对应电压值出现概率，横坐标为电压值。由图可知，s1曲线电压值存在电压偏移越下限的现象，而s2曲线电压值并不越上下限，因此，单个典型场景的确定性无功优化结果不能代表全局最优解，全场景优化结果虽不是各典型场景的最优解，但不存在电压越上下界的情况，同时说明了本文基于全场景优化的概率模型很好地模拟了多随机参数变化的特性，优化方案具有全场景下的普适性。

图3 2种方案下节点6的电压概率密度Fig.3 Probability density of bus-6 voltage in two schemes

为验证基于Bayes公式所构建的场景概率模型对真实情况的模拟性能，与多种随机无功优化建模方法进行了对比，主要有仿真法中的蒙特卡罗法(Monte Carlo simulation)；解析法中的点估计法(point estimation method，PEM)和基于Gram Charlier级数和半不变量的概率潮流法；上述仿真法和解析法的建模方法细节可参考相关文献[16-18]。对以上各个无功优化模型分别重复测试20次，统计出各模型所得优化目标均值，测试结果如表3所示，其中网损和电压偏移为期望值。

表3 多种建模方式下的无功优化性能对比

Table 3 Performance comparison of reactive power optimization in various modeling methods

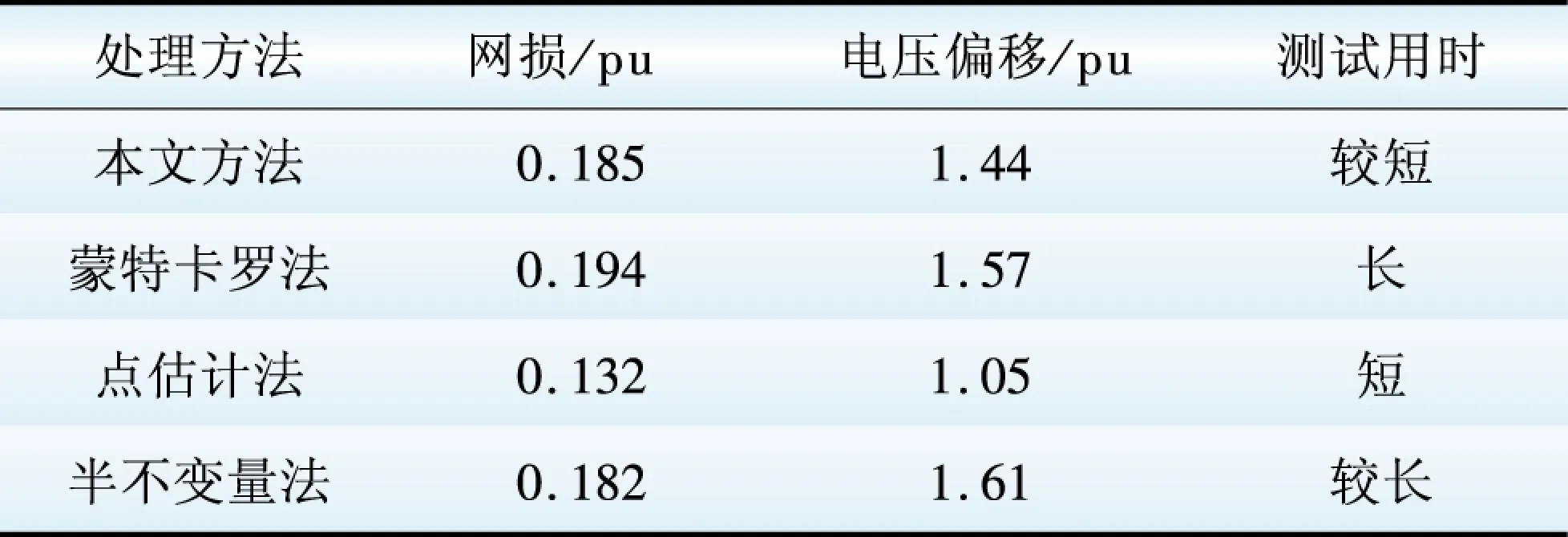
从多次测试得出的优化结果的均值来看，4种模型下的优化结果差距在一定范围内，说明了这4种方法在一定程度上均能够解决多随机参数动态变化下的配电网无功优化问题。此外，本文方法与蒙特卡罗法所得结果最为接近，测试用时介于半不变量法与点估计法之间。由此可见本文方法具有较好的鲁棒性和精确性，能很好地模拟配电网运行参数随机变化特性，其优化精度与蒙特卡罗模型接近，用时却大幅减少，但仍具有巨大的发展空间。

4 结 论

采用基于枢轴量法所建的负荷概率模型具有较强的鲁棒性和实用性，该模型既实现了实际负荷模型的理想化，又真实地反映了实际负荷的波动性。运用Bayes公式改进的场景分析法解决了多随机参数并行时的场景概率计算问题，进而实现了多维时间和空间的解耦，将本文方法与其他不确定随机参数处理方法做比较，验证了本文方法优化结果较为精确，所用时间也较短。

[1]Cheng S， Chen M Y. Multi-objective reactive power optimization strategy for distribution system with penetration of distributed generation[J]. International Journal of Electrical Power & Energy Systems， 2014， 62： 221-228.

[2]Kolenc M， Papic I， Blazic B. Coordinated reactive power control to achieve minimal operating costs[J]. International Journal of Electrical Power & Energy Systems， 2014， 63： 1000-1007.

[3]李剑辉， 曹阳， 辛拓， 等. 考虑电压暂降风险的高压配网动态无功容量优化配置[J]. 电力系统保护与控制， 2014， 42(8)： 47-53. Li Jianhui， Cao Yang， Xin Tuo， et al. Study on high voltage distribution network dynamic optimal allocation of reactive power capacity considering the risk of voltage sag[J].Relay， 2014， 42(8)：47-53.

[4]叶承晋， 黄民翔， 王焱， 等. 基于离散概率模型的风光互补供电系统优化配置[J]. 电力系统自动化， 2013， 37(6)： 48-54. Ye Chengjin， Huang Minxiang， Wang Yan， et al. A hybrid wind/photovoltaic power supply system based on discrete probabilistic methodology[J].Automation of Electric Power Systems，2013，37(6)：48-54.

[5]张沈习， 程浩忠， 张立波， 等. 含风电机组的配电网多目标无功规划[J]. 电力系统保护与控制， 2013， 41(1)： 40-46. Zhang Shenxi， Cheng Haozhong， Zhang Libo， et al. Multi-objective reactive power planning in distribution system incorporating with wind turbine generation[J]. Power System Protection and Control， 2013， 41(1)： 40-46.

[6]于青， 韩学山， 杨思， 等. 计及风电的动态无功优化解耦算法[J]. 中国电力， 2013， 46(11)： 52-56. Yu Qing， Han Xueshan， Yang Si， et al. Decoupling algorithm of dynamic reactive power optimization with consideration of wind power [J]. Electric Power， 2013， 46(11)： 52-56.

[7]刘沛津， 谷立臣. 含风电场的电力系统无功规划优化[J]. 电网技术， 2010， 34(7)： 175-180. Liu Peijin， Gu Lichen. Optimization of reactive power planning for power system containing wind farms[J]. Power System Technology， 2010， 34(7)： 175-180.

[8]段建东， 杨杉. 基于改进差分进化法的含双馈型风电场的配电网无功优化[J]. 电力自动化设备， 2013， 33(11)： 123-127. Duan Jiandong， Yang Shan. Reactive power optimization based on modified differential evolution algorithm for power distribution system with DFIG wind farms[J].Electric Power Automation Equipment， 2013， 33(11)： 123-127.

[9]赵晶晶， 符杨， 李东东. 考虑双馈电机风电场无功调节能力的配电网无功优化[J]. 电力系统自动化， 2011， 35(11)： 33-38. Zhao Jingjing， Fu Yang， Li Dongdong. Reactive power optimization in distribution network considering reactive power regulation capability of DFIG wind farm[J]. Automation of Electric Power Systems， 2011， 35(11)：33-38.

[10]何禹清， 彭建春， 毛丽林， 等. 含多个风电机组的配电网无功优化[J]. 电力系统自动化， 2010， 34(19)： 37-41. He Yuqing， Peng Jianchun， Mao Lilin， et al. Reactive power optimization in distribution system with multiple wind power generators[J].Automation of Electric Power Systems， 2010， 34(19)： 37-41.

[11]程杉. 含分布式电源的配电网多目标优化问题研究[D]. 重庆：重庆大学， 2013. Cheng Shan. Study on multi-objective optimization of distribution network with distributed generation[D]. Chongqing： Chongqing University， 2013.

[12]陈璨， 吴文传， 张伯明， 等. 基于多场景技术的有源配电网可靠性评估[J]. 中国电机工程学报， 2012， 32(34)： 67-73. Chen Can， Wu Wenchuan， Zhang Boming， et al. An active distribution system reliability evaluation method based on multiple scenarios technique[J].Proceedings of the CSEE， 2012， 32(34)： 67-73，11.

[13]陈魁. 应用概率统计[M]. 北京： 清华大学出版社，2000.

[14]Carvalho R， Saldanha R R， Gomes B N， et al. A multi-objective evolutionary algorithm based on decomposition for optimal design of Yagi-Uda antennas[J]. IEEE Transactions on Magnetics， 2012， 48(2)： 803-806.

[15]刘海林， 辜方清， 张晓明. 基于幂变换的多目标进化算法 MOEA/D 权重设计方法[J]. 计算机研究与发展， 2012， 49(6)： 1264-1271. Liu Hailin， Gu Fangqing， Cheung Yiuming. A weight design method based on power transformation for multi-objective evolutionary algorithm MOEA/D[J].Journal of Computer Research and Development，2012， 49(6)： 1264-1271.

[16]郭金明. 基于2层规划的间歇性分布式电源和无功补偿优化配置[D]. 长沙： 湖南大学， 2013. Guo Jinming. Optimal allocation of intermittent distributed generation and reacitive power compensation based on bilevel programming[D]. Changsha：Hunan University， 2013.

[17]罗钢， 石东源， 蔡德福， 等. 计及相关性的含风电场电力系统概率可用输电能力快速计算[J]. 中国电机工程学报， 2014， 34(7)： 1024-1032. Luo Gang， Shi Dongyuan， Cai Defu， et al. Fast calculation of probabilistic available transfer capability considering correlation in wind power integrated systems[J]. Proceedings of the CSEE， 2014， 34(7)： 1024-1032[18]芦晶晶， 赵渊， 赵勇帅， 等. 含分布式电源配电网可靠性评估的点估计法[J]. 电网技术， 2013， 37(8)： 2250-2257. Lu Jingjing， Zhao Yuan， Zhao Yongshuai， et al. A point estimation method for reliability evaluation of distribution network with distributed generation[J].Power System Technology，2013(8)：2250-2257.

(编辑：刘文莹)

Multi-Objective Reactive Power Optimization with Multiple-Random Parameters for Distribution Network

ZHANG Hang1， DING Xiaoqun1， HE Jian2， DENG Jixiang1

(1.College of Energy and Electrical Engineering，Hohai University， Nanjing 211100， China;2. Maintenance Company, State Grid Hebei Electric Power Company, Shijiazhuang 050070, China)

In the light of the problem that chronological load model could not be directly used in reactive power optimization, a new load modeling method was proposed based on the pivotal quantity. Because the multiple random parameters in distribution network were in parallel, a temporal and spatial decoupling scenario partition strategy was proposed based on the Bayes formula, and then the multi-objective reactive power optimization model was established with multiple random parameters for distribution network. At last, the improved IEEE33 standard node test system was used to verify the effectiveness of the proposed model, and the results proved that this method was efficient and flexible.

distribution network; multiple-random parameters; Bayes formula; pivotal quantity

TM 71

A

1000-7229(2015)06-0065-05

10.3969/j.issn.1000-7229.2015.06.011

2014-12-25

2015-04-30

张杭(1991)，男，硕士研究生，主要从事电力系统运行与控制方面的研究工作；

丁晓群(1956)，男，教授，博导，主要从事变压器故障诊断、电力系统运行与控制等方面的研究工作；

何健(1987)，男，硕士研究生，主要从事电力系统运行与控制方面的研究工作；

邓吉祥(1991)，男，硕士研究生，主要从事电力系统运行与控制方面的研究工作。