短波频段输电线路无源干扰谐振影响因子的关联性分析

陈彬，唐波，曹红英，彭友仙，李昱

(三峡大学电气与新能源学院，湖北省宜昌市 443002)



短波频段输电线路无源干扰谐振影响因子的关联性分析

陈彬，唐波，曹红英，彭友仙，李昱

(三峡大学电气与新能源学院，湖北省宜昌市 443002)

IEEE对中波频段输电线路无源干扰谐振机理及其影响因子进行了较为深入的研究，但相关结论无法解释短波频段无源干扰仍存在的谐振现象。为得到短波频段输电线路无源干扰谐振的决定性影响因子，考虑各种可能对干扰造成影响的因素，如线路档距、铁塔数量、导线、地线等单一宏观结构，研究输电线路与天线组成的电磁开放系统中场域的无源干扰水平。引入灰色系统理论及相关性分析，计算各种影响因子对干扰变化的灵敏度，得到各种宏观结构与干扰的关联程度。分析结果表明，线路档距是短波频段无源干扰谐振的决定性影响因子，线路设计阶段可采取调整档距的方法规避干扰极值频点。

输电线路；无源干扰谐振；灰色系统理论；相关性分析；影响因子

0 引 言

随着我国特高压电网的建设，特高压输电线路对邻近的电力电子和弱电系统(包括调幅广播台站、短波无线电测向和收信台站、电视差转和转播台、中波航空无线电导航台站、对海中远程无线电导航台、对空情报雷达站、无线基站、地震台和卫星地球站等)的无源干扰问题越显突出[1]。因此，特高压输电线路无源干扰的谐振机理研究及干扰防护工作已经成为当前电力系统电磁兼容领域的重要内容。

IEEE对中波频段输电线路无源干扰谐振机理及其影响因子进行了较为深入的研究，认为避免出现无源干扰谐振现象是干扰防护的最根本方法。无源干扰防护技术主要基于铁塔和地线相互绝缘，中断回路以减小线路上的感应电流，从而破坏谐振发生的条件。基于铁塔和地线相互绝缘的思想，IEEE设计了多种“解谐器”[2]。另外，C.W. Trueman和S.J. Kubina提出了宏观上对整条线路的环路按一定规律“解环”的办法[3]。但以上这些研究频率均集中在中波频段。

为探寻短波频段输电线路无源干扰谐振的决定性影响因子及其干扰防护技术，文献[4]对感应电流幅值与无源干扰的变化规律进行研究，发现短波频段感应电流与无源干扰水平不在对应，而且随着频率的增加，这种差异越来越明显，说明干扰谐振的决定性影响因子不再是地线感应电流。在后续的研究中发现，在1.705 MHz以上的频段内，输电线路无源干扰仍具有谐振的特征且存在周期性振荡现象，其干扰幅值呈递增趋势，其干扰谐振机理与中波谐振机理可能有所不同[5]。

为了明确短波频段线路无源干扰谐振机理及决定性影响因子，本文采用与文献[2]类似的方法，从线路各种宏观结构变量与干扰变化的关联性出发，引入考虑系统内在因素之间相互影响程度的灰色系统理论和相关性分析等分析方法，研究各种可能对输电线路无源干扰造成影响的因素，如线路档距、铁塔数量、导线、地线等单一宏观结构与干扰变化的关联度和相关系数，进而得到短波频段线路干扰谐振的决定性影响因子，以此为未来短波频率无源干扰防护技术手段的研究提供指导和参考。

1 无源干扰谐振的影响因子

1.1 IEEE提出的中波频段干扰谐振影响因子

IEEE基于“环形天线”理论，并结合文献[2，3]的研究结果，解释了铁塔与地线相连情况下，在宏观结构方面，影响调幅广播频段(0.535～1.705 MHz)的无源干扰谐振因子为铁塔和地线对地镜像所组成的“环形天线”周长[6]。为进一步揭示中波频段谐振的内在机理，根据1.7 MHz以下频率的无源干扰水平和地线感应电流幅值曲线的变化规律近似相同，以及谐振频率点处地线感应电流沿“环形天线”呈驻波分布的特点，提出感应电流是干扰谐振的决定性因子[5]。这两者并不冲突，前者的侧重点是线路的宏观结构，后者更加偏于内在谐振机理的研究。

同时，IEEE基于“半波天线”原理，结合文献[7]的研究结果，阐述了铁塔与地线未相连情况下，在宏观结构方面，影响调幅广播频段的干扰谐振因子为铁塔高度。当铁塔与地线通过避雷器相连时，若将交变电磁场中的铁塔视为垂直于地面的线天线，则可根据“半波天线”理论，认为铁塔高度达到λ/4时会产生干扰谐振。考虑到铁塔横担的影响，认为铁塔电气高度比实际塔高增加了15%[5]。

1.2 短波频段干扰谐振影响因子的研究进展

由于IEEE提出的铁塔线模型过于粗略，无法用于调幅广播以上频段的干扰求解。随着研究的深入，文献[8]提出了适用于短波频段的输电线路线-面混合模型。文献[4]采用线-面混合模型对±800kV特高压直流输电线路对调幅广播一级收音台(频率0.536 5～26.1MHz)防护间距进行研究，发现对于1.7MHz以上频段，输电线路无源干扰仍具有谐振的特征且存在周期性振荡现象，其干扰幅值呈递增趋势。

目前，可以查阅到一些有关短波频段输电线路无源干扰谐振机理的文献[4，6，8-9]，研究结论表明短波频段干扰谐振的内在机理不再是感应电流，且干扰谐振与电磁开放系统所具有的铁塔数量、档距等宏观结构密切相关，但以上研究均未从定量的角度明确干扰决定性影响因子。

2 谐振影响因子的关联性分析方法

2.1 灰色关联分析法

2.1.1 干扰谐振影响因子的确定

灰色关联度的基本思想是根据序列曲线几何形状的相似程度来判断其内在联系是否紧密，可以定量描述因素之间相互变化的情况。如果因素的变化态势基本一致，则可以认为其间的关联度较大，反之，关联度较小[10-11]。

输电线路无源干扰现象产生的根本原因是无线电波受到铁塔、导线等金属部件宏观结构的影响。因此，选择线路档距、铁塔数量、导线、地线等反映输电线路宏观结构的因素作为可能的干扰谐振影响因子。

假定存在I+1个影响因子，求解各种影响因子情况下的短波频段无源干扰水平。若在短波频段等间隔选择J个频点，则第i种影响因子对应的数据列为{xi(j)，i=0，1，2，…，I;j=1，2，…，J}。为了衡量各种宏观结构对干扰谐振的影响程度，选择一组数据列{x0(j)，j=1，2，…，J}作为被参考序列，其余列作为参考序列。

2.1.2 各频点影响因子关联系数的计算

确定短波频段干扰决定性影响因子，相当于从多种变量中选择出对干扰曲线的变化幅值、方向和速度等信息影响最为显著的宏观结构。从几何的角度，可采用曲线间的差值大小作为关联度的衡量标准，即

(1)

式中Δi(j)表示第j个频点处第i种参考影响因子与被参考影响因子的干扰水平偏差值。

短波范围内各种参考影响因子与被参考影响因子间最大偏差值与最小偏差值为

(2)

(3)

第j个频点处第i种参考影响因子与被参考影响因子的关联系数为

(4)

式中ρ为分辨系数，用来削弱Δ(max)过大而导致的关联系数失真的影响，提高关联系数之间的差异显著性，ρ∈(0，1)。

2.1.3 各种影响因子关联度的计算

每个参考影响因子与被参考影响因子间的关联程度是通过J个关联系数来反应的，关联信息分散，不便于从整体上进行比较。因此，有必要对关联信息作集中处理。求平均值便是一种信息集中的方式，即用各频点参考影响因子与被参考影响因子的关联系数平均值来定量反应这2个数列的关联程度，其计算公式为

(5)

式中γ0i表示第i种参考影响因子与被参考影响因子之间的关联程度。

若某参考影响因子对应的γ0i越大，说明该宏观结构变化并未对干扰造成显著影响，即该宏观结构不是短波频段干扰水平的决定性影响因子；反之，关联程度越小，说明该宏观结构对干扰造成显著影响，即该宏观结构为干扰的决定性影响因子。

2.2 相关分析法

相关系数是变量之间相关程度的指标。引入相关性系数，可以分析单一宏观结构对应的参考序列与被参考序列的相关性强弱。相关性越强，说明该宏观结构变化对干扰的影响不明显，即该宏观结构并非短波频段干扰水平的决定性影响因子；反之，相关性越弱，说明该宏观结构为短波频段干扰水平的决定性影响因子[12]。

第i个参考影响因子和被参考影响因子之间的相关系数计算表达式为

(6)

3 短波频段无源干扰的关联性分析

3.1 模型的建立

由于研究的频率范围为短波频段(3～30 MHz)，因此，需要采用文献[8]研究用输电线路无源干扰线-面混合模型。以800kV向家坝—上海特高压直流输电线路ZP30101型铁塔为例，铁塔高63 m，横担宽42.2 m。导线采用6×ACSR-720/50钢芯铝绞线，导线外径为36.24 mm，分裂间隔为450 mm。根据DL/T 691-19《高压架空送电线路无线电干扰计算方法》[13]，对分裂导线用半径0.355 1 m的单根等效导线代替。铁塔与双地线连接，地线型号LBGJ-180-20AC，该型地线直径为17.5 mm，两根地线相距32.4 m，弧垂13 m。上述输电线路的线-面混合模型如图1所示。

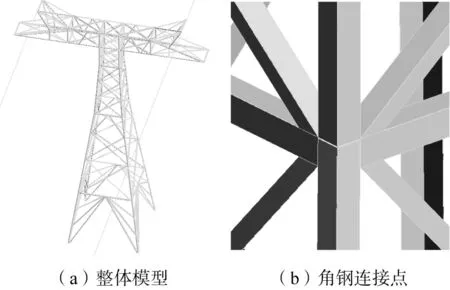
图1 特高压直流无源干扰ZP30101型铁塔线-面模型Fig.1 Wire-surface model of ZP30101 tower of passive interference from UHVDC

由于各类无线台站电磁波发射天线的种类、大小和型号均不同，造成输电线路的无源干扰影响程度也不同，不能用具体的台站天线对仿真模型进行激励。因此，只能假设各类无线台站在无穷远处入射平面电磁波对输电线路模型进行激励。由于线路铁塔垂直于地面，考虑最严重的情况，即用垂直极化平面波为激励源。激励电场强度为1 V/m，选取观测点(0，2000，2)的无源干扰水平作为研究对象[13]。输电线路与观测点相关位置如图2所示。

图2 输电线路与观测点相关位置布置图Fig.2 Location of transmission line and observation point

当单一宏观结构变化时，可能导致系统内其余结构的改变。例如，当系统保持5基铁塔，线路档距按照300、500、700 m改变时，研究系统的输电线路总长度将随之按照1 500、2 500、3 500 m发生变化，此时线路档距和线路总长度等2种系统宏观结构均发生改变。为了保持系统变化量的唯一性，避免线路总长度对无源干扰产生影响，在输电线路两端接匹配电阻(377 Ω)模拟无限长线路。

针对上述开放系统中输电线路线-面模型对应的电场积分方程，遵循矩量法的求解步骤，利用脉冲基函数、RWG基函数和线-面连接点基函数对其进行离散，进而得到矩阵方程，最终求解得到场点的无源干扰水平[8]。

3.2 不同影响因子下无源干扰水平的求解

目前特高压输电线路无源干扰研究中，均用5基铁塔来表示整条输电线路，且线路档距选择代表档距500 m。因此，选择k=2，d=500 m时观测点无源干扰水平作为被参考序列。对图1所示仿真模型按照0.1倍的波长进行分段，激励电磁波的频率间隔为0.1 MHz，即被参考序列共270个元素，采用矩量法对短波各频率点的无源干扰进行扫频计算，得到被参考序列{x0(j)，j=1，2，…，270}。

3.2.1 铁塔数量对无源干扰水平的影响

为研究铁塔数量对无源干扰谐振特性的影响规律，控制档距、地线等因素不变，保持矩量法求解过程中网格划分、频率间隔、观测点等与被参考序列的计算过程一致，分别计算短波频段3基和7基铁塔组成的输电线路的无源干扰水平，即k=1，d=500 m和k=3，d=500 m时，对应的参考序列x1(j)和x2(j)，计算结果如图3所示。

图3 铁塔数目对无源干扰的影响Fig.3 Impact of tower number on passive interference

3.2.2 档距对无源干扰水平的影响

为研究档距对无源干扰谐振特性的影响规律，控制铁塔数量、地线等因素不变，保持矩量法求解过程中网格划分、频率间隔、观测点等与被参考序列的计算过程一致，分别计算短波频段输电线路档距300、700 m的无源干扰水平，即k=2，d=300 m和k=2，d=700 m时，对应的参考序列x3(j)和x4(j)，计算结果如图4所示。

图4 档距对无源干扰的影响Fig.4 Impact of spans on passive interference

3.2.3 导线对无源干扰水平的影响

为研究导线对无源干扰谐振特性的影响规律，控制档距、铁塔数量、地线等因素不变，保持矩量法求解过程中网格划分、频率间隔、观测点等与被参考序列的计算过程一致，分别计算短波频段输电线路有弧垂导线、水平导线2种模型的无源干扰水平，对应的参考序列x5(j)和x6(j)，计算结果如图5所示。

图5 导线对无源干扰的影响Fig.5 Impact of conductor on passive interference

3.2.4 地线对无源干扰水平的影响

为研究地线对无源干扰谐振特性的影响规律，控制档距、铁塔数量、导线等因素不变，保持矩量法求解过程中网格划分、频率间隔、观测点等与被参考序列的计算过程一致，分别计算短波频段输电线路无地线模型的无源干扰水平，对应的参考序列为x7(j)，计算结果如图6所示。

3.3 关联度和相关系数的求解

根据矩量法得到的被参考序列和7个参考序列，将各序列进行归一化处理，并分别计算7个参考序列与被参考序列之间各个频点的关联系数，最后通过均值化的集中处理方式得到各参考序列与被参考序列的灰色关联度。同样，按照上述步骤，分别计算7个参考序列与被参考序列之间的相关系数。这2种方法的计算结果如表1所示。

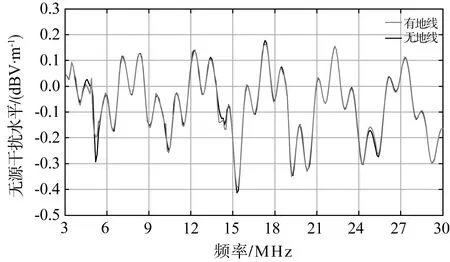
图6 地线对无源干扰的影响Fig.6 Impact of grounding wire on passive interference

表1 灰色关联度和相关系数的计算结果

Table 1 Calculation results of grey incidence and correlation coefficient

3.4 结果分析

(1)由表1可知，参考序列与被参考序列间的关联度为γ05≈γ06≈γ07>γ01≈γ02>γ03>γ04；相关系数的计算结果为r5=r6≈r7>r1≈r2≫r4>r3。从总体上来说，这2种方法均能反映：档距变化对应的参考序列与被参考数列相关性较弱，而铁塔数量、弧垂导线、水平导线和无地线等情况对应的参考序列与被参考数列相关性较强。这2种方法得出的结论是一致的，原因分析如下：

在各种宏观结构的关联度计算公式(5)中，Δ(min)、ρ、Δ(max)均为定值，即公式(5)可改写为

(7)

由此可见，γ0i与Δi(j)相关，Δi(j)表示相同频点处参考曲线与被参考曲线间的差值或距离，距离越小，关联度γ0i越大。

在相关系数计算公式中，

(8)

式中∑[xa(j)-a-bxb(j)]2同样表示相同频点处两条曲线之间的距离，距离越小，相关系数rb越大。

由此可见，尽管两者的定义不同，但本质上都取决于相同频点处两条曲线之间的距离，因此，两种方法在解决同一问题时，结论是一致的。

(2)关联度与相关系数存在一定的差异。从表1可知，γ03>γ04，而r4>r3。上述差异是由于关联度和相关系数的定义不同导致的结果，但这种差异不会影响整体结论。

(3)不存在地线的情况下，γ07≈r7且均接近1，表明在短波频段地线存在有否对无源干扰谐振特性没有影响，这一点与地线对中波频段谐振特性的影响规律有本质的区别；存在水平导线和13m弧垂导线情况下，对应的关联度和相关系数均接近1，说明导线的存在只是使输电线路无源干扰水平曲线产生微量变化。该结果与IEEE相关研究和实验结论一致。

4 结 论

(1)基于各种单一宏观结构对应的短波频段输电线路无源干扰曲线之间的关联度和相关性分析，可以有效地说明档距对短波频段无源干扰谐振现象的影响最为显著。即从宏观结构的角度出发，档距是短波频段内输电线路无源干扰谐振的决定性影响因子。

(2)为抑制输电线路对其周边已存在的各类短波无线电台站的无源干扰，在线路设计阶段就可从宏观上采取改变档距等线路宏观结构的措施，规避无源干扰极值频点出现在台站的工作频点或台站允许的带宽范围内。

[1]邬雄，万保权，张小武，等. 1 000kV特高压交流同塔双回线路对无线电台站影响及防护研究[R].武汉，湖北：国网武汉高压研究院，2008.

[2]TruemanCW，KubinaSJ，BelroseJS.CorrectivemeasuresforminimizingtheinteractionofpowerlineswithMFbroadcastantennas[J].IEEETransactiononElectromagneticCompatibility，1983，25(3)：329-339.

[3]TruemanCW，KubinaSJ.Detuningpowerlinesbyisolatingtowersforthesuppressionofresonances[J].IEEETransactiononBroadcasting，1986，32(3)：44-55.

[4]唐波，文远芳，张小武，等. 中短波段输电线路无源干扰防护间距求解的关键问题[J]. 中国电机工程学报，2011，31(19)：129-137.TangBo，WenYuanfang，ZhangXiaowu，etal.KeyproblemsofsolvingreradiationinterferenceprotectingdistancebetweenpowertransmissionlineandradiostationatMFandSF[J].ProceedingsoftheCSEE，2011， 31(19)： 129-137.

[5]TangBo，ZhaoZhibin，ZhangJianggong，etal.AdvancesinresearchesofthereradiationinterferencefromUHVpowerlines[J].HighVoltageEngineering，2013，39(10)：2372-2383.

[6]IEEEStandard1260—1996.IEEEguideontheprediction，measurement，andanalysisofAMbroadcastreradiationbypowerlines[S].NewYork：IEEE，Inc.， 1996.

[7]唐波，陈彬，赵志斌，等. 基于模型参数估计技术的输电线路散射特性快速求解[J]. 中国电机工程学报，2015， 35(5)： 1273-1280.TangBo，ChenBin，ZhaoZhibin，etal.Fastcalculationforcharacteristicofpowertransmissionlinebasedonmodel-basedparameterestimationtechnique[J].ProceedingsoftheCSEE， 2015， 35(5)： 1273-1280.

[8]唐波，葛光祖，张建功，等. 特高压直流线路对调幅广播台无源干扰防护间距的求解[J]. 信阳师范学院学报，2013，26(4)： 577-580.TangBo，GeGuangzu，ZhangJiangong，etal.ProtectingdistanceofreradiationinterferencebetweenUHVDCpowerlineandreceivingstationofAMbroadcasting[J].JournalofXinyangNormalUniversity， 2013， 26(4)： 577-580.

[9]郝阳，贺立斋，张建华，etal. 变电站铜塔双进出线电磁环境分析[J]. 电力建设， 2011， 32 (10)： 23-26.HaoYang，HeLizhai，ZhangJianhua，etal.Analysisontheelectromagneticenvironmentunderdouble-circuitinsubstation[J].ElectricPowerConstruction， 2011， 32 (10)： 23-26.

[10]汤少梁，李南，巩在武. 灰色绝对关联度组合预测模型的性质研究[J]. 系统工程与电子技术，2008，30(1)： 89-92.TangShaoliang，LiNan，GongZhaiwu.Researchonpropertiesofcombinationforecastingmodelbasedonabsoluteofgreyincidence[J].SystemsEngineeringandElectronic， 2008， 30(1)： 89-92.

[11]邓聚龙. 灰理论基础[M]. 武汉：华中科技大学出版社，2002：122-209.

[12]何萍，林成科，李宏波. 云贵高原蒙自城市热岛效应分析[J]. 信阳师范学院学报， 2010， 23(2)： 260-264.HePing，LinChengke，LiHongbo.TheanalyseofurbanheatislandeffectinMengziofYunnanplateau[J].JournalofXinyangNormalUniversity， 2010， 23(2)： 260-264.

[13]国家电力公司.DL/T691—19 高压架空送电线路无线电干扰计算方法[S].北京：中国标准出版社，1999.

(编辑：蒋毅恒)

Association Analysis of Passive Interference Resonance Impact Factors for Transmission Lines at Short-Wave Frequency

CHEN Bin， TANG Bo， CAO Hongying， PENG Youxian， LI Yu

(College of Electronic Engineering & New Energy, China Three Gorges University,Yichang 443002, Hubei Province, China)

IEEE gives deeper research on the resonance mechanism and impact factors of passive interference resonance (PIR) for transmission lines at medium-wave frequency. However, the resonance phenomenon existing at short-wave frequency (SF) can’t be explained by above research conclusions. In order to research the decisive impact factors of PIR for transmission lines at SF, the possible impact factors of interference resonance, such as tower spans, tower number, conductor, grounding wire and other single macro structure were considered, and the passive interference level in the electromagnetic open system composed of transmission line and antenna was studied. Grey system theory and correlation analysis were introduced to calculate the sensitivity of impact factors to interference change, and the correlation degree of various macro structure and interference was obtained. The results show that the decisive impact factor of PIR at SF is tower spans, which can be adjusted to evade the resonance frequencies at line design stage.

transmission line; passive interference resonance; grey system theory; correlation analysis; impact factor

国家自然科学基金项目(51307098)；三峡大学研究生科研创新基金(2015CX037)。

TM 723

A

1000-7229(2015)06-0053-06

10.3969/j.issn.1000-7229.2015.06.009

2015-04-07

2015-05-06

陈彬(1989)，男，硕士研究生，主要从事先进输电技术及电力系统电磁兼容方面的研究工作；

唐波(1978)，男，博士，副教授，主要从事输变电系统电磁环境及超特高压输电技术方面的研究工作；

曹红英(1990)，女，硕士研究生，主要从事输电线路电磁兼容方面的研究工作；

彭友仙(1991)，女，硕士研究生，主要从事输电线路防雷及其电磁环境方面的研究工作；

李昱(1988)，男，硕士研究生，主要从事分布式发电及并网方面的研究工作。

Project Supported by National Natural Science Foundation of China (51307098).