机抖式激光惯组高动态下导航误差分析

尤太华 徐 帆 郭 康

北京航天自动控制研究所，北京100854

机抖式激光捷联惯组在惯性技术领域正日益受到重视，应用越来越广泛，对高精度导航的需求也日益强烈，但实际工程应用中经常面临以下现象与问题:1)飞行试验中大角速率、大过载机动时惯性导航误差急剧增大;2)六自由度振动导航精度试验中动态与静态条件下惯性导航精度差异大。

经分析，在机抖式捷联惯组应用中除了传统的圆锥与划桨效应引入的经典动态误差外，还存在由于激光捷联惯组结构以及陀螺机械抖动特性引入系统的新的、更为复杂的动态误差［1］。一方面陀螺抖动耦合以及抖动对加速度计的影响、加速度计与陀螺空间关系、结构谐振等使得系统输出除了载体真实运动外，还含有其他的干扰成分可能引入的动态误差;另一方面对于抖动偏频通常利用数字低通滤波器实现解调，但滤波器的特性不可避免的使通带内陀螺有效信号的幅频、相频特性发生变化，载体真实角运动频谱的畸变可能引入动态误差，以及减震器与滤波器不匹配，造成有效信号衰减引入动态误差。

针对上述动态误差，根据实际工程应用中的经验与分析，目前认知的动态误差因素包括:1)广义上的圆锥与划桨效应;2)加速度计尺寸效应;3)陀螺与加速度计动态响应特性影响。

1 广义上的圆锥与划桨效应

圆锥与划桨效应为传统意义上典型的动态误差，惯组受到再入环境振动或本身具有的角运动(如机械抖动)影响，其在2个正交轴方向存在一定同频角振动或线振动时，第3个正交轴在空间将绕其平均位置做锥面运动或出现速度整流量，称为圆锥和划桨效应。

1.1 经典圆锥与划桨效应分析

经典圆锥运动模型［2］如下式:

在此仅以惯性敏感轴Y和Z轴做周期性轴角振动，X轴做锥形运动为例。式中，α为锥半角，Ω为锥运动速率，经典圆锥运动也可以推广至两正交轴不同锥半角与锥频率的运动形式。

根据资料报道的典型激光陀螺参数:信号和频130kHz、抖幅 2.6'、基座抖幅 2.7″，3 个陀螺抖频分别为 354Hz，390Hz，422Hz，仿真计算可得等效陀螺漂移为 0.0026(°)/h。

在理论分析与应用中经典圆锥效应按下式可以进行补偿系数的推导［3］:

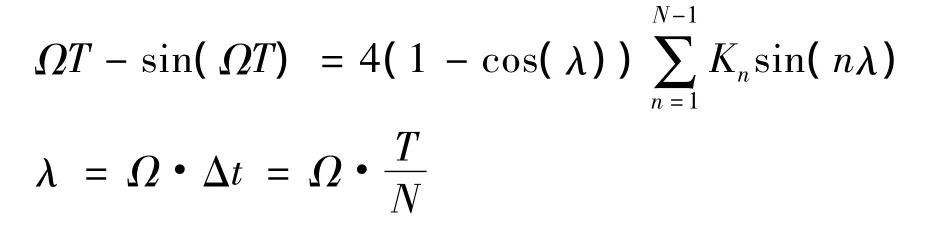
式中，T为圆锥补偿周期，N为子样数，公式两边按照泰勒展开即可计算圆锥效应补偿系数Kn，也可以根据需要扩展为单周期多子样或多周期多子样算法。

圆锥效应补偿计算则按下式［3］:

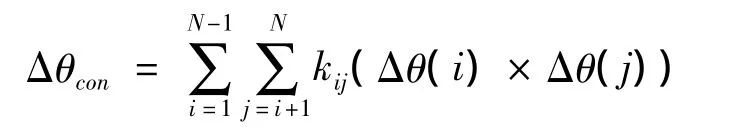
划桨效应与圆锥效应具有对偶性，因此划桨效应的分析、补偿计算与圆锥效应具有一致性，在此不再赘述。

1.2 广义圆锥与划桨效应分析

在实际工程应用中，由于采用数字低通滤波器进行陀螺解抖滤波处理，则陀螺信号经过滤波器后，圆锥运动模型如下式:

式中，Fω(Ω)为角运动速率为Ω时的幅度，Φω(Ω)为角运动速率为Ω时的相位。

根据分析，原始陀螺的比例因子稳定性由陀螺加工、调试工艺保证，经过低通滤波器后的陀螺比例因子相当于被滤波器的幅频特性所调制，因此在实际工程应用中解抖滤波会造成一定的陀螺比例因子误差，另外若按照经典圆锥效应系数进行补偿，可能会造成更大误差。

在工程中类似经典圆锥补偿系数推导，基于频域特性优化的圆锥补偿可以按下式［4］进行计算:

式中，T为圆锥补偿周期，N为子样数，Fω(Ω)为滤波器幅值函数。

由于经典圆锥效应的研究与分析比较深入，广义的基于频域特性优化的圆锥补偿与经典圆锥补偿类似，且补偿效果与采样周期、滤波器的特性等相关，本文限于篇幅不在此进行仿真计算的对比，但据分析可以得出如下结论:1)陀螺解抖滤波器由于通带内的幅频特性引入陀螺比例因子误差;2)机抖式激光惯组应根据采样频率、锥运动幅度、姿态更新算法选择是否进行圆锥效应补偿，若进行补偿则需根据滤波器的幅频特性进行优化，以减小圆锥补偿引入的误差;3)对于机抖式激光惯组，由于陀螺解抖滤波器带宽的限制，在进行圆锥补偿时需要考虑载体真实运动带宽的范围，以确保干扰造成的伪圆锥误差。

2 加速度计尺寸效应

在激光捷联惯组设计时，由于结构布局3个加速度计测量点不重合，在实际应用中，由于加速度计测量点不在测量坐标系原点，存在一定尺寸的杆臂，在陀螺抖动或大角速率机动导航计算时将产生干扰加速度，即加速度计的尺寸效应。

2.1 加速度计尺寸效应模型

2.2 加速度计尺寸效应仿真计算

在实际工程应用中，加速度计的尺寸效应参数，即内杆臂可以通过精确的理论结构设计参数给出，或者通过标定试验进行分离获取。但实际补偿时面临如下问题:激光捷联惯组采样输出为角度增量，角速度与角加速度需要进行微分计算，提取时的噪声较大，对尺寸效应补偿影响较大。

3 陀螺与加速度计动态响应特性影响

在理论分析时，激光捷联惯组通常将数字滤波器作为信号的低通滤波器［7］，在保证姿态控制幅相要求的同时，尽量达到一定的带宽、通带的增益稳定性、较小的延迟以及仪表间特性的一致性;减震器作

在此以某一飞行轨迹、某一惯组尺寸参数lbx=(0.05 0 0)T，lby=(0 0.05 0)T，lbz=(0 0 0.05)T(单位:m)进行仿真计算，以说明加速度计尺寸参数对导航的影响，惯性导航速度误差如图1所示。为运动的低通滤波器，使其通带范围与信号的滤波器通带一致，以消除滤波器通带之外的高频谐波振动。

图1 加速度计尺寸效应产生的导航速度偏差

3.1 陀螺与加速度计动态响应特性分析

惯组在系统设计时根据载体飞行剖面的力学环境，选取合适的减震器，在控制系统应用中重点关注陀螺与加速度计的动态响应特性。在满足姿态控制要求的基础上，导航计算中的误差主要包括:1)数字低通滤波器的带宽问题。若带宽不能覆盖载体真实运动的范围，则有效运动信息将被衰减，造成导航误差;2)数字低通滤波器通带内增益稳定性问题。增益稳定性直接表现为仪表的比例因子误差，若系统仪表比例因子稳定性要求为10ppm，则滤波器增益稳定性至少要优于1.0E-5;3)陀螺与加速度计动态响应特性的一致性问题。由于采用时域内离散采样与导航计算，当陀螺与加速度计动态特性不一致时，在有限转动条件下不可交换性使系统存在广义圆锥与划桨误差。

3.2 陀螺与加速度计动态响应特性的仿真计算

如图2～3所示，以某型激光惯组陀螺与加速度计的动态响应特性、某一飞行轨迹为例说明动态响应特性对导航的影响，仿真计算的速度偏差如图所示，图2表示该型激光惯组陀螺与加表的幅相特性，其中对导航的主要影响表现为陀螺相对加表相频的滞后，通带范围内平均群延迟约为5ms左右，图3表示在某一飞行轨迹条件下由于图2所示的陀螺与加表动态响应特性不一致，则造成一定的导航速度偏差。

因此，在工程应用中应根据实际情况选取合适的数字低通滤波器，保证一定的带宽与增益稳定性，并保证陀螺与加速度计具有一致的动态响应特性以减小动态误差。

图2 加速度计与陀螺动态响应特性图

图3 惯组动态特性产生的导航速度偏差

4 结论

随着机抖式激光捷联惯组应用越来越广泛，特别是在高动态条件下对导航精度要求也越来越高。以工程应用中的现象与问题为出发点，分析了高动态下广义圆锥与划桨效应、加速度计尺寸效应以及陀螺与加速度计动态响应特性对导航的影响，上述分析或有失偏颇，但针对工程应用中高动态下导航误差的探索与挖掘是有必要的，而且需要进一步深入研究，以提升机抖式激光捷联惯组的导航精度。

［1］ 王养柱.动态环境下捷联惯性导航系统设计与研究［D］.北京:北京航空航天大学，2001.(Wang Yang zhu.Design and Study on Strapdown Inertial Navigation System in Dynamic Environment［D］.Beijing:Beijing U-niversity of Aeronautics ＆ Astronautics，2001.)

［2］ 秦永元.惯性导航［M］.北京:科学出版社，2006.(Qin Yongyuan.Inertial Navigation［M］.Beijing:Beijing Science Press，2006.)

［3］ Ignagni M B.Duality of optimal strapdown sculling and coning compensition algorithms［J］.Journal of the Institute of Navigation，1998，45(2):85-95.

［4］ 潘献飞.基于机抖激光陀螺信号频域特性的SINS动态误差分析与补偿算法研究［D］.长沙:国防科技大学，2008.(Pan Xianfei.Research on the Dynamic Error and Compensation Algorithms of Dither RLG SINS Based on the Frequency Domain Characteristics［D］.Changsha:National University of Defense Technology，2008.)

［5］ 严恭敏，严卫生，徐德民.捷联惯性测量组件中内杆臂效应分析与补偿［J］.中国惯性技术学报，2008，16(2):148-153.(Yan Gongmin，Yan Weisheng，Xu Demin.Analysis and compensation on inner lever arm effect of strapdown inertional measurement unit［J］.Journal of Chinese Inertial Technology，2008，16(2).)

［6］ 吴文启，杨伟光，杨杰.激光陀螺捷联惯导系统尺寸效应参数标定与优化补偿［J］.中国惯性技术学报，2009，17(6):636-642.(Wu Wenqi，Yang Weiguang，Yang Jie.Calibration and optimal compensation for size effect parameters of laser gyro SINS［J］.Journal of Chinese Inertial Technology，2009，17(6):636-642.)

［7］ 杨伟光.捷联惯性导航系统动态误差标定与补偿算法研究［D］.长沙:国防科技大学，2009.(Yang Weiguang.Research on the Dynamic Error Calibration and Compensation Algorithms of SINS［D］.Changsha:National University of Defense Technology，2009.)