抗击高超音速巡航导弹地基雷达部署方法研究

刘 健 管维乐 刘志航

空军工程大学防空反导学院，西安710051

高超音速巡航导弹拥有极快打击速度、精准到达能力以及高速隐身突防能力，是快速全球反应作战的首选武器，必将引起未来作战样式的重大变革，使防空系统面临巨大挑战。

地基雷达是探测HCM的主要装备，因此，合理有效地部署地基雷达是抗击HCM的一个重要课题。关于地基雷达部署，国内外已有不少研究，但基本都是针对防空、反导的雷达部署方法［1-10］。由于HCM目标特性不同于以往空中目标和弹道目标特性，因此有必要对抗击HCM的雷达部署方法进行有针对性的研究。

HCM的作战距离可达数千公里，突击目标难以预测。因此，除了在HCM末段进行拦截以外，最好在其巡航飞行段进行多次拦截。所以，尽早预警、持续跟踪，提供目标信息，是抗击HCM的基本前提。

要使雷达尽早提供预警信息、稳定跟踪目标，就要求雷达有较大的探测距离和良好的跟踪能力。但是，雷达的探测、跟踪距离受多个因素的影响［11］，主要有:1)雷达自身的功率、增益和带宽等性能因素，限制了雷达的最大探测和跟踪距离;2)雷达探测跟踪能力还受到目标特性的影响，目标的速度和RCS、飞行姿态、机动能力等都会影响雷达的探测、跟踪距离;3)雷达探测距离还要受地球曲率、地物遮蔽和气候变化等环境因素的影响。目标特性、地物遮蔽和气候变化等因素引起雷达探测能力的变化，从而对雷达部署构成影响。限于篇幅，这些部署问题暂不讨论。

大功率雷达的探测距离虽然很远，但在水平探测时，地球曲率的影响使得雷达的探测距离大为缩小。因此，地球曲率影响下的雷达最大探测距离是一个必须讨论的问题，这也是雷达部署研究的基础。显然，预警雷达离拦截系统越远，发现目标越早，为拦截系统提供的预警时间就越多。但国土疆界是有限的，这限制了预警雷达的部署，从而限制了HCM的预警距离。而拦截作战又需要一定的作战准备时间，那么，预警雷达离拦截系统的距离为多少时能满足作战准备时间需求成为预警雷达离拦截系统的最小配置距离问题。

前面提到，对HCM应尽可能地进行接力跟踪。由于地球曲率的影响，雷达探测距离有限，为了保持相邻雷达探测空间的衔接，相邻跟踪雷达的前后配置间距也是一个必须讨论的问题。

基于上述考虑，本文探讨的问题主要有:1)地球曲率影响下的雷达最大探测距离计算方法;2)预警雷达离拦截系统最小配置距离的计算方法;3)接力跟踪时相邻跟踪雷达前后配置间距计算方法。

为便于研究，提出下面假设:1)不考虑雷达本身的探测能力，只考虑地球曲率对雷达最大探测距离的影响;雷达自身探测能力对抗击HCM部署的限制，将另文讨论;2)来袭HCM目标特性确定、航路确定，只考虑HCM的巡航飞行段，设其在地球上空等高等速飞行;3)抗击HCM的拦截系统部署合理，对HCM构成拦截条件。

1 地球曲率影响下的雷达最大探测距离计算方法

当目标低空飞行或者目标离雷达距离相当远时，雷达对目标的探测距离受地球曲率的影响。为此，首先对地球曲率影响下雷达的实际探测距离进行分析。

2 预警雷达离拦截系统最小配置距离的计算方法

在抗击HCM作战过程中，相关事项时间有:

1)等级转进时间(Δt0)

拦截系统接到HCM预警信息后，进行作战等级转进需要一定的准备时间，主要包括人员就位时间和武器系统开机及状态转换时间，等级转进时间因白天、黑夜而不等。

2)拦截系统制导雷达对目标指示的响应时间(Δt1)

拦截系统接到上级雷达指示的目标信息后，制导雷达对指定空域进行搜索，经历对目标指示的响应时间后，制导雷达截获目标。

3)拦截系统反应时间(Δt2)

从制导雷达截获目标到第一发拦截导弹发射，须经历稳定跟踪、诸元计算、定下射击决心等环节，其间时间称为系统反应时间。

4)拦截弹飞行时间(Δt3)

拦截弹飞行至杀伤区各点时间基本是确定的，拦截弹必须在杀伤区与目标遭遇，否则不能成功拦截目标。

5)航迹形成、信息处理与通信时间(Δt4)

预警雷达发现目标后，需要形成航迹、处理计算目标信息，然后经网络传输到拦截系统，航迹形成、信息处理与通信都需要一定时间。

作战事项与时间的构成可用图2表示。

图2 作战事项与时间构成示意图

设HCM水平飞行速度为vt，飞行高度为ht;拦截系统对HCM杀伤区的最大斜距为rmax。依据尽早拦截的作战原则，设遭遇点位于杀伤区远界，即Δt3取拦截弹飞行至杀伤区远界的时间。设预警雷达发现目标时HCM所处位置为预警点，这样预警点到拦截系统杀伤区远界的最小距离为(Δt0+Δt1+Δt2+Δt3+Δt4)vt，预警点到拦截系统的最小距离为:

这样，在时间上拦截系统才能对目标构成射击条件。

3 接力跟踪时相邻跟踪雷达前后配置间距计算方法

由于HCM突击的目标未知，所以对HCM不仅要尽早预警，还应尽可能地进行接力跟踪。由于地球曲率的影响，雷达探测距离有限，并且相邻雷达之间最好保持一定的衔接空间，因此，接力跟踪时相邻跟踪雷达配置间距便是一个必须讨论的问题。

图3 接力跟踪时相邻跟踪雷达配置间距计算示意图

这就是接力跟踪时相邻跟踪雷达配置间距的计算公式。

4 算例

1)由式(1)，雷达的实际探测距离为

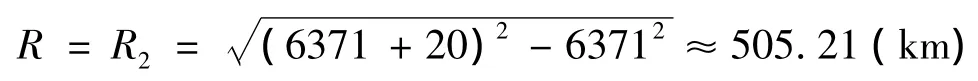
2)等级转进时间一般不大于400s，取较难的情况，设等级转进时间Δt0=400s;制导雷达对目标指示的响应时间Δt1=15s，拦截系统反应时间Δt2=15s，拦截弹飞行至杀伤区高远界时间Δt3=20s;作战体系的航迹形成、信息处理与通信时间Δt4=20s;拦截系统对HCM杀伤区的最大斜距rmax=30 km。

目前，已取得实验成功的HCM飞行速度在5～10Ma之间，为此分几种速度考虑。

1)设HCM水平飞行速度为vt=5Ma=1.7km/s，这样预警点与拦截系统的最小距离为

即以拦截系统配置点为基准，预警雷达至少应在HCM飞至807.76km处发现目标，否则拦截系统在时间上来不及射击。

由式(1)中计算结果，取预警雷达对HCM的最大探测距离为Rmax=500km，这样，预警系统与拦截系统的距离ΔL至少应满足

这表明预警雷达应提前308.16km部署，才能保证目标飞至807.76km处发现目标，为部队提供必须的作战准备时间。

有些制导雷达对目标指示的响应时间、拦截系统反应时间可能大一些，设Δt1=20s，Δt2=20s，则

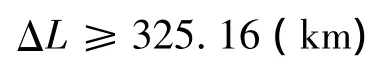
这表明预警雷达应提前325.16km部署，才能提供必须的作战准备时间。

2)若 HCM水平飞行速度达到 vt=10Ma=3.4km/s，制导雷达对目标指示的响应时间、拦截系统反应时间亦取较大的情形，即Δt1=20s，Δt2=20s，其它参数不变，则预警点与拦截系统的最小距离为

即预警雷达至少应在HCM飞至1627.16km处发现目标，否则拦截系统在时间上来不及射击。此时，预警系统与拦截系统的距离ΔL至少应满足

这表明预警雷达至少应配置在拦截系统前1127.56km处。

综合1)和2)，可得下面结论:以拦截系统配置点为基准，在上述假设的参数下，预警雷达配置范围为 (308.16，1127.56)之间。由于拦截系统前1127.56km处很可能已超出国界，因此地基雷达已无法承担预警任务，发展海基、天基预警系统势在必行;同时也说明，HCM在快速突击方面具有很大的优势，对现有防空系统构成巨大压力。

3)取HCM飞行速度为最大的情形vt=10Ma=3.4km/s，跟踪雷达最大高低角εmax=75°，相邻跟踪雷达的交接班时间Δt=20s，则相邻跟踪雷达配置间距

因此，在上述参数下相邻跟踪雷达配置间距不得超过431.03km。

(注:算例中所取数据，主要用于方法验证，与真实系统有一定出入。)

5 结语

合理部署地基雷达，尽早预警、持续跟踪，提供目标信息，是抗击高超音速巡航导弹的基本前提。本文考虑了地球曲率影响，提出了预警雷达离拦截系统最小距离的计算方法，建立了接力跟踪时相邻跟踪雷达配置间距的计算方法，并采用上述方法进行了算例计算，得到了有益的结论。该法对科学部署地基雷达，有效抗击高超音速巡航导弹，具有指导意义。

［1］ Rustam Stolkin，Lucas Vickers，Jeffrey V Nickerson.Using Environmental Models to Optimize Sensor Placement［J］.Sensors Journal，2007，7(3):319-320.

［2］ Michele Garetto，Marco Gribaudo and Carla-Fabiana Chiasserini.Sensor Deployment and Relocation:A Unified Scheme ［J］.Journal of Computer Science and Technology，2008，23(3):400-412.

［3］ K Punithakumar，T Kirubarajan，M Hernandez.Multisensor Deployment Using PCRLBs，Incorporating Sensor Deployment and Motion Uncertainties［J］ .Transactions on Aerospace and Electronic Systems，2006，42(4):1474-1485.

［4］ 王万磊，李侠，周启明，等.雷达网反隐身优化部署决策模型及算法研究［J］.现代雷达，2006，28(11):8-11.(Wang Wanlei，Li Xia，Zhou Qiming，et al.Model and Algorithm of Optimal Anti-stealth Deployment of Radar Network ［J］.Modern Radar，2006，28(11):8-11.)

［5］ 张娟，白玉，窦丽华，等.基于离散化模型的雷达优化配置与部署方法［J］.火力与指挥控制，2007，32(1):22-25.(Zhang Juan，Bai Yu，Dou Lihua，et al.A Optimized Disposition and Deployment Method of Radar Based on Discrete Model［J］.Fire Control＆Command Control，2007，32(1):22-25.)

［6］ 吕月，张冰.雷达组网系统责任区抗干扰优化部署［J］. 火力与指挥控制，2011，36(8):83-86.(Lv Yue，Zhang Bing.Anti-jamming Optimal Arrangement of Radar Networking System with Warning Area［J］.Fire Control＆ Command Control，2011，36(8):83-86.)

［7］ 刘健，罗亮，谢鑫.基于方位限制的反导目标指示雷达配置要求探讨［J］.火力与指挥控制，2013，38(4):57-59.(Liu Jian，Luo Liang，Xie Xin.Study on Requests for Anti-missile Indicating Radar Disposition Based on Azimuth Restriction［J］.Fire Control＆Command Control，2013，38(4):57-59.)

［8］ 白华珍，张德平，王颖龙.地空导弹武器系统抗击TBM时的有效部署区［J］.现代防御技术，2003，31(6):24-27.(Bai Huazhen，Zhang Deping，Wang Yinglong.Effective Deployment Area of the Surface to Air Missile Weapon System Intercepting Tactical Ballistic Missile ［J］.Modern Defense Technology，2003，31(6):24-27.)

［9］ 刘健，王颖龙，聂成.反战术弹道导弹(TBM)战斗部署有关问题探讨［J］.系统工程与电子技术，2001，23(3):66-68.(Liu Jian，Wang Yinglong，Nie Cheng.Some Problems About Anti-TBM Disposition［J］.Systems Engineering and Electronics，2001，23(3):66-68.)

［10］ 刘健，罗亮.高层反导部署方法研究［J］.火力与指挥控制，2012，37(9):85-88.(Liu Jian，Luo Liang.Study on Disposition Method for High-altitude Anti-missile System ［J］.Fire Control ＆ Command Control，2012，37(9):85-88.)

［11］ 丁鹭飞，耿富录，陈建春.雷达原理［M］.北京:电子工业出版社，2009，3.(Ding Lufei，Geng Fulu，Chen Jianchun.Principles of Radar［M］.Beijing:E-lectronic Industry Press，2009，3.)

［12］ 张晓岚，张云，王海涛，等.临近空间高超声速目标及其防御［J］.上海航天，2013，30(1):48-52.(Zhang Xiaolan，Zhang Yun，Wang Haitao，et al.Strategy Analysis Anti-near Space HyPersonic Objective［J］.Aerpspace shanghai，2013，30(1):48-52.)

［13］ 张丽静，刘东升，于存贵，等.高超声速飞行器［J］.航空兵器，2010，43(2):13-16.(Zhang Lijing，Liu Dongsheng，Yu Cungui，et al.Hypersonic Aircrat［J］.Aero Weaponry，2010，43(2):13-16.)