多约束下铰链力矩最优俯冲制导方法*

程 胜 刘鲁华 陈克俊

国防科学技术大学航天科学与工程学院，长沙410073

高超声速飞行器一般以高于5倍声速飞行，大部分飞行空域处于临近空间，相比传统弹道式飞行器，具有响应快速、突防能力强、高效摧毁和高机动性等突出优点，受到各军事强国高度重视［1］。其典型代表有CAV，HTV-2和AHW飞行器［2］，该类飞行器俯冲过程中基本处于高速飞行，并且通常要求快速俯冲，即俯冲段飞行航程很短，再加上大升阻比的构型导致俯冲时调整姿态所需的旋转力矩很大，从而给俯冲过程中姿态控制系统的舵偏转带来极大压力，容易引起铰链力矩过大［3］。铰链力矩是作用在舵面上的气动力对舵铰链产生的力矩［4］，其过大将使舵系统面临结构破坏的潜在危险。主要危害为:铰链力矩增大使舵系统达到饱和，造成姿态控制系统性能迅速下降;另外，一旦引起舵铰链结构破坏，将导致整个飞行器失去控制。故铰链力矩大小对于姿态控制系统实现效果影响极大。

对于舵而言，只要保证铰链力矩的最大值不超限即可保证其正常工作。传统降低铰链力矩一般通过飞行器气动设计实现，而对于不可变形飞行器，实际飞行过程中的气动构型不可再调，铰链力矩无法减小，因此需要另辟蹊径。目前，有关这方面的研究较少，只有文献［3］有过研究。该文献从弹道优化的角度出发，运用Gauss伪谱法和序列二次规划方法，设计铰链力矩最小俯冲弹道。该方法在制导时，需要事先生成铰链力矩最小俯冲弹道，灵活性受到一定限制。

本文从推导解析制导律角度出发，考虑如何降低飞行过程中的铰链力矩。

1 铰链力矩建模

铰链力矩产生的机理为:作用在舵控制面上的控制力(通常为气动力)对舵铰链轴产生的力矩。其大小可通过理论计算、工程估算或实验测试获得。影响铰链力矩的因素很多，为便于研究，主要考虑飞行攻角引起的上洗和舵偏角引起的面-面干扰［5］，文献［6］将铰链力矩展开为:

在制导中，可以利用瞬时平衡假设建立力矩等式。瞬时平衡假设是指不考虑姿态调整的动态过程，认为飞行器始终处于力矩平衡状态，对无动力再入飞行器可表示为:

因此，可将铰链力矩最小俯冲制导在纵平面内转化为法向过载最小俯冲制导。

同理，将式(3)在偏航平面内展开，可将铰链力矩最小俯冲制导在侧平面内转化为侧向过载最小俯冲制导。下面利用最优控制理论求解过载最优的解析制导律。

2 最优制导律推导

2.1 最优制导问题建模

2.2 问题求解

由于状态方程为变系数线性微分方程，若直接求解此最优制导问题，将面临难以求解的Riccati微分方程。一种较简便的解决思路是通过引入伪控制量，将变系数常微分方程转化为常系数微分方程［10］。引入伪控制变量u1:

可见，铰链力矩最小制导律相对于纯比例导引增加了加速度补偿项，并且导航比是时变的。

2.3 控制量解算

制导需要法向过载和侧向过载为:

3 仿真分析

运用文献［12］中的三自由度模型，采用CAV-H飞行器总体和气动参数，设置俯冲起点飞行速度2000m/s，高度 25km，俯冲起点经纬度(1°，1°)，目标点经纬度为(1.3°，1.3°)，初始点速度倾角为0°，速度方位角为-40°，终端速度倾角γDF=-85°，攻角0≤α≤20°，最大过载20g。

仿真结果如图1～5所示。图1～3说明该制导方法能在满足终端落角约束的条件下精确命中目标，其终端位置偏差为0，终端落角偏差为0.02°。图4～5表明攻角、倾侧角指令变化平滑，无振荡，反应到过载上即为过载变化平缓，不会突然出现大过载，这从图9和10的过载曲线(A1曲线)可以得到验证，从而铰链力矩变化稳定。

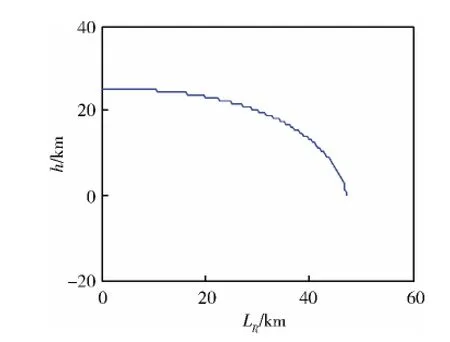
图1 高度-射程曲线

为了重点验证该制导律降低过载的效果，在上面的仿真条件下，将其与式(29)的传统最优制导律［12］进行仿真比较。

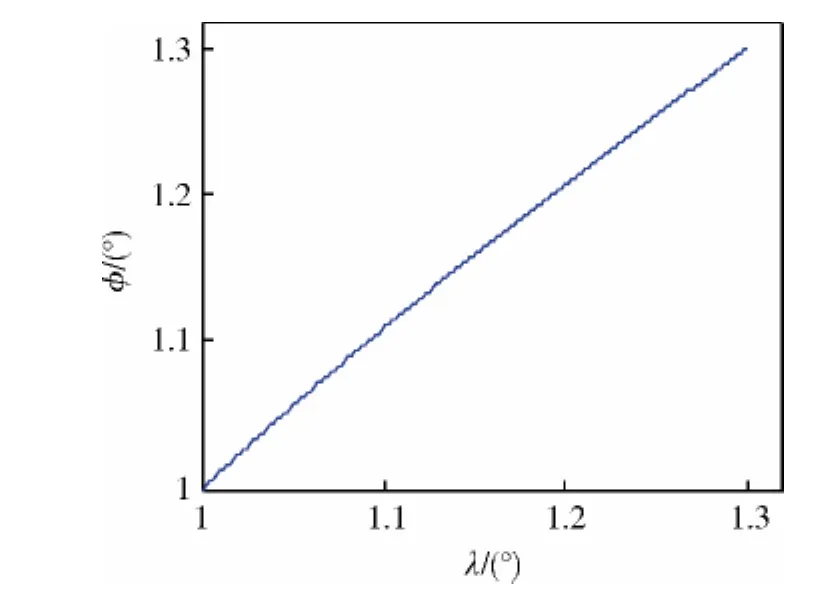
图2 纬度-经度曲线

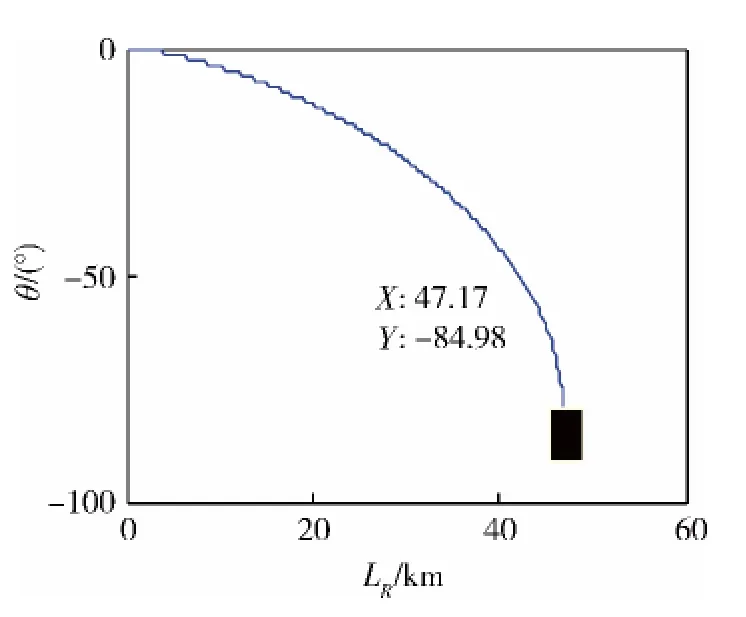
图3 速度倾角-射程曲线

图4 攻角-射程曲线

仿真结果如图6～10所示，图中的A1代表铰链力矩最优制导，A2代表式(29)的最优制导。由仿真结果可以看出，铰链力矩最优制导与式(29)最优制导获得的导引弹道基本相同，都在满足终端落角约束的条件下精确命中目标，但法向过载峰值和侧向过载峰值有明显不同。铰链力矩最优制导的法向过载峰值由式(29)最优制导的13.29g降为11.03g，侧向过载峰值由2.62g降为2.48g。由于式(10)中的系数绝对值远远大于1，可以认为过载小幅减小便会引起铰链力矩大幅度降低，可见本方法的铰链力矩最大值会大大的降低。

图5 倾侧角-射程曲线

图6 高度-射程曲线

图7 纬度-经度曲线

为了进一步验证本方法具有降低铰链力矩的能力，将不同的初始偏差、过程偏差和终端约束偏差下的过载与传统最优制导进行比较。初始偏差取高度偏差Δh=±1 km，速度偏差Δv=±100 m/s，速度倾角和速度方位角偏差Δθ=Δσ =±2°;过程偏差取阻力系数偏差、升力系数偏差和大气密度偏差为ΔCD=ΔCL=Δ ρ=15%;终端约束偏差取落点偏差 Δφ=Δλ=±0.1°，落角偏差ΔγDF= ±5°。

图8 速度倾角-射程曲线

图9 法向过载-射程曲线

图10 侧向过载-射程曲线

结果见表1，表中A1和A2的含义同上文。表中数据表明，无论在何种偏差下，本方法的法向过载和侧向过载都小于传统的最优制导律，从而证明铰链力矩能得到有效降低，体现了铰链力矩最小最优制导的优势。

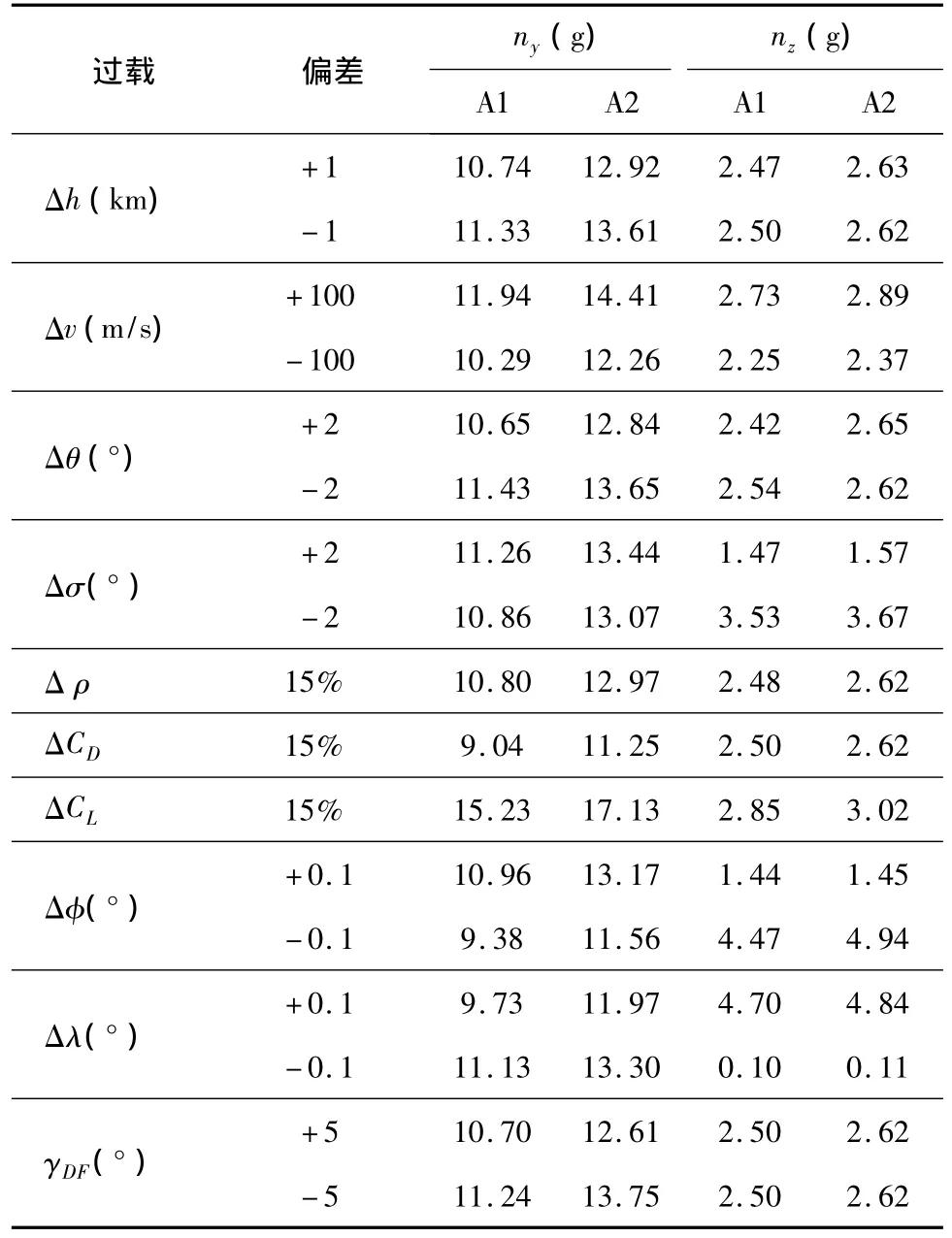
表1 不同偏差下的过载大小情况

4 结束语

针对高超声速飞行器俯冲段铰链力矩过大问题，从制导的角度研究了使铰链力矩降到最小的方法。根据铰链力矩的产生机理，将问题转化为求过载最小。在终端落点和终端落角约束的要求下建立最优问题模型，根据最优控制原理推导出解析形式的最优制导律。仿真验证该制导律能明显降低铰链力矩，且形式简单，可以为高超声速飞行器俯冲段制导控制系统的设计提供参考。另外，本文在制导时并未考虑对终端速度大小的控制，下一步将研究复杂约束下的铰链力矩最小制导方法。

［1］ Xu Mingliang，Chen Kejun，Liu Luhua，et al.Quasi-equilibrium glide adaptive guidance for hypersonic vehicles ［J］.Science China:Technological Sciences，2012，55(3):856-866.

［2］ 韩洪涛，王友利.2013年国外高超声速技术发展回顾［J］. 中国航天，2014(3):16-20.(Han Hongtao，Wang Youli.Hypersonic Technology Development Retrospect of External in 2013［J］.Aerospace China，2014，(3):16-20.)

［3］ 徐明亮，刘鲁华，汤国建，陈克俊.高超声速临近空间飞行器铰链力矩最小俯冲弹道设计［J］.弹道学报，2011，23(3):1-6.(Xu Mingliang，Liu Luhua，Tang Guojian，et al.Design of dive ttajectory of hypersonic near-space vehicle with minimun hinge moment［J］.Journal of Ballistics，2011，23(3):1-6.)

［4］ 吴宗成，朱自强，丁宁，等.三维副翼铰链力矩计算［J］.航空学报，2007，28(3):519-526.(Wu Zongcheng，Zhu Ziqiang，Ding Ning，et al.Calculation of hinge moments of 3-D aileron ［J］.Acta Aeronautica et Astronautica Sinica，2007，28(3):519-526.)

［5］ 汪令羽.全动控制舵铰链力矩计算方法研究［J］.北京理工大学学报，1996，16(4):444-449.(Wang Lingyu.A method for the hinge moments of all-movable controls［J］.Journal of Beijing Institute of Technology，1996，16(4):444-449.)

［6］ Yoonsu Nam，Jinyoung Lee，Sung Kyung Hong.Force Control System Design for Aerodynamic Load Simulator［C］.Proceedings of the American Control Conference.Chicago，2000.

［7］ 鲁建，李邦清，刘永远.一种用舵反馈信号计算铰链力矩的方法［J］.战术导弹与控制技术，2006，52(1):84-85.(Lu Jian，Li Bangqing，Liu Yongyuan.A calculation method of hinge moments used feedback signal of rudder［J］.Tactical Missile and Control Technology，2006，52(1):84-85.)

［8］ 耿建中，曹燚，段辰龙，等.具有速率限制的民机舵面实时铰链力矩特性研究［J］.系统仿真技术，2014，10(1):58-62.(Geng Jianzhong，Cao Yi，Duan Chenlong，et al.research on the real time hinge moment of the control surfaces with rate limiting of civil aircraft［J］.System Simulation Technology，2014，10(1):58-62.)

［9］ 赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997.(Zhan Hanyuan.Vehicle Reentry Dtnamics and Guidance［M］.Changsha:Press of National University of Defense Technology，1997.)

［10］ 连葆华，崔平远，崔祜涛.一种改进的最优制导律及其仿真研究［J］.飞行力学，2001，19(3):36-40.(Lian Baohua，Cui Pingyuan，Cui Hutao.An improved optimal guidance law and Its simulation study ［J］.Flight Dynimics，2001，19(3):36-40.)

［11］ 赵红超，王凤莲，顾文锦.超音速反舰导弹的最优末制导律研究［J］.航空兵器，2005，(3):8-10.(Zhao Hongchao，Wang Fenglian，Gu Wenjin.Research on optimal terminal guidance law for supersonic ant-ship missile［J］.Aero Weaponry，2005，(3):8-10.)

［12］ 陈克俊，赵汉元.一种适用于攻击地面固定目标的最优再入机动制导律［J］.宇航学报，1994，15(l):1-7.(Chen Kejun，Zhao hanyuan，An Optimal Reentry Maneuver Guidance Law Applying to Attack the Ground Fixed Target［J］.Journal of Astronautics，1994，15(l):1-7.)