基于Popov超稳定性的TVC系统在线辨识及补偿方法

陈 童 曾凡铨 崔业兵

上海航天控制技术研究所，上海200233

永磁同步电机以其低惯性、快响应以及高功率密度的特点在航天领域得到了越来越广泛的应用［1］。新一代固体捆绑运载火箭的推力矢量控制(TVC)采用大功率内嵌式永磁同步电机(IPMSM)驱动的电动伺服系统，空间矢量控制采用最大转矩电流比(MTPA)方案。

TVC系统控制的核心在于伺服电机的控制，其电磁环境复杂，且环境温度变化范围为 -40～120℃［2］。在该运行环境下，伺服电机参数摄动问题严重，其中定子相电阻和交、直轴电感的变化影响输出力矩的稳定性和精确度。因此，需要构建控制器自校正系统，以减小电机参数摄动给控制效果带来的不利影响。

由于IPMSM稳态方程欠秩，若不增添补偿方程，在线辨识算法无法精确跟踪时变参数。本文通过分析欠秩问题，提出了一种利用回归分析建模的补偿方案，并基于Popov超稳定性理论，设计了模型参考自适应(MRAS)在线辨识自适应律。该辨识方法利用离线辨识数据，通过两步辨识，摆脱了对数据手册上的参数设计值的依赖，同时减小了在线辨识的运算量。

1 IPMSM数学模型

经过Clarke变换及Park变换，将三相固定坐标系转换为两相旋转坐标系，得到解耦后的IPMSM交、直电流状态方程为:

式中，Rs为定子电阻;Ld，Lq分别为直、交轴电感;id，iq分别为直、交轴电流;ud，uq分别为直、交轴电压;ψf为转子永磁体产生的磁势;ωe为转子电角速度;ωr为转子机械角速度;p为微分算子;Pn为极对数，Te为电磁转矩。

式(1)中，IPMSM伺服系统系数矩阵

2 稳态方程欠秩问题分析

当IPMSM稳态运行，且铁损和涡流损耗忽略不计时，在离散域可以简化为:

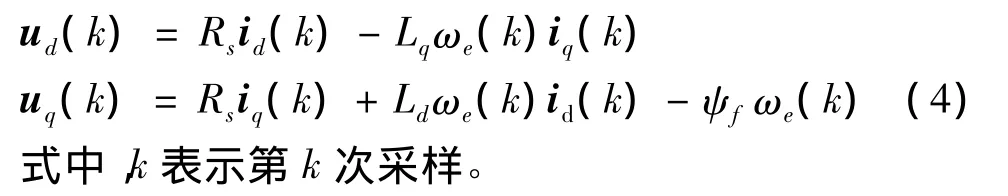
针对火箭伺服系统的特定工作环境，考虑到定子相电阻与永磁体磁链的变化与温度近似呈现线性关系，而交、直轴电感与绕组电流呈现非线性关系。将待辨识参数分组，考虑先将Ld，Lq设置成离线辨识出的初始值，对受温度影响较大的第1组参数(Rs，ψf)首先进行在线辨识，在不同初始参数值及温度变化区间内，统计电阻和磁链的参数值。利用回归分析，拟合出电阻和磁链随温度变化的回归方程，作为第2组参数 (Ld，Lq)在线辨识的补偿方程，以解决IPMSM在线辨识的稳态方程欠秩问题。

3 MRAS在线辨识算法设计

本节基于Popov超稳定性理论，通过参考模型和可调模型输出电流的比较并计算误差，对伺服电机各主要参数的在线辨识自适应律进行设计，并给出了相电阻和转子磁链的回归模型，在线辨识系统如图1所示。

3.1 Popov前向通道补偿

内嵌式永磁同步电机MRAS辨识系统如图2所示。基于Popov超稳定性理论，将可调模型作为前向通道，以自适应律作为反馈通道。

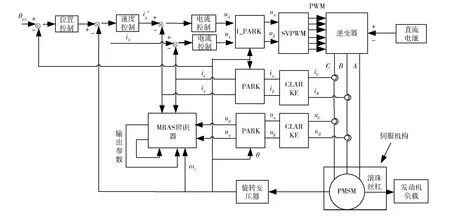
图1 在线参数辨识系统框图

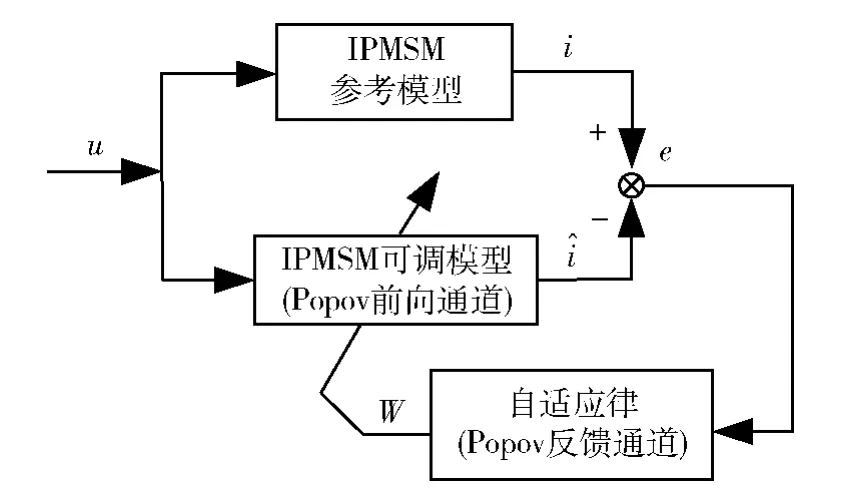
图2 MRAS辨识系统原理图

式(1)即为IPMSM参考模型的状态空间方程，IPMSM可调模型为:

3.2 基于Popov超稳定性自适应律设计

设计相电阻自适应律，应满足Popov的稳定性条件，其误差项微分方程:

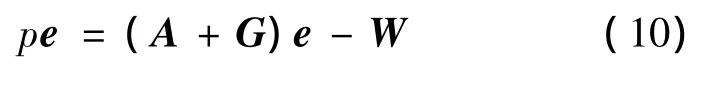
4 电阻、转子磁链辨识数据回归模型

根据记录的在线辨识数据，采用回归分析的方法求解出相电阻和转子磁链的回归方程，本文采用高斯-牛顿法对相电阻、磁链的在线辨识数据进行回归分析。

通过求解电阻温升系数、转子磁链退磁系数，从而求出回归方程，作为交、直轴电感的在线辨识的补偿方程。

相电阻和转子磁链的回归模型分别为:

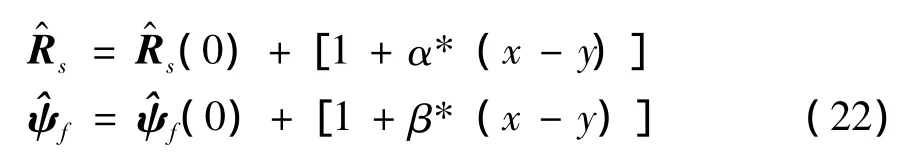
式中，x为在线辨识的温度，y为离线辨识的温度;α，β分别为需求解的电阻温升系数和退磁系数。

5 试验结果分析

试验电机主要参数准确值如表1所示，试验验证基于Popov超稳定性在线辨识及补偿效果。对各个试验温度的辨识结果进行记录，以温度40℃情况为例说明。

表1 试验电机参数准确值(40℃)

相电阻及转子磁链的辨识曲线如图3和4所示。在线辨识的初值设定为各参数的离线辨识值，能够帮助在线辨识快速收敛于实际值，减小振荡过程及程序运算负担。通过观测相电阻及转子磁链辨识曲线，随着交轴电流的增大到一个稳定值，参数估算值经过0.2s收敛于真实值，辨识过程平稳，结果较为准确。

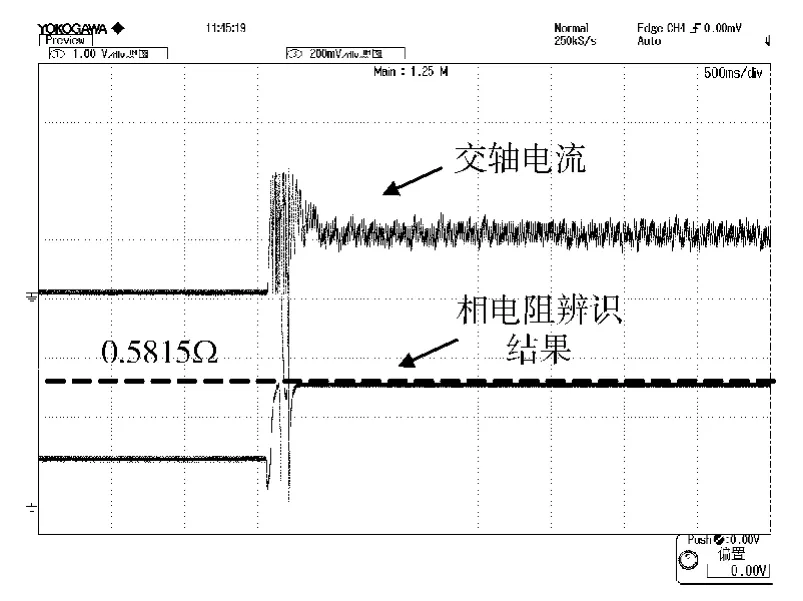
图3 相电阻辨识曲线(40℃)

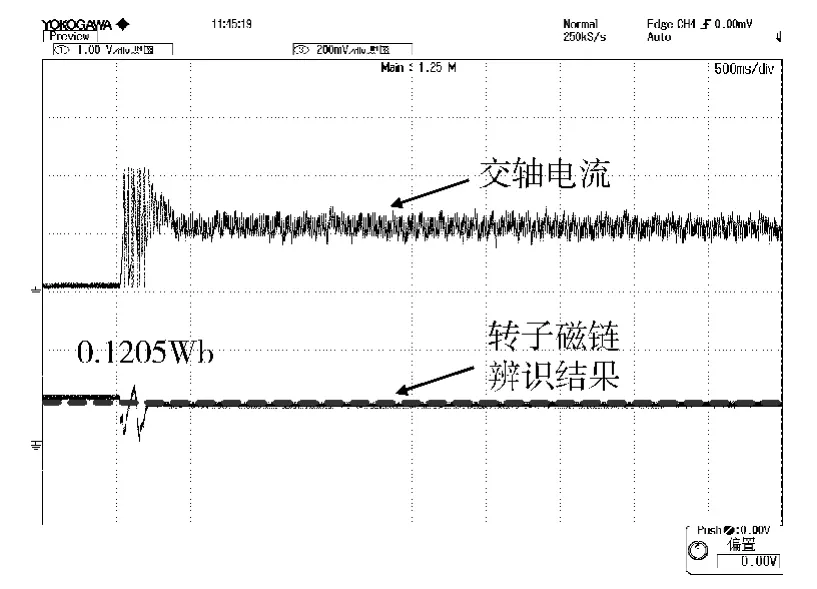
图4 转子磁链辨识曲线(40℃)

对辨识试验结果以10℃为步长统计，在温度区间(10～80)℃内，辨识相电阻Rs和转子磁链ψf的辨识结果如表2和3所示。

表2 相电阻在线辨识结果

表3 转子磁链在线辨识结果

根据表2和3的数据，拟合出试验所用IPMSM相电阻Rs的温度系数α为0.004041，转子磁链ψf的温度系数为-0.0001015.将计算出的温度系数代人式(20)中，作为欠秩问题的补偿方程，用四阶满秩方程进行交、直轴电感Ld，Lq的辨识，在线辨识时相电阻Rs和转子磁链ψf的值由查表的方法获得，得到的交、直轴电感Ld，Lq在40℃的辨识波形如图5和6所示，结果经过约0.15s后收敛。

试验结果表明，IPMSM主要参数估算值与参数准确值相吻合，达到了辨识目的。

6 结论

针对新一代电动TVC系统主要参数，进行了在线辨识及补偿方法进行研究，设计了基于Popov超稳定性理论的自适应参数辨识方案。针对空间矢量控制下的稳态方程欠秩问题，提出利用回归分析进行欠秩补偿，通过两步法辨识伺服电机时变参数。经过试验验证，该方法辨识结果稳定且准确度较高，为系统参数的自校正提供了算法基础，实现了MTPA状态下的满秩在线辨识。

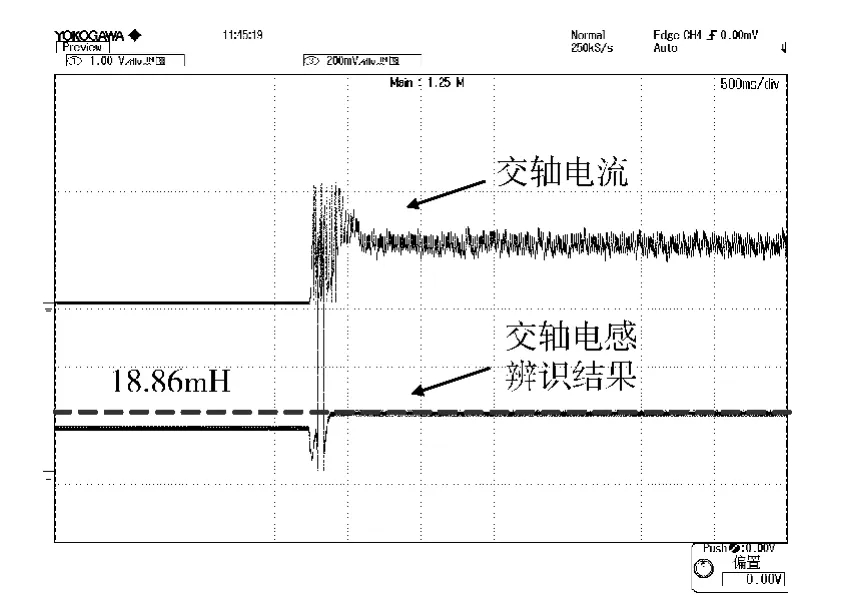
图5 交轴电感辨识曲线(40℃)

［1］ 石立.载人航天高可靠伺服技术［J］.导弹与航天运载技术，2002，(5):49-52.(Shi Li.High reliable servo technology for manned space ［J］.Missiles and Space Vehicles，2002，(5):49-52.)

［2］ 曾广商，沈卫国，石立，等.高可靠三冗余伺服机构系统［J］.航天控制，2005，23(1):35-40.(Zeng Guangshang，Shen Weiguo，Shi Li，et al.High-reliability triple redundancy servomechanism system［J］.Aerospace Control，2005，23(1):35-40.)

［3］ Rash M，Macconnell P F A，Stronach A F，et al.Sensorless indirect-rotor-field-orientation speed control of a permanent magnet synchronous motor with stator-resistance estimation［J］.IEEE Transaction on Industrial Application，2007，54(3):1667-1673.

［4］ 沈艳霞，刘永钦.基于改进型模型参考自适应的PMSM参数辨识［J］.电气传动，2009，39(5):47-50.(Shen Yanxia，Liu Yongqin.Identification of PMSM based on improved model reference self-adaptive algorithm［J］.E-lectric Drive，2009，39(5):47-50.)

［5］ Boileau T，Nahid-Mobarakeh B and Meibody-Tabar F.On-Line Identification of PMSM Parameters:Model-Reference vs.EKF［C］.Proceedings of the IEEE Industry Applications Society Annual Meeting.2008:1-8.

［6］ M.Rahman，Khwaja，Silva Hiti.Identification of machine parameters of a synchronous motor［J］.IEEE Transactions on Industry Applications.2005，41(2):557-565.