基于动力系统求非线性优化的局部最优解
2015-03-10张娜
张 娜
(天津大学 理学院,天津 300072)
基于动力系统求非线性优化的局部最优解
张 娜
(天津大学 理学院,天津 300072)
根据目标函数的拓扑和几何性质求函数的多个局部最优解,建立相关的梯度向量场,求梯度向量场的稳定均衡点,稳定均衡点就是相应目标函数的局部最优解,通过退化点使梯度向量场跳出稳定均衡点的稳定域,在本文中对求退化点的算法进行改进,求非线性优化的多个局部最优解.
梯度向量场;稳定均衡点 ;稳定域;退化点
近年来随着社会的高速发展,全局优化问题在社会上有很广泛的应用,它已经融入我们的日常生活之中,对社会的高速发展有非常重要的作用.全局最优化问题广泛存在于分子生物学、经济金融、数据挖掘与知识发现、环境工程、网络运输、图像处理与模式识别、化学工程设计、工业制造等众多领域,因此受到人们的普遍关注,随着全局最优化问题的广泛应用,在实际生活中,存在着很多的、非常有意义的全局优化模型,然而,全局最优化的困难主要在于,很难跳出当前的局部最优解,得到其全局最优解.而传统的非线性规划方法却很难应用于全局优化问题,因此,全局最优化成为了学者研究的热点之一,随着计算机技术的进步,全局最优化得到了快速的发展,许多全局最优化的理论及算法也相应地得到发展.
H·D·Chiang运用目标函数的拓扑和几何性质求非线性函数的多个局部最优[1],这个方法构造了相关的梯度向量场,用梯度向量场的多个稳定均衡点作为目标函数的局部最优解,给定一个初始点数值积分梯度向量场求出一个稳定均衡点,通过退化点跳出稳定均衡点的稳定域,然后沿着退化点的不稳定流形的反方向运动到另一个稳定均衡点,重复上述过程,找到多个稳定均衡点,这些稳定均衡点就是局部最优解,在本文中对求退化点的算法进行改进,使算法更加简练易懂.
1 定义和概念
本文用一个系统的方法求非线性优化的多个局部最优解,它在本质上是确定性方法.给定一个目标函数,建立这个函数相关的向量场,使得向量场的轨迹收敛到相应的局部最优解.
考虑下面的无约束全局优化问题
min{f(x):x∈Rn}
(1)
其中:f∈C2.假设函数f(x)是有下界的使得函数的全局极小值点存在并且局部极小值点的个数是有限的.
建立与目标函数f(x)相关的梯度向量场[2]

(2)
考虑如下非线性动力系统
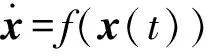
(3)
其中:动力系统的向量x(t)属于欧几里得空间Rn,函数f:Rn→Rn满足解存在性和惟一性的充分条件,称系统(3)在t=0时刻的解曲线x为轨迹,表示为Φ(x,·):R→Rn.
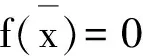
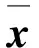
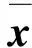
双曲稳定均衡点xs的稳定域表示为:
稳定域A(xs)的边界称为xs的稳定边界,用∂A(xs)表示.实用稳定域(practical stability region)是稳定域一个子集,实用稳定域在求多个局部最优解中有非常重要的应用,稳定均衡点xs的实用稳定域表示为Ap(xs),它是开集intA(xs),退化点是在实用稳定边界上的1类型均衡点.
2 系统的方法
由上节的内容可知函数f(x)的局部最优解和(2)的均衡点是等价的,系统的求多个局部最优解的方法包括如下几步:
1)找到一个局部最优解.
2)从局部最优解出发,沿着函数值增加的方向移动到一个退化点.
3)沿着退化点的不稳定流形的反方向移动并且下降到另一个局部最优解.
第一步可以由下降法求解,第二步非常有挑战性,在下一节中有详细的介绍,第三步涉及到负梯度系统的数值积分.
基于理论的观点,上述的方法可以建立一个图G描述局部最小点和退化点的联系,需要下面的元素:


算法1:求多个局部极小值点
第1步:初始化数据
步骤1:令Vmin=Vd=v=φ
步骤2:找一个初始点x0
步骤3:令ε充分小
第2步:找第一个局部极小值点

第3步:建立相应的图G
WhileV≠φdo
Begin
选择x∈V,令V=V{x}
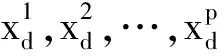
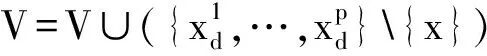
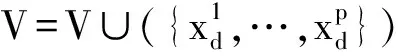
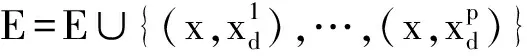
Else
计算J-▽f(x)的不稳定特征向量Eu,数值计算负梯度-▽f(x)初始点分别为x+εEu和x+εEu直到它们达到稳定均衡点y1和y2
令V=V∪({y1,y2}Vmin)
Vmin=Vmin∪{y1,y2}
E=E∪{(x,y1),(x,y2)}
End
我们建立函数相关的反射梯度系统,通过一阶反射梯度系统求退化点,一阶反射梯度向量场F1(x)[4]使f(x)局部极小值点邻域内的点收敛到它稳定边界上的1类 均衡点.可以用下面的方式检验1类均衡点是否是退化点:沿着1类均衡点的Jacobian矩阵的不稳定特征向量的两个方向积分准梯度系统,如果收敛到两个不同的均衡点,则这个1类均衡点是退化点.
算法2:求退化点
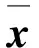
第一步:初始化数据
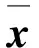
步骤2:选择一个充分大的迭代区间T
步骤3:令ε充分小
第二步:找退化点
Forj=1 topdo

步骤3:检验负梯度向量场-▽f(x)=0均衡点的类型:
如果nj是1类均衡点,计算J-▽f(x)(nj)的不稳定特征向量Eu,数值积分负梯度系统(2),初始点为nj+εEu和nj-εEu直到它们分别到达均衡点y1和y2
如果y1≠y2,D=D∪{nj},
End
3 数值检验
用上述算法求下例的局部极小点
相关的负梯度系统为:
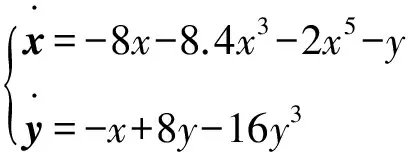

算法结束后,我们发现目标函数有6个局部极小值和7个退化点,结果在表2中,比较局部极小值点的函数值,可以得到函数的全局极小值点为和,全局极小值为-1.0316.
表1 每次迭代的变量值

步骤初始点新的顶点VVminVd1(0.5,0.5)x1s=(-0.0899,0.7126)x1cx1cϕ2x1sx1d=(0,0)x2d=(1.2961,0.6051)x1d,x2d,x3dx1sx1d,x2d,x3d3x1dx2s=(0.0898,-0.7126)x2s,x2d,x3dx1s,x2sx1d,x2d,x3d4x2sx4d=(1.1092,-0.7683)x5d=(-1.12961,-0.6051)x2d,x3d,x4d,c5dx1s,x2sx1d,x2d,x3d,x4d,x5d5x1dx3d=(1.6071,0.5687)x3s,x3d,x4d,x5dx1s,x2s,x3sx1d,x2d,x3d,x4d,x5d6x3sx6d=(1.6381,0.2287)x3s,x4d,x5d,x6dx1s,x2s,x3sx1d,x2d,x3d,x4d,x5d,x6d7x3dx4s=(-1.7036,0.7961)x4s,x5d,x6d,x4dx1s,x2s,x3s,x4sx1d,x2d,x3d,x4d,x5d,x6d8x4dx5s=(-1.6071,-0.5687)x5d,x6d,x4s,x5sx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d
续表

步骤初始点新的顶点VVminVd9x4sϕx5d,x6d,x5sx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d10x5dϕx6d,x5sx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d11x5sx7d=(-1.2961,-0.6051)x6d,x7dx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d,x7d11x6dx6s=(1.7036,-0.7961)x6s,x7dx1s,x2s,x3s,x4s,x5s,x6sx1d,x2d,x3d,x4d,x5d,x6d,x7d13x6sϕx7dx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d,x7d14x7dϕϕx1s,x2s,x3s,x4s,x5sx1d,x2d,x3d,x4d,x5d,x6d,x7d
表2 局部极小值点和退化点

局部最小值点f(·)退化点x1s=(-0.0898,0.7126)-1.0316x1d=(0.0)x2s=(0.0898,-0.7126)-1.0316x2d=(1.2961,0.6051)x3s=(1.6071,0.5687)2.1403x3d=(-1.1092,0.7683)x4s=(-0.7036,0.7961)-0.2155x4d=(1.1092,-0.7683)x5s=(-1.6071,-0.5687)2.1403x5d=(-1.2961,-0.6051)x6s=(1.7036,-0.7961)-0.2155x6d=(1.6381,0.2287)x7d=(-1.2961,-0.6051)
4 结 语
在本文中,用动力系统求非线性函数的多个局部极小值点,在算法1中的第二步,本文中用拟牛顿法求局部极小值点,相比以前积分的方法更简单精确度更高,在算法2中,本文求的零点,这个方法更直观便于理解,通过准梯度系统 和反射梯度系统之间的转换可以求出多个局部极小值点和退化点,通过比较局部极小值点的值可以得到全局极小值点.最后需要进一步改进的是如何得到所有的退化点.
[1] ALBERTO L F C, CHIANG H D, Characerization of stability region for general autonomous nonlinear dynamical systems [J]. IEEE Tran. Automat Contr, 2012, 57(6): 1564-1569.
[2] DEMARCO C I. Approximating power system dynamics and energy functions by quasi-gradient models [J]. Intern. Sympos. on Circuits and Systems, 1989, 2: 1966-1969.
[3] HIRSH M W, SMALE S. Differential equation, dynamical systems and linear algebra [M]. New York:Academic.1974.
[4] JONGEN H T, JONKER P, TWILT F. Nonlinear optimization in RN [M]. Verlag Peter Lang, 1986. 102-103
[5] 严太山,崔杜武.求解无约束优化问题的知识进化算法及其收敛性分析[J]. 控制理论与应用, 2010, 27(10): 1376-1382.
Obtaining local optimal solutions of nonlinear programming problems based on gradient system
ZHANG Na
(School of Science, Tianjin University, Tianjin 300072, China)
According to the topological and geometric properties of the objective function the multiple local optimal solutions were solved, and relevant gradient vector field of the function was established. The stable equilibrium of the gradient vector field was the local optimal solution of the corresponding objective function. Through degradation point of gradient vector field seeks for the stable equilibrium. This paper improved the method of degradation point algorithm and solve nonlinear optimization of multiple locally optimal solutions.
stable equilibrium point; gradient vector field; stability region; degradation point
2014-12-04.
张 娜(1991-),女,硕士,研究方向:动力系统与优化.
O224
A
1672-0946(2015)06-0744-04
