基于改进边际优化算法的备件配置研究*1



基于改进边际优化算法的备件配置研究*1

董琪1a，徐廷学1b，杨继坤2，赵建忠1b

(1．海军航空工程学院,a．研究生管理大队，b．兵器科学与技术系，山东 烟台264001；

2．中国人民解放军92493部队，辽宁 葫芦岛125000)

摘要：针对传统边际优化算法在解决备件配置优化问题存在运算效率不高的问题，提出了基于改进边际优化算法的备件优化配置方法。在传统边际优化算法思想的基础上，提出了改进的边际优化算法，通过引入备件短缺系数，提高了算法的优化效率。给出了该优化算法的设计思想和优化流程，并在理论上分析了算法的优化效率。通过算例数值结果的分析，验证了算法在保持最优解精度的情况下，大幅提高了运算效率，为备件库存配置优化提供了指导。

关键词：备件；优化配置；边际优化算法；系统可用度；备件短缺系数；库存系统

0引言

随着武器装备规模、复杂性的不断增加，装备保障技术，特别是影响大规模、复杂装备系统达到战备完好性要求的备件优化配置研究显得越来越重要。通过构建有效的分析模型以确定装备系统的最优备件配置方案是备件优化配置技术的核心内容。统计表明，在相同的情况下，合理的备件配置模型确定的库存水平与部队惯用的单项法相比，可降低40%～50%[1]。许多学者也通过不同的方式验证了优化配置建模在备件配置应用中的优点[2-3]。

一般来说，对装备系统库存问题的求解普遍采用多品种备件多级最优库存建模，该模型通常根据不同的假设条件，在多级多站点的保障系统结构下，以系统可用度为约束条件、配置费用最少为目标或者以配置费用为约束条件、系统可用度最大为目标建立模型并确定备件的配置方案。这些模型的求解常采用METRIC法(multi-echelon technique for recovery item control)。该方法的核心思想是通过边际优化算法对各级各站点仓库进行备件分配，从而确定出各级各站点仓库的备件初始配置量[4]。

目前，国内外学者针对备件优化配置及其优化算法开展了大量研究，取得了较大的进展。文献[5-7]从备件保障系统结构的角度，建立了从两级到多级的备件配置优化模型。解决多级保障系统备件配置优化问题，选择合理的优化算法是关键。常见的用以解决METRIC模型的优化算法是边际优化算法，尽管文献[8-9]利用分层思想对边际优化算法进行了改进，但该方法将装备系统作为串联结构进行处理，而随着装备结构复杂性的增加，该方法具有一定局限性。也有文献利用相关回归方法[10]及拉

格朗日乘子法[11]对模型进行优化。另外，以遗传算法[12]、粒子群算法[13]、神经网络[14]等为代表的智能算法也越来越多应用于解决备件配置优化问题，这些方法虽然运算效率较高，但其优化分析过程不直观，无法为决策者提供更多直观辅助信息。相比之下，边际优化算法在这方面有着无可比拟的优势。常见的备件优化软件如OPUS10，V-METRIC等[1]均基于边际优化算法开发的，但该算法存在着计算量大，运算效率低的缺点。

综上所述，本文针对边际优化算法的运算效率偏低，通过建立基于METRIC的多级备件配置模型，在分析传统边际优化算法的基本原理的基础上，引入了备件短缺系数，提出了改进的边际优化算法，并给出了基本原理和优化步骤。

1基于METRIC的多级备件配置模型

1.1问题描述及符号说明

多级备件保障系统通常e个保障层级，其中e=0,1,…,E；在第e层级上存在n(n=1,2,…,Ne)个仓库站点；M表示备件保障系统所保障的装备数量；i(i=1,2,…,I)为所保障的备件种类，如图1所示。构建备件配置模型的目的是确定各层级仓库关于各类备件的库存水平，以满足约束条件下的系统库存目标最优。

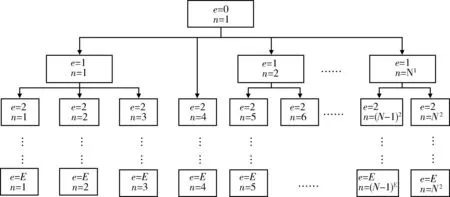
图1　多级备件保障系统网络结构图Fig.1　Supply network of multi-echelon spare parts system

文中所用到的其他符号说明如下：

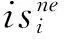
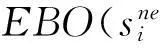
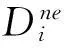
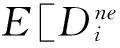
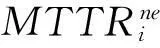
γ：备件短缺系数；

Zi：备件i在一个装备上的机用数；

C：系统备件配置总费用。

1.2基本假设

根据以上描述，结合METRIC模型的基本假设条件，现作假设如下：

(1) 保障系统内周转的备件均为可修复备件，其维修过程即为备件的周转过程；

(2) 各层级仓库对备件的需求服从独立的泊松分布，其维修分布满足Palm定理；

(3) 备件保障系统不存在备件横向转运；

(4) 各级仓库的库存检查策略为(s,s-1)策略；

(5) 整个备件保障系统的供应链守恒，即无备件报废；

(6) 不同种类备件的短缺代价相同；

(7) 各级维修站点采用“先到先修”的原则处理失效备件，且维修能力无限。

1.3模型构建

根据METRIC建模理论，首先计算在周转期t内，备件需求服从泊松分布条件下，保障层级e上保障站点n关于备件i的待收库备件数的稳态概率分布：

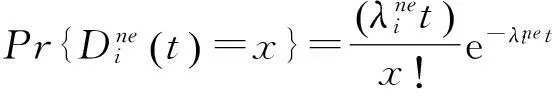
(1)

当t时刻，保障站点的库存量小于备件需求量时，则会出现备件短缺的情况，短缺量为

(2)

由于备件配置的目标是确定各仓库最优的稳态库存水平，因此，需要计算保障层级e上保障站点n关于备件i的期望短缺量，如下：

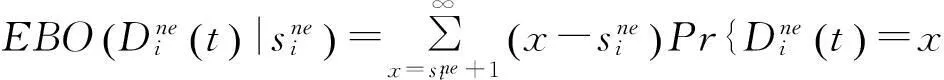
(3)

当多级备件保障系统维修建模过程可参考文献[4,8]构建。

METRIC模型的优化配置目标函数一般是系统可用度函数，也有学者使用备件期望短缺量作为优化目标。通过系统可用度可以更好分析备件方案的费效全过程，更有利于说明不同优化算法的优化效果，因此，本文采用系统可用度为系统效能指标。

由装备可用度定义，在备件期望短缺量计算公式的基础上得到了系统可用度表达式：

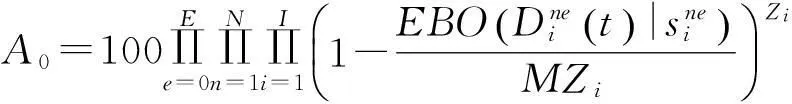
(4)

由此可知，备件保障方案的确定需要综合考虑系统可用度、备件期望短缺数、备件需求、备件延误等因素。

于是，构建系统备件配置模型为

目标函数

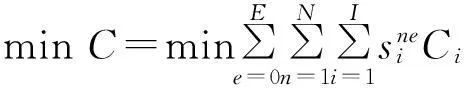
(5)

约束条件

s.t.A0≥A,

(6)

式中：Ci为第i个备件的配置费用；A为规定的系统可用度要求。

由式(5)，(6)组成的系统备件配置模型属于典型的METRIC模型。

2基于边际优化算法的备件配置优化

传统的边际优化算法属于一种渐进的优化方法。其基本思想为[15]：首先，将因变量变化值与自变量变化值的比值称为边际值；其次，根据本文实际，确定边际成本与边际收益，以及模型控制变量，本文所研究备件优化问题的控制变量显然为系统需配置的备件数量；其次，通过对控制变量加1，计算各边际单元每单位控制变量总效益的增量(即边际效益)，根据边际效益分析，确定需增加备件配置量的单元，并对该单元备件配置量加1；最后，当满足条件时，迭代停止。

针对本文模型和实际条件，具体应用步骤如下：

步骤1： 将式(4)进行取对数处理，将系统可用度转化为备件短缺量之和，便于后期计算：

(7)

步骤2： 初始化各站点备件库存量，一般在初始阶段各站点库存量为0。

步骤3： 计算每次迭代的边际效益值：

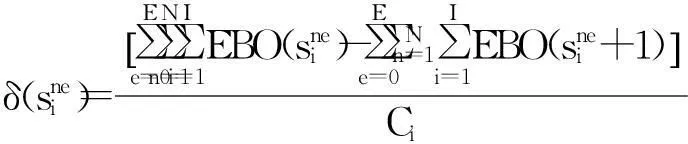
(8)

步骤5： 将步骤4结束时的库存量作为下一次迭代的初始库存量，按照步骤3和步骤4反复迭代，直到满足模型中系统可用度要求为止。

3改进的边际优化算法

传统边际优化算法的原理类似于“贪婪算法”，通过模型通过边际优化算法达到目标最优解时，其计算量由备件种类数、仓库站点数量和约束条件要求共同决定，如果一个库存系统1 000种备件，各级仓库共100个，那么利用边际优化算法进行一次迭代至少需要1×105次计算，当求得最优解时，需要多百万或千万次计算[16]。

针对传统边际优化算法存在计算效率偏低的确定，本文提出了改进的边际优化算法。其基本思想是：首先，通过引入备件短缺系数确定各仓库备件的初始库存量；其次，每一次迭代都来源于前一次的“批量”计算，这种“批量”是与传统边际算法相对应的，由于传统边际优化算法每一次迭代都是在站点现有库存量基础上加1进行决策，而改进算法通过备件短缺系数在站点现有库存量基础上加m，m的取值是由备件短缺系数和现有库存量共同决定的。这样，改进的优化算法就可以简化计算，提高计算效率。

改进的边际优化算法步骤为：

改进的边际优化算法流程如图2所示。

4算例分析

某装备保障系统为三级保障体制，各级保障结构及关系如图3所示。该保障系统两级之间的备件周转期均为120天，采用的修理方式为换件维修，装备备件相关参数如表1所示,其中C为各仓库站点配置一个备件的费用(单位为元)；D为各仓库站点关于备件的年需求量；MTTR为各维修机构关于备件的平均修复时间(单位为天)。

改进的边际优化算法的优点在于保持模型精度的同时可有效降低算法的迭代次数，为验证本文算法的效率，且不失一般性，将控制参数取不同值，得到多种不同条件下模型的优化结果，并与同等条件下传统边际优化算法进行对比。

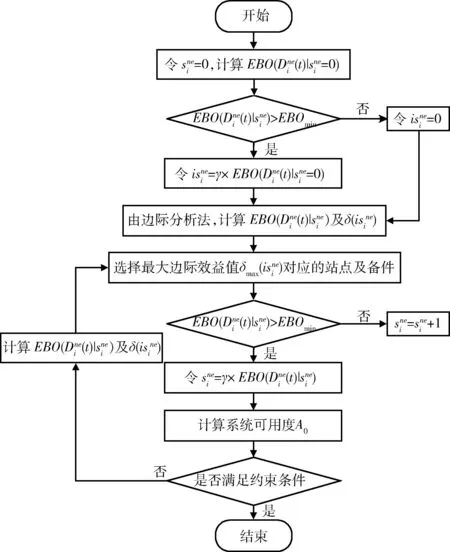
图2　改进边际优化算法流程图Fig.2　Flow chart of the improved marginal algorithm

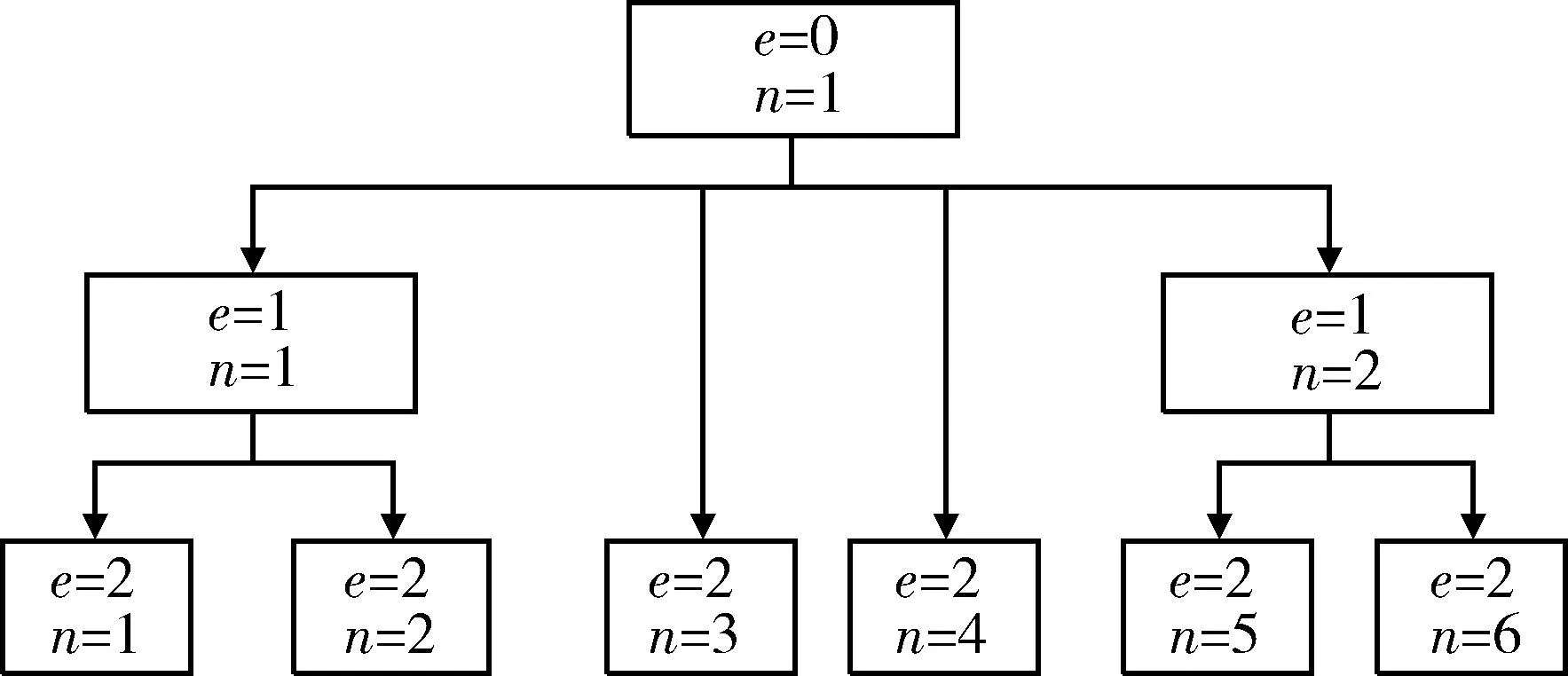
图3　某装备保障系统结构图Fig.3　Supply network of the equipment support system

站点e=0n=1e=1n=1e=1n=2e=2n=1e=2n=2e=2n=3e=2n=4e=2n=5e=2n=6C757575100125100125100125D7003002001251751257512575MTTR903030303030303030

本文采用的备件配置模型为METRIC模型，该模型的控制参数为备件配置费用C、备件需求率λ、系统可用度A0，其中备件需求率λ可由备件年需求量D求得。首先将前2个控制参数取不同值，取值的原则是用(0，-，+)分别表示控制参数取原值不变，原值减小50%，原值增加50%，于是可以得到9种不同的条件。在此基础上，令优化模型的约束条件，即系统可用度要求A分别取0.90，0.95，0.99，同时取γ=0.25，EBOmin=30。利用改进的边际优化算法计算得到系统的配置总费用，以及算法的迭代次数如表2所示，其中系统迭代次数由ITER表示，系统配置总费用由Cs表示。

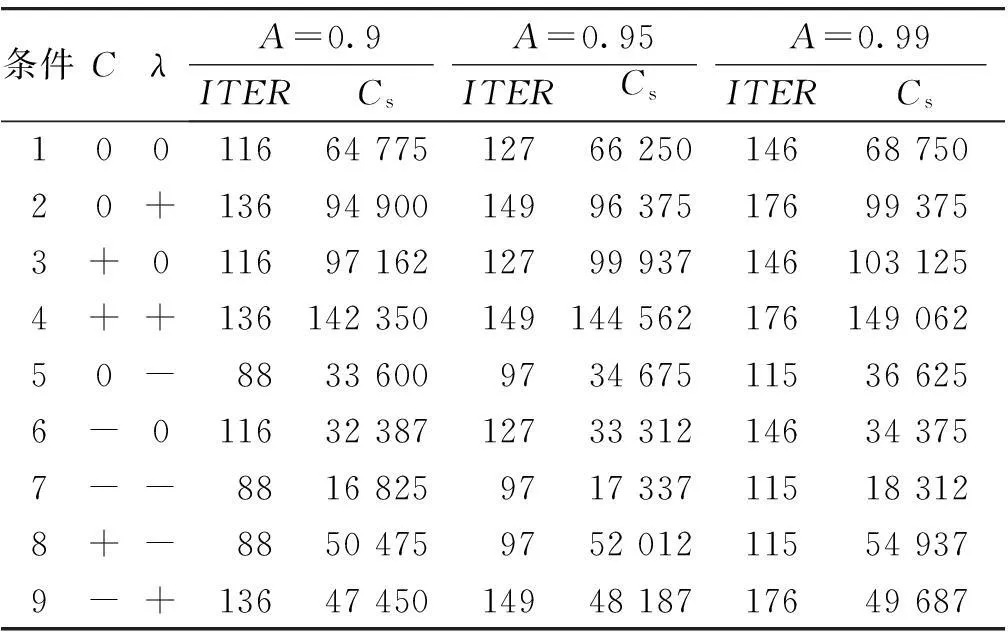
表2　改进边际优化算法计算结果

由传统边际优化算法计算得到结果如表3所示。

表3　传统边际优化算法计算结果

由表1和表2计算结果对比可知，改进的边际优化算法可在保持优化结果精度的前提下，大幅降低算法的迭代次数，提高计算效率。计算结果对比如图4所示，其中曲线ITER1，ITER2，ITER3分别表示可用度要求在0.90，0.95，0.99时，改进算法与传统算法在9种条件下达到最优解的迭代次数之比；曲线C1,C2,C3分别表示可用度要求在0.90,0.95,0.99时，改进算法与传统算法在9种条件下达到最优解之比。

图4　计算结果对比Fig.4　Experiment results of various algorithms

从图4可以看出，当γ取0.25，在9种不同参数组合的条件下，改进的边际优化算法求得最优解的迭代次数最多为传统边际优化算法迭代次数的30%，而改进算法与传统算法求得的最优解精度误差保持在0.8%内。因此，改进的边际优化算法明显提高了运算效率，且保证了求得最优解的精度。

改进的边际优化算法通过引入备件短缺系数γ，提高了运算效率，而γ的取值对于算法至关重要。因此，需分析不同γ值对算法优化效果的影响。取γ分别为0.25,0.5,0.75，且保持算例其他参数不变，得到9种条件下优化结果与传统算法优化结果的比率，如图5所示。图中计算结果(包括迭代次数和最优解)的均值比率由I-Ave和C-Ave表示、计算结果中最小值的比率分别由I-Min和C-Min表示，以及最大值的比率分别用I-Max和C-Max表示。

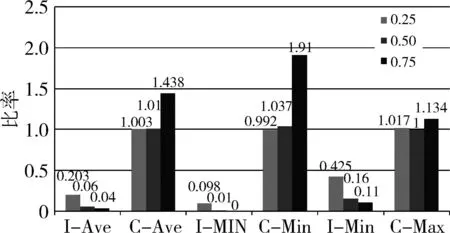
图5　不同γ值下计算结果对比Fig.5　Experiment results with various γ

由图5分析可知，随着γ从0.25增至0.75，所求得最优解的迭代次数由传统边际算法迭代次数的20.3%逐渐降至4%，计算效率逐渐增加，而且当γ取0～0.5时，计算效率提升效果比γ取0.5～1时更加明显。在最优解求解精度方面，随着γ从0.25增至0.75，精度逐渐下降；当γ=0.25和0.50时，改进边际优化算法得到的最优解均值与传统边际算法的偏差均控制在1%以内；但当γ增至0.75时，偏差增大到43.8%，明显高于γ=0.25和0.50时的计算结果。综上所述，γ的取值应根据计算时间和计算精度的要求进行权衡。在对精度要求不高，而时间要求较高的工程领域，γ可取0.50～0.75之间的数值；若对计算精度要求较高，则γ应取0～0.50之间的数值。从以上分析来看，对计算时间和精度均有较高要求时，γ取0.50附近的数值最为合理，以本文结果为例，计算时间和精度偏差的均值分别控制在6%和1%，优化效果明显。

5结束语

本文采用系统优化效能优化思想，在基于METRIC模型的基础上构建了以系统可用度为约束条件，以系统备件配置总费用为优化目标的装备备件多级配置模型，并提出了改进的边际优化算法。算例表明了改进边际优化算法在适用于多级备件保障系统的同时，明显提升了运算效率，其有效性和实用性得到增强。未来可进一步分析该算法在其他条件下备件配置模型应用的可行性，例如考虑同级仓库间横向调拨、备件串修的情况等。

参考文献：

[1]任敏，陈全庆，沈震．备件供应学[M]．长沙：国防工业出版社，2013：140-145.

REN Min, CHEN Quan-qing, SHEN Zhen. The Theory of Spare Parts Supplies [M]. Changsha: National Defense Industry Press, 2013: 140-145.

[2]王乃超，康锐．基于备件保障概率的多级库存优化模型[J]．航空学报，2009，30(6)：1043-1047.

WANG Nai-chao, KANG Rui. Optimization of Multi-Echelon Repariable Item Inventory Systems with Fill Rate as Objective [J]. Acra Aeronautica ET Astronautica Sinica, 2009, 30(6): 1043-1047.

[3]郭强,张振友,黄立坡,等．基于METRIC理论的防空武器系统备件配置优化[J]．火力与指挥控制，2011，36(8)：100-106.

GUO Qiang, ZHANG Zhen-you, HUANG Li-po, et al. Research on Optimization of Disposition of Spare Parts for Air Denfence Weapon System Based on Metric Theory[J]. Fire Control & Command Control, 2011, 36(8): 100-106.

[4]SHERBROOKE CRAIG C. Optimal Inventory Modeling of Systems: Multi-Echelon Techniques[M]. New York: Springer Science Business Media, 2004.

[5]周伟，刘亚杰，郭波，等．基于两级供应关系的武器装备贵重件初始配置模型[J]．系统工程理论与实践，2011，31(6)：1056-1061.

ZHOU Wei, LIU Ya-jie, GUO Bo, et al. Initial Configuration Model About the Valuable Parts of Weapon System Based on Two-Class Supply Relationship [J]. System Engineering- Theory & Practice, 2011, 31(6):1056-1061.

[6]付兴方，李继军，李宗植．基于两级供应关系的可修复航材存储策略模型研究[J]．系统工程理论与实践，2004，24(2)：111-115.

FU Xing-fang, LI Ji-jun, LI Zong-zhi. A Stock Strategy Model for Restorable Air Material Based on Two-level Providing Condition [J]. System Engineering- Theory & Practice, 2004, 24(2): 111-115.

[7]张琳，赵杰，唐超，等．可维修备件库存模型研究[J]．兵工学报，2009，30(11)：90-94.

ZHANG Lin, ZHAO Jie, TANG Chao, et al. Research on the Echelon Inventory Model of the Repairable Spares [J]. Acta ArmamentarII, 2009, 30(11): 90-94.

[8]阮旻智，李庆民，李承，等．改进的分层边际算法优化备件的初始配置方案[J]．兵工学报，2012，33(10)：1251-1257.

RUAN Min-zhi, LI Qing-min, LI Cheng, et al. Improved-Layered-Marginal Algorithm to Optimize Initial Spare Part Configuration Project[J]. Acta ArmamentarII, 2012, 33(10): 1251-1257.

[9]赵建忠，李海军，叶文，等．改进系统备件满足率约束下的备件优化配置建模[J]．兵工学报，2013，34(9)：1187-1192.

ZHAO Jian-zhong, LI Hai-jun, YE Wen, et al. Optimization Configuration Modeling of Spare Parts Under Constraint of Improved System Spare Part Fill Rate[J]. Acta ArmamentarII, 2013, 34(9): 1187-1192.

[10]LEE H L. A Multi-Echelon Inventory Model for Repairable Items with Emergency Lateral Transshipments [J]. Management Science, 1987, 33(10): 1302-1316.

[11]AL-RIFAI M H, ROSSETTI M D. An Efficient Heuristic Optimization Algorithm for a Two-Echelon (R, Q) Inventory System[J]. International Journal of Production Economics, 2007，109(2): 195-213.

[12]SARANGA H, KUMAR U D. Optimization of Aircraft Maintenance Support Infrastructure Using Genetic Algorithms-level of Repair Analysis[J]. Ann Oper Res, 2006, 143(1): 91-106.

[13]刘少伟，金荣，张琳．用粒子群算法优化装备初始备件量[J]．空军大学学报:自然科学版，2008，9(1)：46-49.

LIU Shao-wei,JIN Rong, ZHANG Lin. The Optimization of Initial Spare Parts Based on Particle Swarm Optimization Algorithm[J]. Journal of Air Force Engineering University:Natural Science ed, 2008, 9(1): 46-49.

[14]刘刚，钟小军，董鹏．基于遗传算法和神经网络的舰船电子装备备件优化模型研究[J]．舰船科学技术，2008，30(5)：138-142.

LIU Gang, ZHONG Xiao-jun, DONG Peng. Research on Warship Electronic Equipment Spare Parts Optimize Model Based on Genetic Algorithm and Neural Network[J].Ship Science and Technology, 2008, 30(5): 138-142.

[15]蔡泽明，康锐，龙军．面向系统优化的备件动态配置方法[J]．系统工程与电子技术，2010，32(11)：2363-2366.

CAI Ze-ming, KANG Rui, LONG Jun. System Optimization-Oriented Dynamic Spares Configuration Method[J]. System Engineering and Electronics, 2010, 32(11): 2363-2366.

[16]RAPPOLD J A, TCHERNEV N. Designing Multi-Echelon Service Parts Networks with Finite Repair Capacity[J].European Journal of Operational Research, 2009, 199(3): 781-792.

Improved Marginal Algorithm for Spare Parts Configuration

DONG Qi1a, XU Ting-xue1b, YANG Ji-kun2, ZHAO Jian-zhong1b

(1．Naval Aeronautical and Astronautical University, a. Graduate Students’ Brigade,b.Department of Ordnance Science and Technology,Shandong Yantai 264001，China；2.PLA，No. 92493 Troop, Liaoning Huludao 125000, China)

Abstract:An improved marginal algorithm for spare parts configuration is proposed to overcome the traditional marginal algorithm of poor efficiency in spare parts configuration. The improved marginal algorithm that introduced fraction of the EBO (expected backorder) of qualified spare parts is proposed, and the computational efficiency is improved. The detailed design and optimization of the proposed algorithm is given, and the optimization efficiency is analyzed in theory. The calculated result of an example shows that the efficiency of improved marginal optimization algorithm is much higher than that of traditional algorithm with high accuracy. The research result can provide guidance for spare parts optimization configuration in engineering application.

Key words:spare part; spare optimization; marginal optimization algorithm; system availability; expected backorder(EBO) index; inventory system

中图分类号：E92；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-05-0198-07

doi:10.3969/j.issn.1009-086x.2015.05.032

通信地址：264001山东省烟台市芝罘区二马路188号206教研室E-mail：lance0627@163.com

作者简介：董琪(1986-)，男，河南平顶山人。博士生,研究方向为装备综合保障建模与仿真。

*收稿日期：2014-09-17；修回日期：2015-02-06