时频图像二维EMD分解在LPI信号识别中的应用*1



时频图像二维EMD分解在LPI信号识别中的应用*1

张帆1，刁鸣1，杨承志1,2

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨150001;

2. 空军航空大学 信息对抗系，吉林 长春130022)

摘要：针对LPI信号分类识别问题中，时频图像受噪声干扰严重的问题，提出了一种基于二维快速经验模式分解(FBEMD)的图像降噪算法，并利用该算法实现对LPI信号的分类。首先利用时频分析方法，获得待分类信号的时频分布图像；使用二维EMD分解算法对图像降噪；截取包含时频信息的图像部分，通过主分量分析法提取特征矢量；最后采用RBF神经网络完成信号的分类识别任务。对常见的LPI雷达信号进行仿真，结果表明较低信噪比情况下，该方法仍能获得较好的分类结果。当信噪比为-2 dB时，采用二维EMD降噪算法，平均正确识别率能够达到93%。

关键词：LPI雷达信号；时频分布；二维EMD分解；主分量分析

0引言

近年来，雷达技术不断发展，信号频率范围更大，信号调制特征更复杂，传统雷达信号的五大参数难以有效描述雷达信号，信号识别要求难以满足。同时在复杂的战场电磁环境下，截获的信号必然存在大量噪声干扰，较低的信噪比使得雷达信号的识别更加困难。

近年来，利用时频分析技术与数字图像处理技术相结合，实现对LPI信号的识别和分类的方法，引起了大量学者的关注。文献[1-2]使用了一种将时频图像二值化，利用图像处理形态学中的腐蚀和膨胀降噪，完成分类的算法；文献[3]提出一种利用二维高斯低通滤波器处理时频图像，完成分类的算法；文献[4]利用自适应维纳滤波对图像处理，二值化后提取局部二值模式纹理特征完成分类。还有大量研究，重点关注对时频图像特征的提取，如利用伪Zernik矩阵[2]、时频图像代数特征[5]、二维主分量分析[6]等。这些算法中，对LPI(low probability of intercept)雷达信号时频图像的降噪处理研究不深，降噪同时无法有效保留图像的高频细节信息，对分类正确率有很大的影响。

2003年J. C Nunes.[7]将基于经验的模式分解算法(empirical mode decomposition，EMD)推广到二维领域，提出了二维EMD算法。近几年来，二维EMD分解被大量学者深入研究，广泛应用于图像去噪[8]、图像融合[9]等领域。

针对上述问题，本文提出一种利用时频图像二维EMD分解和重构算法的LPI信号分类方法。

1基于时频图像处理的LPI信号分类方法

本文首先通过二维EMD分解和重构对获取的LPI雷达信号的时频图像进行预处理；然后利用奇异值分解与主分量分析相结合的方法提取时频图像特征矢量， 根据特征矢量完成对LPI雷达信号的调

制识别。具体流程如图1所示。

1.1时频分析

时频分析能把时域信号映射到二维的时频平面上，能够同时从时域和频域描述信号，对信号描述更加精确。Wigner-Ville分布(WVD)是一种具有边缘特性、时移频移不变性、实值性等特性的时频分析方法，而且对线性调频信号有着良好的能量集中性。因此，文中选择了加窗的伪Wigner-Ville分布(PWVD)进行分析,其定义为

(1)

式中：s(t)为受噪声干扰的信号；h(t)为窗函数。本文采用了7种LPI雷达信号，包括BPSK信号、COSTAS信号、FRANK信号、FMCW信号、P1信号、P2信号、PT1信号， 其PWVD时频图像如图2所示。从时频图像中，可以发现有明显的交叉项，但本文采用该种时频分析方法，主要用于完成对不同降噪算法的对比，故本文中不对交叉项的抑制进行详细研究。

1.2基于二维快速EMD算法的时频图像预处理算法

根据对LPI雷达信号的PWVD结果的分析，可以发现时频图像中，不仅包含与信号有关的时域和频域特征，也包含大量的高频噪声、无信号区域等冗余信息。噪声干扰使分类能力降低；冗余信息使得时频图像数据尺寸过大，直接进行分类大大增加计算量。因此，降低噪声干扰、去除冗余信息是对LPI雷达信号正确、迅速分类必须完成的任务。

1.2.1二维快速EMD算法

完成EMD分解算法，需要首先找到最佳的局部均值。传统EMD分解确定信号的极大极小值点，通过插值算法构成上下包络线，最后利用上下包络线求均值。快速二维经验模式分解算法，基于矩阵变换，减少了求极值的计算，提高了EMD算法效率。FBEMD(two-dimensional fast EMD)的核心思想是利用均值滤波矩阵组求矩阵邻域均值[10]：

图1　基于图像处理的LPI信号分类流程Fig.1　LPI signal classification process based on image processing

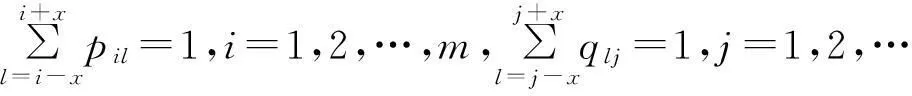
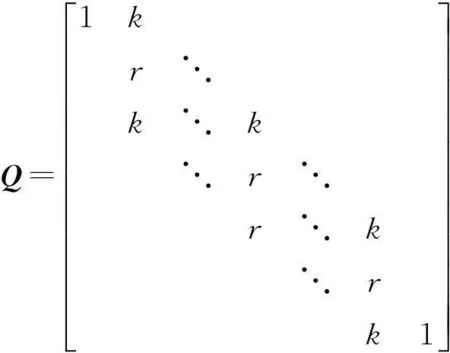
(2)

当x=1时，P,Q为式(2)所示的矩阵，令k=r=1/3,P▽Q可得矩阵每一点的三邻域均值。利用该三邻域均值表示传统二维EMD算法的均值包络曲面，可以稳定迅速地实现二维EMD算法，在速度上比传统算法快2～3个数量级。

2.2.2基于二维快速EMD算法的时频图像降噪算法

高斯白噪声经过EMD获得的每个IMF仍高度

近似服从高斯分布；对噪声图像进行二维EMD分解，获得多个IMF，第1个IMF主要由噪声信号和非常少量的高频图像细节信息组成[11]。利用这一特点，可以对原始时频图像进行自适应的降噪重构。将待分解的时频图像表示为

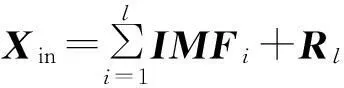
(3)

式中：IMFi∈Rm×n是第i次分解的模态函数分量，Rl∈Rm×n是l次分解后的剩余量。FBEMD降噪算法可描述为：

(1) 初始化：i=1,IMFi=A,R1=A；

(2) 计算均值图像Hi=P×IMFi×QT，从而求得IMFi=Ri-Hi,Ri+1=Hi；

(3) 重复步骤(2)操作，直至获得合适的IMF分量；

(4) 将最后一次的剩余量赋值给Rl.

(5) 重构时频图像矩阵为

(4)

图3表示SNR=-6 dB情况下，FMCW信号的时频图像，其中图3a)为原始PWVD时频图像；图3b)为降噪重构后的PWVD时频图；图3c)为图像二维EMD分量IMF1。经过二维EMD降噪算法，时频图像噪声得到有效抑制，时频集聚性更强，有利于图像特征的提取。

图2　不同LPI雷达信号PWVD时频分布图像Fig.2　PWVD distribution images of different LPI radar signals

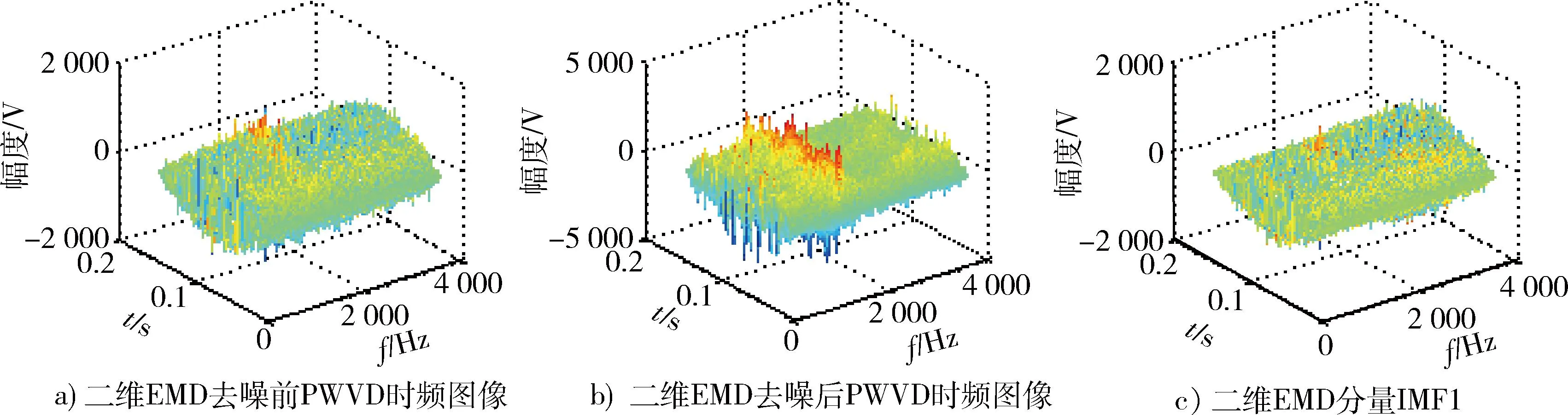
图3　SNR=-6 dB时FMCW信号的时频图像Fig.3　PWVD distribution images of FMCW signals when SNR= -6 dB

1.3时频图像特征提取

1.3.1图像裁剪

时频图像在经过二维EMD分解与重构后，噪声得到有效抑制，但是仍然存在大量冗余信息，首先需要对图像进一步提取和裁剪。图像裁剪步骤如下：

(1) 计算边际频率分布，边际频率分布将信号的瞬时能量表示为频率的函数[3]

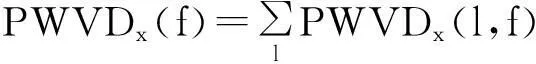
(5)

即对时频图像各频率的时间值相加，储存为列矢量。

(2) 归一化边际频率分布，利用直方图计算获得阈值，确定截取图像的起始和截止频率。

(3) 根据起始频率和截止频率，截取图像，然后将图像调整为固定大小50×200，图4为SNR=-6 dB情况下，FMCW信号截取后的灰度图像。

(4) 将图像转化为10 000×1的列矢量，用于后续的特征提取。

图4　SNR=-6 dB时FMCW信号截取的灰度图像Fig.4　Grayscale image of FMCW signal whenSNR=-6 dB

1.3.2图像特征提取

图像裁剪后，时频图像的冗余信息已经得到很大程度的消除，但是10 000×1的列矢量仍属于高维数据矢量，不适用于实际工程。因此，进一步通过主分量分析(principal component analysis,PCA)和奇异值分解相结合的方式对数据降维[12]，具体过程如下：

(1) 利用一系列训练信号，经过图像预处理后构建训练矩阵X,X的维度为N×P。

(2) 对训练矩阵X进行奇异值分解，得X=UWVH，则U=XVW-1，其中U为N×N酉矩阵，V为P×P酉矩阵，W为非负奇异值构成的N×P矩阵。

(3) 构建投影矩阵A，选取特征矩阵U中低于阈值的特征值置0，阈值选取最大特征值的0.001倍，建立一个非零特征值降序排列的投影矩阵A。

(4) 最后利用公式Y=AHX，获得训练矩阵和测试信号的低维空间投影，完成图像特征的提取。

2仿真实验与结果分析

径向基函数(radial basis function,RBF)神经网络，由于有着结构简单、收敛性好、速度快等优点，目前得到了广泛的使用[13]。本文中，RBF神经网络的输入为测试信号经过图像预处理、特征提取后的低维数据，输出为本实验采用的7种常用的LPI雷达信号。

所有信号载频由900 Hz至1 400 Hz均匀分布,采样频率为10 kHz。BPSK信号采用13位Barker码；FMCW调制带宽为250 Hz和500 Hz，调制周期为20 ms；Frank信号、P1信号、P2信号，设置脉冲压缩比为64，编码周期为1；COSTAS跳频信号，跳频序列设为{3,2,6,4,5,1}×200 Hz，{2,4,8,5,10,9,7,3,6,1}×200 Hz；多时编码信号PT1，相位状态数设为2，步进段数为4。从2 dB到10 dB，每隔2 dB生成10个各种参数的信号，最终生成共280个训练信号。利用本文提出的LPI雷达信号分类识别算法，对这280个训练信号进行处理，利用提取的特征参数训练并保存网络。

文中进行了2组实验，一组为固定信噪比情况下，测试不同信号，研究不同信号测试的识别混淆问题；另一组为固定测试信号种类，改变信噪比，研究不同信噪比情况下信号的识别正确率。

第1组实验，在0 dB信噪比条件下，每种信号按以上信号参数产生100个测试信号，利用本文方法进行实验。实验结果如表1所示，当信号信噪比为0 dB情况下，识别效果良好，平均正确识别率在99%以上。

第2组实验，每种LPI雷达信号，信噪比从-10 dB到10 dB每隔2 dB产生100个测试信号，对测试信号进行分类识别实验。

图5为第2组实验的实验结果，在信噪比SNR>-2 dB时，对于本文采用的7种LPI雷达信号都能有效识别，平均正确识别率达到了93%以上，图像相似度较大的Frank多相码信号和P1多相码信号也可以有效区分；当SNR<-6 dB时，由于PWVD时频分析方法受交叉项影响严重，对于部分LPI雷达信号已经无法有效分析，正确识别率较低。

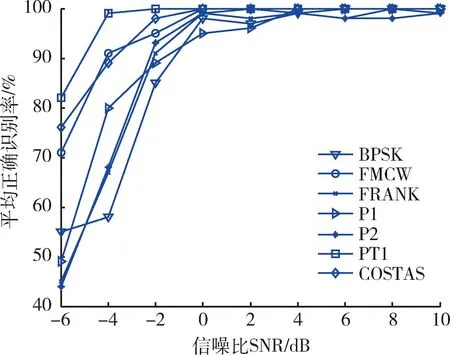
图5　同一LPI信号不同信噪比情况下的识别率Fig.5　Average correct recognition rate of the　　　 same LPI radar signal in different SNR

本文对几种LPI雷达信号时频图像降噪方进行了对比。其中文献[1-2]采用二值化后腐蚀膨胀的算法降噪，文献[3]采用二维高斯低通滤波器降噪。实验过程中，3种降噪算法采用相同的仿真条件，即使用本文采用的信号，时频分析方法和特征提取方法，所得实验结果的不同主要由降噪算法的不同所致。图6表示3种方法在这种实验条件下的平均正确识别率。

在信噪比低于10 dB的情况下，本文方法明显优于其他2种方法。文献[1-2]采用的二值化图像，利用图像腐蚀膨胀降噪，无法获取图像的一些细节信息，如图2中的Frank编码和P1编码的时频图像二值化后，为斜率近似的直线，难以辨识；另一方面二值化图像采用主分量分析法， 无法获取最优主元，也是识别率较低的原因。文献[3]采用二维高斯低通滤波器，一方面频率矩阵值ω1，ω2设置凭经验设置，难以获得适应各种信噪比条件的最优值；另一方面，采用低通滤波器，在去除高频噪声的同时，也使图像丧失了相当一部分高频细节信息，降低信号辨识度。

图6　不同时频图像降噪方法对比Fig.6　Contrast of different time-frequency　　　image de-noising methods

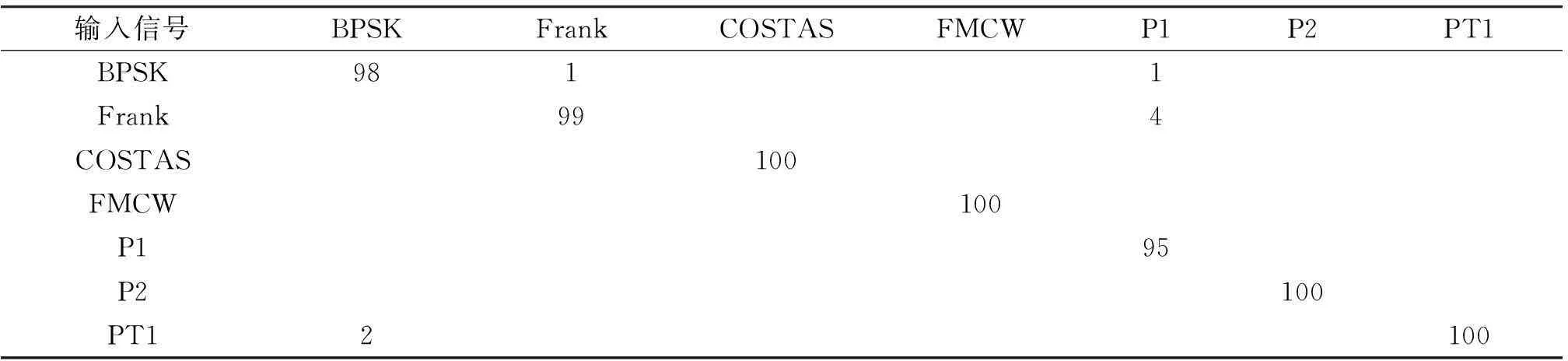
输入信号BPSKFrankCOSTASFMCWP1P2PT1BPSK9811Frank994COSTAS100FMCW100P195P2100PT12100

3结束语

本文针对LPI雷达信号时频图像受噪声干扰严重的问题，使用一种基于二维EMD快速分解的图像降噪方法，有效地降低噪声干扰，使不同LPI雷达信号的时频图像辨识度更佳。处理后的时频图像，经过图像裁剪、特征提取，利用神经网络完成了LPI雷达信号分类识别。在仿真条件相同的条件下，对比了几种LPI时频图像降噪的算法，证明本文方法能够更好地降低时频图像噪声，提高LPI雷达信号分类识别的正确率。但当信噪比低于-4 dB时，识别效果不佳，因为部分信号在较低信噪比下，PWVD时频分析方法受交叉项影响严重，无法获得有效的时频图像，有必要进一步研究对交叉项的抑制。

参考文献：

[1]熊坤来, 罗景青, 吴世龙. 基于时频图像和神经网络的LPI雷达信号调制识别[J]. 弹箭与制导学报, 2012, 31(5): 230-233.

XIONG Kun-lai, LUO Jing-qing, WU Shi-long. Modulation Identification of LPI Radar Signals Based on Time Frequency Image and Neural Network[J]. Journal of Projectiles，Rockets，Missiles and Guidance, 2011, 31(5): 230-233.

[2]白航, 赵拥军, 胡德秀, 等. 基于Choi-Williams时频图像特征的雷达辐射源识别[J]. 数据采集与处理, 2012, 27(4): 480-485.

BAI Hang, ZHAO Yong-jun, HU De-xiu, et al. Radar Emitter Recognition Based on Image Feature of Choi-Williams Time-Frequency Distribution[J]. Journal of Data Acquisition and Processing, 2012, 27(4): 480-485.

[3]ZILBERMAN E R. Autonomous Time-Frequency Cropping and Feature-Extraction Algorithms for Classification of LPI Radar Modulations[R]. Naval Postgraduate School Monterey CA, 2006.

[4]白航, 赵拥军, 胡德秀, 等. 时频图像局部二值模式特征在雷达信号分类识别中的应用[J]. 宇航学报, 2013, 34(1): 139-146.

BAI Hang, ZHAO Yong-jun, HU De-xiu, et al. Radar Signal Recognition Based on the Local Binary Pattern Feature of Time-Frequency Image[J]. Journal of Astronautics, 2013, 34(1): 139-146.

[5]郝士琦, 周建国, 冷蛟锋, 等. 基于时频图像代数特征的雷达信号脉内调制方式分类研究[J]. 电子对抗, 2012(4):22-26.

HAO Shi-qi, ZHOU Jian-guo, LENG Jiao-feng, et al. Research on Classifications of Intra-Pulse Modulation Based on Algebra Characteristics of TFD Images [J]. Electronic Warfare, 2012(4):22-26.

[6]冀贞海, 朱伟强, 赵力, 等. 二维主分量分析的脉内调制识别算法研究[J]. 电光与控制, 2009, 16(11): 33-37.

JI Zhen-hai, ZHU Wei-qiang, ZHAO Li, et al. Intra-Pulse Modulation Recognition Method Based on Two-Dimensional Principal Component Analysis[J]. Electronics Optics and Control, 2009, 16(11): 33-37.

[7]NUNES J C, BOUAOUNE Y, DELECHELLE E, et al. Image Analysis by Bidimensional Empirical Mode Decomposition [J]. Image and Vision Computing, 2003, 21(12):1019-1026.

[8]戴桂平. 基于二维EMD和小波阈值的掌纹图像去噪[J]. 计量学报, 2011, 32(4): 368-372.

DAI Gui-ping. Palm Print Image De-noising Based on 2-D EMD and Wavelet Thresholding[J]. Acta Metrologica Sinica, 2011, 32(4): 368-372.

[9]赵春晖, 任龙涛, 万建. 一种基于二维EMD的图像融合方法[J]. 应用科技, 2009, 36(9): 15-19.

ZHAO Chun-hui, REN Long-tao, WAN Jian. A Method of Image Fusion Based on the Two-Dimensional Empirical Mode Decomposition[J]. Applied Science and Techology, 2009, 36(9): 15-19.

[10]郭珈, 王孝通, 徐晓刚, 等. 基于均值滤波矩阵组的二维信号快速经验模式分解方法[J]. 电子学报, 2013, 40(10): 1980-1983.

GUO Jia, WANG Xiao-tong, XU Xiao-gang, et al. Fast 2D Empirical Mode Decomposition Based on Mean Value Matrix Filter Sets[J]. Acta Electronica Sinica, 2012, 40(10): 1980-1983.

[11]郭耸, 顾国昌, 李常有, 等. 利用 EMD 的自适应图像去噪[J]. 计算机工程与应用, 2013, 49(8): 12-16.

GUO Song, GU Guo-chang, LI Chang-you, et al. Adaptive Image Denoising Based on EMD[J].Computer Engineering and Applications, 2013, 49(8):12-16.

[12]FARGUES M P. Investigation of Feature Dimension Reduction Schemes for Classification Applications[R].Naval Postgraduate School Monterey CA Dept of Electrical and Computer Engineering, 2001.

[13]孙志强，葛哲学．神经网络理论与MATLAB 7实现[M]．北京：电子工业出版社，2005：79-81．

SUN Zhi-qiang, GE Zhe-xue. Neural Network Theory and the Realization of MATLAB7[M]. Beijing: Electronic Industry Press, 2005：79-81.

Radar Signal Classification Based on Two-Dimensional Empirical Mode Decomposition of Time-Frequency Images

ZHANG Fan1, DIAO Ming1, YANG Cheng-zhi1，2

(1. Harbin Engineering University, College of Communication and Information Technology,Heilongjiang Harbin 150001, China 2. Aviation University of Air Force, Department of Communication Counter,Jilin Changchun 130022, China)

Abstract:To classify low probability of intercept (LPI) radar signals correctly, a novel method based on two-dimensional fast empirical mode decomposition (FBEMD) algorithm is proposed. The method is used to reduce the time-frequency image noise. Firstly, time-frequency images are obtained by using PWVD distribution. Intercept image part with signal information and extract feature vector by principal component analysis (PCA). Finally, the radial basis function(RBF) neural network is used to automatically classify LPI radar signals. Simulation results show that the method is effective at low signal noise ratio(SNR). By using FBEMD noise reduction algorithm, the average correct recognition rate can reach 93% when SNR is -2 dB.

Key words:low probability of intercept(LPI) radar signals; time-frequency distribution; two-dimensional empirical mode decomposition(EMD); principal component analysis

中图分类号：TN957.52；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-05-0172-06

doi:10.3969/j.issn.1009-086x.2015.05.028

通信地址：150001黑龙江省哈尔滨市南岗区哈尔滨工程大学信息与通信工程系E-mail：zhangfan8908@gmail.com

作者简介：张帆(1989-)，男，山东日照人。硕士生，研究方向为雷达信号处理。

*收稿日期：2014-06-05；修回日期：2014-08-28