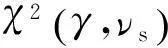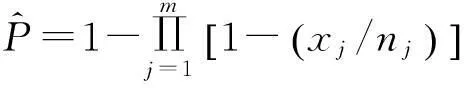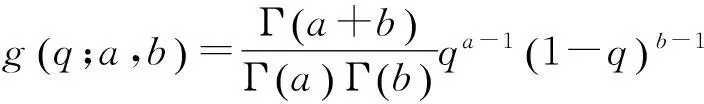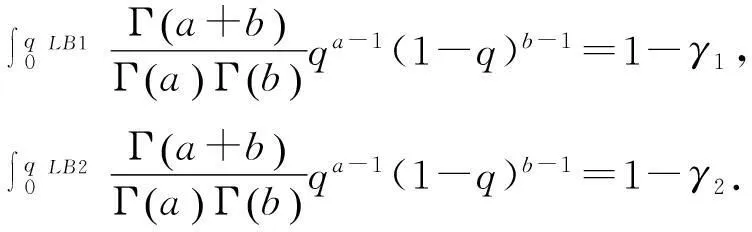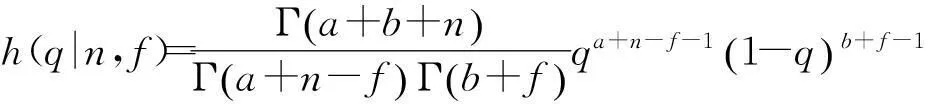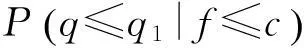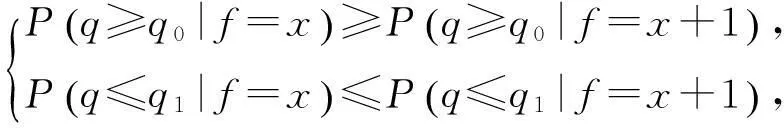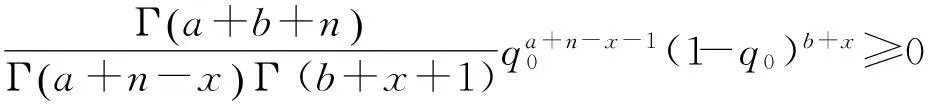利用分系统数据制定整机测试性验证试验方案*1



利用分系统数据制定整机测试性验证试验方案*1

王敏，杨江平，卢雷，王永攀

(空军预警学院，湖北 武汉430019)

摘要：现有利用研制阶段试验数据制定测试性验证试验方案的方法都需要装备整机系统测试性先验信息，这对仅有分系统试验信息的大型复杂装备难以适用。针对这一问题，以故障检测率为验证指标，提出利用研制阶段分系统试验数据制定整机测试性验证试验方案的新方法。首先，利用分系统试验数据计算整机系统故障检测率置信下限，然后利用两点分位数方法确定整机故障检测率的先验分布参数，在此基础上根据贝叶斯最大后验风险准则确定了新的测试性验证试验方案。实例对比分析表明，与传统试验方案相比，新方案可明显降低试验故障样本量。

关键词：测试性；验证试验方案；分系统试验信息；故障样本量；故障检测率；贝叶斯方法

0引言

在装备投入使用前，为了判定是否达到了规定的测试性要求，需进行测试性验证试验。测试性验证试验应首先确定试验故障样本量及允许的最大故障检测或隔离失败数，即测试性验证试验方案[1]。

现有测试性验证试验方案一般依据一些军用标准来制定[2-3]。文献[4]对比分析了二项分布模型、泊松分布模型、正态分布模型以及多项分布模型的优缺点和适用性，得出二项分布模型和泊松分布模型在确定测试性验证试验方案上具有明显的优势。文献[5]通过对二项分布函数单调性的讨论，提出了求解二项分布函数联立不等式的精确算法，可迅速准确地获得测试性验证的抽样方案。文献[6-7]分析了国内外现有军用标准中给出的测试性验证方法，总结出现有方法存在普遍适用性缺乏、可操作性差等不足之处，提出应该制定测试性验证专用标准。以上标准与方法中关于验证试验方案的确定是在对装备测试性水平完全未知的情况下确定的，往往具有试验样本量大、试验周期长、费用高等缺点，在工程上难以实现。为此，国内外学者开始关注如何利用验证试验前的先验信息来制定测试性验证试验方案，进而减少试验故障样本量，节省试验费用。文献[8-9]将研制阶段的试验数据进行折合，得到验证试验前故障检测率(fault detection rate, FDR)的信仰(fiducial)分布，依据此分布制定了FDR的验证试验方案。由于利用了研制阶段的试验数据，得到的试验方案相比于二项分布法，样本量减少效果明显，但没有考虑研制过程中多阶段的试验数据来自不同总体的特点。文献[10]运用证据理论方法，建立了基于融合不同种类研制信息(测试性试验数据、测试性预计结果和专家经验)的测试性验证试验方案。文献[11]提出利用研制阶段试验数据和专家信息制定测试性验证试验方案的贝叶斯方法。该方法首先利用研制阶段试验数据建立了产品的FDR增长模型，以此描述FDR在研制阶段的变化趋势，然后利用专家信息确定模型中的超参数，进而得到FDR的验前分布，最后依据贝叶斯最大后验风险准则制定了新的测试性验证试验方案。

上述研究利用的先验信息都是整机系统自身的历史试验数据，而对于设备量大或体积庞大的装备，如大型复杂电子装备，由于系统复杂，试验组织困难，试验费用高昂，研制过程中整机系统自身的试验较少甚至没有，因此，上述研究在制定大型复杂装备测试性验证试验方案上适用性不强。在实际工程中，为保证整机系统的测试性水平，构成整机系统的分系统通常会有较多的试验数据，通过这些数据可以确定整机系统的测试性先验水平。基于文献[12]，根据将分系统试验数据融合到可靠性验证中的思想，本文以整机系统故障检测率FDR为验证指标，讨论了二项分布下，利用分系统试验数据制定整机系统测试性验证试验方案的新方法。本文方法适用于整机测试性先验信息缺乏的情况，依据本文方法确定的测试性验证试验方案，可有效减少故障样本量，节省试验费用。

1FDR一次抽样试验方案

FDR的验证试验可以看成是成败型试验。典型的FDR一次抽样试验方案的思路是：随机抽取n个故障样本进行试验，其中有f次没检测到故障(检测失败)。规定一个正整数c，如果f≤c则认为FDR合格，判定接收；如果f>c则认为不合格，判定拒收。试验方案简记为(n，c)。

设装备整机系统的FDR为q，则在n次试验中，出现f次失败的概率为

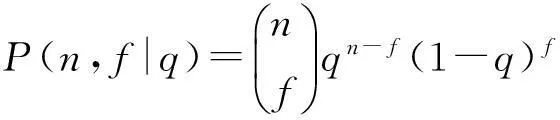
(1)

产品被接收的概率，即f≤c的概率为

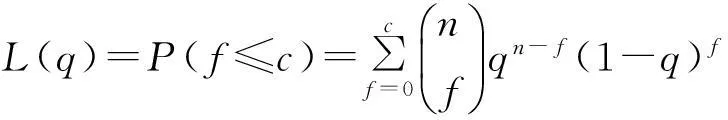
(2)

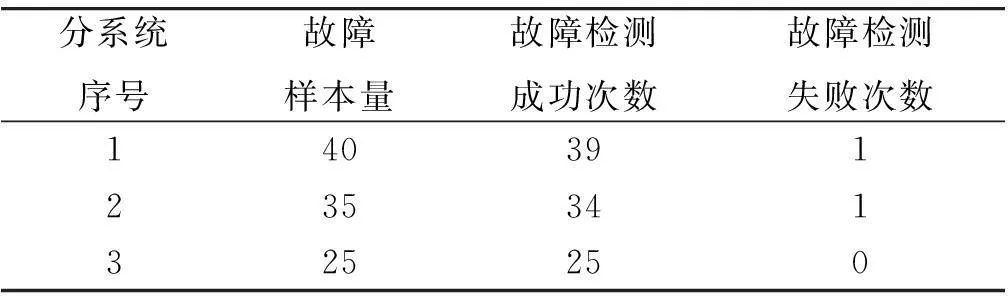
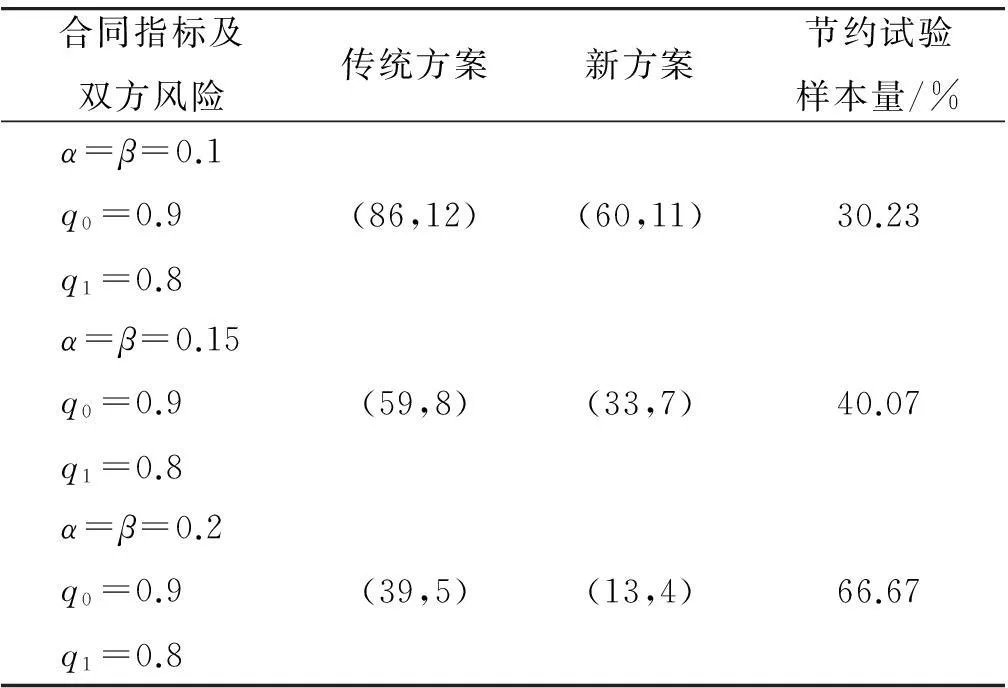
装备在设计之初，使用方和生产方协商确定FDR的设计要求值q0(规定值)和最低可接受值q1，且q1

(3)

对于FDR要求较高的装备，若双方要求风险较低，则依据式(3)确定的故障样本量很大。例如，对于大型相控阵雷达，如果规定q0=0.95,q1=0.90，α=β=0.05，则可确定试验方案为(298,21)。由于故障注入试验的破坏性，在装备中注入大量的故障是不现实的。因此，上述试验方案在工程中很难以实现。

2利用分系统数据制定整机测试性验证试验方案的方法

2.1方法流程

新方法的流程如图1所示：首先利用分系统试验数据计算整机系统FDR置信下限，然后采用两点分位数方法确定整机系统FDR的Beta先验分布参数，最后在给定α，β，q0，q1情况下，依据贝叶斯最大后验风险准则制定整机系统FDR的验证试验方案。

图1　方法流程图Fig.1　Flow chart of the method

2.2计算整机故障检测率置信下限

考虑由m个分系统组成的串联整机系统，设各分系统故障发生相互独立，第j(j=1,2,…,m)个分系统在进行测试性验证试验时，注入故障样本量为nj，其中有xj次故障检测失败。利用近似最优法求取整机系统FDR的置信下限[10]，计算公式如下：

当νs<3时，

(4)

(5)

当νs≥3时，

(6)

(7)

(8)

νs=4ms/Δ，

(9)

(10)

(11)

2.3确定整机故障检测率先验分布

系统FDR的先验分布类型，国内外文献大多选取Beta(a，b)分布，其密度函数可表示为

(12)

确定整机系统FDR的先验分布参数，可给定2个不同的置信水平，由式(4)，(5)或式(6)，(7)分别求出其对应的单侧置信下限，进而利用两点分位数方法确定先验分布的参数，如下所示：

(13)

用Matlab软件编制程序可求解出参数a和b,进而得到整机FDR的先验分布。

2.4确定整机系统测试性验证试验方案

在获得整机FDR先验分布后，即可制定相应测试性验证试验方案。假设使用方和生产方协商确定的试验方案为(n，c)，现场验证试验结果为(n，f)，f表示故障检测失败次数，则整机故障检测率FDR的后验分布为

(14)

即q的后验分布为Beta(a+n-f，b+f)分布。

根据式(14)可证明如下不等式组成立：

(15)

上述不等式组中2个不等式证明类似，下面证明第1个不等式：

maxP(q≤q1|f≤c)=P(q≤q1|f=c).

(16)

(17)

若规定使用方风险为β，生产方风险为α，则可由下列不等式组制定新的试验方案(n，c)。

(18)

3实例分析

某电子设备由3个分系统串联而成，在研制过程中分别对各分系统进行测试性试验。各分系统试验数据见表1。

表1　各分系统试验数据

对表1中分系统试验数据进行折合，可得出整机故障检测率的Beta先验分布参数a=25，b=2。在求得先验分布后，就可制定整机可靠度新试验方案。

为了对比分析传统一次抽样试验方案和新试验方案的优劣，选取3组不同的合同指标及风险组合，对比分析结果见表2。

表2　传统试验方案和新试验方案的结果对比

由表2的对比分析结果可以看出，整机故障检测率新试验方案由于考虑了分系统的试验信息，相比传统试验方案具有以下优点：

(1) 在双方风险相同的情况下，新试验方案可明显减少试验样本。例如在第1种组合情况下，试验故障样本量可节约30.23%。

(2) 由于需注入的故障样本量少，新试验方案可操作性更强。

4结束语

本文方法可以充分利用装备研制阶段分系统的测试性试验信息，对于整机系统测试性先验信息缺乏的情况尤为适用。

采用本文方法制定的整机测试性验证试验方案较传统一次抽样方案试验所需故障样本量大为降低，可节约试验经费。

参考文献：

[1]田仲,石君友.系统测试性设计分析与验证[M].北京:北京航空航天大学出版社,2003.

TIAN Zhong, SHI Jun-you. Design, Analysis and Demonstration of System Testability [M]. Beijing: Beihang University Press, 2003.

[2]Department of Defense Washington D C. MIL- STD-471A: Maintainability Verification/Demonstration/Evaluation [S]. U. S Government Printing Office, 1973.

[3]国防科学技术工业委员会.GJB 2072-94 维修性试验与评定[S].北京:中国标准出版社,1994.

National Science and Technology Industrial Committee. GJB 2072-94 Maintainability Test and Evaluation[S].Beijing: Standards Press of China.1994.

[4]田仲, 石君友.现有测试性验证方法分析与建议[J].质量与可靠性,2006,21(2):47-51.

TIAN Zhong, SHI Jun-you Analysis and Advice for the Existing Testability Demonstration Methods [J].Quality and Reliability, 2006, 21(2):47-51.

[5]徐忠伟,周玉芬,徐松涛,等.测试性验证中的精确算法及应用[J].航空学报,2000,21(1):67-69.

XU Zhong-wei, ZHOU Yu-fen, XU Song-tao,et al. Accurate Algorithm of Sampling Plan and Its Application in Testability Demonstration[J].Acta Aeronautica et Astronautica Sinica, 2000, 21(2): 67-69.

[6]周玉芬,徐松涛,高锡俊,等.测试性验证的理论和方法[J].电子产品可靠性与环境试验,1998,19(2):10-15.

ZHOU Yu-fen, XU Song-tao, GAO Xi-jun, et al.Research on Theory and Method of Testbility Demonstration Test [J].Electronic Product Reliability and Environment Testing, 1998, 19(2):10-15.

[7]石君友,纪超,李海伟.测试性验证技术与应用现状分析[J].测控技术,2012,31(5):29-32.

SHI Jun-you，JI Chao，LI Hai-wei. Analysis of Testability Verification Technology and Application Status [J].Measurement and Control Technology, 2012, 31(5):29-32.

[8]李天梅，邱静，刘冠军.利用研制阶段试验数据制定测试验证试验方案新方法[J].机械工程学报,2009,45(8):52-57.

LI Tian-mei, QIU Jing, LIU Guan-jun.New Methodology for Determining Testability Integrated Teat Scheme with Test Data in the Development Stages [J].Journal of Mechanical Engineering, 2009, 45(8): 52-57.

[9]李天梅，邱静，刘冠军. 基于Bayes变动统计理论的测试性外场统计验证方法[J]. 航空学报,2010,31(2):335-341.

LI Tian-mei, QIU Jing, LIU Guan-jun.Research on Testability Field Statistics Verification Based on Bayes Inference Theory of Dynamic Population[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2):335-341.

[10]常春贺,杨江平,曹鹏举.基于研制信息的测试性验证试验方案研究[J].航空学报,2012,33(11): 2057-2064.

CHANG Chun-he, YANG Jiang-ping, CAO Peng-ju. Study on the Scheme of Testability Demonstration Test Based on Development Information[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2057-2064.

[11]雷华军,秦开宇.确定测试性验证试验方案的贝叶斯方法[J].系统工程与电子技术,2012,34(12):2612-2616.

LEI Hua-jun, QIN Kai-yu. Bayesian Method for Determination of Testability Demonstration Test Scheme [J]. Systems Engineering and Electronic, 2012, 34(12):2612-2616.

[12]Nancy R Mann. Approximately Optimum Confidence Bounds on Series and Parallel-System Reliability for Systems with Binomial Subsystem Data [J].IEEE Transactions on Reliability, 1974, 23(5): 295-304.

Determining Testability Demonstration Test Scheme with Subsystem Data

WANG Min，YANG Jiang-ping，LU Lei，WANG Yong-pan

(Air Force Early Warning Academy,Hubei Wuhan 430019, China)

Abstract:Existing method using development stage test data to determine testability demonstration test scheme needs whole system prior information, and is difficult to apply when only subsystem data are available. To solve this problem, taking the system failure detection rate as a target, a new method is presented to make full use of the subsystem test data. Firstly, the subsystem test data is used to calculate the confidence bound of system failure detection rate. Then, the two percentile method is applied to determine the prior distribution of system failure detection rate. Finally, a new testability demonstration test scheme is defined according to the Bayesian maximum posterior risk rule. Compared with the classical test scheme, the new scheme can obviously reduce the failure sample size.

Key words:testability; demonstration test scheme; subsystem test data; fault sample size; fault detection rate; Bayesian method

中图分类号：TJ06

文献标志码：A

文章编号：1009-086X(2015)-05-0213-05

doi:10.3969/j.issn.1009-086x.2015.05.034

通信地址：430019湖北省武汉市黄浦大街288号研究生管理大队20队E-mail：lyanmin87@163.com

作者简介：王敏(1987-)，女，山东莱芜人。博士生，主要研究方向为预警装备管理与保障。

*收稿日期：2014-06-18；修回日期：2014-08-23