大型导弹发射装置风载荷响应分析*1
2015-03-09杨铮,岳瑞华,徐中英
大型导弹发射装置风载荷响应分析*1
杨铮,岳瑞华,徐中英
(第二炮兵工程大学,陕西 西安710025)
摘要:风载荷是导弹发射装置结构设计中的重要设计载荷,大型导弹由于长度较大、具有大长细比,因此其发射装置在起竖后受到风载荷的影响较大。分析了自然风的组成和特性,应用随机振动理论分别研究了平均风和脉动风对导弹发射装置起竖后的影响作用,建立数学模型并用Matlab软件模拟仿真了发射装置产生的位移响应,为该型导弹发射装置的设计提供了一定的理论依据。
关键词:发射装置;风载荷;位移响应;Matlab
0引言
大型导弹长度较大,具有大长细比,故其发射装置也具有大长度,大长细比。由于导弹在发射前需要进行战前检查、导入数据等,因此发射装置可能较长时间地竖立在发射场坪上,受到外界环境因素的干扰,风载荷是其中最主要的干扰因素[1]。风载荷在导弹上会产生较大的定常或非定常载荷,引起发射装置的振动,进而对弹上仪器设备的正常工作和弹体控制系统的调整带来误差影响。因此,分析研究发射装置起竖后由于风载荷的作用产生的位移响应,对保证弹上仪器设备处于正常工作状态、确保发射安全具有重要意义。
1风载荷的组成特性
风对结构的作用主要有2个方面,即顺风向和横风向,通常对于非圆截面,顺风向风振响应占据主要地位[2]。本文主要考虑顺风向风力对发射装置的影响。
根据大量文献可以知道,在风的顺风向过程曲线中,主要包括2种成分[3]:一种是长周期部分,时间通常持续在10 min以上,这部分称作平均风。由于平均风的周期远远大于弹体的自振周期,因此其相当于静力作用在弹体上;一种是短周期部分,时间通常只有几秒钟左右甚至更短,这部分称作脉动风。脉动风是由于风的不规则性引起的,它的速度、方向是随机变化的,因而其相当于动力作用在弹体上,这将引起弹体结构的随机振动。
理论上研究风载荷作用下位移响应的方法主要有2种方法:一是频域法,应用随机振动理论,建立输入的风荷载功率谱与输出的位移响应之间在频域内的关系;二是时域法,将风荷载模拟成时间的函数,然后求解运动微分方程。为了便于理解、减小计算量,本文采用频域法进行分析计算。
2导弹发射装置位移响应
2.1导弹发射装置在平均风载荷作用下位移响应
由建筑结构荷载规范可知,作用在结构上任一处的平均风压或风载荷ωz与结构体型系数、风压高度变化系数有关。在一定高度范围内作用于发射装置表面单位面积上任意高度处的风压为[3]
ωz=μs(z)μz(z)ω0,
(1)
式中:ω0为发射所在地的基本风压(kN/m2),这里假设发射地点在西安,则ω0=0.35 kN/m2;μs为风载荷体型系数,与发射筒的体型和尺寸大小有关,由于发射筒横截面是圆形的,根据该型导弹尺寸大小取μs=1.057;μz为风压高度变化系数,它充分考虑了地面粗糙度及风速随高度变化的影响。
导弹发射装置在平均风载荷作用下的位移响应可用结构静力学来分析,也就是在计算出平均风载荷后分析弹体的内力、变形等。一般情况下可以用虚功原理来进行计算,但计算过程较为繁琐,在实际运用中要解决诸多问题。因此本文在满足精度要求的前提下,采用一种近似的方法做简化计算[4-5]。
结构任意高度上的静力位移为

(2)

对于位移响应来讲,第1阶振型起着决定性作用,则式(2)可写成:

(3)
对于等截面结构,质量可看作是沿高度的均匀分布,则
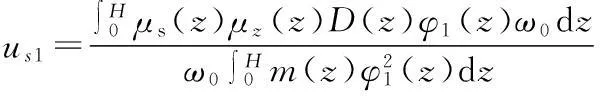
(4)
式中:m(z)为发射装置单位长度上的质量。
2.2导弹发射装置结构在脉动风载荷作用下响应
脉动风载荷属于随机载荷,发射装置在脉动风载荷作用下的响应需用随机振动理论求解[6-7]。具有大细长比的导弹发射装置可以看作是高耸结构,属于无限自由度体系,现将发射装置作为一维结构来处理,连续化弹性振动方程为[8]
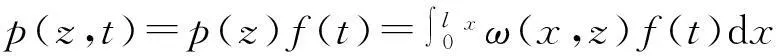
(5)
式中:c(z)为单位高度上的阻尼;I(z)为单位高度上的惯性矩;p(z)为单位高度上的风力;f(t)为时间函数,最大值为1;ω(x,z)为高度z处的风压。
用振型分解法求解,位移按振型展开为
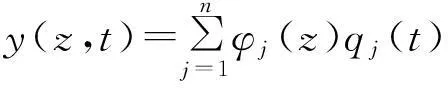
(6)
式中:φj(z)为第j振型在高度z处的值;qj为第j振型的广义坐标。
当输入力按振型乘权函数m(z)展开式,得到:

(7)
由振型正交性,得到:
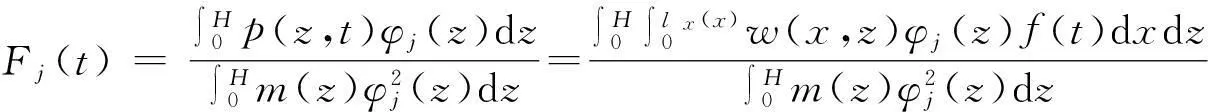
(8)
设阻尼为比例阻尼并且各振型阻尼系数之间相互没有影响,各振型阻尼系数可用各振型阻尼比ξi表示,则可得到广义坐标方程为

(9)
用随机振动理论解此方程,得到位移响应的功率谱密度函数:
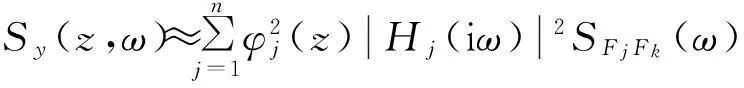
(10)

(11)
式中:Sj(ω)为Davenport功率谱;p0(z)为不计空间相关性时高度z处的脉动风压;ρxz为上下左右相关性函数。
将位移响应功率谱密度函数在频域内积分,再利用平方总和开方法即可得到位移响应根方差为[9]
μz(z)μf(z′)μs(z′)μz(z′)ρxz(x,x′,z,z′,ω)·
φj(z)φj(z′)dxdx′dzdz′dω]0.5,
(12)
式中:μf(z)为脉动系数;μs(z)为风载荷体型系数;μz(z)风压高度变化系数;μ为保证系数(峰因子);Hj(iω)为第j振型的传递函数。
3算法分析
本文采用Matlab软件对该型导弹发射装置进行分析,通过编写M函数,建立起风载荷和导弹发射装置的数学模型,进而对导弹待发射状态下受风载荷的位移响应进行仿真研究[10-11]。为计算简便,定义该导弹发射装置为圆柱体,高度为20 m,直径为1.4 m;发射装置和导弹均为普通钢,密度为7 800 kg/m3,泊松比为0.3,弹性模量为2e11 N/m2,整个发射装置是由钢材组成的实体结构[12]。
利用Matlab进行仿真,得到导弹发射装置在风载荷作用下各节点的位移响应,如图1~5所示。
由得到的数据可知,由于风载荷的作用,导弹发射装置顶部节点的位移响应比中部节点的位移响应要大,从而导致导弹中心线在起飞之前会产生一个垂直误差角,所谓的垂直误差角即发射装置与理论铅垂线之间的夹角,如表1所示。当角度达到一定的程度时就会严重影响到了导弹的发射安全和命中精度。由此可见,该型导弹的发射受到自然条件的制约,不能做到全天候发射,选择发射窗口必须考虑自然环境的影响。
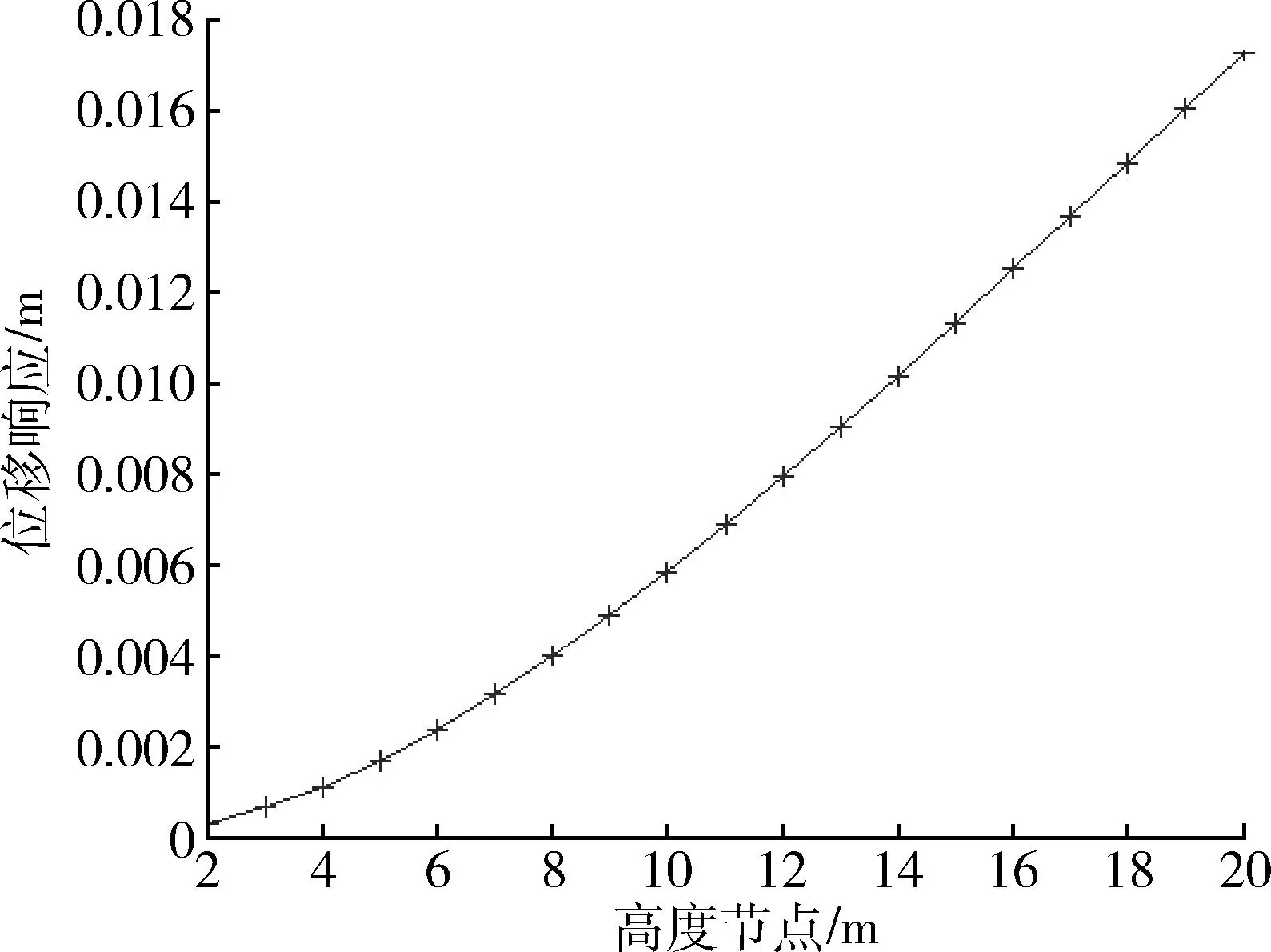
图1 风速10 m/s发射装置的位移响应Fig.1 Displacement response of the launcher when the wind speed is 10 m/s
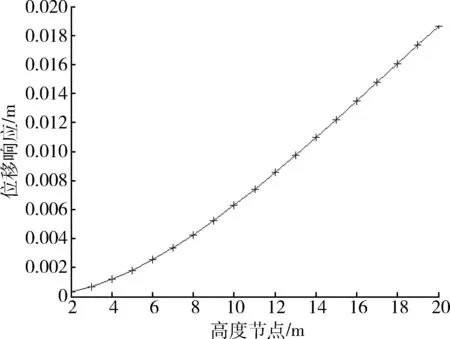
图2 风速15 m/s发射装置的位移响应Fig.2 Displacement response of the launcher when the wind speed is 15 m/s

图3 风速18 m/s发射装置的位移响应Fig.3 Displacement response of the launcher when the wind speed is 10 m/s
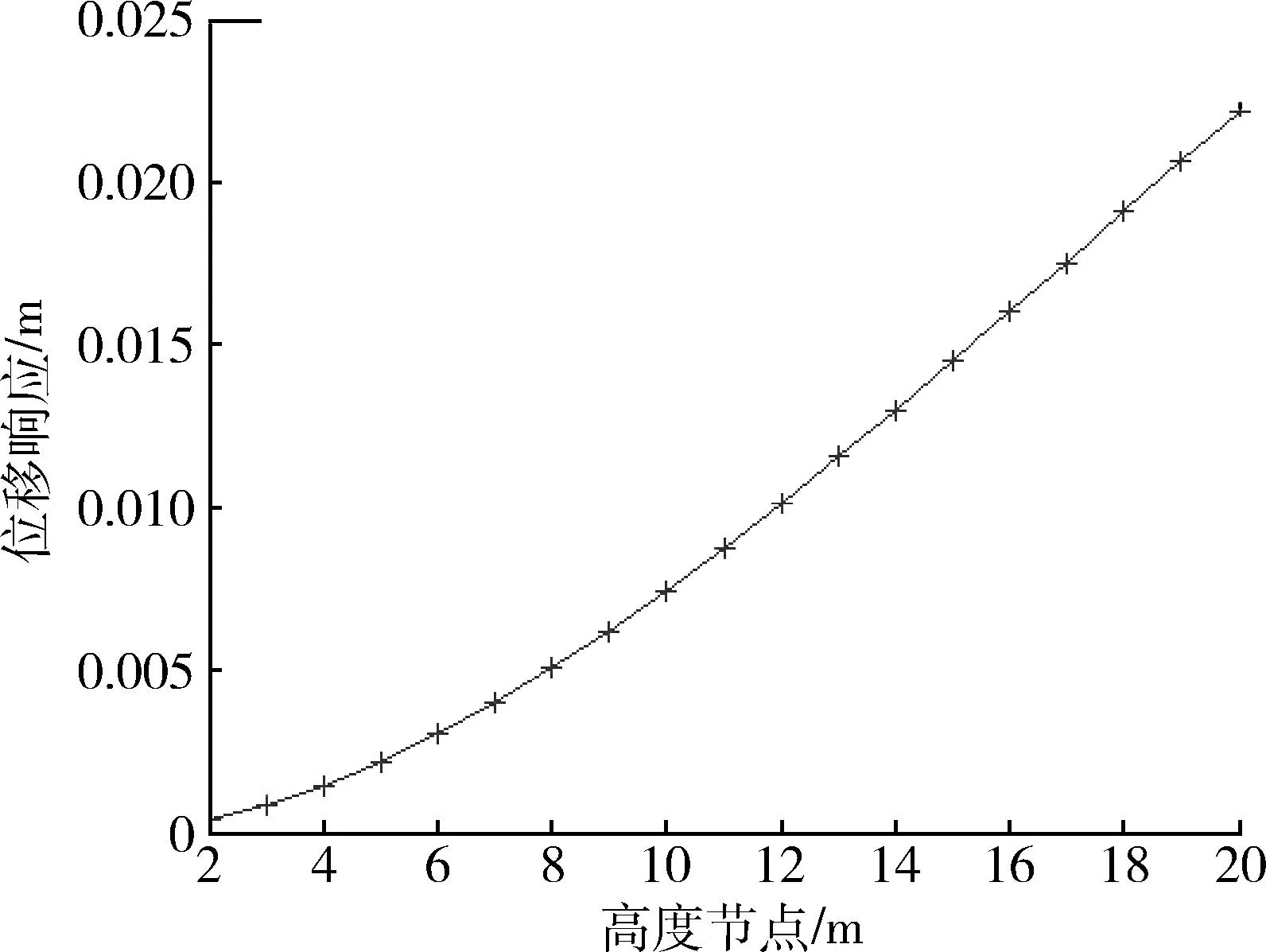
图4 风速22.5m/s发射装置的位移响应Fig.4 Displacement response of the launcher when the wind speed is 22.5 m/s
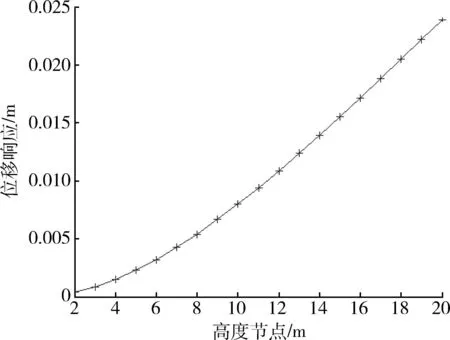
图5 风速25 m/s发射装置的位移响应Fig.5 Displacement response of the launcher when the wind speed is 25 m/s

风速/(m·s-1)发射装置顶部位移响应/m发射装置垂直误差角/(°)100.01720.0653150.01860.0705180.01980.075122.50.02220.0842250.02380.0905
4结束语
本文对风载荷进行了分析,将风载荷分为平均风和脉动风,分别研究了大长细比导弹发射装置起竖后在两者作用下的位移响应,并进行仿真分析研究,得出结论为:①导弹发射装置的设计定型必须要满足在一定风载荷环境中的使用要求;②该型导弹全天候全时段的作战能力受到自然条件,尤其是风载荷的制约,必须考虑自然环境的影响才能确保导弹发射的安全性和命中精度。
参考文献:
[1]谢建, 胡一全, 田桂. 导弹起竖过程中风载荷影响研究[J]. 战术导弹技术, 2009(6): 15-18.
XIE Jian, HU Yi-quan, TIAN Gui. Study of Wind Load Effects in the Process of Missile Erecting[J]. Tactical Missile Technology, 2009(6): 15-18.
[2]马宇山, 金涛. 基于 ANSYS 的塔设备地震与风载分析[J]. 制造业自动化, 2010 (1): 1-5.
MA Yu-shan, JIN Tao. Seismic and Wind Load Analysis of the Tower Equipment with ANSYS [J]. Manufacturing Automation, 2010 (1):1-5.
[3]张相庭.结构风压和风振计算[M].上海:同济大学出版社,1985.
ZHANG Xiang-ting. The Structure of Wind Pressure and Wind Vibration Calculation [M]. Shanghai: Tongji University Press, 1985.
[4]陶贵明, 曾兴志, 王俊红. 导弹发射动力学分析[J]. 电脑与信息技术, 2012, 20(1): 29-32.
TAO Gui-ming, ZENG Xing-zhi, WANG Jun-hong. Analysis of Launching Dynamic of Guided Missile [J]. Computer and Information Technology, 2012, 20(1): 29-32.
[5]钟音亮, 杨茂, 陈凤明. 垂直发射飞行器地面风荷载响应[J]. 科学技术与工程, 2010,10 (24): 6109-6112.
ZHONG Yin-liang, YANG Mao, CHEN Feng-ming. The Response of Vertical Launch Vehicle to Ground Wind [J]. Science Technology and Engineering, 2010,10 (24): 6109-6112.
[6]VICKERY B J,BASU R I.Across-Wind Vibrations of Structures of Circular Cross-Section[J].Journal of Wind Engineering and Industrial Aerodynamics,1983,12(1):49-73.
[7]Donald A Buell,George B McCullough,William J Steinmetz. A Wind Tunnel-Investigation of Ground-Wind Loads on Axisymmetric Lauch Vehicles[R].NASA TND-1893,United States:National Aeronautics and Space Administration,1963.
[8]马学坤, 曹宗胜, 邹振祝. 航天器发射塔风振响应分析[J]. 国防交通工程与技术, 2006, 3(4): 27-30.
MA Xue-kun, CAO Zong-sheng, ZOU Zhen-zhu. Wind Induced Response Analysis of Spacecraft Launching Tower[J]. Traffic Engineering And Technology for National Defence, 2006, 3(4): 27-30.
[9]李哲, 安军, 万小朋. 运载火箭地面风载荷响应特性分析[J]. 航空工程进展, 2013, 4(2): 199-203.
LI Zhe, AN Jun, WAN Xiao-peng. Response of Launch Vehicle under Ground Wind Load [J]. Advances in Aeronautical Science and Engineering, 2013, 4(2): 199-203.
[10]高会生,李新叶,胡智奇.MATLAB原理与工程应用[M].北京:电子工业出版社,2002.
GAO Hui-sheng, LI Xin-ye, HU Zhi-qi. Principle and Engineering Application of the MATLAB [M]. Beijing: Electronic Industry Press, 2002.
[11]石国春.关于序列二次规划(SQP)算法求解非线性规划问题的研究[D].兰州:兰州大学,2009.
SHI Guo-chun. Research of the Sequential Quadratic Programming (SQP) Algorithm to Solve the Nonlinear Programming Problem [D].Lanzhou: Lanzhou University, 2009.
[12]唐卫华.某型导弹发射装置的多状态动力学研究[D].西安:西北工业大学,2007.
TANG Wei-hua. Research of Some States Dynamics for A Missile Launching System [D]. Xi′an: Northwestern Polytechnical University, 2007.
Analysis of Wind load Effects on Some Large Missile Launching Device
YANG Zheng,YUE Rui-hua,XU Zhong-ying
(The Second Artillery Engineering University,Shaanxi Xi’an710025,China)
Abstract:Wind load is very important in the structure design of missile launching device. Some large missile has large length and large slenderness ratio, so the missile launching device is under the serious influence of wind load when it is erected. The composition and properties of the wind load are analyzed and the impact by the average wind and fluctuating wind on missile launching device is studied with the random vibration theory. Matlab software is used to establish the mathematical model and simulate the displacement response produced by the launcher, so this research provides useful information for the design of the missile launching device.
Key words:launcher; wind load; displacement response; Matlab
中图分类号:TJ768;TP391.9
文献标志码:A
文章编号:1009-086X(2015)-05-0218-05
doi:10.3969/j.issn.1009-086x.2015.05.035
通信地址:430000湖北省武汉市江岸区工农兵路145号40栋3单元401E-mail:552509731@qq.com
作者简介:杨铮(1989-),男,河北衡水人。硕士生,研究方向为控制科学与工程。
*收稿日期:2014-06-18;修回日期:2014-08-22
